人教版数学 七年级下册5.1.2 垂线课件(共23张PPT)
文档属性
| 名称 | 人教版数学 七年级下册5.1.2 垂线课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 540.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
5.1.2垂线
【学习目标】
1.理解垂线段的概念、“垂线段最短”的性质;
2.理解点到直线的距离的意义并会度量点到直线的距离。
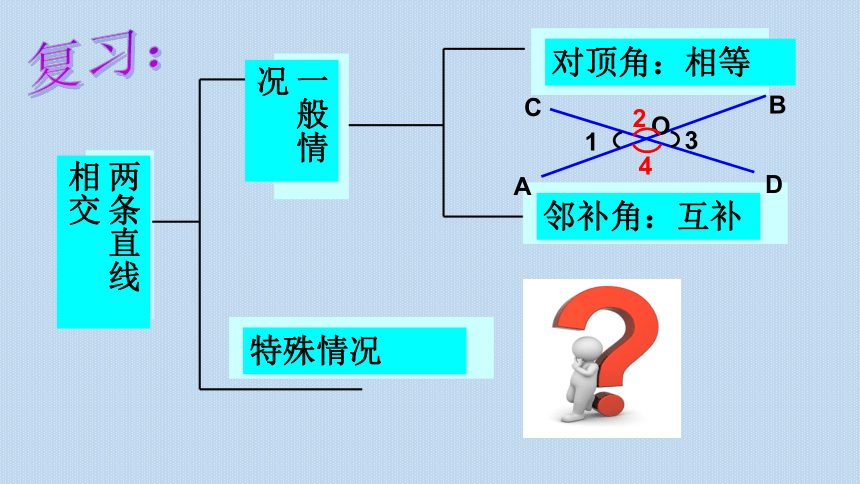
两条直线相交
一般情况
对顶角:相等
邻补角:互补
B
A
C
D
O
1
2
3
4
特殊情况
复习:
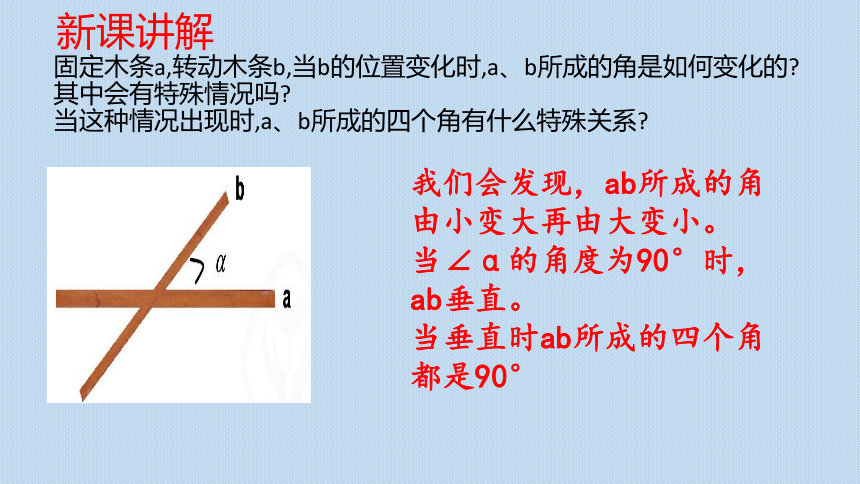
固定木条a,转动木条b,当b的位置变化时,a、b所成的角是如何变化的
其中会有特殊情况吗
当这种情况出现时,a、b所成的四个角有什么特殊关系
我们会发现,ab所成的角由小变大再由大变小。
当∠α的角度为90°时,ab垂直。
当垂直时ab所成的四个角都是90°
新课讲解
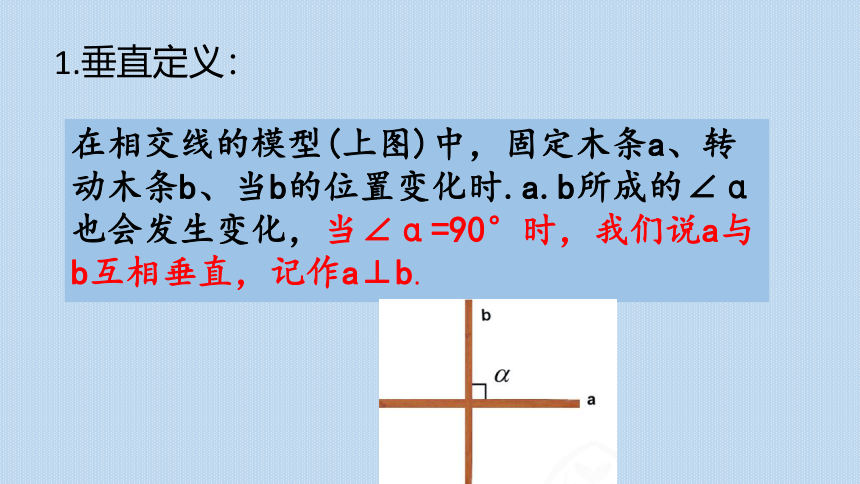
1.垂直定义:
在相交线的模型(上图)中,固定木条a、转动木条b、当b的位置变化时.a.b所成的∠α也会发生变化,当∠α=90°时,我们说a与b互相垂直,记作a⊥b.
2.分清“互相垂直”与“垂线”的区别与联系:
“互相垂直”指两条直线的位置关系;
“垂线”是指其中一条直线对另一条直线的命名。
3.垂直的表示法:
“直线AB垂直于直线CD,垂足为O”,记为AB⊥CD,垂足为O,AB是CD的垂线,CD也是AB的垂线,他们互为垂线!
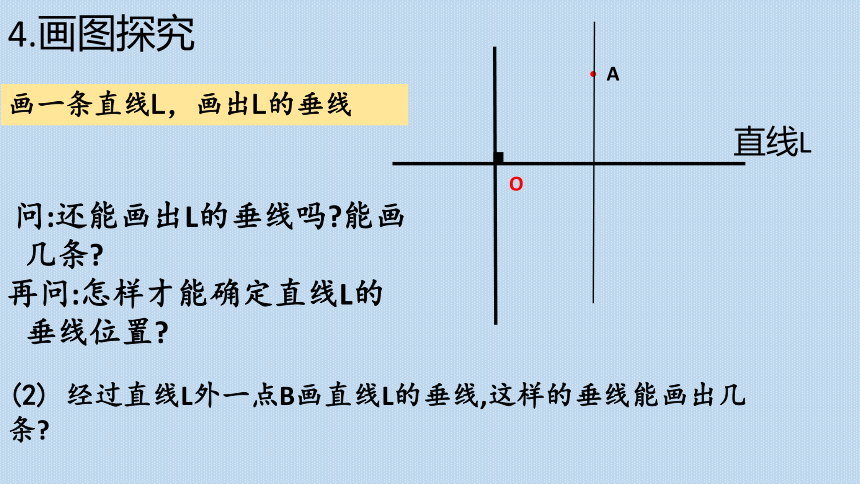
画一条直线L,画出L的垂线
问:还能画出L的垂线吗 能画几条
再问:怎样才能确定直线L的垂线位置
4.画图探究
直线L
■
O
(2) 经过直线L外一点B画直线L的垂线,这样的垂线能画出几条
A
·
经过直线上或者是外一点有且只有一条直线与已知直线垂直.
垂线性质1:过一点有且只有一条直线与已知直线垂直.
5.问题:要把河中的水引到农田P处,如何挖渠能使渠道最短
·p
提示,上学期我们曾经学过什么最短的知识,还记得吗
两点间线段最短.
如果把渠道看成直线L,连接直线L外一点P与直线L上各点的线段中,哪一条最短
L
如图所示,PC最短!连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.(PC的长)
判断以下两条直线是否垂直:
①两条直线相交所成的四个角中有一个是直角;
②两条直线相交所成的四个角相等;
③两条直线相交,有一组邻补角相等;
④两条直线相交,对顶角互补.
√
√
√
√
性质
点到直线的距离:
直线外一点到这条直线的垂线段的长度,叫点到直线的距离.
小试牛刀
1、如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B.45°
C.55° D.65°
C
B
1
2
3
A
D
O
【答案】C
2、如图,△ABC中,CD是AB边上的高,CM是AB边上的中线,点C到边AB所在直线的距离是( )
A.线段CA的长度 B.线段CM的长度
C.线段CD的长度 D.线段CB的长度
【答案】C
小试牛刀
3、如图,分别过A、B、C作BC、AC、AB的垂线。
A
B
C
D
E
F
解:如图、AD⊥BC于D、BE⊥AC于E、CF⊥AB于F
A
C
E
B
D
O
1
∴ ∠EOB=90°(垂直的定义)
∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °
(
解:
∵ AB⊥OE (已知)
∵ ∠BOD= ∠1=55°
4、 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
(对顶角相等)
1、过点P 向线段AB 所在直线引垂线,正确的是( ).
A B C D
C
课堂练习
2、如图,已知直线CD,EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=______________.
30°
3、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为 .
C
A
B
E
F
D
32°
4、 点O是直线AB上的一点, OC是射线,OE平分∠AOC, OF平分∠BOC,试确定OE与OF的位置关系.并说明理由.
A
B
O
C
E
F
1
2
5、如图,直线 AB,CD 相交于点 O,OE⊥AB, ∠1 = 75°,求∠EOC 的度数.
解:∵ OE⊥AB,
∴∠AOE=90°(垂直的定义).
A
C
E
B
D
O
1
归纳总结
判断两直线(线段、射线所在直线)互相垂直,主要依据是垂直定义,只要说明两条相交直线所构成的四个角中有一个角是直角即可.
课堂总结
知识小结
以下几个方面由学生自己总结:
① 垂线的定义及垂直的符号表示;
② 垂线的有关性质;
③过一点作已知直线的垂线的方法.
课堂总结
5.1.2垂线
【学习目标】
1.理解垂线段的概念、“垂线段最短”的性质;
2.理解点到直线的距离的意义并会度量点到直线的距离。
两条直线相交
一般情况
对顶角:相等
邻补角:互补
B
A
C
D
O
1
2
3
4
特殊情况
复习:
固定木条a,转动木条b,当b的位置变化时,a、b所成的角是如何变化的
其中会有特殊情况吗
当这种情况出现时,a、b所成的四个角有什么特殊关系
我们会发现,ab所成的角由小变大再由大变小。
当∠α的角度为90°时,ab垂直。
当垂直时ab所成的四个角都是90°
新课讲解
1.垂直定义:
在相交线的模型(上图)中,固定木条a、转动木条b、当b的位置变化时.a.b所成的∠α也会发生变化,当∠α=90°时,我们说a与b互相垂直,记作a⊥b.
2.分清“互相垂直”与“垂线”的区别与联系:
“互相垂直”指两条直线的位置关系;
“垂线”是指其中一条直线对另一条直线的命名。
3.垂直的表示法:
“直线AB垂直于直线CD,垂足为O”,记为AB⊥CD,垂足为O,AB是CD的垂线,CD也是AB的垂线,他们互为垂线!
画一条直线L,画出L的垂线
问:还能画出L的垂线吗 能画几条
再问:怎样才能确定直线L的垂线位置
4.画图探究
直线L
■
O
(2) 经过直线L外一点B画直线L的垂线,这样的垂线能画出几条
A
·
经过直线上或者是外一点有且只有一条直线与已知直线垂直.
垂线性质1:过一点有且只有一条直线与已知直线垂直.
5.问题:要把河中的水引到农田P处,如何挖渠能使渠道最短
·p
提示,上学期我们曾经学过什么最短的知识,还记得吗
两点间线段最短.
如果把渠道看成直线L,连接直线L外一点P与直线L上各点的线段中,哪一条最短
L
如图所示,PC最短!连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.(PC的长)
判断以下两条直线是否垂直:
①两条直线相交所成的四个角中有一个是直角;
②两条直线相交所成的四个角相等;
③两条直线相交,有一组邻补角相等;
④两条直线相交,对顶角互补.
√
√
√
√
性质
点到直线的距离:
直线外一点到这条直线的垂线段的长度,叫点到直线的距离.
小试牛刀
1、如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B.45°
C.55° D.65°
C
B
1
2
3
A
D
O
【答案】C
2、如图,△ABC中,CD是AB边上的高,CM是AB边上的中线,点C到边AB所在直线的距离是( )
A.线段CA的长度 B.线段CM的长度
C.线段CD的长度 D.线段CB的长度
【答案】C
小试牛刀
3、如图,分别过A、B、C作BC、AC、AB的垂线。
A
B
C
D
E
F
解:如图、AD⊥BC于D、BE⊥AC于E、CF⊥AB于F
A
C
E
B
D
O
1
∴ ∠EOB=90°(垂直的定义)
∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °
(
解:
∵ AB⊥OE (已知)
∵ ∠BOD= ∠1=55°
4、 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
(对顶角相等)
1、过点P 向线段AB 所在直线引垂线,正确的是( ).
A B C D
C
课堂练习
2、如图,已知直线CD,EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=______________.
30°
3、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为 .
C
A
B
E
F
D
32°
4、 点O是直线AB上的一点, OC是射线,OE平分∠AOC, OF平分∠BOC,试确定OE与OF的位置关系.并说明理由.
A
B
O
C
E
F
1
2
5、如图,直线 AB,CD 相交于点 O,OE⊥AB, ∠1 = 75°,求∠EOC 的度数.
解:∵ OE⊥AB,
∴∠AOE=90°(垂直的定义).
A
C
E
B
D
O
1
归纳总结
判断两直线(线段、射线所在直线)互相垂直,主要依据是垂直定义,只要说明两条相交直线所构成的四个角中有一个角是直角即可.
课堂总结
知识小结
以下几个方面由学生自己总结:
① 垂线的定义及垂直的符号表示;
② 垂线的有关性质;
③过一点作已知直线的垂线的方法.
课堂总结
