7.3万有引力的理论成就课件(共27张PPT)
文档属性
| 名称 | 7.3万有引力的理论成就课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-23 08:32:53 | ||
图片预览








文档简介
(共27张PPT)
7.3 万有引力的理论成就
第7章 万有引力与宇宙航行
一、课题导入
“称量地球的质量”
卡文迪什
我能称量地球质量!!!
核心素养
重点:理清计算天体质量的两种思路
难点:掌握综合运用万有引力定律和圆周运动学知识分析天体问题的方法
重难点
物理观念:
1、了解万有引力定律在天文学上的重要应用。
2、会用万有引力定律计算天体质量,了解”称量天体质量” 和”计算太阳质量”的思路。
科学思维:
经历探究计算天体质量的过程,培养学生独立思考相互合作意识,提升学生学习能力;体会万有引力定律经受实践检验。
科学态度与责任:
通过学习使学生了解科学发展的曲折,深刻体会科学规律对人类探索未知世界的作用,激发学生对科学探究的兴趣,培养学生热爱科学的情感。
(1)物体做圆周运动的向心力公式是什么?分别写出向心力与线速度、角速度以及周期的关系式。
(2)万有引力定律的内容是什么?如何用公式表示?
(3)重力和万有引力的关系?(回顾重力定义,体会与万有引力细微区别,巩固地球表面物体的重力与地球对物体万有引力的关系。)
二、温故而知新
θ
Fn
R
M
G
m
w
r
F引
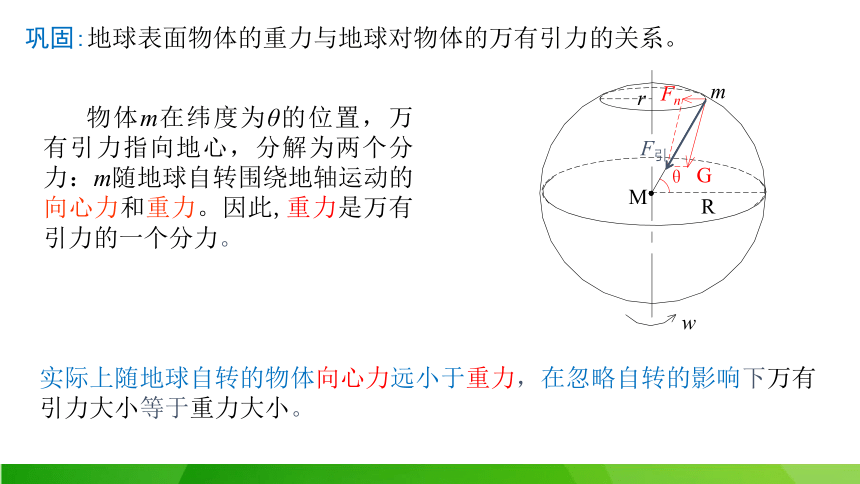
巩固:地球表面物体的重力与地球对物体的万有引力的关系。
物体m在纬度为θ的位置,万有引力指向地心,分解为两个分力:m随地球自转围绕地轴运动的向心力和重力。因此,重力是万有引力的一个分力。
实际上随地球自转的物体向心力远小于重力,在忽略自转的影响下万有引力大小等于重力大小。
三、独立自学
阅读课本并思考:万有引力在天文学上有哪些方面的应用呢?
1、能测出地球的质量和密度吗?怎样测
2、能测出太阳的质量和密度吗?怎样测
3、万有引力在天文学上还有其他的应用吗?
补充:球体的体积公式为:
“科学真是迷人”-测地球的质量
问题一:卡文迪什被称为能“称量地球的质量”的人,那么他测出G后我们如何得到地球质量的呢?万有引力定律是否能给我们提供帮助呢
引导探究一
不考虑地
球自转哦!!!
卡文迪什时代已经知道:
地表重力加速度:g = 9.8m/s2
地球半径: R = 6400km
引力常量: G=6.67×10-11Nm2/kg2
四、合作探究
1、“测量地球的质量”
不考虑地球自转的影响在地球表面附近质量为m的物体 G重=F引
所以说只要测出G就可以测出地球的质量。
知识迁移:此方法也适合求其它天体质量
g——地球表面的重力加速度
R——地球的半径
思考:用同样的方法如何来测其它天体的质量呢
四、合作探究
假如你被送到月球上,且已经知道月球半径和引力常量,给你一只弹簧秤和一个已知质量的砝码,你能否测出月球的质量?怎样测定?
方案:
1、先测出砝码在月球表面所受的重力
3、代入公式
2、再算出月球表面的重力加速度g
即可求得
四、合作探究
合作探究一
求某天体质量方法一:“在天体表面上想方法”
不考虑天体自转的影响:
即已知三个量g、R、G三个量就可以求
此时地球的密度你会求吗?
黄金代换:
四、合作探究
问题二:如何才能知道太阳的质量呢?
引导探究二
行星圆周运动由太阳和行星间的万有引力提供向心力,若我们可以测出太阳某行星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?
我们能在太阳的表面吗?
上面的方法可行吗?
四、合作探究
2、计算太阳的质量
我们可以测出太阳某行星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?思路是什么?(思考)
特点:需知道待求中心天体(M)的某一环绕天体的运行规律,且与环绕天体的质量(m)无关
注意: 此方法只可求出中心天体的质量,求不出环绕天体的质量!!!
1.将行星的运动看成是匀速圆周运动.
2.万有引力提供向心力: F引=Fn
四、合作探究
求天体质量方法二:“在天上想方法”
已知:m(环绕天体)绕着M(中心天体)转,测出m运动周期T和绕中心天体M的轨道半径r就可求出中心天体M:
F引=Fn
将环绕天体m的运动看作匀速圆周运动;万有引力充当向心力 F引=F向
四、合作探究
ρ
若环绕天体在中心天体表面运动则r=R
既然我们已经知道如何测中心天体质量那么它的密度怎么测?
计算地球的质量,除了一开始的方法外,还可以怎么求?
借助于月球,那么需要知道哪些量?
月球绕地球运行的周期T=27.3天,
月球与地球球心的平均距离r=3.84×108m
=6.0×1024kg
合作探究二
四、合作探究
万有引力理论的巨大成就
☆预见并发现未知行星,更是万有引力理论威力和价值的最生动例证。
☆把“天上的物理”与“地上的物理”完美的统一起来。
天上人间服从共同的科学法则
请阅读课本“发现未知天体”,明确如下问题:
问题:笔尖下发现的行星是哪一颗行星?如何发现?
(1)现象——问题的发现
(2)几种观点——猜想与假设
(3)亚当斯和勒维耶的计算及预言——科学推理.
(4)伽勒的发现——实践检验
3、发现未知天体
五、自主学习
小结:基本思路
1. “地上一条路”:在星体表面附近 F引=G重
2.“天上一条路”:将行星(或卫星)的运动看成是匀速圆周运动.
万有引力充当向心力 F引=F向.
不考虑星球的自转,星球表面及附近的物体所受重力等于星球对物体的万有引力。
物理模型(一)
环绕天体m绕中心天体M做匀速圆周运动
物理模型(二)
若已知宇宙飞船绕海王星运动的轨道半径为r,周期为T,引力常量为G,则由此可求出 ( )
A、宇宙飞船的质量 B、海王星的质量
C、海王星的密度 D、宇宙飞船的密度
B
利用
求解问题时,该式与环绕体质量m无关,与中心体质量M有关。
当堂诊学
利用下列哪组数据可以计算出地球的质量,引力常量G已知( )
A:已知地球的半径R和地球表面的重力加速度g
B:已知卫星围绕地球运动的轨道半径r和周期T
C:已知卫星围绕地球运动的轨道半径r和线速度V
D:已知卫星围绕地球运动的线速度V和周期T
E:已知地球绕太阳运动的周期及地球离太阳的距离
ABCD
举一反三
2、(多选)已知万有引力常量G,现在给出下列各组数据,可以计算出地球质量的是 ( )
A、已知地球的半径R和地面的重力加速度g
B、已知卫星绕地球做匀速圆周运动的轨道半径r和线速度v
C、已知卫星绕地球做匀速圆周运动的轨道半径r和周期T
D、地球公转的周期T及运转半径r
1、若已知太阳的一个行星绕太阳运转的轨道半径为r,
周期为T,引力常数为G,则可求得 ( )
A.该行星的质量 B.太阳的质量
C.该行星的平均密度 D.太阳的平均密度
课堂检测
3、一宇航员为了估测一星球的质量,他在该星球的表面做自由落体实验:让小球在离地面h高处自由下落,他测出经时间t小球落地,又已知该星球的半径为R,试估算该星球的质量。
课堂检测
(答案:2hR2/Gt2)
作业:学习指导:P.47--49
本节课到此结束,谢谢!
7.3 万有引力的理论成就
第7章 万有引力与宇宙航行
一、课题导入
“称量地球的质量”
卡文迪什
我能称量地球质量!!!
核心素养
重点:理清计算天体质量的两种思路
难点:掌握综合运用万有引力定律和圆周运动学知识分析天体问题的方法
重难点
物理观念:
1、了解万有引力定律在天文学上的重要应用。
2、会用万有引力定律计算天体质量,了解”称量天体质量” 和”计算太阳质量”的思路。
科学思维:
经历探究计算天体质量的过程,培养学生独立思考相互合作意识,提升学生学习能力;体会万有引力定律经受实践检验。
科学态度与责任:
通过学习使学生了解科学发展的曲折,深刻体会科学规律对人类探索未知世界的作用,激发学生对科学探究的兴趣,培养学生热爱科学的情感。
(1)物体做圆周运动的向心力公式是什么?分别写出向心力与线速度、角速度以及周期的关系式。
(2)万有引力定律的内容是什么?如何用公式表示?
(3)重力和万有引力的关系?(回顾重力定义,体会与万有引力细微区别,巩固地球表面物体的重力与地球对物体万有引力的关系。)
二、温故而知新
θ
Fn
R
M
G
m
w
r
F引
巩固:地球表面物体的重力与地球对物体的万有引力的关系。
物体m在纬度为θ的位置,万有引力指向地心,分解为两个分力:m随地球自转围绕地轴运动的向心力和重力。因此,重力是万有引力的一个分力。
实际上随地球自转的物体向心力远小于重力,在忽略自转的影响下万有引力大小等于重力大小。
三、独立自学
阅读课本并思考:万有引力在天文学上有哪些方面的应用呢?
1、能测出地球的质量和密度吗?怎样测
2、能测出太阳的质量和密度吗?怎样测
3、万有引力在天文学上还有其他的应用吗?
补充:球体的体积公式为:
“科学真是迷人”-测地球的质量
问题一:卡文迪什被称为能“称量地球的质量”的人,那么他测出G后我们如何得到地球质量的呢?万有引力定律是否能给我们提供帮助呢
引导探究一
不考虑地
球自转哦!!!
卡文迪什时代已经知道:
地表重力加速度:g = 9.8m/s2
地球半径: R = 6400km
引力常量: G=6.67×10-11Nm2/kg2
四、合作探究
1、“测量地球的质量”
不考虑地球自转的影响在地球表面附近质量为m的物体 G重=F引
所以说只要测出G就可以测出地球的质量。
知识迁移:此方法也适合求其它天体质量
g——地球表面的重力加速度
R——地球的半径
思考:用同样的方法如何来测其它天体的质量呢
四、合作探究
假如你被送到月球上,且已经知道月球半径和引力常量,给你一只弹簧秤和一个已知质量的砝码,你能否测出月球的质量?怎样测定?
方案:
1、先测出砝码在月球表面所受的重力
3、代入公式
2、再算出月球表面的重力加速度g
即可求得
四、合作探究
合作探究一
求某天体质量方法一:“在天体表面上想方法”
不考虑天体自转的影响:
即已知三个量g、R、G三个量就可以求
此时地球的密度你会求吗?
黄金代换:
四、合作探究
问题二:如何才能知道太阳的质量呢?
引导探究二
行星圆周运动由太阳和行星间的万有引力提供向心力,若我们可以测出太阳某行星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?
我们能在太阳的表面吗?
上面的方法可行吗?
四、合作探究
2、计算太阳的质量
我们可以测出太阳某行星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?思路是什么?(思考)
特点:需知道待求中心天体(M)的某一环绕天体的运行规律,且与环绕天体的质量(m)无关
注意: 此方法只可求出中心天体的质量,求不出环绕天体的质量!!!
1.将行星的运动看成是匀速圆周运动.
2.万有引力提供向心力: F引=Fn
四、合作探究
求天体质量方法二:“在天上想方法”
已知:m(环绕天体)绕着M(中心天体)转,测出m运动周期T和绕中心天体M的轨道半径r就可求出中心天体M:
F引=Fn
将环绕天体m的运动看作匀速圆周运动;万有引力充当向心力 F引=F向
四、合作探究
ρ
若环绕天体在中心天体表面运动则r=R
既然我们已经知道如何测中心天体质量那么它的密度怎么测?
计算地球的质量,除了一开始的方法外,还可以怎么求?
借助于月球,那么需要知道哪些量?
月球绕地球运行的周期T=27.3天,
月球与地球球心的平均距离r=3.84×108m
=6.0×1024kg
合作探究二
四、合作探究
万有引力理论的巨大成就
☆预见并发现未知行星,更是万有引力理论威力和价值的最生动例证。
☆把“天上的物理”与“地上的物理”完美的统一起来。
天上人间服从共同的科学法则
请阅读课本“发现未知天体”,明确如下问题:
问题:笔尖下发现的行星是哪一颗行星?如何发现?
(1)现象——问题的发现
(2)几种观点——猜想与假设
(3)亚当斯和勒维耶的计算及预言——科学推理.
(4)伽勒的发现——实践检验
3、发现未知天体
五、自主学习
小结:基本思路
1. “地上一条路”:在星体表面附近 F引=G重
2.“天上一条路”:将行星(或卫星)的运动看成是匀速圆周运动.
万有引力充当向心力 F引=F向.
不考虑星球的自转,星球表面及附近的物体所受重力等于星球对物体的万有引力。
物理模型(一)
环绕天体m绕中心天体M做匀速圆周运动
物理模型(二)
若已知宇宙飞船绕海王星运动的轨道半径为r,周期为T,引力常量为G,则由此可求出 ( )
A、宇宙飞船的质量 B、海王星的质量
C、海王星的密度 D、宇宙飞船的密度
B
利用
求解问题时,该式与环绕体质量m无关,与中心体质量M有关。
当堂诊学
利用下列哪组数据可以计算出地球的质量,引力常量G已知( )
A:已知地球的半径R和地球表面的重力加速度g
B:已知卫星围绕地球运动的轨道半径r和周期T
C:已知卫星围绕地球运动的轨道半径r和线速度V
D:已知卫星围绕地球运动的线速度V和周期T
E:已知地球绕太阳运动的周期及地球离太阳的距离
ABCD
举一反三
2、(多选)已知万有引力常量G,现在给出下列各组数据,可以计算出地球质量的是 ( )
A、已知地球的半径R和地面的重力加速度g
B、已知卫星绕地球做匀速圆周运动的轨道半径r和线速度v
C、已知卫星绕地球做匀速圆周运动的轨道半径r和周期T
D、地球公转的周期T及运转半径r
1、若已知太阳的一个行星绕太阳运转的轨道半径为r,
周期为T,引力常数为G,则可求得 ( )
A.该行星的质量 B.太阳的质量
C.该行星的平均密度 D.太阳的平均密度
课堂检测
3、一宇航员为了估测一星球的质量,他在该星球的表面做自由落体实验:让小球在离地面h高处自由下落,他测出经时间t小球落地,又已知该星球的半径为R,试估算该星球的质量。
课堂检测
(答案:2hR2/Gt2)
作业:学习指导:P.47--49
本节课到此结束,谢谢!
