2021-2022学年度高一下数学一课一练8.3简单几何体的表面积和体积 (word含解析)
文档属性
| 名称 | 2021-2022学年度高一下数学一课一练8.3简单几何体的表面积和体积 (word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 717.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 08:48:39 | ||
图片预览



文档简介
8.3简单几何体的表面积和体积
一、单选题
1.在直三棱柱中,,则三棱柱外接球体积等于( )
A. B. C. D.
2.《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马.若四棱锥为阳马,已知面,,四棱锥的顶点都在球的球面上,则球的表面积为( )
A. B. C. D.
3.我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.“鳖臑”指的是四个面都是直角三角形的三棱锥.“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以 ,其形露矣.”现有一如图所示的“堑堵”即三棱柱,其中,若,当“阳马”即四棱锥体积最大时,“堑堵”即三棱柱的外接球的表面积为( )
A. B. C. D.
4.三棱锥的底面是边长为3的正三角形,,则三棱锥的体积等于( )
A. B. C. D.
5.若两个正四面体的顶点都是一个体积为1的正方体的顶点,则这两个四面体的公共部分的体积为( )
A. B. C. D.
6.已知平面垂直于平面,四边形为菱形,,,,,三棱锥的顶点都在球O上,则球O的表面积为( )
A. B. C. D.
7.已知球的半径为1,是球的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
8.正四面体是一种柏拉图多面体,正四面体与自身对偶;正四面体的重心,四条高的交点,外接球、内切球球心共点.4个半径为1的小球装入一个正四面体内,下列四个结论中错误的是( )
A.四面体最小体积
B.四面体最小表面积
C.四面体最短棱长
D.四面体最小高
9.斗笠,用竹篾夹油纸或竹叶粽丝等编织,是人们遮阳光和雨的工具.某斗笠的三视图如图所示(单位:),若该斗笠水平放置,雨水垂直下落,则该斗笠被雨水打湿的面积为( )
A. B.
C. D.
10.已知,是球的球面上两点,,为该球面上的动点,若三棱锥体积的最大值为,则球的表面积为( )
A. B. C. D.
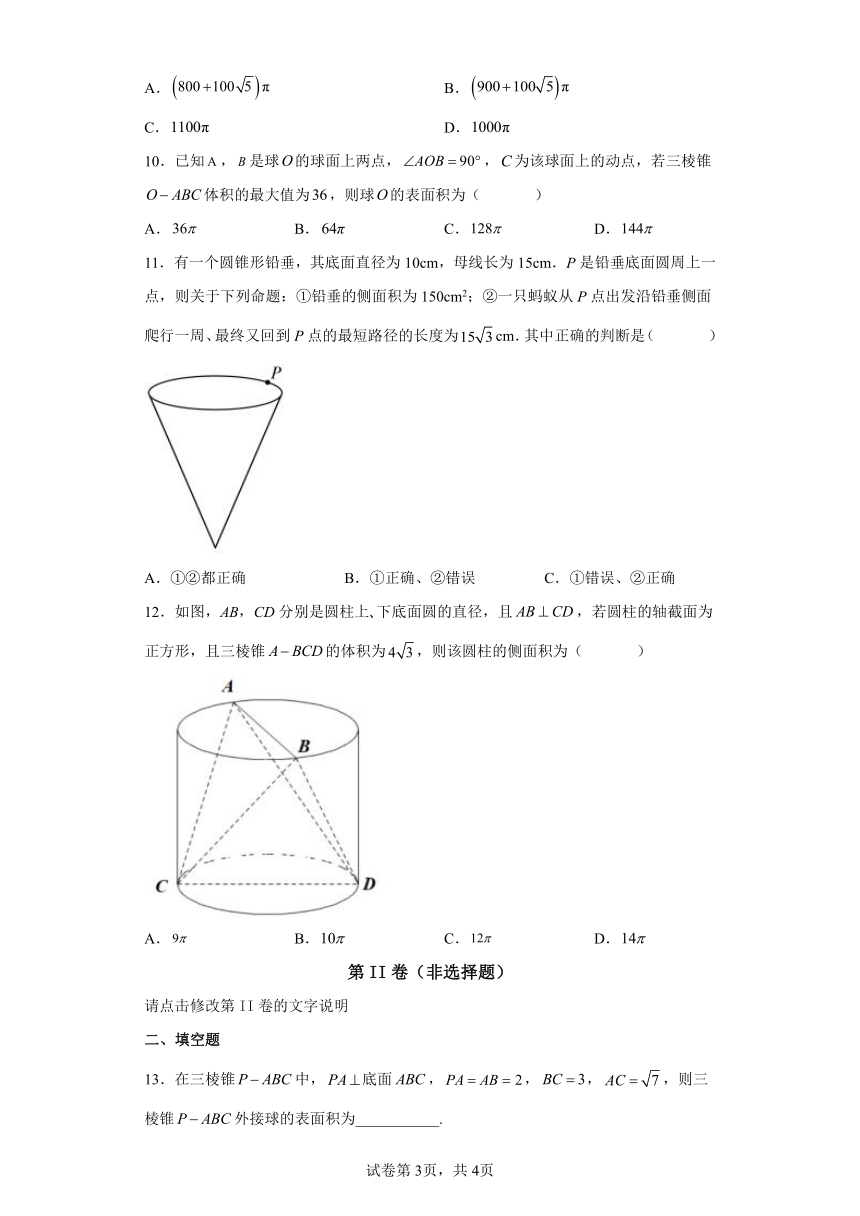
11.有一个圆锥形铅垂,其底面直径为10cm,母线长为15cm.P是铅垂底面圆周上一点,则关于下列命题:①铅垂的侧面积为150cm2;②一只蚂蚁从P点出发沿铅垂侧面爬行一周、最终又回到P点的最短路径的长度为cm.其中正确的判断是( )
A.①②都正确 B.①正确、②错误 C.①错误、②正确
12.如图,AB,CD分别是圆柱上 下底面圆的直径,且,若圆柱的轴截面为正方形,且三棱锥的体积为,则该圆柱的侧面积为( )
A. B. C. D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
13.在三棱锥中,底面,,,,则三棱锥外接球的表面积为___________.
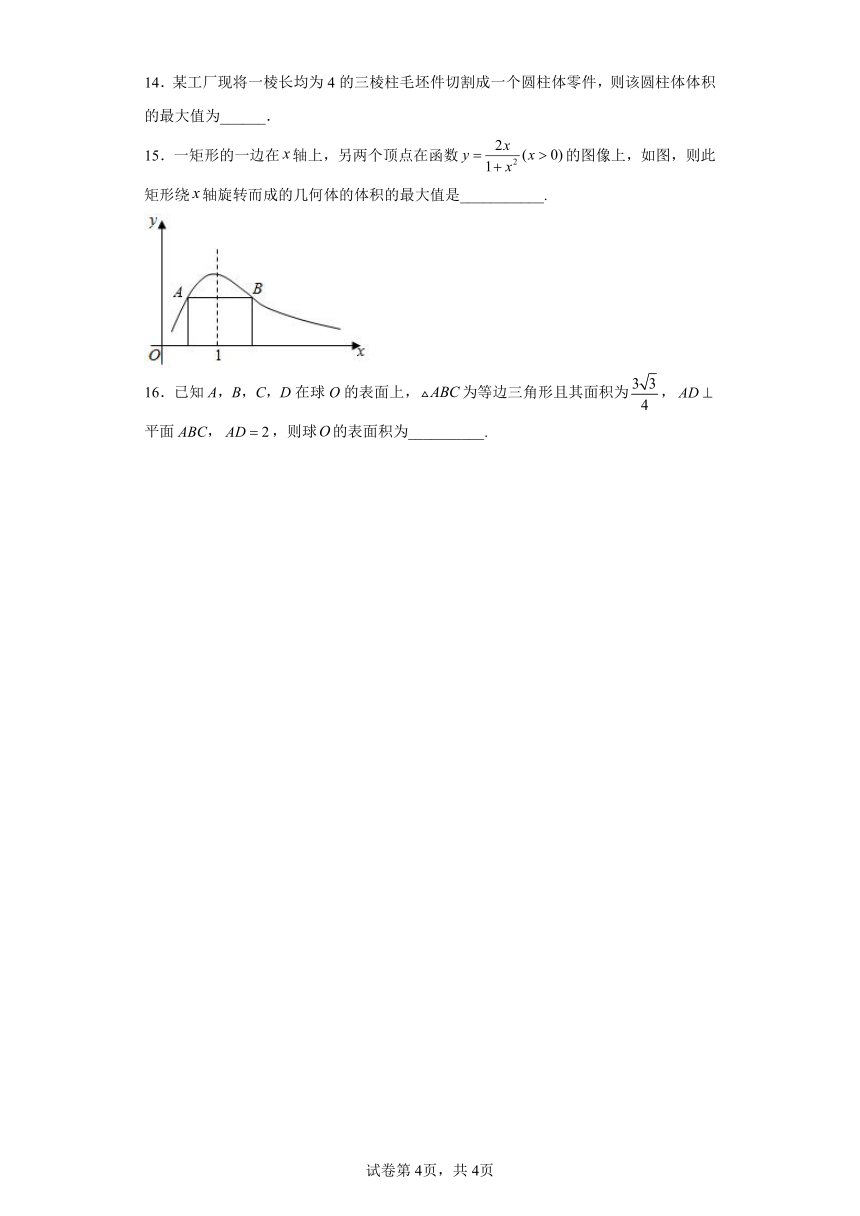
14.某工厂现将一棱长均为4的三棱柱毛坯件切割成一个圆柱体零件,则该圆柱体体积的最大值为______.
15.一矩形的一边在轴上,另两个顶点在函数的图像上,如图,则此矩形绕轴旋转而成的几何体的体积的最大值是___________.
16.已知A,B,C,D在球O的表面上,为等边三角形且其面积为,平面ABC,,则球的表面积为__________.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
根据给定条件将直三棱柱补形成正方体,借助正方体求其外接球半径计算作答.
【详解】
在直三棱柱中,因,即,则,
于是得,将其补形成棱长为2的正方体,如图,
则直三棱柱的外接球即为棱长为2的正方体的外接球,
球半径,因此,,
所以三棱柱外接球体积等于.
故选:A
2.C
【解析】
【分析】
由题意,将四棱锥补形为正方体,则四棱锥外接球的直径即为正方体的体对角线长,最后根据球的面积公式即可得答案.
【详解】
解:由题意,因为面,所以,,又,,所以将四棱锥放置在如图所示的正方体中,
则正方体的外接球即为四棱锥的外接球,
所以四棱锥的外接球直径为,
所以球的表面积为,
故选:C.
3.B
【解析】
【分析】
设,得到,当四棱锥体积取得最大值时,根据基本不等式得到,利用三棱柱的外接球的球心为的中点,求得球的半径,结合球的表面积公式,即可求解.
【详解】
设,
因为,则,
所以四棱锥的体积为,
当且仅当时,等号成立,
此时三棱柱的外接球的球心为的中点,
所以外接球的半径为,
所以三棱柱的外接球的表面积为.
故选:B.
4.A
【解析】
【分析】
将三棱锥翻转为,确定顶点A在底面的射影为斜边的中点,利用勾股定理求出,然后由三棱锥的体积公式即可求解.
【详解】
解:将三棱锥翻转一下,如图所示,
因为,所以,所以为直角三角形,
由斜线长相等,则射影长相等,可得点A在平面内的射影为直角三角形的外心,
所以为直角斜边的中点,且平面,则为三棱锥的高,
由勾股定理可得,
所以三棱锥的体积.
故选:A.
5.D
【解析】
【分析】
首先画出示意图得到公共部分几何体的结构,接着根据体积公式求解即可.
【详解】
解:因为两个正四面体的顶点都是一个体积为1的正方体的顶点,
所以两个正四面体的顶点都是一个棱长为1的正方体的顶点,
故画出示意图如下:
由图可得这两个正四面体公共部分为八面体,
该八面体是由两个正四棱锥和组成,
根据正方体的对称性可得四边形为边长为的正方形,
正四棱锥和的高为正方体棱长的一半,即等于,
则,
故选:D.
6.A
【解析】
【分析】
由题意知,球心平面,取线段的中点为,可计算得球心直线
以为原点,分别为轴,建立空间直角坐标系,根据可求出球的半径,即可求出答案.
【详解】
空间中到两点距离相等的点的集合为平面,
所以球心平面,
在平面上到两点距离相等的点的集合为线段的垂直平分线.取线段的中点为,
∵,∴,
由余弦定理得,,
∴,
故为线段的垂直平分线,
所以球心直线
取的中点为,以为原点,分别为轴,建立空间直角坐标系,
设,,,O是球心,只需要使,
即,
解得:,所以,
所以.
故选:A.
7.C
【解析】
【分析】
由球的截面性质求得球心到平面的距离,即棱锥的高,然后计算体积.
【详解】
解:的外接圆半径为,从而三棱锥的高为
故选:C
8.A
【解析】
【分析】
当四球与正四面体内切,且四球两两相切时相关量最小,在此状态下,内切球球心构成正四面体,棱长为2,求出小正四面体与大正四面体的相似比得解.
【详解】
由题可知,正四面体体积、表面积、棱长、高达到最小时, 四个球两两相切且与正四面体都相切,设此时正四面体为,内切四球球心构成棱长为2的正四面体.
正四面体中,高为,为中点,,
为直线与面所成角,,
正四面体的表面积为;
正四面体的体积为
球与正四面体内切,为切点,,
因为,所以,
所以正四面体的高为:,
两个正四面体的相似比为:,
所以正四面体的最小体积为:,A错;
正四面体的最小表面积为:,B正确;
正四面体的最小棱长为:,C正确;
正四面体的最小高为:.
故选;A.
9.A
【解析】
【分析】
根据三视图可知,该几何体是由一个底面半径为10,高为20的圆锥和宽度为20的圆环组成的几何体,则所求面积积为圆锥的侧面积与圆环的面积之和
【详解】
根据三视图可知,该几何体是由一个底面半径为10,高为20的圆锥和宽度为20的圆环组成的几何体,所以该斗笠被雨水打湿的面积为
,
故选:A
10.D
【解析】
【分析】
根据给定条件确定出三棱锥体积最大时的点C位置,再求出球半径即可得解.
【详解】
设球的半径为,因,则的面积,
而,且面积为定值,则当点到平面的距离最大时,最大,
于是,当是与球的大圆面垂直的直径的端点时,三棱锥体积最大,最大值为,解得,
所以球的表面积为.
故选:D
11.C
【解析】
【分析】
根据圆锥的侧面展开图为扇形,由扇形的面积公式计算即可判断①,在展开图中可知沿着爬行即为最短路径,计算即可判断②.
【详解】
直径为10cm,母线长为15cm.
底面圆周长为.
将其侧面展开后得到扇形半径为cm,孤长为,则扇形面积为,①错误.
将其侧面展开,则爬行最短距离为,由孤长公式得展开后扇形弧度数为,作,,又,
,
cm,②正确.
故选:C
12.C
【解析】
【分析】
分别取上下底面的圆心为,连接,可得平面,设圆柱上底面圆的半径为, 三棱锥的体积为,求出a,由圆柱的侧面积公式可得答案.
【详解】
分别取上下底面的圆心为,连接,则,
因为,所以,且,
所以平面,设圆柱上底面圆的半径为,则,
三棱锥的体积为,
解得,该圆柱的侧面积为,
故选:C.
13.
【解析】
【分析】
计算出外接圆的半径,利用公式可求得三棱锥的外接球的半径,再利用球体的表面积公式可求得结果.
【详解】
如下图所示:
圆柱的底面圆直径为,母线长为,则的中点到圆柱底面圆上每点的距离都相等,
则为圆柱的外接球球心,且有,
底面,可将三棱锥置于圆柱内,其中圆为的外接圆,
由余弦定理可得,,则,
则外接圆的直径,则,
所以三棱锥外接球的半径,
故三棱锥外接球的表面积为.
故答案为:.
14.
【解析】
【分析】
圆柱体体积最大时,圆柱的上下底面分别在三棱柱的上下底面上,且圆柱与三棱柱的侧面均相切.根据等边三角形求出其内切圆的半径,从而得出答案.
【详解】
解:圆柱体体积最大时,圆柱的上下底面分别在三棱柱的上下底面上,且圆柱与三棱柱的侧面均相切.
设圆柱的底面半径为,由题意可知圆柱底面圆即为三棱柱的底面等边三角形的内切圆.
如图所示:设为圆柱底面圆与三棱柱的底面等边三角形的一个切点,则为中点.
所以,即
圆柱体体积最大值为:
故答案为:.
15.
【解析】
【分析】
先利用基本不等式求出的取值范围,再设点,的坐标,由,的纵坐标相同,得到,从而得到,再利用圆柱的体积公式以及基本不等式,即可得到答案.
【详解】
由,又,则,当且仅当时取等号,
∴,且,
∵矩形绕轴旋转而成的几何体为圆柱,设,,,,如图所示,
则圆柱的底面圆的半径为,高为,且,,
∴,即,由,可得,
∴,故,
∴圆柱的体积为,当且仅当时取等号,
∴此矩形绕轴旋转而成的几何体的体积的最大值是.
故答案为:.
16.
【解析】
【分析】
由正弦定理可得外接圆的半径,利用勾股定理可得四面体的外接球的半径,即可求出球的表面积.
【详解】
因为为等边三角形且其面积为,
所以的边长为,
由正弦定理可得外接圆的半径为,
平面,,
四面体的外接球的半径为,
球的表面积为.
故答案为:
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在直三棱柱中,,则三棱柱外接球体积等于( )
A. B. C. D.
2.《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马.若四棱锥为阳马,已知面,,四棱锥的顶点都在球的球面上,则球的表面积为( )
A. B. C. D.
3.我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.“鳖臑”指的是四个面都是直角三角形的三棱锥.“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以 ,其形露矣.”现有一如图所示的“堑堵”即三棱柱,其中,若,当“阳马”即四棱锥体积最大时,“堑堵”即三棱柱的外接球的表面积为( )
A. B. C. D.
4.三棱锥的底面是边长为3的正三角形,,则三棱锥的体积等于( )
A. B. C. D.
5.若两个正四面体的顶点都是一个体积为1的正方体的顶点,则这两个四面体的公共部分的体积为( )
A. B. C. D.
6.已知平面垂直于平面,四边形为菱形,,,,,三棱锥的顶点都在球O上,则球O的表面积为( )
A. B. C. D.
7.已知球的半径为1,是球的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
8.正四面体是一种柏拉图多面体,正四面体与自身对偶;正四面体的重心,四条高的交点,外接球、内切球球心共点.4个半径为1的小球装入一个正四面体内,下列四个结论中错误的是( )
A.四面体最小体积
B.四面体最小表面积
C.四面体最短棱长
D.四面体最小高
9.斗笠,用竹篾夹油纸或竹叶粽丝等编织,是人们遮阳光和雨的工具.某斗笠的三视图如图所示(单位:),若该斗笠水平放置,雨水垂直下落,则该斗笠被雨水打湿的面积为( )
A. B.
C. D.
10.已知,是球的球面上两点,,为该球面上的动点,若三棱锥体积的最大值为,则球的表面积为( )
A. B. C. D.
11.有一个圆锥形铅垂,其底面直径为10cm,母线长为15cm.P是铅垂底面圆周上一点,则关于下列命题:①铅垂的侧面积为150cm2;②一只蚂蚁从P点出发沿铅垂侧面爬行一周、最终又回到P点的最短路径的长度为cm.其中正确的判断是( )
A.①②都正确 B.①正确、②错误 C.①错误、②正确
12.如图,AB,CD分别是圆柱上 下底面圆的直径,且,若圆柱的轴截面为正方形,且三棱锥的体积为,则该圆柱的侧面积为( )
A. B. C. D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
13.在三棱锥中,底面,,,,则三棱锥外接球的表面积为___________.
14.某工厂现将一棱长均为4的三棱柱毛坯件切割成一个圆柱体零件,则该圆柱体体积的最大值为______.
15.一矩形的一边在轴上,另两个顶点在函数的图像上,如图,则此矩形绕轴旋转而成的几何体的体积的最大值是___________.
16.已知A,B,C,D在球O的表面上,为等边三角形且其面积为,平面ABC,,则球的表面积为__________.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
根据给定条件将直三棱柱补形成正方体,借助正方体求其外接球半径计算作答.
【详解】
在直三棱柱中,因,即,则,
于是得,将其补形成棱长为2的正方体,如图,
则直三棱柱的外接球即为棱长为2的正方体的外接球,
球半径,因此,,
所以三棱柱外接球体积等于.
故选:A
2.C
【解析】
【分析】
由题意,将四棱锥补形为正方体,则四棱锥外接球的直径即为正方体的体对角线长,最后根据球的面积公式即可得答案.
【详解】
解:由题意,因为面,所以,,又,,所以将四棱锥放置在如图所示的正方体中,
则正方体的外接球即为四棱锥的外接球,
所以四棱锥的外接球直径为,
所以球的表面积为,
故选:C.
3.B
【解析】
【分析】
设,得到,当四棱锥体积取得最大值时,根据基本不等式得到,利用三棱柱的外接球的球心为的中点,求得球的半径,结合球的表面积公式,即可求解.
【详解】
设,
因为,则,
所以四棱锥的体积为,
当且仅当时,等号成立,
此时三棱柱的外接球的球心为的中点,
所以外接球的半径为,
所以三棱柱的外接球的表面积为.
故选:B.
4.A
【解析】
【分析】
将三棱锥翻转为,确定顶点A在底面的射影为斜边的中点,利用勾股定理求出,然后由三棱锥的体积公式即可求解.
【详解】
解:将三棱锥翻转一下,如图所示,
因为,所以,所以为直角三角形,
由斜线长相等,则射影长相等,可得点A在平面内的射影为直角三角形的外心,
所以为直角斜边的中点,且平面,则为三棱锥的高,
由勾股定理可得,
所以三棱锥的体积.
故选:A.
5.D
【解析】
【分析】
首先画出示意图得到公共部分几何体的结构,接着根据体积公式求解即可.
【详解】
解:因为两个正四面体的顶点都是一个体积为1的正方体的顶点,
所以两个正四面体的顶点都是一个棱长为1的正方体的顶点,
故画出示意图如下:
由图可得这两个正四面体公共部分为八面体,
该八面体是由两个正四棱锥和组成,
根据正方体的对称性可得四边形为边长为的正方形,
正四棱锥和的高为正方体棱长的一半,即等于,
则,
故选:D.
6.A
【解析】
【分析】
由题意知,球心平面,取线段的中点为,可计算得球心直线
以为原点,分别为轴,建立空间直角坐标系,根据可求出球的半径,即可求出答案.
【详解】
空间中到两点距离相等的点的集合为平面,
所以球心平面,
在平面上到两点距离相等的点的集合为线段的垂直平分线.取线段的中点为,
∵,∴,
由余弦定理得,,
∴,
故为线段的垂直平分线,
所以球心直线
取的中点为,以为原点,分别为轴,建立空间直角坐标系,
设,,,O是球心,只需要使,
即,
解得:,所以,
所以.
故选:A.
7.C
【解析】
【分析】
由球的截面性质求得球心到平面的距离,即棱锥的高,然后计算体积.
【详解】
解:的外接圆半径为,从而三棱锥的高为
故选:C
8.A
【解析】
【分析】
当四球与正四面体内切,且四球两两相切时相关量最小,在此状态下,内切球球心构成正四面体,棱长为2,求出小正四面体与大正四面体的相似比得解.
【详解】
由题可知,正四面体体积、表面积、棱长、高达到最小时, 四个球两两相切且与正四面体都相切,设此时正四面体为,内切四球球心构成棱长为2的正四面体.
正四面体中,高为,为中点,,
为直线与面所成角,,
正四面体的表面积为;
正四面体的体积为
球与正四面体内切,为切点,,
因为,所以,
所以正四面体的高为:,
两个正四面体的相似比为:,
所以正四面体的最小体积为:,A错;
正四面体的最小表面积为:,B正确;
正四面体的最小棱长为:,C正确;
正四面体的最小高为:.
故选;A.
9.A
【解析】
【分析】
根据三视图可知,该几何体是由一个底面半径为10,高为20的圆锥和宽度为20的圆环组成的几何体,则所求面积积为圆锥的侧面积与圆环的面积之和
【详解】
根据三视图可知,该几何体是由一个底面半径为10,高为20的圆锥和宽度为20的圆环组成的几何体,所以该斗笠被雨水打湿的面积为
,
故选:A
10.D
【解析】
【分析】
根据给定条件确定出三棱锥体积最大时的点C位置,再求出球半径即可得解.
【详解】
设球的半径为,因,则的面积,
而,且面积为定值,则当点到平面的距离最大时,最大,
于是,当是与球的大圆面垂直的直径的端点时,三棱锥体积最大,最大值为,解得,
所以球的表面积为.
故选:D
11.C
【解析】
【分析】
根据圆锥的侧面展开图为扇形,由扇形的面积公式计算即可判断①,在展开图中可知沿着爬行即为最短路径,计算即可判断②.
【详解】
直径为10cm,母线长为15cm.
底面圆周长为.
将其侧面展开后得到扇形半径为cm,孤长为,则扇形面积为,①错误.
将其侧面展开,则爬行最短距离为,由孤长公式得展开后扇形弧度数为,作,,又,
,
cm,②正确.
故选:C
12.C
【解析】
【分析】
分别取上下底面的圆心为,连接,可得平面,设圆柱上底面圆的半径为, 三棱锥的体积为,求出a,由圆柱的侧面积公式可得答案.
【详解】
分别取上下底面的圆心为,连接,则,
因为,所以,且,
所以平面,设圆柱上底面圆的半径为,则,
三棱锥的体积为,
解得,该圆柱的侧面积为,
故选:C.
13.
【解析】
【分析】
计算出外接圆的半径,利用公式可求得三棱锥的外接球的半径,再利用球体的表面积公式可求得结果.
【详解】
如下图所示:
圆柱的底面圆直径为,母线长为,则的中点到圆柱底面圆上每点的距离都相等,
则为圆柱的外接球球心,且有,
底面,可将三棱锥置于圆柱内,其中圆为的外接圆,
由余弦定理可得,,则,
则外接圆的直径,则,
所以三棱锥外接球的半径,
故三棱锥外接球的表面积为.
故答案为:.
14.
【解析】
【分析】
圆柱体体积最大时,圆柱的上下底面分别在三棱柱的上下底面上,且圆柱与三棱柱的侧面均相切.根据等边三角形求出其内切圆的半径,从而得出答案.
【详解】
解:圆柱体体积最大时,圆柱的上下底面分别在三棱柱的上下底面上,且圆柱与三棱柱的侧面均相切.
设圆柱的底面半径为,由题意可知圆柱底面圆即为三棱柱的底面等边三角形的内切圆.
如图所示:设为圆柱底面圆与三棱柱的底面等边三角形的一个切点,则为中点.
所以,即
圆柱体体积最大值为:
故答案为:.
15.
【解析】
【分析】
先利用基本不等式求出的取值范围,再设点,的坐标,由,的纵坐标相同,得到,从而得到,再利用圆柱的体积公式以及基本不等式,即可得到答案.
【详解】
由,又,则,当且仅当时取等号,
∴,且,
∵矩形绕轴旋转而成的几何体为圆柱,设,,,,如图所示,
则圆柱的底面圆的半径为,高为,且,,
∴,即,由,可得,
∴,故,
∴圆柱的体积为,当且仅当时取等号,
∴此矩形绕轴旋转而成的几何体的体积的最大值是.
故答案为:.
16.
【解析】
【分析】
由正弦定理可得外接圆的半径,利用勾股定理可得四面体的外接球的半径,即可求出球的表面积.
【详解】
因为为等边三角形且其面积为,
所以的边长为,
由正弦定理可得外接圆的半径为,
平面,,
四面体的外接球的半径为,
球的表面积为.
故答案为:
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
