人教版数学五年级下册第七单元《折线统计图》单元测试卷(含答案)
文档属性
| 名称 | 人教版数学五年级下册第七单元《折线统计图》单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 314.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 07:14:34 | ||
图片预览



文档简介
人教版数学五年级下册第七单元《折线统计图》单元测试卷
一、选择题
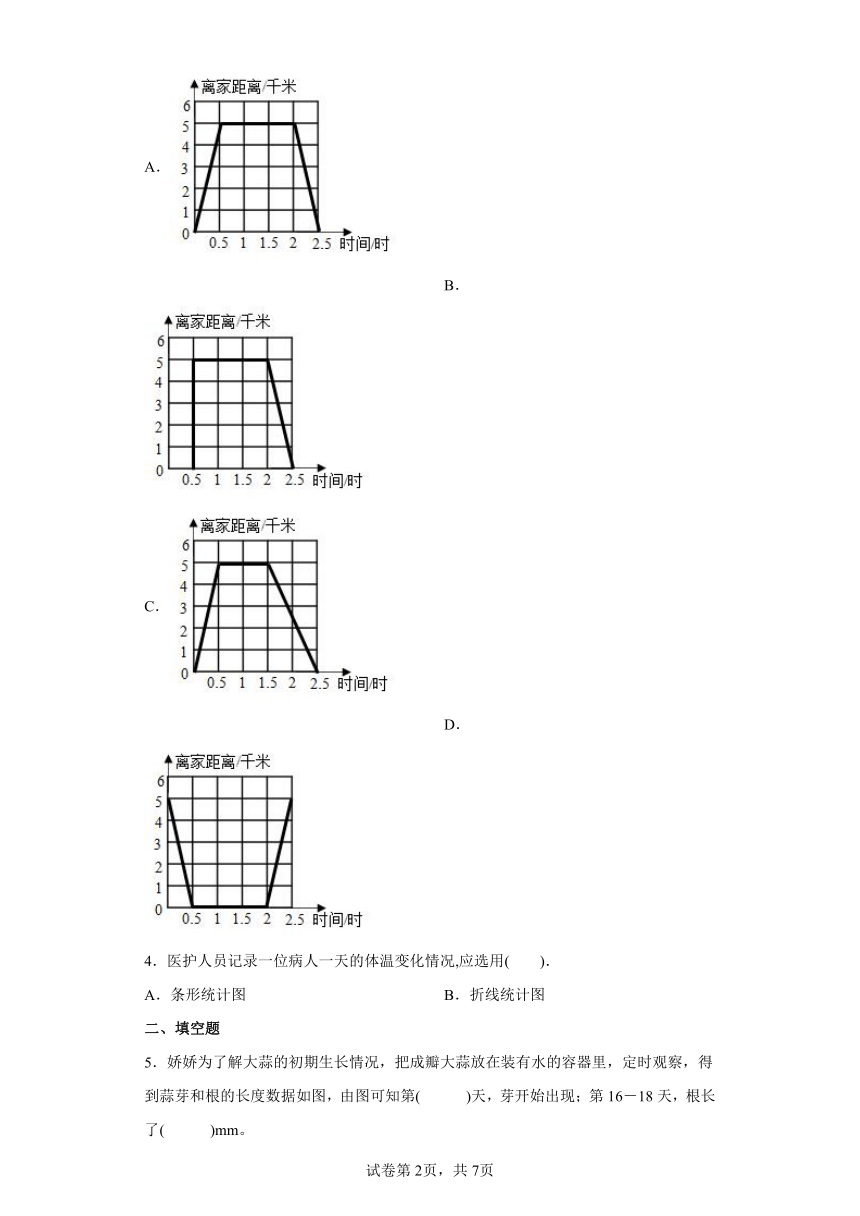
1.观察图中斑马和长颈鹿的奔跑情况,斑马比长颈鹿每分钟快( )千米。
A.0.4 B.0.8 C.4 D.8
2.珠海市规定:每年每户用气(天燃气)量不超过300立方米,每立方米3.45元;当用气量超过300立方米时,超过的部分每立方米为4.15元。下图中能正确表示每年用气费用与用气量关系的示意图是( )
A. B. C.
3.育才小学六年级同学从学校出发,乘车0.5时,来到离学校5千米远的科技馆,参观1时,出馆后休息0.5时,然后乘车0.5时返回学校.下面四幅图中,描述了育才小学六年级同学这一活动行程的是图( )
A. B.
C. D.
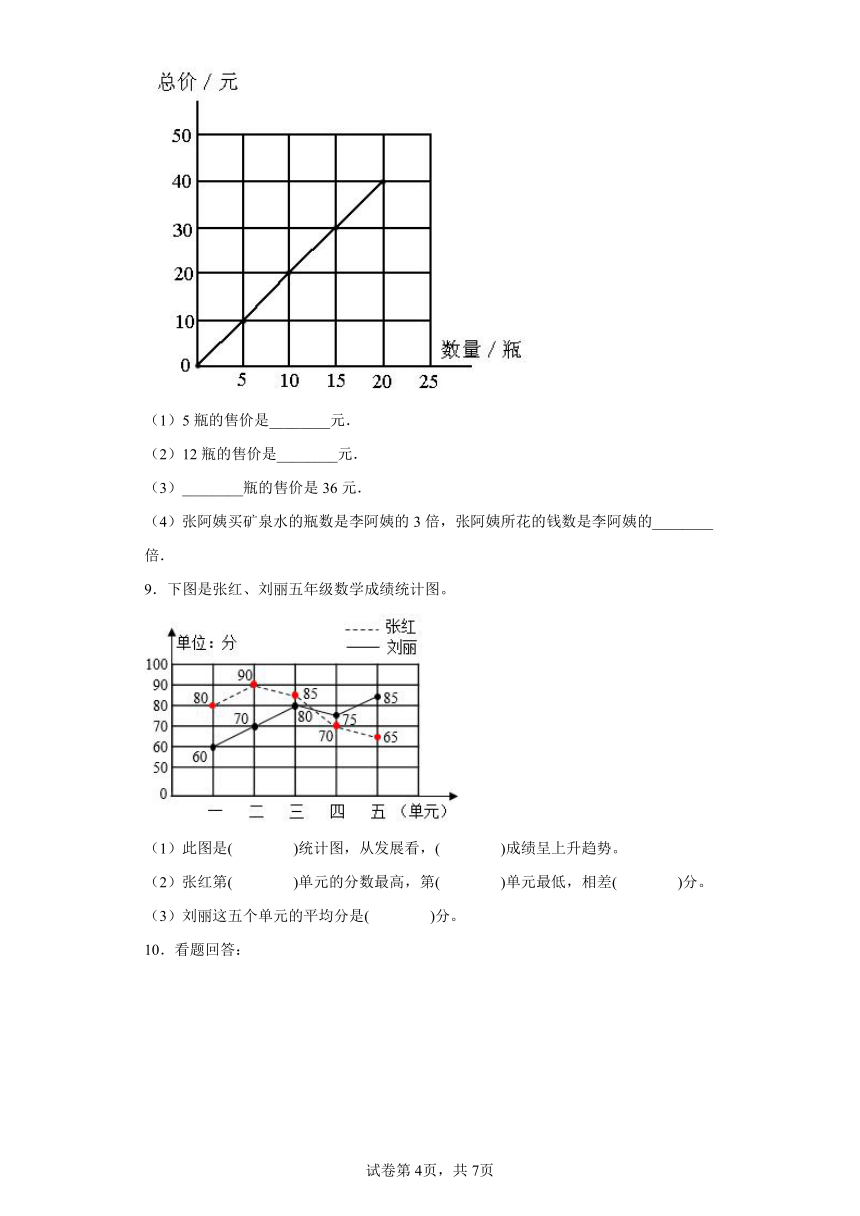
4.医护人员记录一位病人一天的体温变化情况,应选用( ).
A.条形统计图 B.折线统计图
二、填空题
5.娇娇为了解大蒜的初期生长情况,把成瓣大蒜放在装有水的容器里,定时观察,得到蒜芽和根的长度数据如图,由图可知第( )天,芽开始出现;第16-18天,根长了( )mm。
6.为了清楚地表示六年级各班男、女生人数,应选用( )统计图。
7.看图并解答问题。
(1)图中用一个单位长度代表产值( )万元。
(2)把相应的数据填在图中的方框里,食品一厂平均每季度产值( )万元,食品二厂平均每月产值( )万元。
(3)从图上看出,2007年( )厂的总产值较高。
8.下图表示了矿泉水的数量与总价的关系,看图回答问题.
(1)5瓶的售价是________元.
(2)12瓶的售价是________元.
(3)________瓶的售价是36元.
(4)张阿姨买矿泉水的瓶数是李阿姨的3倍,张阿姨所花的钱数是李阿姨的________倍.
9.下图是张红、刘丽五年级数学成绩统计图。
(1)此图是( )统计图,从发展看,( )成绩呈上升趋势。
(2)张红第( )单元的分数最高,第( )单元最低,相差( )分。
(3)刘丽这五个单元的平均分是( )分。
10.看题回答:
①参观博物馆人数最多的年级是________,人数最少的年级是________;
②________年级和________年级参观的人数的和都是600人。
11.绘制统计图示,要清楚地表现出数量的变化趋势应选用( )统计图,只需看出各种数量的多少应选用( )统计图。
12.如图是甲、乙两地2015年上半年每月降水情况统计图。
(1)六月份乙地的降水量比甲地多( )毫米。
(2)甲、乙两地( )月降水量相差最大,相差( )毫米。
13.在2、4、3、3、5、3、5、4、3、5、6、5这组数据中,众数是( )。
14.复式折线统计图和单式折线统计图都有_____共同特点.复式折线统计图相比于单式折线统计图,有______特点.
三、判断题
15.看某地年降水量的变化应绘制单式折线统计图。( )
16.在同一幅条形统计图中,直条越高,表示的数量越多.( )
17.医生要表示病人体温要选用条形统计图表较好。( )
18.要清楚地反映出数量增减变化的统计图是折线统计图. ( )
19.对比两只股票某日的走势情况,应绘制复式折线统计图.( )
20.比较两组数据的增减变化情况,可以绘制复式折线统计图。( )
四、解答题
21.如图①,一个长方形纸条从正方形的左边开始以每秒2厘米的速度沿水平方向向右运动;如图②是运动过程中长方形纸条和正方形重叠部分的面积与运动时间的关系图。
(1)运动4秒后,重叠部分的面积是( )平方厘米。
(2)正方形的边长是( )厘米。
(3)在图②的括号内填入正确的时间。
22.如图是某地区上半年各月份的最高气温统计图。
(1)( )月份的最高气温最高,是( ) ;( )月份的最高气温最低是( )。
(2)( )月份的最高气温比上月份的最高气温增加的最多。
(3)从统计图可以看出,这个地区上半年最高气温的变化呈什么趋势?
23.下表是乙城市蓝天数的统计结果。
年份 2015 2016 2017 2018 2019
蓝天数 310 317 319 310 305
(1)请根据表中数据把统计图补充完整。
(2)甲城市( )年的蓝天数比上一年增加得最多,增加了( )天。
(3)( )年两个城市的蓝天数差距最大。
24.两辆汽车行驶时间与路程的关系如下表。观察其中的规律,填完下表。
时间(小时) 1 2 3 4 5 6 7 8
甲车路程(千米) 60 120 240 300 420
乙车路程(千米) 80 160 320 400 560
根据上表的数据,在下图中绘制复式折线统计图。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
观察统计图发现,斑马20分跑了24千米,长颈鹿30分跑了24千米,根据路程÷时间=速度,可求出斑马和长颈鹿各自的速度。据此解答即可。
【详解】
24÷20-24÷30
=1.2-0.8
=0.4(千米)
斑马比长颈鹿每分钟快0.4千米。
故选:A
【点睛】
本题考查折线统计图,通过统计图分析出相应的数据是解题的关键。
2.B
【解析】
【分析】
由题意可知:每年每户用气(天燃气)量不超过300立方米,每立方米3.45元;即300立方米以内,每立方米天燃气的单价不变,然后水量超过300立方米时,超过的部分每立方米为4.15元,单价变化相对来说幅度变大;据此选择即可。
【详解】
折线统计图中超过300立方米,单价变化相对来说幅度变大;所以能正确表示每年用气费用与用气量关系的示意图是B。
故选B。
【点睛】
此题应根据单价和用天燃气的体积之间的关系进行分析判断。
3.A
【解析】
【详解】
折线统计图A所提供的信息与题中所提供的信息相同;
由折线统计图:A所提供的信息是从学校出发,乘车0.5小时,来到离校5千米的科技馆,参观1小时返回学校;
折线统计图B提供的信息是从学校出发去科技馆,在科技馆玩了1.5小时后乘车回学校;
折线统计图C提供的信息在返回的时间为2.5﹣1.5=1时,与题干不符合;
折线统计图D是从科技馆出发乘车1小时,来到离科技馆5千米的学校,参观1小时返回科技馆,据此解答.
故选A
4.B
【解析】
【详解】
略
5. 8 16
【解析】
【分析】
观察统计图,虚线起始位置是芽开始出现的时间;找到第16天和第18天根的长度,求差即可。
【详解】
96-80=16(毫米)
由图可知第8天,芽开始出现;第16-18天,根长了16mm。
【点睛】
折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。
6.复式条形
【解析】
【分析】
一般来说,如果几个数量是并列的,只要求表示数量的多少时,选条形统计图。如果表示一个量或几个量增减变化和发展变化趋势,则选折线统计图。
【详解】
为了清楚地表示六年级各班男、女生人数,应选用复式条形统计图。
【点睛】
关键是熟悉条形统计图和折线统计图的特点。
7. 5 18.75 二
【解析】
【分析】
(1)由图可知2个单位长度是10万元,由此求出每个单位长度表示的数量;
(2)实线表示一厂的产值,其中第一季度是15万元,第二季度是10万元,第三季度是20万元,第四季度是30万元;
由此在图中标出一厂的产值,然后求出总产值,用总产值除以4就是平均每个季度的产值;
虚线表示二厂的产值,第一季度是15万元,第二季度是20万元,第三季度是30万元,第四季度是35万元;
由此在图中标出二厂的产值,然后求出总产值,用总产值除以12就是平均每个月的产值;
(3)虚线一直在实线的上边,所以二厂的产值较高。
【详解】
(1)10÷2=5(万元);
图中用一个单位长度代表产值5万元。
(2)图如下:
(15+10+20+30)÷4,
=75÷4,
=18.75(万元);
(15+20+30+35)÷12,
=100÷12,
=(万元);
答:食品一厂平均每季度产值18.75万元,食品二厂平均每月产值万元。
(3)从图上看出,2007年二厂的总产值较高。
故答案为5,18.75,;二。
【点睛】
先求出单位长度表示的数量,然后读出数据,再根据基本的数量关系解决问题。
8. 10 24 18 3
【解析】
【分析】
观察数据,总价与瓶数成正比例;(1)根据5瓶对应的钱数判断售价;(2)计算出每瓶的售价,然后用每瓶的售价乘瓶数求出总售价;(3)用总钱数除以每瓶的售价求出瓶数;(4)根据正比例关系的意义判断所花钱数的倍数关系.
【详解】
(1)5瓶对应的钱数是10元,所以5瓶的售价是10元;
(2)10÷5=2(元),12×2=24(元),所以12瓶的售价是24元;
(3)36÷2=18(瓶),18瓶的售价是36元;
(4)因为瓶数与钱数成正比例,所以张阿姨所花的钱数是李阿姨的3倍.
故答案为10;24;18;3
9. 复式折线 刘丽 二 五 25 74
【解析】
【分析】
(1)此图是复式折线统计图,根据统计图可知,表示刘丽数学成绩的折线处于上升趋势,所以刘丽的成绩呈上升趋势,据此解答即可;
(2)统计图中,点越高,表示分数越高,反之则分数较低,找到最低分和最高分,两者作差即可;
(3)将刘丽五个单元的成绩相加,再除以5即可。
【详解】
(1)此图是复式折线统计图,刘丽的成绩呈上升趋势;
(2)张红第二单元的分数最高,第五单元最低;
90-65=25(分);
(3)(60+70+80+75+85)÷5
=370÷5
=74(分)
【点睛】
本题综合性较强,读懂统计图中的数学信息是解答本题的关键。
10. 四年级 五年级 一、二 四、五
【解析】
【详解】
①人数最多的年级是四年级,人数最少的年级是五年级;②200+400=600(人),一年级和二年级参观的人数和是600人;500+100=600(人);四年级和五年级参观的人数和是600人。
【点睛】
本题考查的是折线统计图的应用,解答此题的关键利用已知的信息,以及从图中获取信息的计算能力。
11. 折线 条形
【解析】
【分析】
条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较。折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
【详解】
绘制统计图示,要清楚地表现出数量的变化趋势应选用折线统计图,只需看出各种数量的多少应选用条形统计图。
【点睛】
熟练掌握条形统计图和折线统计图的特点是解决本题的关键。
12. 45 五 210
【解析】
【分析】
由折线统计图可知:(1)甲地六月份的降水量为500毫升,乙地六月份的降水量为545毫升,相减即可求出六月份乙地的降水量比甲地多多少毫升。
(2)甲、乙两地5月份降水量相差最大,降水量分别为355毫升、565毫升;据此解答。
【详解】
(1)六月份乙地的降水量比甲地多545-500=45毫升。
(2)甲、乙两地五月降水量相差最大,相差565-355=210毫米。
故答案为:45;五;210
【点睛】
本题主要考查复式折线统计图的简单应用,解题的关键是正确提取统计图中的数据信息。
13.3和5
【解析】
【分析】
在一组数据中,出现次数最多的数就叫这组数据的众数,如果有两个或两个以上的数出现次数都是最多的,那么这几个数都是这组数据的众数,根据这一特点即可解决问题。
【详解】
在这组数据中,3出现了4次,5出现了4次,4出现了2次,2出现了1次,6出现了1次,所以3和5是这组数据的众数。
【点睛】
此题考查了众数的意义和求解方法。
14. 能够表现量的增减变化情况 能够表现两个量之间差的情况
【解析】
【详解】
略
15.√
【解析】
【分析】
根据折线统计图的特点,可以反映出增减变化趋势,分析即可。
【详解】
看某地年降水量的变化应绘制单式折线统计图,说法正确。
故答案为:√
【点睛】
本题考查了折线统计图的特点,条形统计图便于比较多少。
16.√
【解析】
【分析】
【详解】
解:在同一幅条形统计图中,直条越高,表示的数量越多。
故答案为:正确。
【分析】因为条形统计图的纵轴表示数量的多少,所以直条越高,表示的数量越多。
17.×
【解析】
【分析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】
根据统计图的特点可知:医生需要监测病人的体温情况,应选用折线统计图;
所以原题说法错误。
故答案为:×。
【点睛】
此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
18.正确
【解析】
【详解】
要反映数量的增减变化情况,可以选用折线统计图.
19.√
【解析】
【详解】
复式折线统计图是用不同颜色和线型区别表示两个或多个项目的数量及变化趋势。复式折线图用于对同类数量或相关数量进行比较,有利于对事物的发展变化趋势进行更准确地把握。
故答案为√。
【点睛】
在条形统计图,折线统计图、扇形统计图三者中,折线图更能表示变化的趋势,如果需要表示两个或更多项目的比较,就可以使用复式图。
20.√
【解析】
【分析】
折线统计图可以分为两种,一种是单式折线统计图,一种是复式折线统计图,复式折线统计图与单式折线统计图相比,复式折线统计图不仅能表示每组数据的增减变化情况,而且还便于两组相关数据进行比较;由此解答即可。
【详解】
根据统计图的特点可知:复式折线统计图能清楚地反映两组数据的增减变化情况,而且更便于两组相关数据进行比较。
故答案为:√
【点睛】
本题考查统计图的选择,要掌握不同统计图的不同特点是解答本题的关键。
21.(1)16
(2)12
(3)
【解析】
【分析】
在表示路程和时间的行程问题的折线统计图中,折线上升,表示向目的地运动;折线呈水平方向,表示在某地停留,折线下降,表示向出发地运动。据此可解答。
(1)运动4秒,运动的长是2×4=8(厘米),宽是2厘米,重叠部分的面积是长方形8×2=16(平方厘米),据此可解答。
(2)根据题意看图,第6秒以后,重叠部分开始不变,即正方形的边长是6×2=12(厘米),据此解答即可。
(3)当长方形的左端,刚好穿过正方形时,还需要8+2=10(秒)。所以第一个括号填10。
长方形的左端完全离开正方形,相当于火车行程间题,(20+12) +2=16(秒)
所以第二个括号填16,没有重叠部分,面积为0。
【详解】
(1)8×2=16(平方厘米)
(2)6×2=12(厘米)
(3)
【点睛】
这里有行程问题,折线统计图问题,通过折线统计图分析长方形纸条和正方形重叠部分的面积与运动时间是解题的关键。
22.见详解
【解析】
【分析】
(1)通过观察统计图可知,6月份的最高气温最高,是30,1月份的最高气温最低,是5。
(2)4月份的最高气温比3月份的最高气温增加的最多。
(3)从统计图可以看出,这个地区上半年最高气温的变化呈上升趋势。据此解答。
【详解】
(1)6月份的最高气温最高,是30,1月份的最高气温最低,是5。
(2)4月份的最高气温比3月份的最高气温增加的最多。
(3)从统计图可以看出,这个地区上半年最高气温的变化呈上升趋势。
【点睛】
此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
23.(1)见详解;(2)2018;15;(3)2017
【解析】
【分析】
(1)根据统计表中的数据,先找乙城市2015——2019年蓝天数并描点,然后用虚线连起来;
(2)根据统计图中的数据解答;
(3)观察统计图,实线和虚线相差最大的那一年即是两个城市的蓝天数差距最大的年份。
【详解】
(1)甲、乙两个城市2015—2019年蓝天数统计图
(2)312-197=15(天)
甲城市(2018)年的蓝天数比上一年增加得最多,增加了(15)天。
(3)2017年两个城市的蓝天数差距最大。
【点睛】
此题主要考查的是复式折线统计图的相关知识,要认真审题,会读取统计图的数据,会计算有关的问题。
24.(1)统计表如下:
时间(小时) 1 2 3 4 5 6 7 8
甲车路程(千米) 60 120 180 240 300 360 420 480
乙车路程(千米) 80 160 240 320 400 480 560 640
(2)绘制复式统计图如下:
【解析】
【分析】
观察统计表中前两组数据,根据路程÷时间=速度,表中甲乙的速度不变,所以时间对应的路程=速度×时间。依此填写完整统计表。绘制复式统计图时,横轴表示时间,纵轴上数据表示的是路程,根据所行的时间对应的路程多少描出各点,然后把各点用线段顺次连接起来。复式的折线统计图有图例,用不同形状的线条区别开来,实线表示甲车行驶的路程,虚线表示乙车行驶的路程。
【详解】
(1)甲的速度:60÷1=60(千米/小时),
3小时行驶的路程是:60×3=180(千米),
6小时行驶的路程是:60×6=360(千米),
8小时行驶的路程是:60×8=480(千米);
乙的速度:80÷1=80(千米/小时),
3小时行驶的路程是:80×3=240(千米),
6小时行驶的路程是:80×6=480(千米),
8小时行驶的路程是:80×8=640(千米);
统计表如下:
时间(小时) 1 2 3 4 5 6 7 8
甲车路程(千米) 60 120 180 240 300 360 420 480
乙车路程(千米) 80 160 240 320 400 480 560 640
(2)根据统计表,绘制的统计图如下:
【点睛】
此题主要考查会观察统计表数据,熟练掌握复式的折线统计图的绘制方法。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.观察图中斑马和长颈鹿的奔跑情况,斑马比长颈鹿每分钟快( )千米。
A.0.4 B.0.8 C.4 D.8
2.珠海市规定:每年每户用气(天燃气)量不超过300立方米,每立方米3.45元;当用气量超过300立方米时,超过的部分每立方米为4.15元。下图中能正确表示每年用气费用与用气量关系的示意图是( )
A. B. C.
3.育才小学六年级同学从学校出发,乘车0.5时,来到离学校5千米远的科技馆,参观1时,出馆后休息0.5时,然后乘车0.5时返回学校.下面四幅图中,描述了育才小学六年级同学这一活动行程的是图( )
A. B.
C. D.
4.医护人员记录一位病人一天的体温变化情况,应选用( ).
A.条形统计图 B.折线统计图
二、填空题
5.娇娇为了解大蒜的初期生长情况,把成瓣大蒜放在装有水的容器里,定时观察,得到蒜芽和根的长度数据如图,由图可知第( )天,芽开始出现;第16-18天,根长了( )mm。
6.为了清楚地表示六年级各班男、女生人数,应选用( )统计图。
7.看图并解答问题。
(1)图中用一个单位长度代表产值( )万元。
(2)把相应的数据填在图中的方框里,食品一厂平均每季度产值( )万元,食品二厂平均每月产值( )万元。
(3)从图上看出,2007年( )厂的总产值较高。
8.下图表示了矿泉水的数量与总价的关系,看图回答问题.
(1)5瓶的售价是________元.
(2)12瓶的售价是________元.
(3)________瓶的售价是36元.
(4)张阿姨买矿泉水的瓶数是李阿姨的3倍,张阿姨所花的钱数是李阿姨的________倍.
9.下图是张红、刘丽五年级数学成绩统计图。
(1)此图是( )统计图,从发展看,( )成绩呈上升趋势。
(2)张红第( )单元的分数最高,第( )单元最低,相差( )分。
(3)刘丽这五个单元的平均分是( )分。
10.看题回答:
①参观博物馆人数最多的年级是________,人数最少的年级是________;
②________年级和________年级参观的人数的和都是600人。
11.绘制统计图示,要清楚地表现出数量的变化趋势应选用( )统计图,只需看出各种数量的多少应选用( )统计图。
12.如图是甲、乙两地2015年上半年每月降水情况统计图。
(1)六月份乙地的降水量比甲地多( )毫米。
(2)甲、乙两地( )月降水量相差最大,相差( )毫米。
13.在2、4、3、3、5、3、5、4、3、5、6、5这组数据中,众数是( )。
14.复式折线统计图和单式折线统计图都有_____共同特点.复式折线统计图相比于单式折线统计图,有______特点.
三、判断题
15.看某地年降水量的变化应绘制单式折线统计图。( )
16.在同一幅条形统计图中,直条越高,表示的数量越多.( )
17.医生要表示病人体温要选用条形统计图表较好。( )
18.要清楚地反映出数量增减变化的统计图是折线统计图. ( )
19.对比两只股票某日的走势情况,应绘制复式折线统计图.( )
20.比较两组数据的增减变化情况,可以绘制复式折线统计图。( )
四、解答题
21.如图①,一个长方形纸条从正方形的左边开始以每秒2厘米的速度沿水平方向向右运动;如图②是运动过程中长方形纸条和正方形重叠部分的面积与运动时间的关系图。
(1)运动4秒后,重叠部分的面积是( )平方厘米。
(2)正方形的边长是( )厘米。
(3)在图②的括号内填入正确的时间。
22.如图是某地区上半年各月份的最高气温统计图。
(1)( )月份的最高气温最高,是( ) ;( )月份的最高气温最低是( )。
(2)( )月份的最高气温比上月份的最高气温增加的最多。
(3)从统计图可以看出,这个地区上半年最高气温的变化呈什么趋势?
23.下表是乙城市蓝天数的统计结果。
年份 2015 2016 2017 2018 2019
蓝天数 310 317 319 310 305
(1)请根据表中数据把统计图补充完整。
(2)甲城市( )年的蓝天数比上一年增加得最多,增加了( )天。
(3)( )年两个城市的蓝天数差距最大。
24.两辆汽车行驶时间与路程的关系如下表。观察其中的规律,填完下表。
时间(小时) 1 2 3 4 5 6 7 8
甲车路程(千米) 60 120 240 300 420
乙车路程(千米) 80 160 320 400 560
根据上表的数据,在下图中绘制复式折线统计图。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
观察统计图发现,斑马20分跑了24千米,长颈鹿30分跑了24千米,根据路程÷时间=速度,可求出斑马和长颈鹿各自的速度。据此解答即可。
【详解】
24÷20-24÷30
=1.2-0.8
=0.4(千米)
斑马比长颈鹿每分钟快0.4千米。
故选:A
【点睛】
本题考查折线统计图,通过统计图分析出相应的数据是解题的关键。
2.B
【解析】
【分析】
由题意可知:每年每户用气(天燃气)量不超过300立方米,每立方米3.45元;即300立方米以内,每立方米天燃气的单价不变,然后水量超过300立方米时,超过的部分每立方米为4.15元,单价变化相对来说幅度变大;据此选择即可。
【详解】
折线统计图中超过300立方米,单价变化相对来说幅度变大;所以能正确表示每年用气费用与用气量关系的示意图是B。
故选B。
【点睛】
此题应根据单价和用天燃气的体积之间的关系进行分析判断。
3.A
【解析】
【详解】
折线统计图A所提供的信息与题中所提供的信息相同;
由折线统计图:A所提供的信息是从学校出发,乘车0.5小时,来到离校5千米的科技馆,参观1小时返回学校;
折线统计图B提供的信息是从学校出发去科技馆,在科技馆玩了1.5小时后乘车回学校;
折线统计图C提供的信息在返回的时间为2.5﹣1.5=1时,与题干不符合;
折线统计图D是从科技馆出发乘车1小时,来到离科技馆5千米的学校,参观1小时返回科技馆,据此解答.
故选A
4.B
【解析】
【详解】
略
5. 8 16
【解析】
【分析】
观察统计图,虚线起始位置是芽开始出现的时间;找到第16天和第18天根的长度,求差即可。
【详解】
96-80=16(毫米)
由图可知第8天,芽开始出现;第16-18天,根长了16mm。
【点睛】
折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。
6.复式条形
【解析】
【分析】
一般来说,如果几个数量是并列的,只要求表示数量的多少时,选条形统计图。如果表示一个量或几个量增减变化和发展变化趋势,则选折线统计图。
【详解】
为了清楚地表示六年级各班男、女生人数,应选用复式条形统计图。
【点睛】
关键是熟悉条形统计图和折线统计图的特点。
7. 5 18.75 二
【解析】
【分析】
(1)由图可知2个单位长度是10万元,由此求出每个单位长度表示的数量;
(2)实线表示一厂的产值,其中第一季度是15万元,第二季度是10万元,第三季度是20万元,第四季度是30万元;
由此在图中标出一厂的产值,然后求出总产值,用总产值除以4就是平均每个季度的产值;
虚线表示二厂的产值,第一季度是15万元,第二季度是20万元,第三季度是30万元,第四季度是35万元;
由此在图中标出二厂的产值,然后求出总产值,用总产值除以12就是平均每个月的产值;
(3)虚线一直在实线的上边,所以二厂的产值较高。
【详解】
(1)10÷2=5(万元);
图中用一个单位长度代表产值5万元。
(2)图如下:
(15+10+20+30)÷4,
=75÷4,
=18.75(万元);
(15+20+30+35)÷12,
=100÷12,
=(万元);
答:食品一厂平均每季度产值18.75万元,食品二厂平均每月产值万元。
(3)从图上看出,2007年二厂的总产值较高。
故答案为5,18.75,;二。
【点睛】
先求出单位长度表示的数量,然后读出数据,再根据基本的数量关系解决问题。
8. 10 24 18 3
【解析】
【分析】
观察数据,总价与瓶数成正比例;(1)根据5瓶对应的钱数判断售价;(2)计算出每瓶的售价,然后用每瓶的售价乘瓶数求出总售价;(3)用总钱数除以每瓶的售价求出瓶数;(4)根据正比例关系的意义判断所花钱数的倍数关系.
【详解】
(1)5瓶对应的钱数是10元,所以5瓶的售价是10元;
(2)10÷5=2(元),12×2=24(元),所以12瓶的售价是24元;
(3)36÷2=18(瓶),18瓶的售价是36元;
(4)因为瓶数与钱数成正比例,所以张阿姨所花的钱数是李阿姨的3倍.
故答案为10;24;18;3
9. 复式折线 刘丽 二 五 25 74
【解析】
【分析】
(1)此图是复式折线统计图,根据统计图可知,表示刘丽数学成绩的折线处于上升趋势,所以刘丽的成绩呈上升趋势,据此解答即可;
(2)统计图中,点越高,表示分数越高,反之则分数较低,找到最低分和最高分,两者作差即可;
(3)将刘丽五个单元的成绩相加,再除以5即可。
【详解】
(1)此图是复式折线统计图,刘丽的成绩呈上升趋势;
(2)张红第二单元的分数最高,第五单元最低;
90-65=25(分);
(3)(60+70+80+75+85)÷5
=370÷5
=74(分)
【点睛】
本题综合性较强,读懂统计图中的数学信息是解答本题的关键。
10. 四年级 五年级 一、二 四、五
【解析】
【详解】
①人数最多的年级是四年级,人数最少的年级是五年级;②200+400=600(人),一年级和二年级参观的人数和是600人;500+100=600(人);四年级和五年级参观的人数和是600人。
【点睛】
本题考查的是折线统计图的应用,解答此题的关键利用已知的信息,以及从图中获取信息的计算能力。
11. 折线 条形
【解析】
【分析】
条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较。折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
【详解】
绘制统计图示,要清楚地表现出数量的变化趋势应选用折线统计图,只需看出各种数量的多少应选用条形统计图。
【点睛】
熟练掌握条形统计图和折线统计图的特点是解决本题的关键。
12. 45 五 210
【解析】
【分析】
由折线统计图可知:(1)甲地六月份的降水量为500毫升,乙地六月份的降水量为545毫升,相减即可求出六月份乙地的降水量比甲地多多少毫升。
(2)甲、乙两地5月份降水量相差最大,降水量分别为355毫升、565毫升;据此解答。
【详解】
(1)六月份乙地的降水量比甲地多545-500=45毫升。
(2)甲、乙两地五月降水量相差最大,相差565-355=210毫米。
故答案为:45;五;210
【点睛】
本题主要考查复式折线统计图的简单应用,解题的关键是正确提取统计图中的数据信息。
13.3和5
【解析】
【分析】
在一组数据中,出现次数最多的数就叫这组数据的众数,如果有两个或两个以上的数出现次数都是最多的,那么这几个数都是这组数据的众数,根据这一特点即可解决问题。
【详解】
在这组数据中,3出现了4次,5出现了4次,4出现了2次,2出现了1次,6出现了1次,所以3和5是这组数据的众数。
【点睛】
此题考查了众数的意义和求解方法。
14. 能够表现量的增减变化情况 能够表现两个量之间差的情况
【解析】
【详解】
略
15.√
【解析】
【分析】
根据折线统计图的特点,可以反映出增减变化趋势,分析即可。
【详解】
看某地年降水量的变化应绘制单式折线统计图,说法正确。
故答案为:√
【点睛】
本题考查了折线统计图的特点,条形统计图便于比较多少。
16.√
【解析】
【分析】
【详解】
解:在同一幅条形统计图中,直条越高,表示的数量越多。
故答案为:正确。
【分析】因为条形统计图的纵轴表示数量的多少,所以直条越高,表示的数量越多。
17.×
【解析】
【分析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】
根据统计图的特点可知:医生需要监测病人的体温情况,应选用折线统计图;
所以原题说法错误。
故答案为:×。
【点睛】
此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
18.正确
【解析】
【详解】
要反映数量的增减变化情况,可以选用折线统计图.
19.√
【解析】
【详解】
复式折线统计图是用不同颜色和线型区别表示两个或多个项目的数量及变化趋势。复式折线图用于对同类数量或相关数量进行比较,有利于对事物的发展变化趋势进行更准确地把握。
故答案为√。
【点睛】
在条形统计图,折线统计图、扇形统计图三者中,折线图更能表示变化的趋势,如果需要表示两个或更多项目的比较,就可以使用复式图。
20.√
【解析】
【分析】
折线统计图可以分为两种,一种是单式折线统计图,一种是复式折线统计图,复式折线统计图与单式折线统计图相比,复式折线统计图不仅能表示每组数据的增减变化情况,而且还便于两组相关数据进行比较;由此解答即可。
【详解】
根据统计图的特点可知:复式折线统计图能清楚地反映两组数据的增减变化情况,而且更便于两组相关数据进行比较。
故答案为:√
【点睛】
本题考查统计图的选择,要掌握不同统计图的不同特点是解答本题的关键。
21.(1)16
(2)12
(3)
【解析】
【分析】
在表示路程和时间的行程问题的折线统计图中,折线上升,表示向目的地运动;折线呈水平方向,表示在某地停留,折线下降,表示向出发地运动。据此可解答。
(1)运动4秒,运动的长是2×4=8(厘米),宽是2厘米,重叠部分的面积是长方形8×2=16(平方厘米),据此可解答。
(2)根据题意看图,第6秒以后,重叠部分开始不变,即正方形的边长是6×2=12(厘米),据此解答即可。
(3)当长方形的左端,刚好穿过正方形时,还需要8+2=10(秒)。所以第一个括号填10。
长方形的左端完全离开正方形,相当于火车行程间题,(20+12) +2=16(秒)
所以第二个括号填16,没有重叠部分,面积为0。
【详解】
(1)8×2=16(平方厘米)
(2)6×2=12(厘米)
(3)
【点睛】
这里有行程问题,折线统计图问题,通过折线统计图分析长方形纸条和正方形重叠部分的面积与运动时间是解题的关键。
22.见详解
【解析】
【分析】
(1)通过观察统计图可知,6月份的最高气温最高,是30,1月份的最高气温最低,是5。
(2)4月份的最高气温比3月份的最高气温增加的最多。
(3)从统计图可以看出,这个地区上半年最高气温的变化呈上升趋势。据此解答。
【详解】
(1)6月份的最高气温最高,是30,1月份的最高气温最低,是5。
(2)4月份的最高气温比3月份的最高气温增加的最多。
(3)从统计图可以看出,这个地区上半年最高气温的变化呈上升趋势。
【点睛】
此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
23.(1)见详解;(2)2018;15;(3)2017
【解析】
【分析】
(1)根据统计表中的数据,先找乙城市2015——2019年蓝天数并描点,然后用虚线连起来;
(2)根据统计图中的数据解答;
(3)观察统计图,实线和虚线相差最大的那一年即是两个城市的蓝天数差距最大的年份。
【详解】
(1)甲、乙两个城市2015—2019年蓝天数统计图
(2)312-197=15(天)
甲城市(2018)年的蓝天数比上一年增加得最多,增加了(15)天。
(3)2017年两个城市的蓝天数差距最大。
【点睛】
此题主要考查的是复式折线统计图的相关知识,要认真审题,会读取统计图的数据,会计算有关的问题。
24.(1)统计表如下:
时间(小时) 1 2 3 4 5 6 7 8
甲车路程(千米) 60 120 180 240 300 360 420 480
乙车路程(千米) 80 160 240 320 400 480 560 640
(2)绘制复式统计图如下:
【解析】
【分析】
观察统计表中前两组数据,根据路程÷时间=速度,表中甲乙的速度不变,所以时间对应的路程=速度×时间。依此填写完整统计表。绘制复式统计图时,横轴表示时间,纵轴上数据表示的是路程,根据所行的时间对应的路程多少描出各点,然后把各点用线段顺次连接起来。复式的折线统计图有图例,用不同形状的线条区别开来,实线表示甲车行驶的路程,虚线表示乙车行驶的路程。
【详解】
(1)甲的速度:60÷1=60(千米/小时),
3小时行驶的路程是:60×3=180(千米),
6小时行驶的路程是:60×6=360(千米),
8小时行驶的路程是:60×8=480(千米);
乙的速度:80÷1=80(千米/小时),
3小时行驶的路程是:80×3=240(千米),
6小时行驶的路程是:80×6=480(千米),
8小时行驶的路程是:80×8=640(千米);
统计表如下:
时间(小时) 1 2 3 4 5 6 7 8
甲车路程(千米) 60 120 180 240 300 360 420 480
乙车路程(千米) 80 160 240 320 400 480 560 640
(2)根据统计表,绘制的统计图如下:
【点睛】
此题主要考查会观察统计表数据,熟练掌握复式的折线统计图的绘制方法。
答案第1页,共2页
答案第1页,共2页
