人教版数学五年级下册第四单元《分数的意义和性质》目标检测卷(含答案)
文档属性
| 名称 | 人教版数学五年级下册第四单元《分数的意义和性质》目标检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 286.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 07:15:31 | ||
图片预览




文档简介
人教版数学五年级下册第四单元《分数的意义和性质》目标检测卷
一、选择题
1.小时是( )分钟。
A.15 B.12 C.20 D.25
2.把吨煤平均分成4份,每份是1吨的( )
A. B. C. D.
3.甲队6天修路48千米,乙队4天修路24千米。甲队6天修的路乙队需要多少天?下面列式正确的是( )。
A.24÷4×6 B.48÷6×4 C.48÷(24÷4)
4.一个最简分数,如果分母中只含有因数(),再无其他因数,那么这个分数可以化成有限小数;否则就不能化成有限小数.
A.2 和3 B.3 C.3和 5 D.2和5
5.下列分数中,能化成有限小数的是( )
A. B. C.
6.下面各数中,不能化成有限小数的是( )。
A. B. C. D.
7.两根同样长的绳子,第一根剪去,第二根剪去米,第一根余下的比第二根余下的长.那么每根绳长( )
A.比1米长 B.比1米短 C.等于1米
二、其他计算
8.分数和小数互化。
0.15= (保留两位小数)≈
9.把下面的分数约分,是假分数的要化成带分数或整数。
= = =
10.将下面的假分数化成带分数或整数。
= = = =
11.把下面的假分数化成带分数。
= = =
12.求下列各组数的最大公因数和最小公倍数。
15和16 29和87 24和64
三、填空题
13.有一个最简分数,把分子加上分母,分母也加上分母,所得到的新分数是原分数的9倍,这个最简分数是 .
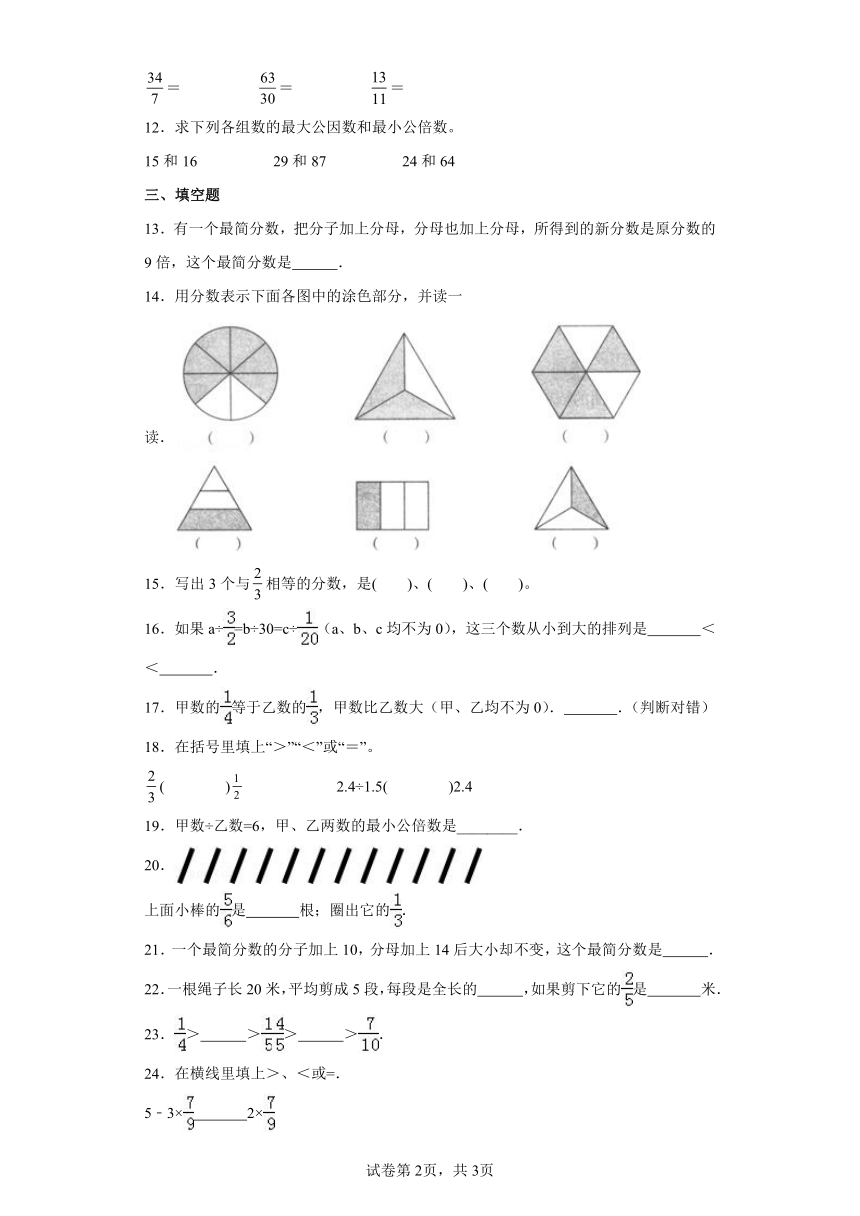
14.用分数表示下面各图中的涂色部分,并读一读.
15.写出3个与相等的分数,是( )、( )、( )。
16.如果a÷=b÷30=c÷(a、b、c均不为0),这三个数从小到大的排列是 < < .
17.甲数的等于乙数的,甲数比乙数大(甲、乙均不为0). .(判断对错)
18.在括号里填上“>”“<”或“=”。
( ) 2.4÷1.5( )2.4
19.甲数÷乙数=6,甲、乙两数的最小公倍数是________.
20.
上面小棒的是 根;圈出它的.
21.一个最简分数的分子加上10,分母加上14后大小却不变,这个最简分数是 .
22.一根绳子长20米,平均剪成5段,每段是全长的 ,如果剪下它的是 米.
23.> >> >.
24.在横线里填上>、<或=.
5﹣3× 2×
÷+÷ (+)÷.
25.一份稿件,甲单独用计算机录入要用8小时,乙单独用计算机录入要用10小时.
(1)甲先录入3小时,剩下的由乙录入,还要用_____小时.
(2)甲先录入3小时,余下的两人合作,还要_____小时.
(3)甲、乙合作录入3小时,剩下的由甲单独录入.还要_____小时.
(带分数,先填写整数部分,再填写分子部分,最后填写分母部分)
26.把一条3分米长的纸条对折再对折,对折后每段的长度是全长的 ,每段长________分米.
四、判断题
27.和相等的分数有无数个. ___
28.如果两个数的最大因数是1,那么这两数的最小公倍数就是它们的乘积。( )
29.一根铁丝分成6段,每段是这根铁丝的。( )
30.既是6的倍数又是8的倍数的数只有48. .
31.把一个蛋糕分成8份,每份是这个蛋糕的。( )
32.梨树棵数的相当于苹果树棵数,是把苹果树棵数看作单位“1”.( )
五、解答题
33.将下列各分数化成最简分数.
,,.
34.小明13分钟画了7辆小汽车,小强8分钟画了5辆小汽车,谁的画画速度比较快?
35.一批货物,第一天运走它的,第二天运走它的,第三天运走它的.哪天运走的最多?哪天运走的最少?
36.有一串彩球,按1个红球、2个白球就、3个黄球的规律排列,这串彩球共80个.三种颜色的求各占总数的几分之几?
37.三(6)班手工兴趣小组的15名学生做了3件手工作品。照这样计算,兴趣小组有40名学生,一共可以做几件手工作品?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
1小时是60分钟,小时也就是60分钟的,把60分钟平均分成4份,取走1份即可。
【详解】
1小时是60分钟,60分钟的是15分钟;
故答案选:A。
【点睛】
化成小数是0.25,大单位化小单位乘进率,0.25乘60,得到15分钟。
2.A
【解析】
【详解】
试题分析:根据分数的意义,把吨煤平均分成4份,每份就是这“吨煤”的,所以每份重×=吨.同理,吨也就是1吨煤的.
解:×=(吨)
所以把吨煤平均分成4份,每份是1吨的;
故选A.
【点评】本题重点考查了分数的意义.
3.C
【解析】
【分析】
首先根据:工作效率=工作量÷工作时间,用乙队修路的长度除以用的时间,求出乙队每天修路多少千米;然后用甲队6天修路的长度除以乙队每天修路的长度,求出甲队6天修的路乙队需要多少天即可。
【详解】
48÷(24÷4)
=48÷6
=8(天)
故答案为:C
【点睛】
此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率。
4.D
【解析】
【详解】
分母中只有2、5因子的分数,它们总可以把2和5一个配一个相乘而成一个个的10连乘(缺多少2或5就可以根据分数的性质给分子分母同乘而补足),结果分母总能成了100......00型,这样的分数当然就能化成有限小数了.
故选D
此题主要考察分数和小数的互化
5.C
【解析】
【详解】
试题分析:首先,要把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
解:的分母中含有质因数3,所以不能化成有限小数;
的分母中含有质因数3,所以不能化成有限小数;
化简后是,分母中只有质因数5,所以能化成有限小数.
故选C.
【点评】此题主要考查什么样的分数可以化成有限小数,根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.就能很快判断出什么样的分数能化成有限小数,什么样的分数不能化成有限小数.
6.A
【解析】
【分析】
分数化为小数,直接用分子除以分母,据此将每个选项中的分数都互为小数,再进行判断选择即可。
【详解】
A.≈0.83;
B.=0.25;
C.=0.3125;
D.=0.375;
故答案为:A。
【点睛】
熟练掌握分数与小数的互化方法是解答本题的关键。
7.B
【解析】
【详解】
试题分析:一个数乘上大于1的数,积大于这个数;一个数乘上1,积等于这个数;一个数乘上小于1的数,积小于这个数,据此解答.
解:因两根同样长的绳子,第一根剪去,第二根剪去米,
(1)当绳子长度大于1米时,乘上的绳子长度大于米,用去的比第二根多,剩下的绳子就比第二根剩下的短;
(2)当绳子长度等于1米时,乘上绳子的长度等于米,用去的和第二根一样长,剩下的绳子就和第二根剩下的一样长;
(3)当绳子长度小于1米时,乘上绳子的长度小于米,用去的比第二根少,剩下的绳子就比第二根剩下的长.
故选B.
点评:本题考查了学生对于一个数同另一个数相乘,积与这个数大小知识情况的掌握.
8.0.36;;0.53
【解析】
【分析】
分数化成小数,分子除以分母,商用小数表示;小数化成分数,原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分,据此解答。
【详解】
9÷25=0.36;0.15= = ;≈0.53
【点睛】
此题考查了分数、小数的互化,掌握方法,认真计算即可。
9.;1;5
【解析】
【分析】
首先根据约分的方法,把下面各分数进行约分,再根据假分数化成带分数的方法:把假分数化成带分数,用分子除以分母得到的商作整数部分,余数作分子,分母不变,能整除的可以化成整数;据此解答。
【详解】
==
===1
===5
10.1;;;
【解析】
【分析】
假分数化成带分数或整数需要注意:假分数化成整数或者带分数时,假分数的分子除以分母,能整除的,所得的商就是整数;当不能整除时,所得的商就是带分数的整数部分,余数是分数部分的分子,分母不变。
【详解】
5÷5=1;所以=1;
9÷8=1……1;所以=;
15÷13=1……2;所以=;
9÷2=4……1;所以=
【点睛】
根据假分数化成带分数或整数的方法细心解答即可。
11.4;2;1
【解析】
【分析】
假分数化整数或带分数的方法是用分子除以分母,商为整数部分,余数作分子,分母不变。
【详解】
=4;
=2=2;
=1。
12.15和16的最大公因数是1,最小公倍数是240
29和87的最大公因数是29,最小公倍数是87
24和64的最大公因数是8,最小公倍数是192
【解析】
【分析】
对于两个数来说:两个数的公有质因数连乘积是最大公因数,两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数,由此解决问题即可。
【详解】
(1)15和16互质,
15和16的最大公因数是1,最小公倍数是15×16=240。
(2)29和87成倍数关系,
所以29和87的最大公因数是29,最小公倍数是87。
(3)24和64
24=2×2×2×3,64=2×2×2×2×2×2,
24和64的最大公因数是2×2×2=8,最小公倍数是2×2×2×2×2×2×3=192。
【点睛】
如果两个数互质,它们的最大公因数是1,这两个数的积就是它们的最小公倍数;如果两个数成倍数关系,较小的数就是这两个数的最大公因数,较大的数就是这两个数的最小公倍数。如果数据较大则用短除法的形式求。
13.
【解析】
【详解】
试题分析:根据题意,设原分数的分子为,则有:,由此解答.
解:设原分数的分子为,
则有:,
,
,
b+a=18b,
a=17b;
所以.
答:这个最简分数是.
故答案为.
点评:此题主要考查最简分数的意义,根据题意列方程解答比较简便.
14.
【解析】
【详解】
试题分析:分数的意义为:把单位“1”平均分成若干份,表示其中这样一份或几份的数叫分数.据此解答即可.
解:
因为图4,不是平均分成三份,所以阴影不可以用分数表示.
点评:明确分数的意义,是解答此题的关键.
15.
【解析】
【分析】
根据分数的基本性质,分数的分子和分母同时扩大或缩小,分数的大小不变。
【详解】
(1)==
(2)==
(3)==
答案不唯一。
【点睛】
本题考查分数的基本性质,只要分子和分母同时乘以2、3、4就能得到3个分数。
16.b、a、c
【解析】
【详解】
试题分析:先利用除以一个数,就等于乘这个数的倒数,将原式进行变形,再化成同分母分数比较出三个分数的大小,最后依据“积一定的情况下,一个因数大,另一个因数就小”的规律,即可求出三个数的大小.
解:因为a÷=b÷30=c÷,
即a×=b×=c×20,
又因=,20=,
且<<,
所以b<a<c;
故答案为b、a、c.
点评:此题主要考查同分母分数大小比较的方法,以及积一定的情况下,因数的变化规律.
17.正确
【解析】
【详解】
试题分析:由题意知:甲数×=乙数×,根据比例的性质求出甲乙两数的比,即可比较出两数的大小.
解:由题意知:甲数×=乙数×,
甲数:乙数=:=×4=4:3,
可知甲数比乙数大.
故答案为正确.
点评:本题主要考查学生灵活运用比例的性质求出比,进而进行两数的大小比较.
18. > <
【解析】
【分析】
①可先找到两个分数的最小公分母,把两个分数通分,再比较大小即可;
②可根据商与被除数的关系,结合具体数值,进行大小比较。
【详解】
①==
==
因为>
所以>
②1.5>1,根据一个非零数除以一个大于1的数,商小于它本身可得:2.4÷1.5<2.4。
【点睛】
本题应用了通分,以及商与被除数的关系来解答,通分时找最小公分母会使运算较为简便。
19.甲数
【解析】
【详解】
略
20.10
【解析】
【详解】
试题分析:由图可知,图中共有12根据小棒,根据分数的意义,这些小棒的即将这些小棒平均分成6份,取其中的5份,12×=10根,其是将这些小棒平均分成3份,取其中的1份,即12×=4根.
解:12×=10(根);
即面小棒的是10根.
12×=4(根),如图:
故答案为10.
点评:本题的知识点:(1)求一个数的几分之几是多少,用乘法;(2)分数的意义.
21.
【解析】
【详解】
试题分析:分子增加10,那么10是原来分子的倍数;分母增加14,14是原来分母的倍数;而且这两个倍数相同,把10和14分解质因数,找出10和14的最大公约数就是这个倍数,10和14除以这个倍数就是原来分子和分母,进而写出这个分数.
解:10=2×5,
14=2×7;
10和14的最大公约数是2,10是原来分子的2倍,14是原来分母的2倍;
10÷2=5,
14÷2=7;
原来的分数是.
故答案为.
点评:本题也可以设原来的分数是,分子和分母增加后的分数是,根据分数大小不变列出方程,求出x和y的最简整数比即可求解.
22.,8
【解析】
【详解】
试题分析:一根绳子长20米,平均剪成5段,根据分数的意义,即将这根绳子全长当做单位“1”平均分成5份,则每份是全长的1÷5=;它的是20×=8(米).
解:每份是全长的:1÷5=;
它的是:20×=8(米).
故答案为,8.
点评:完成本题的依据为分数的意义:将单位“1”平均分成若干份,表示这样一份或几份的数为分数.
23.,
【解析】
【详解】
试题分析:把、,分别化成同分母的分数,再进行填空即可.
解:因为:,,
所以大于小于,
即,>.
因为:,,
所以>.
故答案为,.
点评:本题运用通分的方法进行解答即可.
24.>,=
【解析】
【详解】
试题分析:(1)可根据分数乘法与除法的运算法则有四则混合运算的运算顺序分别计算出两边算式的结果后进行比较.
(2)可根据乘法分配律进行分析比较.
解:(1)5﹣3×
=5﹣,
=;
2×=;
,
则5﹣3×>2×.
(2)÷+
=×+×
=(+).
(+)÷
=(+)×.
则÷+÷=(+)÷.
故答案为>,=.
点评:完成本题要认真分析计算两边的算式中的数据,然后做出正确的判断.
25. 6 2 2
【解析】
【分析】
不知道工作总量具体是多少,将工作总量看作是单位“1”.可求出甲的工作效率是,乙的工作效率是,两个人合作的工作效率为.
(1)甲录入3小时,剩下的工作总量为1﹣×3=,求乙的工作时间,用剩下的工作总量除以乙的工作效率即可.
(2)甲录入3小时,剩下的工作总量为1﹣×3=,求合作的工作时间,用剩下的工作总量除以合作的工作效率即可.
(3)甲、乙合作录入3小时,剩下的工作总量为1﹣×3=,求甲的工作时间,用剩下的工作总量除以甲的工作效率即可.
【详解】
(1)1÷8=
1÷10=
1﹣×3=
÷=6(小时)
(2)=
1﹣×3=
÷=2(小时)
(3)1﹣×3=
÷=2(小时)
故答案为:6;2;2.
【点睛】
本题考查工程问题需要注意:
①工程问题三个基本量之间的关系,即工作总量=工作效率×工作时间.
②当不知道工作总量具体是多少时,把工作总量看作是单位“1”.
③合作的工作效率等于工作效率的和.
26.
【解析】
【详解】
略
27.√
【解析】
【分析】
本题运用分数的大小比较进行解答,只要分母是分子的2倍的分数都与相等,因此这样的分数有无数个,所以本题的说法是正确的.
【详解】
分母是分子2倍的分数有:、、、…这样的分数有无数个且最简分数值是,
所以本题说法是正确的.
28.√
【解析】
【分析】
求两个数的最小公倍数,要看两个数之间的关系:两个数互质,则最小公倍数是这两个数的乘积;两个数为倍数关系,则最小公倍数为较大的数;两个数有公约数的,最小公倍数是两个数公有质因数与独有质因数的连乘积;由此选择情况解决问题。
【详解】
如果两个数的最大因数是1,说明这两个数互质,那么这两数的最小公倍数就是它们的乘积。此说法正确。
故答案为√。
【点睛】
此题主要考查两个是互质关系时求最小公倍数的方法,这两个数的最小公倍数是它们的乘积。
29.×
【解析】
【分析】
分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数;本题中,没有说明是“平均分”,所以每段就不一定是这根铁丝的;据此判断。
【详解】
把一根铁丝分成6段,没有说明是平均分成6段,所以每段就不一定是这根铁丝的。
故判断为:×。
【点睛】
解答本题要明确单位“1”和分数的意义,要明确“平均分”这一前提条件。
30.错误
【解析】
【详解】
试题分析:既是6的倍数又是8的倍数的数有无数个,如:24、48、72等,据此判断即可.
解:6和8的最小公倍数是24,既是6的倍数又是8的倍数的数有无数个,如:24、48、72等,
故答案为错误.
点评:此题主要考查两个数的公倍数的个数.
31.×
【解析】
【分析】
根据分数的意义可知,分母表示平均分的总份数,分子表示取其中的份数,依此判断。
【详解】
把一个蛋糕平均分成8份,每份是这个蛋糕的。
故答案为:×
【点睛】
熟练掌握分数的意义是解答此题的关键。
32.×
【解析】
略
33.;;
【解析】
【详解】
试题分析:在分数中,分子与分母只有公因数1的分数为最简分数.据此将题目中的分数进行约分即能将它们化成最简分数.
解:==;
==;
==.
点评:在约分时,要注意确定分子与分母的最大公约数是多少.
34.小强
【解析】
【详解】
7÷13=
5÷8= = =
因为<,所以小强的画画速度快.
35.第三天 第一天
【解析】
【详解】
因为<<,所以第三天运走的最多,第一天运走的最少.
36.80 (1+2+3)= 13 (组)……2(个)
红球:13×1+1=14(个) 14÷ 80 =
白球:13×2+1=27(个) 27÷80 =
黄球:13×3 =39(个) 39÷80 =
【解析】
【详解】
略
37.8件
【解析】
【分析】
根据题意可知,每5名同学可以做1件手工作品,因此直接计算出40名同学里面含5名同学的个数,40名同学里面含5名同学的个数也就等于40名同学可以做手工作品的件数,依此解答。
【详解】
40÷(15÷3)
=40÷5
=8(件)
答:一共可以做8件手工作品。
【点睛】
熟练掌握工程问题的计算是解答此题的关键。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.小时是( )分钟。
A.15 B.12 C.20 D.25
2.把吨煤平均分成4份,每份是1吨的( )
A. B. C. D.
3.甲队6天修路48千米,乙队4天修路24千米。甲队6天修的路乙队需要多少天?下面列式正确的是( )。
A.24÷4×6 B.48÷6×4 C.48÷(24÷4)
4.一个最简分数,如果分母中只含有因数(),再无其他因数,那么这个分数可以化成有限小数;否则就不能化成有限小数.
A.2 和3 B.3 C.3和 5 D.2和5
5.下列分数中,能化成有限小数的是( )
A. B. C.
6.下面各数中,不能化成有限小数的是( )。
A. B. C. D.
7.两根同样长的绳子,第一根剪去,第二根剪去米,第一根余下的比第二根余下的长.那么每根绳长( )
A.比1米长 B.比1米短 C.等于1米
二、其他计算
8.分数和小数互化。
0.15= (保留两位小数)≈
9.把下面的分数约分,是假分数的要化成带分数或整数。
= = =
10.将下面的假分数化成带分数或整数。
= = = =
11.把下面的假分数化成带分数。
= = =
12.求下列各组数的最大公因数和最小公倍数。
15和16 29和87 24和64
三、填空题
13.有一个最简分数,把分子加上分母,分母也加上分母,所得到的新分数是原分数的9倍,这个最简分数是 .
14.用分数表示下面各图中的涂色部分,并读一读.
15.写出3个与相等的分数,是( )、( )、( )。
16.如果a÷=b÷30=c÷(a、b、c均不为0),这三个数从小到大的排列是 < < .
17.甲数的等于乙数的,甲数比乙数大(甲、乙均不为0). .(判断对错)
18.在括号里填上“>”“<”或“=”。
( ) 2.4÷1.5( )2.4
19.甲数÷乙数=6,甲、乙两数的最小公倍数是________.
20.
上面小棒的是 根;圈出它的.
21.一个最简分数的分子加上10,分母加上14后大小却不变,这个最简分数是 .
22.一根绳子长20米,平均剪成5段,每段是全长的 ,如果剪下它的是 米.
23.> >> >.
24.在横线里填上>、<或=.
5﹣3× 2×
÷+÷ (+)÷.
25.一份稿件,甲单独用计算机录入要用8小时,乙单独用计算机录入要用10小时.
(1)甲先录入3小时,剩下的由乙录入,还要用_____小时.
(2)甲先录入3小时,余下的两人合作,还要_____小时.
(3)甲、乙合作录入3小时,剩下的由甲单独录入.还要_____小时.
(带分数,先填写整数部分,再填写分子部分,最后填写分母部分)
26.把一条3分米长的纸条对折再对折,对折后每段的长度是全长的 ,每段长________分米.
四、判断题
27.和相等的分数有无数个. ___
28.如果两个数的最大因数是1,那么这两数的最小公倍数就是它们的乘积。( )
29.一根铁丝分成6段,每段是这根铁丝的。( )
30.既是6的倍数又是8的倍数的数只有48. .
31.把一个蛋糕分成8份,每份是这个蛋糕的。( )
32.梨树棵数的相当于苹果树棵数,是把苹果树棵数看作单位“1”.( )
五、解答题
33.将下列各分数化成最简分数.
,,.
34.小明13分钟画了7辆小汽车,小强8分钟画了5辆小汽车,谁的画画速度比较快?
35.一批货物,第一天运走它的,第二天运走它的,第三天运走它的.哪天运走的最多?哪天运走的最少?
36.有一串彩球,按1个红球、2个白球就、3个黄球的规律排列,这串彩球共80个.三种颜色的求各占总数的几分之几?
37.三(6)班手工兴趣小组的15名学生做了3件手工作品。照这样计算,兴趣小组有40名学生,一共可以做几件手工作品?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
1小时是60分钟,小时也就是60分钟的,把60分钟平均分成4份,取走1份即可。
【详解】
1小时是60分钟,60分钟的是15分钟;
故答案选:A。
【点睛】
化成小数是0.25,大单位化小单位乘进率,0.25乘60,得到15分钟。
2.A
【解析】
【详解】
试题分析:根据分数的意义,把吨煤平均分成4份,每份就是这“吨煤”的,所以每份重×=吨.同理,吨也就是1吨煤的.
解:×=(吨)
所以把吨煤平均分成4份,每份是1吨的;
故选A.
【点评】本题重点考查了分数的意义.
3.C
【解析】
【分析】
首先根据:工作效率=工作量÷工作时间,用乙队修路的长度除以用的时间,求出乙队每天修路多少千米;然后用甲队6天修路的长度除以乙队每天修路的长度,求出甲队6天修的路乙队需要多少天即可。
【详解】
48÷(24÷4)
=48÷6
=8(天)
故答案为:C
【点睛】
此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率。
4.D
【解析】
【详解】
分母中只有2、5因子的分数,它们总可以把2和5一个配一个相乘而成一个个的10连乘(缺多少2或5就可以根据分数的性质给分子分母同乘而补足),结果分母总能成了100......00型,这样的分数当然就能化成有限小数了.
故选D
此题主要考察分数和小数的互化
5.C
【解析】
【详解】
试题分析:首先,要把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
解:的分母中含有质因数3,所以不能化成有限小数;
的分母中含有质因数3,所以不能化成有限小数;
化简后是,分母中只有质因数5,所以能化成有限小数.
故选C.
【点评】此题主要考查什么样的分数可以化成有限小数,根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.就能很快判断出什么样的分数能化成有限小数,什么样的分数不能化成有限小数.
6.A
【解析】
【分析】
分数化为小数,直接用分子除以分母,据此将每个选项中的分数都互为小数,再进行判断选择即可。
【详解】
A.≈0.83;
B.=0.25;
C.=0.3125;
D.=0.375;
故答案为:A。
【点睛】
熟练掌握分数与小数的互化方法是解答本题的关键。
7.B
【解析】
【详解】
试题分析:一个数乘上大于1的数,积大于这个数;一个数乘上1,积等于这个数;一个数乘上小于1的数,积小于这个数,据此解答.
解:因两根同样长的绳子,第一根剪去,第二根剪去米,
(1)当绳子长度大于1米时,乘上的绳子长度大于米,用去的比第二根多,剩下的绳子就比第二根剩下的短;
(2)当绳子长度等于1米时,乘上绳子的长度等于米,用去的和第二根一样长,剩下的绳子就和第二根剩下的一样长;
(3)当绳子长度小于1米时,乘上绳子的长度小于米,用去的比第二根少,剩下的绳子就比第二根剩下的长.
故选B.
点评:本题考查了学生对于一个数同另一个数相乘,积与这个数大小知识情况的掌握.
8.0.36;;0.53
【解析】
【分析】
分数化成小数,分子除以分母,商用小数表示;小数化成分数,原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分,据此解答。
【详解】
9÷25=0.36;0.15= = ;≈0.53
【点睛】
此题考查了分数、小数的互化,掌握方法,认真计算即可。
9.;1;5
【解析】
【分析】
首先根据约分的方法,把下面各分数进行约分,再根据假分数化成带分数的方法:把假分数化成带分数,用分子除以分母得到的商作整数部分,余数作分子,分母不变,能整除的可以化成整数;据此解答。
【详解】
==
===1
===5
10.1;;;
【解析】
【分析】
假分数化成带分数或整数需要注意:假分数化成整数或者带分数时,假分数的分子除以分母,能整除的,所得的商就是整数;当不能整除时,所得的商就是带分数的整数部分,余数是分数部分的分子,分母不变。
【详解】
5÷5=1;所以=1;
9÷8=1……1;所以=;
15÷13=1……2;所以=;
9÷2=4……1;所以=
【点睛】
根据假分数化成带分数或整数的方法细心解答即可。
11.4;2;1
【解析】
【分析】
假分数化整数或带分数的方法是用分子除以分母,商为整数部分,余数作分子,分母不变。
【详解】
=4;
=2=2;
=1。
12.15和16的最大公因数是1,最小公倍数是240
29和87的最大公因数是29,最小公倍数是87
24和64的最大公因数是8,最小公倍数是192
【解析】
【分析】
对于两个数来说:两个数的公有质因数连乘积是最大公因数,两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数,由此解决问题即可。
【详解】
(1)15和16互质,
15和16的最大公因数是1,最小公倍数是15×16=240。
(2)29和87成倍数关系,
所以29和87的最大公因数是29,最小公倍数是87。
(3)24和64
24=2×2×2×3,64=2×2×2×2×2×2,
24和64的最大公因数是2×2×2=8,最小公倍数是2×2×2×2×2×2×3=192。
【点睛】
如果两个数互质,它们的最大公因数是1,这两个数的积就是它们的最小公倍数;如果两个数成倍数关系,较小的数就是这两个数的最大公因数,较大的数就是这两个数的最小公倍数。如果数据较大则用短除法的形式求。
13.
【解析】
【详解】
试题分析:根据题意,设原分数的分子为,则有:,由此解答.
解:设原分数的分子为,
则有:,
,
,
b+a=18b,
a=17b;
所以.
答:这个最简分数是.
故答案为.
点评:此题主要考查最简分数的意义,根据题意列方程解答比较简便.
14.
【解析】
【详解】
试题分析:分数的意义为:把单位“1”平均分成若干份,表示其中这样一份或几份的数叫分数.据此解答即可.
解:
因为图4,不是平均分成三份,所以阴影不可以用分数表示.
点评:明确分数的意义,是解答此题的关键.
15.
【解析】
【分析】
根据分数的基本性质,分数的分子和分母同时扩大或缩小,分数的大小不变。
【详解】
(1)==
(2)==
(3)==
答案不唯一。
【点睛】
本题考查分数的基本性质,只要分子和分母同时乘以2、3、4就能得到3个分数。
16.b、a、c
【解析】
【详解】
试题分析:先利用除以一个数,就等于乘这个数的倒数,将原式进行变形,再化成同分母分数比较出三个分数的大小,最后依据“积一定的情况下,一个因数大,另一个因数就小”的规律,即可求出三个数的大小.
解:因为a÷=b÷30=c÷,
即a×=b×=c×20,
又因=,20=,
且<<,
所以b<a<c;
故答案为b、a、c.
点评:此题主要考查同分母分数大小比较的方法,以及积一定的情况下,因数的变化规律.
17.正确
【解析】
【详解】
试题分析:由题意知:甲数×=乙数×,根据比例的性质求出甲乙两数的比,即可比较出两数的大小.
解:由题意知:甲数×=乙数×,
甲数:乙数=:=×4=4:3,
可知甲数比乙数大.
故答案为正确.
点评:本题主要考查学生灵活运用比例的性质求出比,进而进行两数的大小比较.
18. > <
【解析】
【分析】
①可先找到两个分数的最小公分母,把两个分数通分,再比较大小即可;
②可根据商与被除数的关系,结合具体数值,进行大小比较。
【详解】
①==
==
因为>
所以>
②1.5>1,根据一个非零数除以一个大于1的数,商小于它本身可得:2.4÷1.5<2.4。
【点睛】
本题应用了通分,以及商与被除数的关系来解答,通分时找最小公分母会使运算较为简便。
19.甲数
【解析】
【详解】
略
20.10
【解析】
【详解】
试题分析:由图可知,图中共有12根据小棒,根据分数的意义,这些小棒的即将这些小棒平均分成6份,取其中的5份,12×=10根,其是将这些小棒平均分成3份,取其中的1份,即12×=4根.
解:12×=10(根);
即面小棒的是10根.
12×=4(根),如图:
故答案为10.
点评:本题的知识点:(1)求一个数的几分之几是多少,用乘法;(2)分数的意义.
21.
【解析】
【详解】
试题分析:分子增加10,那么10是原来分子的倍数;分母增加14,14是原来分母的倍数;而且这两个倍数相同,把10和14分解质因数,找出10和14的最大公约数就是这个倍数,10和14除以这个倍数就是原来分子和分母,进而写出这个分数.
解:10=2×5,
14=2×7;
10和14的最大公约数是2,10是原来分子的2倍,14是原来分母的2倍;
10÷2=5,
14÷2=7;
原来的分数是.
故答案为.
点评:本题也可以设原来的分数是,分子和分母增加后的分数是,根据分数大小不变列出方程,求出x和y的最简整数比即可求解.
22.,8
【解析】
【详解】
试题分析:一根绳子长20米,平均剪成5段,根据分数的意义,即将这根绳子全长当做单位“1”平均分成5份,则每份是全长的1÷5=;它的是20×=8(米).
解:每份是全长的:1÷5=;
它的是:20×=8(米).
故答案为,8.
点评:完成本题的依据为分数的意义:将单位“1”平均分成若干份,表示这样一份或几份的数为分数.
23.,
【解析】
【详解】
试题分析:把、,分别化成同分母的分数,再进行填空即可.
解:因为:,,
所以大于小于,
即,>.
因为:,,
所以>.
故答案为,.
点评:本题运用通分的方法进行解答即可.
24.>,=
【解析】
【详解】
试题分析:(1)可根据分数乘法与除法的运算法则有四则混合运算的运算顺序分别计算出两边算式的结果后进行比较.
(2)可根据乘法分配律进行分析比较.
解:(1)5﹣3×
=5﹣,
=;
2×=;
,
则5﹣3×>2×.
(2)÷+
=×+×
=(+).
(+)÷
=(+)×.
则÷+÷=(+)÷.
故答案为>,=.
点评:完成本题要认真分析计算两边的算式中的数据,然后做出正确的判断.
25. 6 2 2
【解析】
【分析】
不知道工作总量具体是多少,将工作总量看作是单位“1”.可求出甲的工作效率是,乙的工作效率是,两个人合作的工作效率为.
(1)甲录入3小时,剩下的工作总量为1﹣×3=,求乙的工作时间,用剩下的工作总量除以乙的工作效率即可.
(2)甲录入3小时,剩下的工作总量为1﹣×3=,求合作的工作时间,用剩下的工作总量除以合作的工作效率即可.
(3)甲、乙合作录入3小时,剩下的工作总量为1﹣×3=,求甲的工作时间,用剩下的工作总量除以甲的工作效率即可.
【详解】
(1)1÷8=
1÷10=
1﹣×3=
÷=6(小时)
(2)=
1﹣×3=
÷=2(小时)
(3)1﹣×3=
÷=2(小时)
故答案为:6;2;2.
【点睛】
本题考查工程问题需要注意:
①工程问题三个基本量之间的关系,即工作总量=工作效率×工作时间.
②当不知道工作总量具体是多少时,把工作总量看作是单位“1”.
③合作的工作效率等于工作效率的和.
26.
【解析】
【详解】
略
27.√
【解析】
【分析】
本题运用分数的大小比较进行解答,只要分母是分子的2倍的分数都与相等,因此这样的分数有无数个,所以本题的说法是正确的.
【详解】
分母是分子2倍的分数有:、、、…这样的分数有无数个且最简分数值是,
所以本题说法是正确的.
28.√
【解析】
【分析】
求两个数的最小公倍数,要看两个数之间的关系:两个数互质,则最小公倍数是这两个数的乘积;两个数为倍数关系,则最小公倍数为较大的数;两个数有公约数的,最小公倍数是两个数公有质因数与独有质因数的连乘积;由此选择情况解决问题。
【详解】
如果两个数的最大因数是1,说明这两个数互质,那么这两数的最小公倍数就是它们的乘积。此说法正确。
故答案为√。
【点睛】
此题主要考查两个是互质关系时求最小公倍数的方法,这两个数的最小公倍数是它们的乘积。
29.×
【解析】
【分析】
分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数;本题中,没有说明是“平均分”,所以每段就不一定是这根铁丝的;据此判断。
【详解】
把一根铁丝分成6段,没有说明是平均分成6段,所以每段就不一定是这根铁丝的。
故判断为:×。
【点睛】
解答本题要明确单位“1”和分数的意义,要明确“平均分”这一前提条件。
30.错误
【解析】
【详解】
试题分析:既是6的倍数又是8的倍数的数有无数个,如:24、48、72等,据此判断即可.
解:6和8的最小公倍数是24,既是6的倍数又是8的倍数的数有无数个,如:24、48、72等,
故答案为错误.
点评:此题主要考查两个数的公倍数的个数.
31.×
【解析】
【分析】
根据分数的意义可知,分母表示平均分的总份数,分子表示取其中的份数,依此判断。
【详解】
把一个蛋糕平均分成8份,每份是这个蛋糕的。
故答案为:×
【点睛】
熟练掌握分数的意义是解答此题的关键。
32.×
【解析】
略
33.;;
【解析】
【详解】
试题分析:在分数中,分子与分母只有公因数1的分数为最简分数.据此将题目中的分数进行约分即能将它们化成最简分数.
解:==;
==;
==.
点评:在约分时,要注意确定分子与分母的最大公约数是多少.
34.小强
【解析】
【详解】
7÷13=
5÷8= = =
因为<,所以小强的画画速度快.
35.第三天 第一天
【解析】
【详解】
因为<<,所以第三天运走的最多,第一天运走的最少.
36.80 (1+2+3)= 13 (组)……2(个)
红球:13×1+1=14(个) 14÷ 80 =
白球:13×2+1=27(个) 27÷80 =
黄球:13×3 =39(个) 39÷80 =
【解析】
【详解】
略
37.8件
【解析】
【分析】
根据题意可知,每5名同学可以做1件手工作品,因此直接计算出40名同学里面含5名同学的个数,40名同学里面含5名同学的个数也就等于40名同学可以做手工作品的件数,依此解答。
【详解】
40÷(15÷3)
=40÷5
=8(件)
答:一共可以做8件手工作品。
【点睛】
熟练掌握工程问题的计算是解答此题的关键。
答案第1页,共2页
答案第1页,共2页
