2021-2022学年度高一下数学一课一练9.2用样本估计总体(Word含解析)
文档属性
| 名称 | 2021-2022学年度高一下数学一课一练9.2用样本估计总体(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 481.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 08:57:02 | ||
图片预览




文档简介
9.2用样本估计总体
一、单选题
1.茶叶源于中国,至今中国仍然是茶叶最大生产国,下图为年全球主要茶叶生产国调查数据.
年全球主要茶叶生产国产量分布
根据该图,下列结论中不正确的是( )
A.年图中个国家茶叶产量的中位数为
B.年图中个国家茶叶产量比年增幅最大的是中国
C.年图中个国家茶叶总产量超过年
D.年中国茶叶产量超过其他个国家之和
2.已知某样本的容量为100,平均数为80,方差为95.现发现在收集这些数据时,其中的两个数据记录有误,一个错将90记录为70,另一个错将80记录为100.在对错误的数据进行更正后,重新求得样本的平均数为,方差为,则( )
A., B., C., D.,
3.已知某班男女同学人数之比为,该班所有同学进行毽球(踢毽子)比赛,比赛规则如下:每个同学用脚踢起毽球,在毽球落地前用脚接住并踢起,脚没有接到毽球则比赛结束.现记录了每个同学用脚踢起毽球开始到毽球落地,脚踢到毽球的次数,已知男同学用脚踢到毽球次数的平均数为21,方差为17,女同学用脚踢到毽球次数的平均数为12,方差为17,那么全班同学用脚踢到毽球次数的平均数和方差分别为( )
A.16,38 B.16,37 C.17,38 D.17,37
4.年以前,北京市先后组织实施了多个阶段的大气污染防治行动,针对燃煤 工业 扬尘排放和机动车排放等采取了数百项治理措施.2008年北京市首次探索区域联防联控,取得了良好效果.2013年北京市制定实施以防治细颗粒物为重点的《2013-2017年清洁空气行动计划》,治理成效显著.
上图是2000年至2018年可吸入颗粒物 细颗粒物 二氧化氮 二氧化硫等主要污染物年日均值的折线图.根据图中信息,下列结论中正确的是( )
A.2013年到2018年,空气中可吸入颗粒物的年日均值逐年下降
B.2013年到2018年,空气中细颗粒物的年日均值逐年下降
C.2000年到2018年,空气中二氧化氮的年日均值都低于40微克/立方米
D.2000年到2018年,空气中二氧化硫的年日均值最低的年份是2008年
5.已知在一次射击预选赛中,甲,乙两人各射击10次,两人成绩的条形统计图如图所示,则下列四个选项中判断正确的是( )
A.甲的成绩的平均数大于乙的成绩的平均数
B.甲的成绩的中位数大于乙的成绩的中位数
C.甲的成绩的方差大于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
6.某同学掷骰子5次,并记录每次骰子出现的点数.则可以判断出这组数据一定没有出现点数6的是( )
A.平均数为3,中位数为2 B.中位数为3,众数为2
C.中位数3,方差为2.8 D.平均数为2,方差为2.4
二、多选题
7.为唤起学生爱护地球 保护家园的意识,加强对节能减排的宣传,进一步营造绿色和谐的校园环境,树人中学决定举办环保知识竞赛.现有甲 乙 丙 丁四个班级参加,每个班级各派10位同学参赛,每位同学需要回答10道题,每题回答正确得1分,回答错误得0分.若规定总得分达到70分且没有同学得分低于5分的班级为“优胜班级”,则根据以下甲 乙 丙 丁各班参赛同学的得分数据信息,能判断该班一定为“优胜班级”的是( )
A.甲班同学平均数为8,众数为8 B.乙班同学平均数为8,方差为4
C.丙班同学平均数为7,极差为3 D.丁班同学平均数为7,标准差为0
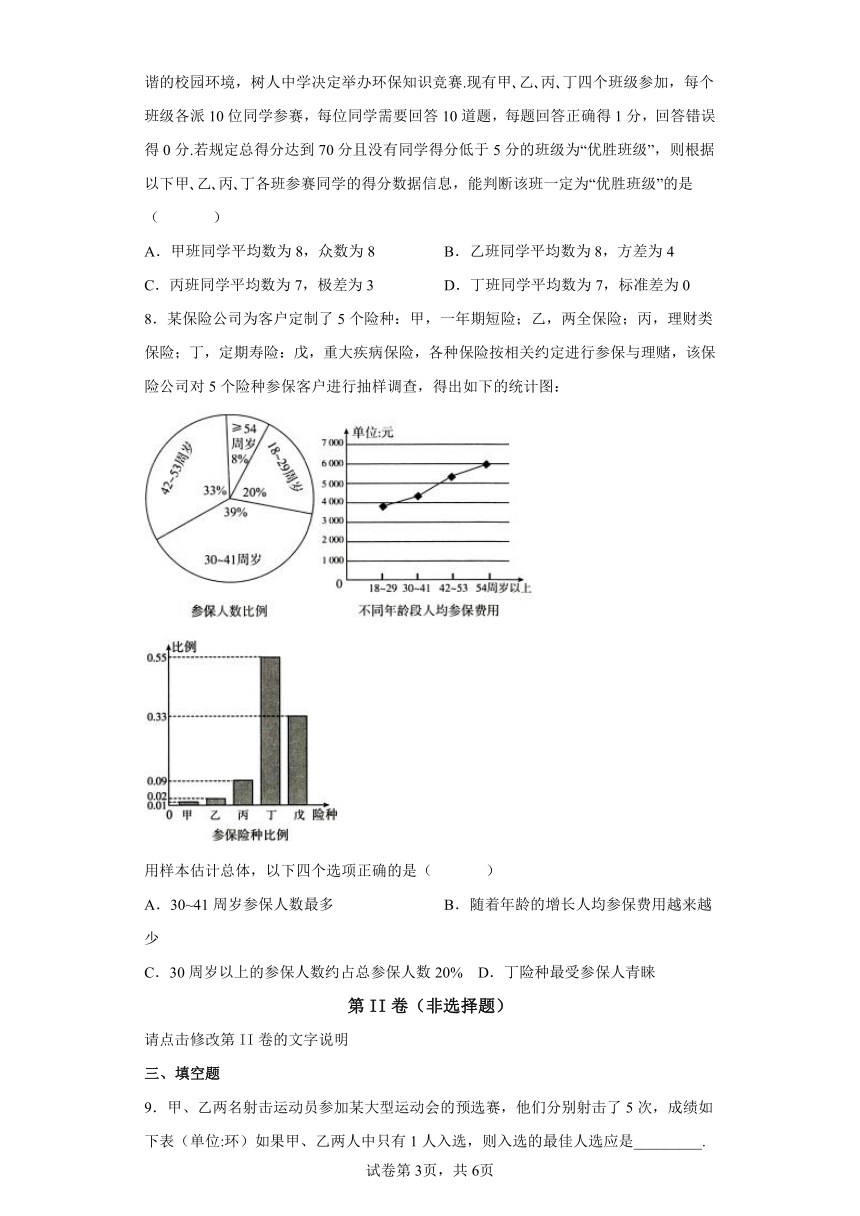
8.某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赌,该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图:
用样本估计总体,以下四个选项正确的是( )
A.30~41周岁参保人数最多 B.随着年龄的增长人均参保费用越来越少
C.30周岁以上的参保人数约占总参保人数20% D.丁险种最受参保人青睐
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别射击了5次,成绩如下表(单位:环)如果甲、乙两人中只有1人入选,则入选的最佳人选应是_________.
10.数据,,…,的平均数是3,方差是1,则数据,,…,的平均数和方差之和是__________.
11.若一组数据的平均数为10,方差为2,则__________.
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是______________
①平均数;
②平均数且标准差;
③平均数且极差小于或等于2;
④众数等于1且极差小于或等于4.
四、解答题
13.为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:)的数据如下:
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图;
(2)估计甲、乙两运动员的最大速度的均值和方差,并判断谁参加比赛更合适.
14.某工厂有工人名,其中名工人参加过短期培训(称为类工人),另外名工人参加过长期培训(称为类工人).现用分层抽样方法(按类,类分二层)从该厂的工人中共抽取名工人,调查他们的生产能力(生产能力指一天加工的零件数)
(1)类工人和类工人各抽取多少人
(2)将类工人的抽查结果分别绘制成频率分布直方图(如图1),根据频率分布直方图通过计算估计类工人的中位数,众数,平均数(同一组中的数据用该组区间的中点值作代表)
(3)就生产能力而言,类工人中个体间的差异程度与类工人个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
15.从某学校随机抽取100名学生,测得他们的身高(单位:cm),按照区间,,,,分组,得到样本身高的频率分布直方图,如图所示.
(1)求频率分布直方图中x的值;
(2)估计该校学生身高的平均数(每组数据以区间中点值为代表);
(3)估计该校学生身高的75%分位数.
16.甲、乙、丙三台机床同时生产一种零件,在天中,甲乙机床每天生产的次品数如下表所示:
第天 第天 第天 第天 第天 第天 第天 第天 第天 第天
甲
乙
(1)分别计算这两组数据的平均数和方差;
(2)已知丙机床这天生产次品数的平均数为,方差为.以平均数和方差为依据,若要从这三台机床中淘汰一台,你应该怎么选择?这三台机床你认为哪台性能最好?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
根据统计图表提供的数据判断各选项.
【详解】
图中,2019年的数据中间的一个是45.9,A正确;
2020年图中个国家茶叶产量比年增幅最大的是肯尼亚,B错;
2020年图中个国家茶叶总产量比年总产量的差是,
C正确;
年图中,D正确,
故选:B.
2.A
【解析】
【分析】
根据题中所给的平均数的条件,重新列式求新数据的平均数,根据方差公式写出两组数据的方差,并比较大小.
【详解】
由题意,可得,
设收集的98个准确数据分别记为,
则
,
,所以.
故选:A
3.D
【解析】
【分析】
设男生有5人,且用脚踢到毽球次数分别为,,,,,设女生有4人,用脚踢到毽球次数分别为,,,,根据平均数和方差的计算方法计算即可.
【详解】
设该班有男生5人,且用脚踢到毽球次数分别记为,,,,,设女生4人,且用脚踢到毽球次数分别记为,,,.
则男生踢到毽球次数的平均数,方差,
即,女生踢到毽球次数的平均数,
方差,即.
故全班同学踢到毽球次数的平均数为,
方差为
.
故选:D.
4.B
【解析】
观察折线图,确定数据的变化规律,判断各选项.
【详解】
2014年空气中可吸入颗粒物年日均值比2013年多,A错;
2013年到2018年,空气中细颗粒物的年日均值逐年下降,B正确;
2007年(含2007年)之前空气中二氧化氮的年日均值都高于40微克/立方米,C错;
2000年到2018年,空气中二氧化硫的年日均值最低的年份是2018年,D错.
故选:B.
5.C
【解析】
【分析】
根据条形统计图可分别计算出甲、乙的平均数、中位数、极差,从而判断出ABD的正误;根据成绩的分散程度可判断C的正误.
【详解】
对于A,甲的成绩的平均数为:,乙的成绩的平均数为:,甲的成绩的平均数小于乙的成绩的平均数,故错误;
对于B,甲的成绩的中位数为:;乙的成绩的中位数为:,甲的成绩的中位数小于乙的成绩的中位数,故B错误;
对于C,由条形统计图得甲的成绩相对分散,乙的成绩相对稳定,甲的成绩的方差大于乙的成绩的方差,故C正确;
对于D,甲的成绩的极差为:;乙的成绩的极差为:,甲的成绩的极差大于乙的成绩的极差,故D错误.
故选:C
6.D
【解析】
【分析】
根据题意错误命题举出反例即可解出.
【详解】
对于,当投掷骰子出现结果为, 6时,满足平均数为3,中位数为2,可以出现点数6,故A错误;
对于B,当投掷骰子出现结果为2, 2, 3,4, 6时,满足中位数为3,众数为2,可以出现点数6,故B错误;
对于C,当投郑骰子出现结果为,6时,满足中位数为3, 平均数为: ,方差为
,可以出现点数 6,故C错误;
对于D,若平均数为2,且出现6点,则方差,
平均数为2,方差为2.4时,一定没有出现点数6,故D正确;
故选:D.
7.CD
【解析】
【分析】
对于A,可举例有得分低于5分的情况,判断其是否能判断该班一定为“优胜班级”,同理可判断B,对于C项,用反证法的思想来说明其可能,对于D,直接判断得分情况,可以说明其可能性.
【详解】
对于A,比如有一位同学得2分,三位同学得10分,其余六位同学都得8分,满足平均数为8,众数为8,但不满足总得分达到70分且没有同学得分低于5分,故A不能保证该班一定为“优胜班级”;
对于B,10位同学的得分可能是:4,6,6,8,8,8,10,10,10,10,此时满足平均数为8,方差为4
但不满足总得分达到70分且没有同学得分低于5分,故B不能保证该班一定为“优胜班级”;
对于C,如果有同学得分低于5分,根据极差为3,那么就,会出现其他同学的得分不大于7,这样平均分就低于7分,不符合丙班同学平均数为7,极差为3的条件,故这种情况下不会有得分低于5分的同学,满足总得分达到70分且没有同学得分低于5分,故C能保证该班一定为“优胜班级”;
对于D, 丁班同学平均数为7,标准差为0,可知每位同学得分均为7分,故D能保证该班一定为“优胜班级”,
故选:CD.
8.AD
【解析】
【分析】
根据选项逐一对相应的统计图进行分析判断即可.
【详解】
对A:由扇形图可知,31~41周岁的参保人数最多,故选项A正确;
对B:由折线图可知,随着年龄的增长人均参保费用越来越多,故选项B错误;
对C:由扇形图可知,30周岁以上的参保人数约占总参保人数的80%,故选项C错误;
对D:由柱状图可知,丁险种参保比例最高,故选项D正确.
故选:AD.
9.甲
【解析】
【详解】
,
又,
,
,所以入选的最佳人选应是甲.
10.3
【解析】
【详解】
分析:由题意结合平均数、方差的性质整理计算即可求得最终结果.
详解:由题意结合平均数和方差的性质可知:
数据,,…,的平均数为:,方差为:,
则平均数和方差之和是.
点睛:本题主要考查均值的性质、方差的性质等知识,意在考查学生的转化能力和计算求解能力.
11.
【解析】
【分析】
根据题意得,,进而解方程即可得答案.
【详解】
解:根据题意得平均数,
方差
即,,解得或,
所以
故答案为:
12.②③④
【解析】
【分析】
根据各个选项,分别分析新增人数的最大值是否可能大于5,即可得结论.
【详解】
仅仅平均值不大于3,有可能其中某个值大于5,①不符合;
平均数时,若7天中有一个数值大于5,则方差,因此在标准差时,7天的数据都不超过5,②符合指标;
平均数且极差小于或等于2,最大值必不大于5,③符合指标;
众数等于1且极差小于或等于4时,最大值必不大于5,否则极差大于6-1=5,④符合指标.
故答案为:②③④
【点睛】
本题考查平均数,标准差,极差,众数等概念,掌握这些概念,能用反证法是解题关键.
13.(1)茎叶图见解析;(2)派乙更合适
【解析】
【分析】
(1)根据茎叶图的画法可画出茎叶图;
(2)利用平均数公式分别求得甲、乙的平均数,利用方差公式分别求得甲、乙的方差,比较平均数与方差的大小,根据平均数与方差的实际意义可得结论.
【详解】
(1)茎叶图如下:
(2)甲的平均数为:=33,
乙的平均数为:(28+29+33+34+36+38)=33,
甲的方差为:,
乙的方差为:,
甲、乙的平均数相等,乙的方差更小,则乙的发挥更稳定,故乙参加比赛更合适.
14.(1);
(2);;
(3)类工人个体间的差异程度更小
【解析】
【分析】
(1)根据分层抽样的概念直接计算;
(2)根据频率分布直方图,利用中位数,众数,平均数的概念及公式直接计算;
(3)根据频率分布直方图直接可得结论.
(1)
解:由已知分层抽样可得:类工人抽取人,类工人抽取人;
(2)
解:中位数:设中位数为,由频率分布直方图可得,,所以,且,解得:,即中位数为;
众数:由频率分布直方图可得众数为;
平均数:,即平均数为;
(3)
根据频率分布直方图可判断类工人个体间的差异程度更小.
15.(1)0.06
(2)172.25
(3)176.25
【解析】
【分析】
(1)利用频率分布直方图中长方形面积之和为1,易求出x;
(2)直接利用平均数公式求出平均数;
(3)可设该校100名生学身高的75%分位数为x,再利用频率分布直方图计算即得
(1)
由频率分布直方图可知5×(0.01+0.07+x+0.04+0.02+0.01)=1,解得x=0.06,
(2)
根据频率分布直方图,由平均数公式可得:
(3)
的人数占比为5×0.02=10%.
的人数占比为5×00.4=20%.
所以该校100名生学身高的75%分位数落在.
设该校100名生学身高的75%分位数为x,则,解得x=176.25.
故该校100名生学身高的75%分位数为176.25.
16.(1),,,;(2)淘汰丙机床,乙机床的性能最好.
【解析】
【分析】
(1)根据平均数,方差的定义求两组数据的平均数和方差;
(2)根据平均数的意义和方差的意义判断三台机床哪台性能最好,哪台性能最差.
【详解】
(1),
,
,
.
(2)因为,,
所以次品数的平均数最小的是乙,稳定性最好的也是乙,稳定性最差的是丙,
故应淘汰丙机床,乙机床的性能最好.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.茶叶源于中国,至今中国仍然是茶叶最大生产国,下图为年全球主要茶叶生产国调查数据.
年全球主要茶叶生产国产量分布
根据该图,下列结论中不正确的是( )
A.年图中个国家茶叶产量的中位数为
B.年图中个国家茶叶产量比年增幅最大的是中国
C.年图中个国家茶叶总产量超过年
D.年中国茶叶产量超过其他个国家之和
2.已知某样本的容量为100,平均数为80,方差为95.现发现在收集这些数据时,其中的两个数据记录有误,一个错将90记录为70,另一个错将80记录为100.在对错误的数据进行更正后,重新求得样本的平均数为,方差为,则( )
A., B., C., D.,
3.已知某班男女同学人数之比为,该班所有同学进行毽球(踢毽子)比赛,比赛规则如下:每个同学用脚踢起毽球,在毽球落地前用脚接住并踢起,脚没有接到毽球则比赛结束.现记录了每个同学用脚踢起毽球开始到毽球落地,脚踢到毽球的次数,已知男同学用脚踢到毽球次数的平均数为21,方差为17,女同学用脚踢到毽球次数的平均数为12,方差为17,那么全班同学用脚踢到毽球次数的平均数和方差分别为( )
A.16,38 B.16,37 C.17,38 D.17,37
4.年以前,北京市先后组织实施了多个阶段的大气污染防治行动,针对燃煤 工业 扬尘排放和机动车排放等采取了数百项治理措施.2008年北京市首次探索区域联防联控,取得了良好效果.2013年北京市制定实施以防治细颗粒物为重点的《2013-2017年清洁空气行动计划》,治理成效显著.
上图是2000年至2018年可吸入颗粒物 细颗粒物 二氧化氮 二氧化硫等主要污染物年日均值的折线图.根据图中信息,下列结论中正确的是( )
A.2013年到2018年,空气中可吸入颗粒物的年日均值逐年下降
B.2013年到2018年,空气中细颗粒物的年日均值逐年下降
C.2000年到2018年,空气中二氧化氮的年日均值都低于40微克/立方米
D.2000年到2018年,空气中二氧化硫的年日均值最低的年份是2008年
5.已知在一次射击预选赛中,甲,乙两人各射击10次,两人成绩的条形统计图如图所示,则下列四个选项中判断正确的是( )
A.甲的成绩的平均数大于乙的成绩的平均数
B.甲的成绩的中位数大于乙的成绩的中位数
C.甲的成绩的方差大于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
6.某同学掷骰子5次,并记录每次骰子出现的点数.则可以判断出这组数据一定没有出现点数6的是( )
A.平均数为3,中位数为2 B.中位数为3,众数为2
C.中位数3,方差为2.8 D.平均数为2,方差为2.4
二、多选题
7.为唤起学生爱护地球 保护家园的意识,加强对节能减排的宣传,进一步营造绿色和谐的校园环境,树人中学决定举办环保知识竞赛.现有甲 乙 丙 丁四个班级参加,每个班级各派10位同学参赛,每位同学需要回答10道题,每题回答正确得1分,回答错误得0分.若规定总得分达到70分且没有同学得分低于5分的班级为“优胜班级”,则根据以下甲 乙 丙 丁各班参赛同学的得分数据信息,能判断该班一定为“优胜班级”的是( )
A.甲班同学平均数为8,众数为8 B.乙班同学平均数为8,方差为4
C.丙班同学平均数为7,极差为3 D.丁班同学平均数为7,标准差为0
8.某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赌,该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图:
用样本估计总体,以下四个选项正确的是( )
A.30~41周岁参保人数最多 B.随着年龄的增长人均参保费用越来越少
C.30周岁以上的参保人数约占总参保人数20% D.丁险种最受参保人青睐
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别射击了5次,成绩如下表(单位:环)如果甲、乙两人中只有1人入选,则入选的最佳人选应是_________.
10.数据,,…,的平均数是3,方差是1,则数据,,…,的平均数和方差之和是__________.
11.若一组数据的平均数为10,方差为2,则__________.
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是______________
①平均数;
②平均数且标准差;
③平均数且极差小于或等于2;
④众数等于1且极差小于或等于4.
四、解答题
13.为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:)的数据如下:
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图;
(2)估计甲、乙两运动员的最大速度的均值和方差,并判断谁参加比赛更合适.
14.某工厂有工人名,其中名工人参加过短期培训(称为类工人),另外名工人参加过长期培训(称为类工人).现用分层抽样方法(按类,类分二层)从该厂的工人中共抽取名工人,调查他们的生产能力(生产能力指一天加工的零件数)
(1)类工人和类工人各抽取多少人
(2)将类工人的抽查结果分别绘制成频率分布直方图(如图1),根据频率分布直方图通过计算估计类工人的中位数,众数,平均数(同一组中的数据用该组区间的中点值作代表)
(3)就生产能力而言,类工人中个体间的差异程度与类工人个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
15.从某学校随机抽取100名学生,测得他们的身高(单位:cm),按照区间,,,,分组,得到样本身高的频率分布直方图,如图所示.
(1)求频率分布直方图中x的值;
(2)估计该校学生身高的平均数(每组数据以区间中点值为代表);
(3)估计该校学生身高的75%分位数.
16.甲、乙、丙三台机床同时生产一种零件,在天中,甲乙机床每天生产的次品数如下表所示:
第天 第天 第天 第天 第天 第天 第天 第天 第天 第天
甲
乙
(1)分别计算这两组数据的平均数和方差;
(2)已知丙机床这天生产次品数的平均数为,方差为.以平均数和方差为依据,若要从这三台机床中淘汰一台,你应该怎么选择?这三台机床你认为哪台性能最好?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
根据统计图表提供的数据判断各选项.
【详解】
图中,2019年的数据中间的一个是45.9,A正确;
2020年图中个国家茶叶产量比年增幅最大的是肯尼亚,B错;
2020年图中个国家茶叶总产量比年总产量的差是,
C正确;
年图中,D正确,
故选:B.
2.A
【解析】
【分析】
根据题中所给的平均数的条件,重新列式求新数据的平均数,根据方差公式写出两组数据的方差,并比较大小.
【详解】
由题意,可得,
设收集的98个准确数据分别记为,
则
,
,所以.
故选:A
3.D
【解析】
【分析】
设男生有5人,且用脚踢到毽球次数分别为,,,,,设女生有4人,用脚踢到毽球次数分别为,,,,根据平均数和方差的计算方法计算即可.
【详解】
设该班有男生5人,且用脚踢到毽球次数分别记为,,,,,设女生4人,且用脚踢到毽球次数分别记为,,,.
则男生踢到毽球次数的平均数,方差,
即,女生踢到毽球次数的平均数,
方差,即.
故全班同学踢到毽球次数的平均数为,
方差为
.
故选:D.
4.B
【解析】
观察折线图,确定数据的变化规律,判断各选项.
【详解】
2014年空气中可吸入颗粒物年日均值比2013年多,A错;
2013年到2018年,空气中细颗粒物的年日均值逐年下降,B正确;
2007年(含2007年)之前空气中二氧化氮的年日均值都高于40微克/立方米,C错;
2000年到2018年,空气中二氧化硫的年日均值最低的年份是2018年,D错.
故选:B.
5.C
【解析】
【分析】
根据条形统计图可分别计算出甲、乙的平均数、中位数、极差,从而判断出ABD的正误;根据成绩的分散程度可判断C的正误.
【详解】
对于A,甲的成绩的平均数为:,乙的成绩的平均数为:,甲的成绩的平均数小于乙的成绩的平均数,故错误;
对于B,甲的成绩的中位数为:;乙的成绩的中位数为:,甲的成绩的中位数小于乙的成绩的中位数,故B错误;
对于C,由条形统计图得甲的成绩相对分散,乙的成绩相对稳定,甲的成绩的方差大于乙的成绩的方差,故C正确;
对于D,甲的成绩的极差为:;乙的成绩的极差为:,甲的成绩的极差大于乙的成绩的极差,故D错误.
故选:C
6.D
【解析】
【分析】
根据题意错误命题举出反例即可解出.
【详解】
对于,当投掷骰子出现结果为, 6时,满足平均数为3,中位数为2,可以出现点数6,故A错误;
对于B,当投掷骰子出现结果为2, 2, 3,4, 6时,满足中位数为3,众数为2,可以出现点数6,故B错误;
对于C,当投郑骰子出现结果为,6时,满足中位数为3, 平均数为: ,方差为
,可以出现点数 6,故C错误;
对于D,若平均数为2,且出现6点,则方差,
平均数为2,方差为2.4时,一定没有出现点数6,故D正确;
故选:D.
7.CD
【解析】
【分析】
对于A,可举例有得分低于5分的情况,判断其是否能判断该班一定为“优胜班级”,同理可判断B,对于C项,用反证法的思想来说明其可能,对于D,直接判断得分情况,可以说明其可能性.
【详解】
对于A,比如有一位同学得2分,三位同学得10分,其余六位同学都得8分,满足平均数为8,众数为8,但不满足总得分达到70分且没有同学得分低于5分,故A不能保证该班一定为“优胜班级”;
对于B,10位同学的得分可能是:4,6,6,8,8,8,10,10,10,10,此时满足平均数为8,方差为4
但不满足总得分达到70分且没有同学得分低于5分,故B不能保证该班一定为“优胜班级”;
对于C,如果有同学得分低于5分,根据极差为3,那么就,会出现其他同学的得分不大于7,这样平均分就低于7分,不符合丙班同学平均数为7,极差为3的条件,故这种情况下不会有得分低于5分的同学,满足总得分达到70分且没有同学得分低于5分,故C能保证该班一定为“优胜班级”;
对于D, 丁班同学平均数为7,标准差为0,可知每位同学得分均为7分,故D能保证该班一定为“优胜班级”,
故选:CD.
8.AD
【解析】
【分析】
根据选项逐一对相应的统计图进行分析判断即可.
【详解】
对A:由扇形图可知,31~41周岁的参保人数最多,故选项A正确;
对B:由折线图可知,随着年龄的增长人均参保费用越来越多,故选项B错误;
对C:由扇形图可知,30周岁以上的参保人数约占总参保人数的80%,故选项C错误;
对D:由柱状图可知,丁险种参保比例最高,故选项D正确.
故选:AD.
9.甲
【解析】
【详解】
,
又,
,
,所以入选的最佳人选应是甲.
10.3
【解析】
【详解】
分析:由题意结合平均数、方差的性质整理计算即可求得最终结果.
详解:由题意结合平均数和方差的性质可知:
数据,,…,的平均数为:,方差为:,
则平均数和方差之和是.
点睛:本题主要考查均值的性质、方差的性质等知识,意在考查学生的转化能力和计算求解能力.
11.
【解析】
【分析】
根据题意得,,进而解方程即可得答案.
【详解】
解:根据题意得平均数,
方差
即,,解得或,
所以
故答案为:
12.②③④
【解析】
【分析】
根据各个选项,分别分析新增人数的最大值是否可能大于5,即可得结论.
【详解】
仅仅平均值不大于3,有可能其中某个值大于5,①不符合;
平均数时,若7天中有一个数值大于5,则方差,因此在标准差时,7天的数据都不超过5,②符合指标;
平均数且极差小于或等于2,最大值必不大于5,③符合指标;
众数等于1且极差小于或等于4时,最大值必不大于5,否则极差大于6-1=5,④符合指标.
故答案为:②③④
【点睛】
本题考查平均数,标准差,极差,众数等概念,掌握这些概念,能用反证法是解题关键.
13.(1)茎叶图见解析;(2)派乙更合适
【解析】
【分析】
(1)根据茎叶图的画法可画出茎叶图;
(2)利用平均数公式分别求得甲、乙的平均数,利用方差公式分别求得甲、乙的方差,比较平均数与方差的大小,根据平均数与方差的实际意义可得结论.
【详解】
(1)茎叶图如下:
(2)甲的平均数为:=33,
乙的平均数为:(28+29+33+34+36+38)=33,
甲的方差为:,
乙的方差为:,
甲、乙的平均数相等,乙的方差更小,则乙的发挥更稳定,故乙参加比赛更合适.
14.(1);
(2);;
(3)类工人个体间的差异程度更小
【解析】
【分析】
(1)根据分层抽样的概念直接计算;
(2)根据频率分布直方图,利用中位数,众数,平均数的概念及公式直接计算;
(3)根据频率分布直方图直接可得结论.
(1)
解:由已知分层抽样可得:类工人抽取人,类工人抽取人;
(2)
解:中位数:设中位数为,由频率分布直方图可得,,所以,且,解得:,即中位数为;
众数:由频率分布直方图可得众数为;
平均数:,即平均数为;
(3)
根据频率分布直方图可判断类工人个体间的差异程度更小.
15.(1)0.06
(2)172.25
(3)176.25
【解析】
【分析】
(1)利用频率分布直方图中长方形面积之和为1,易求出x;
(2)直接利用平均数公式求出平均数;
(3)可设该校100名生学身高的75%分位数为x,再利用频率分布直方图计算即得
(1)
由频率分布直方图可知5×(0.01+0.07+x+0.04+0.02+0.01)=1,解得x=0.06,
(2)
根据频率分布直方图,由平均数公式可得:
(3)
的人数占比为5×0.02=10%.
的人数占比为5×00.4=20%.
所以该校100名生学身高的75%分位数落在.
设该校100名生学身高的75%分位数为x,则,解得x=176.25.
故该校100名生学身高的75%分位数为176.25.
16.(1),,,;(2)淘汰丙机床,乙机床的性能最好.
【解析】
【分析】
(1)根据平均数,方差的定义求两组数据的平均数和方差;
(2)根据平均数的意义和方差的意义判断三台机床哪台性能最好,哪台性能最差.
【详解】
(1),
,
,
.
(2)因为,,
所以次品数的平均数最小的是乙,稳定性最好的也是乙,稳定性最差的是丙,
故应淘汰丙机床,乙机床的性能最好.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
