2021-2022学年度高一下数学一课一练第九章统计单元测试卷(Word含解析)
文档属性
| 名称 | 2021-2022学年度高一下数学一课一练第九章统计单元测试卷(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 600.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览



文档简介
第九章统计单元测试
一、单选题
1.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
2.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表:分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
甲的成绩
环数 7 8 9 10
频数 5 5 5 5
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 4 6 6 4
A. B. C. D.
3.某班50名学生在一次百米测试中,成绩全部介于13s与19s之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13s且小于14s;第二组,成绩大于等于14s且小于15s;……;第六组,成绩大于等于18s且小于等于19s.如图是按上述分组方法得到的频率分布直方图.设成绩小于17s的学生人数占全班总人数的百分比为,成绩大于等于15s且小于17s的学生人数为,平均成绩为,则从频率分布直方图中可分析出,,的值分别为( )
A.90%,35,15.86 B.90%,45,15.5
C.10%,35,16 D.10%,45,16.8
4.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
5.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A.甲地:总体均值为3,中位数为4 B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3 D.丁地:总体均值为2,总体方差为3
6.某地某年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是
A.计算机行业好于化工行业. B.建筑行业好于物流行业.
C.机械行业最紧张. D.营销行业比贸易行业紧张.
二、多选题
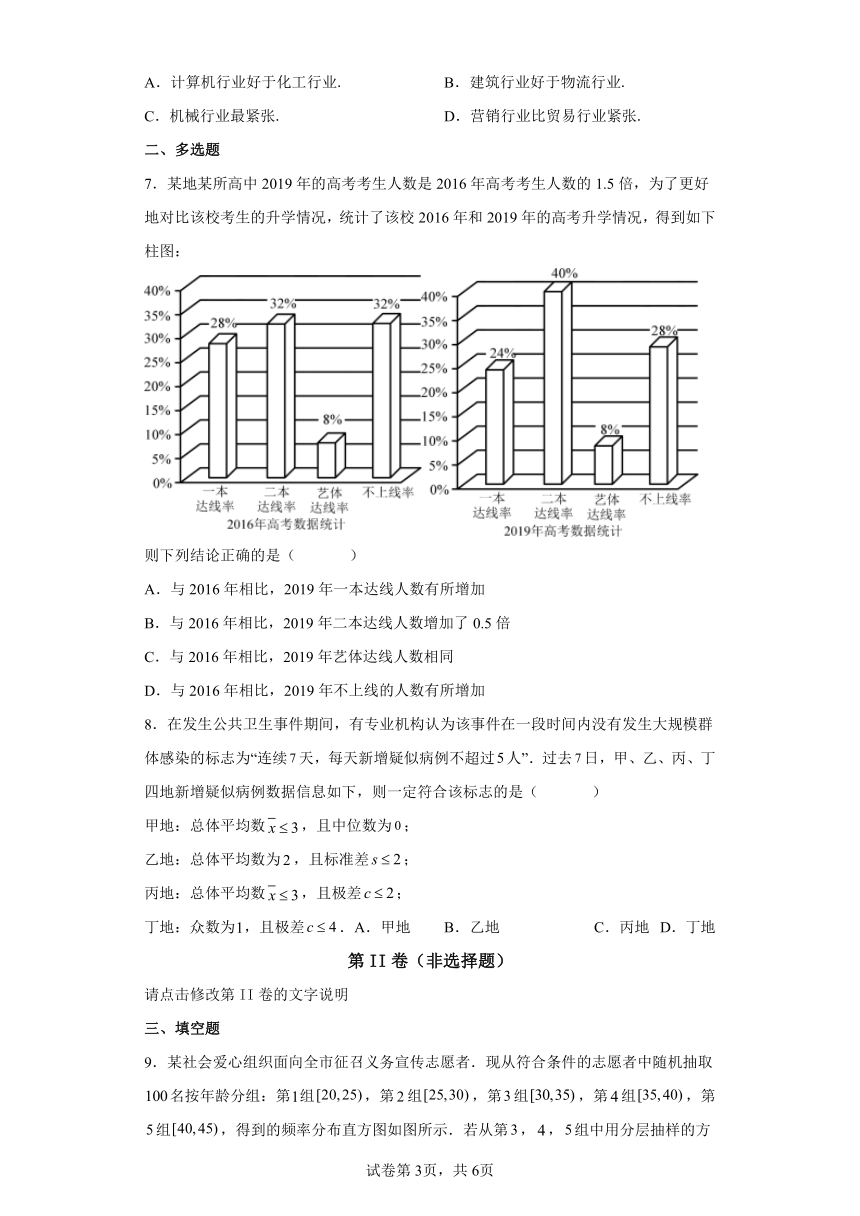
7.某地某所高中2019年的高考考生人数是2016年高考考生人数的1.5倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考升学情况,得到如下柱图:
则下列结论正确的是( )
A.与2016年相比,2019年一本达线人数有所增加
B.与2016年相比,2019年二本达线人数增加了0.5倍
C.与2016年相比,2019年艺体达线人数相同
D.与2016年相比,2019年不上线的人数有所增加
8.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续天,每天新增疑似病例不超过人”.过去日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:总体平均数,且中位数为;
乙地:总体平均数为,且标准差;
丙地:总体平均数,且极差;
丁地:众数为,且极差.A.甲地 B.乙地 C.丙地 D.丁地
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
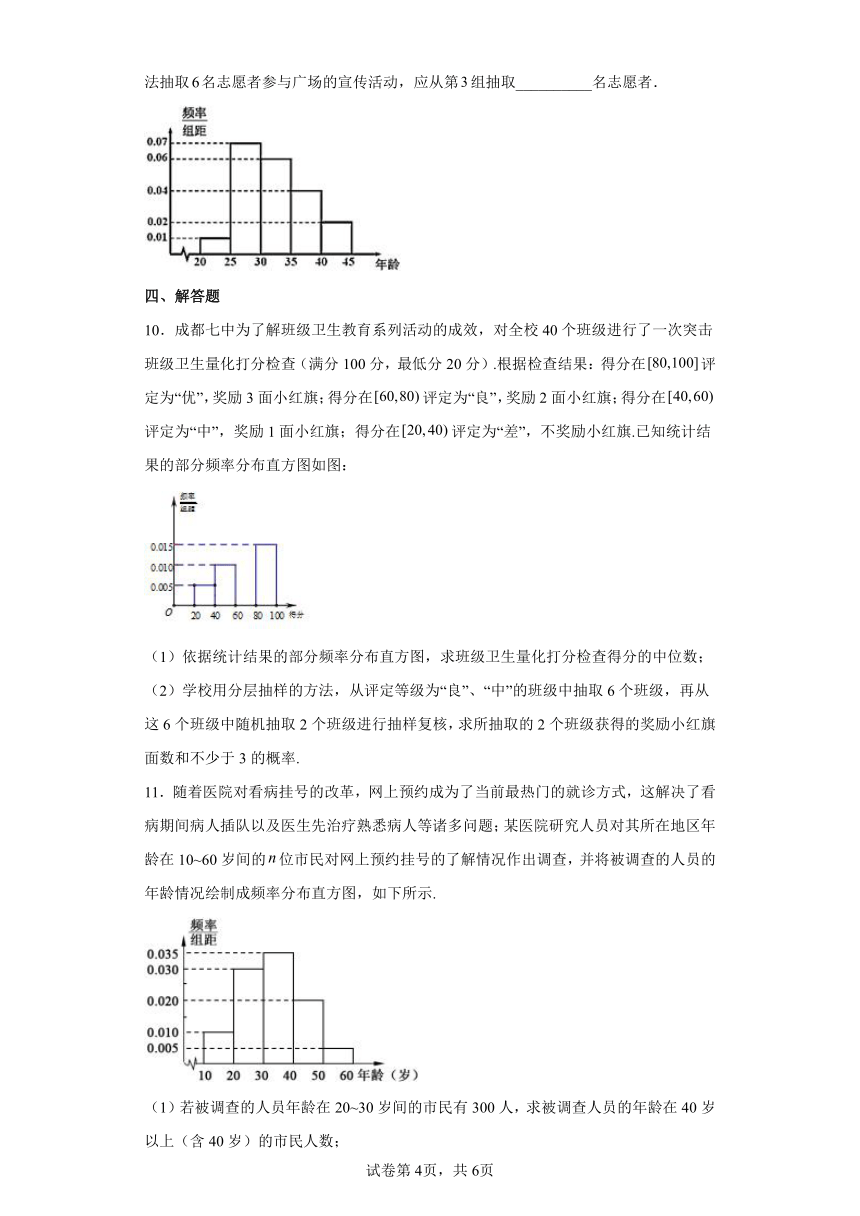
9.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
四、解答题
10.成都七中为了解班级卫生教育系列活动的成效,对全校40个班级进行了一次突击班级卫生量化打分检查(满分100分,最低分20分).根据检查结果:得分在评定为“优”,奖励3面小红旗;得分在评定为“良”,奖励2面小红旗;得分在评定为“中”,奖励1面小红旗;得分在评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如图:
(1)依据统计结果的部分频率分布直方图,求班级卫生量化打分检查得分的中位数;
(2)学校用分层抽样的方法,从评定等级为“良”、“中”的班级中抽取6个班级,再从这6个班级中随机抽取2个班级进行抽样复核,求所抽取的2个班级获得的奖励小红旗面数和不少于3的概率.
11.随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下所示.
(1)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(2)若按分层抽样的方法从年龄在以及内的市民中随机抽取10人,再从这10人中随机抽取3人进行调研,记随机抽取的3人中,年龄在内的人数为,求的分布列以及数学期望.
12.某地区100位居民的人均月用水量(单位:)的分组及各组的频数如下:
,4; ,8; ,15;
,22; ,25; ,14;
,6; ,4; ,2.
(1)列出样本的频率分布表;
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为的标准,若超出标准加倍收费,当地政府说,以上的居民不超过这个标准,这个解释对吗?为什么?
13.为了落实习主席提出“绿水青山就是金山银山”的环境治理要求,某市政府积极鼓励居民节约用水.计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨),一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年200位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2),…,[8,9)分成9组,制成了如图所示的频率分布直方图,其中.
(1)求直方图中的值,并由频率分布直方图估计该市居民用水的平均数(每组数据用该组区间中点值作为代表);
(2)设该市有40万居民,估计全市居民中月均用水量不低于2吨的人数,并说明理由;
(3)若该市政府希望使85%的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
14.某社区名居民参加年国庆活动,他们的年龄在岁至岁之间,将年龄按、、、、分组,得到的频率分布直方图如图所示.
(1)求的值,并求该社区参加年国庆活动的居民的平均年龄(每个分组取中间值作代表);
(2)现从年龄在、的人员中按分层抽样的方法抽取人,再从这人中随机抽取人进行座谈,用表示参与座谈的居民的年龄在的人数,求的分布列和数学期望;
(3)若用样本的频率代替概率,用随机抽样的方法从该地岁至岁之间的市民中抽取名进行调查,其中有名市民的年龄在的概率为,当最大时,求的值.
15.中国女排一直是国人的骄傲,2019年女排世界杯于9月14日﹣9月29日在日本举行,中国女排10连胜提前夺冠,获世界杯第五冠 三大赛第十冠.中国女排用胜利点燃国人的激情,女排精神成为了拼搏 不服输的代表.某校受此影响,也举办了校园排球联赛,每班各自选出12人代表队,最后甲 乙两班进入决赛,如下茎叶图所示的是对每名队员上场时间做的统计,根据茎叶图回答问题:
(1)计算甲 乙两班队员上场的平均时间,并根据茎叶图分析哪班队员上场时间更均衡(不需要计算);
(2)赛后学校在上场时间超过50分钟(包括50分钟)的队员中随机抽取2人评为最佳运动员,则两人中至少有一人来自乙班的概率是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
根据频率分布直方图读出众数a,计算中位数b,平均数c,再比较大小.
【详解】
由频率分布直方图可知:众数;
中位数应落在70-80区间内,则有:,解得:;
平均数
=4.5+8.25+9.75+22.5+21.25+4.75=71
所以
故选:B
【点睛】
从频率分布直方图可以估计出的几个数据:
(1)众数:频率分布直方图中最高矩形的底边中点的横坐标;
(2)平均数:频率分布直方图每组数值的中间值乘以频率后相加;
(3)中位数:把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标.
2.B
【解析】
分别根据平均数和方差公式,计算结果.
【详解】
,
,
,
,
,
,
由,得.
故选:B
【点睛】
结论点睛:本题考查平均数和方差的计算,
1.平均数
2.方差,
3.标准差,
4.平均数大说明样本的平均水平高,方差和标准差大说明样本比较分散,与平均水平差距较大,不稳定.
3.A
【解析】
由频率分布直方图可知每组的频率 ,由此可得的值,根据求平均数为每个小矩形底边中点的横坐标乘以每个小矩形的面积再求和,代入数据即可求解.
【详解】
由频率分布直方图可得,
,,
第一组的频率为,第二组的频率为,第三组的频率为,
第四组的频率为,第五组的频率为,第六组的频率为,
则,
即.
故选:A
【点睛】
本题主要考查利用频率分布直方图估计样本的平均数;从统计图中获取信息是解题的关键;属于中档题.
4.A
【解析】
【分析】
可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】
设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
【点睛】
本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
5.D
【解析】
【详解】
试题分析:由于甲地总体均值为,中位数为,即中间两个数(第天)人数的平均数为,因此后面的人数可以大于,故甲地不符合.乙地中总体均值为,因此这天的感染人数总数为,又由于方差大于,故这天中不可能每天都是,可以有一天大于,故乙地不符合,丙地中中位数为,众数为,出现的最多,并且可以出现,故丙地不符合,故丁地符合.
考点:众数、中位数、平均数、方差
6.B
【解析】
【详解】
∵用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,
∴建筑行业招聘人数是76516,而应聘人数没有排在前五位,小于65280,
建筑行业人才是供不应求,
∵物流行业应聘人数是74570,
而招聘人数不在前五位,要小于70436,
∴物流行业是供大于求,
∴就业形势是建筑行业好于物流行业,
故选B.
7.AD
【解析】
【分析】
根据柱状图给定的信息,作差比较,即可求解.
【详解】
依题意,设2016年高考考生人数为,则2019年高考考生人数为,
由,所以A项正确;
由,所以B项不正确;
由,所以C项不正确;
由,所以D项正确.
故选:AD.
【点睛】
本题主要考查了统计图表的识别和应用,其中解答中熟记柱状图表表示的含义是解答的关键,属于基础题.
8.CD
【解析】
【分析】
根据条件,举例说明甲地和乙地,根据极差的概念,说明每天新增疑似病例的最大值,判断丙地和丁地.
【详解】
甲地:满足总体平均数,且中位数为,举例7天的新增疑似病例为0,0,0,0,5,6,7,则不符合该标志;
乙地:若7天新增疑似病例为1,1,1,1,2,2,6,满足平均数为2,标准差,
但不符合该标志;
丙地:由极差可知,若新增疑似病例最多超过5人,比如6人,那么最小值不低于4人,
那么总体平均数就不正确,故每天新增疑似病例低于5人,故丙地符合该标志;
丁地:因为众数为1,且极差,所以新增疑似病例的最大值,所以丁地符合该标志.
故选:CD
【点睛】
本题考查统计的实际应用,重点考查统计的相关概念,以及举例推理的能力,属于基础题型.
9.
【解析】
【分析】
先分别求出这3组的人数,再利用分层抽样的方法即可得出答案.
【详解】
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
【点睛】
关键点点睛:该题考查的是有关频率分布直方图的识别以及分层抽样某层抽取个数的问题,正确解题的关键是掌握在抽取过程中每个个题被抽到的机会均等.
10.(1)分;(2).
【解析】
(1)利用频率分布直方图,能求出班级卫生量化打分检查得分的中位数.
(2)“良”、“中”的频率分别为0.4,0.2.又班级总数为40.从而“良”、“中”的班级个数分别为16,8.分层抽样的方法抽取的“良”、“中”的班级个数分别为4,2.由此利用对立事件概率计算公式能求出抽取的2个班级获得的奖励小红旗面数和不少于3的概率.
【详解】
(1)得分的频率为;得分的频率为;
得分的频率为;
所以得分的频率为
设班级得分的中位数为分,于是,解得
所以班级卫生量化打分检查得分的中位数为分.
(2)由(1)知题意 “良”、“中”的频率分别为又班级总数为
于是“良”、“中”的班级个数分别为.
分层抽样的方法抽取的“良”、“中”的班级个数分别为
因为评定为“良”,奖励2面小红旗,评定为“中”,奖励1面小红旗.
所以抽取的2个班级获得的奖励小红旗面数和不少于3为两个评定为“良”的班级或一个评定为“良”与一个评定为“中”的班级.记这个事件为
则为两个评定为“中”的班级.
把4个评定为“良”的班级标记为 2个评定为“中”的班级标记为
从这6个班级中随机抽取2个班级用点表示,其中.这些点恰好为方格格点上半部分(不含对角线上的点),于是有种.
事件仅有一个基本事件. 所以
所抽取的2个班级获得的奖励小红旗面数和不少于3的概率为.
【点睛】
本题考查中位数、概率的求法,考查分层抽样、频率分布直方图、古典概型等基础知识,考查运算求解能力,是基础题.
11.(1)250;(2)详见解析.
【解析】
(1)先求出年龄在40岁以上(含40岁)的市民的频率,然后根据比例关系可得人数;
(2)先确定的可能取值,然后分别求解概率,可得分布列和期望.
【详解】
(1)依题意,所求人数为.
(2)依题意,年龄在以内及以内的人中分别抽取6人和4人;
故的可能取值为0,1,2,3;
,,,;
故的分布列为:
0 1 2 3
故.
【点睛】
本题主要考查随机变量的分布列和期望,明确随机变量的可能取值及概率是求解的关键,侧重考查数据处理的核心素养.
12.(1)分布表见解析;(2)直方图见解析;平均数为2.02,中位数为2.02,众数为2.25;(3)政府的解释是正确的,原因见解析.
【解析】
【分析】
(1)根据100位居民的人均月用水量(单位:)的分组及各组的频数列出频率分布表.
(2)根据(1)的频率分布表画出直方图,根据众数、中位数和平均数定义求解.
(3)先算出人均月用水量在以上的居民所占的比例即可.
【详解】
(1)频率分布表如下:
分组 频数 频率
合计
(2)频率分布直方图如图:
众数为:
月用水量在的频率为:,
中位数为:
平均数为:,
(3)人均月用水量在以上的居民所占的比例为
即大约有的居民月用水量在以上,的居民月用水量在以下
因此政府的解释是正确的.
【点睛】
本题主要考查频率分布表,频率分布直方图,数字特征及其应用,还考查了数形结合的思想方法,属于中档题.
13.(1),;4.07(2)35.2万;(3)
【解析】
【分析】
(1)由频率之和为1以及列方程组求得的值,并由频率分布直方图中间值作为代表,计算出平均数;
(2)计算不低于2吨人数对应的频率,求出对应的人数;
(3)由频率分布直方图计算频率,可判断,再根据频率列出方程,求出的值.
【详解】
解:(1)由频率分布直方图可得
,
又,则,,
该市居民用水的平均数估计为:
;
(2)由频率分布直方图可得,
月均用水量不超过2吨的频率为:,
则月均用水量不低于2吨的频率为:,
所以全市40万居民中月均用水量不低于2吨的人数为:
(万);
(3)由频率分布直方图知月均用水量不超过6吨的频率为:0.88,
月均用水量不超过5吨的频率为0.73,
则85%的居民每月的用水量不超过的标准(吨),,
,解得,
即标准为5.8吨.
【点睛】
本题考查了频率分布直方图的应用,求平均数,计算频率,总体百分位数的估计,考查了数据处理能力和运算能力,属于中档题.
14.(1),平均年龄;(2)分布列见解析,;(3).
【解析】
【分析】
(1)由频率分布直方图中所有矩形面积之和为,求出的值,再将所有矩形底边中点值乘以矩形面积,再将所得的数相加即可得出该社区年国庆活动的居民的平均年龄;
(2)先根据分层抽样得知,所抽取的人中,年龄在的抽取人、年龄在的抽取人,可得出随机变量的可能取值为、、,并利用古典概型的概率公式计算出随机变量分别取、、时的概率,列出随机变量的分布列,并利用数学期望公式计算出随机变量的数学期望;
(3)设年龄在的人数为,可知,利用独立重复试验的概率公式得出,分析出数列的单调性,可求出的最大值及对应的的值.
【详解】
(1)由频率分布直方图知,解得,
所以该社区参加年国庆活动的居民的平均年龄为
;
(2)年龄在的人数为,年龄在的人数为.
根据分层抽样,可知年龄在的抽取人、年龄在的抽取人.
所以的可能取值为0,1,2,且,,,
所以的分布列为
所以;
(3)由题可知年龄在内的频率为.
设年龄在的人数为,所以.
.
设,
由得,此时;由得,此时.
所以当时,最大.
【点睛】
本题考查频率分布直方图中平均数的计算、同时也考查了超几何分布列与二项分布的应用,在解题时要弄清随机变量所服从的概率分布类型,考查分析问题和解决问题的能力,属于中等题.
15.(1)甲班队员上场的平均时间31.25,乙班队员上场的平均时间34.5,甲班队员上场时间更均衡;(2).
【解析】
【分析】
(1)由茎叶图中数据直接求平均数.
(2)列举法写出从5人中选出2人的所有情况,再找出至少有一人来自乙班的选法情况,相比即可求概率.
【详解】
解:(Ⅰ)甲班队员上场的平均时间,
乙班队员上场的平均时间.
由茎叶图分析甲班队员上场时间更均衡.
(Ⅱ)上场时间超过50分钟的队员甲班有两人为,,乙班有3人为,,.
则从5人中随机抽取2人的取法有:,,,,,,,,,,
共有10种,至少有一人来自乙班的有9种,
故两人中至少有一人来自乙班的概率.
【点睛】
本题考查茎叶图,平均数,古典概型等,属于基础题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
2.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表:分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
甲的成绩
环数 7 8 9 10
频数 5 5 5 5
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 4 6 6 4
A. B. C. D.
3.某班50名学生在一次百米测试中,成绩全部介于13s与19s之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13s且小于14s;第二组,成绩大于等于14s且小于15s;……;第六组,成绩大于等于18s且小于等于19s.如图是按上述分组方法得到的频率分布直方图.设成绩小于17s的学生人数占全班总人数的百分比为,成绩大于等于15s且小于17s的学生人数为,平均成绩为,则从频率分布直方图中可分析出,,的值分别为( )
A.90%,35,15.86 B.90%,45,15.5
C.10%,35,16 D.10%,45,16.8
4.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
5.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A.甲地:总体均值为3,中位数为4 B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3 D.丁地:总体均值为2,总体方差为3
6.某地某年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是
A.计算机行业好于化工行业. B.建筑行业好于物流行业.
C.机械行业最紧张. D.营销行业比贸易行业紧张.
二、多选题
7.某地某所高中2019年的高考考生人数是2016年高考考生人数的1.5倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考升学情况,得到如下柱图:
则下列结论正确的是( )
A.与2016年相比,2019年一本达线人数有所增加
B.与2016年相比,2019年二本达线人数增加了0.5倍
C.与2016年相比,2019年艺体达线人数相同
D.与2016年相比,2019年不上线的人数有所增加
8.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续天,每天新增疑似病例不超过人”.过去日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:总体平均数,且中位数为;
乙地:总体平均数为,且标准差;
丙地:总体平均数,且极差;
丁地:众数为,且极差.A.甲地 B.乙地 C.丙地 D.丁地
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
9.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
四、解答题
10.成都七中为了解班级卫生教育系列活动的成效,对全校40个班级进行了一次突击班级卫生量化打分检查(满分100分,最低分20分).根据检查结果:得分在评定为“优”,奖励3面小红旗;得分在评定为“良”,奖励2面小红旗;得分在评定为“中”,奖励1面小红旗;得分在评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如图:
(1)依据统计结果的部分频率分布直方图,求班级卫生量化打分检查得分的中位数;
(2)学校用分层抽样的方法,从评定等级为“良”、“中”的班级中抽取6个班级,再从这6个班级中随机抽取2个班级进行抽样复核,求所抽取的2个班级获得的奖励小红旗面数和不少于3的概率.
11.随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下所示.
(1)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(2)若按分层抽样的方法从年龄在以及内的市民中随机抽取10人,再从这10人中随机抽取3人进行调研,记随机抽取的3人中,年龄在内的人数为,求的分布列以及数学期望.
12.某地区100位居民的人均月用水量(单位:)的分组及各组的频数如下:
,4; ,8; ,15;
,22; ,25; ,14;
,6; ,4; ,2.
(1)列出样本的频率分布表;
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为的标准,若超出标准加倍收费,当地政府说,以上的居民不超过这个标准,这个解释对吗?为什么?
13.为了落实习主席提出“绿水青山就是金山银山”的环境治理要求,某市政府积极鼓励居民节约用水.计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨),一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年200位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2),…,[8,9)分成9组,制成了如图所示的频率分布直方图,其中.
(1)求直方图中的值,并由频率分布直方图估计该市居民用水的平均数(每组数据用该组区间中点值作为代表);
(2)设该市有40万居民,估计全市居民中月均用水量不低于2吨的人数,并说明理由;
(3)若该市政府希望使85%的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
14.某社区名居民参加年国庆活动,他们的年龄在岁至岁之间,将年龄按、、、、分组,得到的频率分布直方图如图所示.
(1)求的值,并求该社区参加年国庆活动的居民的平均年龄(每个分组取中间值作代表);
(2)现从年龄在、的人员中按分层抽样的方法抽取人,再从这人中随机抽取人进行座谈,用表示参与座谈的居民的年龄在的人数,求的分布列和数学期望;
(3)若用样本的频率代替概率,用随机抽样的方法从该地岁至岁之间的市民中抽取名进行调查,其中有名市民的年龄在的概率为,当最大时,求的值.
15.中国女排一直是国人的骄傲,2019年女排世界杯于9月14日﹣9月29日在日本举行,中国女排10连胜提前夺冠,获世界杯第五冠 三大赛第十冠.中国女排用胜利点燃国人的激情,女排精神成为了拼搏 不服输的代表.某校受此影响,也举办了校园排球联赛,每班各自选出12人代表队,最后甲 乙两班进入决赛,如下茎叶图所示的是对每名队员上场时间做的统计,根据茎叶图回答问题:
(1)计算甲 乙两班队员上场的平均时间,并根据茎叶图分析哪班队员上场时间更均衡(不需要计算);
(2)赛后学校在上场时间超过50分钟(包括50分钟)的队员中随机抽取2人评为最佳运动员,则两人中至少有一人来自乙班的概率是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
根据频率分布直方图读出众数a,计算中位数b,平均数c,再比较大小.
【详解】
由频率分布直方图可知:众数;
中位数应落在70-80区间内,则有:,解得:;
平均数
=4.5+8.25+9.75+22.5+21.25+4.75=71
所以
故选:B
【点睛】
从频率分布直方图可以估计出的几个数据:
(1)众数:频率分布直方图中最高矩形的底边中点的横坐标;
(2)平均数:频率分布直方图每组数值的中间值乘以频率后相加;
(3)中位数:把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标.
2.B
【解析】
分别根据平均数和方差公式,计算结果.
【详解】
,
,
,
,
,
,
由,得.
故选:B
【点睛】
结论点睛:本题考查平均数和方差的计算,
1.平均数
2.方差,
3.标准差,
4.平均数大说明样本的平均水平高,方差和标准差大说明样本比较分散,与平均水平差距较大,不稳定.
3.A
【解析】
由频率分布直方图可知每组的频率 ,由此可得的值,根据求平均数为每个小矩形底边中点的横坐标乘以每个小矩形的面积再求和,代入数据即可求解.
【详解】
由频率分布直方图可得,
,,
第一组的频率为,第二组的频率为,第三组的频率为,
第四组的频率为,第五组的频率为,第六组的频率为,
则,
即.
故选:A
【点睛】
本题主要考查利用频率分布直方图估计样本的平均数;从统计图中获取信息是解题的关键;属于中档题.
4.A
【解析】
【分析】
可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】
设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
【点睛】
本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
5.D
【解析】
【详解】
试题分析:由于甲地总体均值为,中位数为,即中间两个数(第天)人数的平均数为,因此后面的人数可以大于,故甲地不符合.乙地中总体均值为,因此这天的感染人数总数为,又由于方差大于,故这天中不可能每天都是,可以有一天大于,故乙地不符合,丙地中中位数为,众数为,出现的最多,并且可以出现,故丙地不符合,故丁地符合.
考点:众数、中位数、平均数、方差
6.B
【解析】
【详解】
∵用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,
∴建筑行业招聘人数是76516,而应聘人数没有排在前五位,小于65280,
建筑行业人才是供不应求,
∵物流行业应聘人数是74570,
而招聘人数不在前五位,要小于70436,
∴物流行业是供大于求,
∴就业形势是建筑行业好于物流行业,
故选B.
7.AD
【解析】
【分析】
根据柱状图给定的信息,作差比较,即可求解.
【详解】
依题意,设2016年高考考生人数为,则2019年高考考生人数为,
由,所以A项正确;
由,所以B项不正确;
由,所以C项不正确;
由,所以D项正确.
故选:AD.
【点睛】
本题主要考查了统计图表的识别和应用,其中解答中熟记柱状图表表示的含义是解答的关键,属于基础题.
8.CD
【解析】
【分析】
根据条件,举例说明甲地和乙地,根据极差的概念,说明每天新增疑似病例的最大值,判断丙地和丁地.
【详解】
甲地:满足总体平均数,且中位数为,举例7天的新增疑似病例为0,0,0,0,5,6,7,则不符合该标志;
乙地:若7天新增疑似病例为1,1,1,1,2,2,6,满足平均数为2,标准差,
但不符合该标志;
丙地:由极差可知,若新增疑似病例最多超过5人,比如6人,那么最小值不低于4人,
那么总体平均数就不正确,故每天新增疑似病例低于5人,故丙地符合该标志;
丁地:因为众数为1,且极差,所以新增疑似病例的最大值,所以丁地符合该标志.
故选:CD
【点睛】
本题考查统计的实际应用,重点考查统计的相关概念,以及举例推理的能力,属于基础题型.
9.
【解析】
【分析】
先分别求出这3组的人数,再利用分层抽样的方法即可得出答案.
【详解】
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
【点睛】
关键点点睛:该题考查的是有关频率分布直方图的识别以及分层抽样某层抽取个数的问题,正确解题的关键是掌握在抽取过程中每个个题被抽到的机会均等.
10.(1)分;(2).
【解析】
(1)利用频率分布直方图,能求出班级卫生量化打分检查得分的中位数.
(2)“良”、“中”的频率分别为0.4,0.2.又班级总数为40.从而“良”、“中”的班级个数分别为16,8.分层抽样的方法抽取的“良”、“中”的班级个数分别为4,2.由此利用对立事件概率计算公式能求出抽取的2个班级获得的奖励小红旗面数和不少于3的概率.
【详解】
(1)得分的频率为;得分的频率为;
得分的频率为;
所以得分的频率为
设班级得分的中位数为分,于是,解得
所以班级卫生量化打分检查得分的中位数为分.
(2)由(1)知题意 “良”、“中”的频率分别为又班级总数为
于是“良”、“中”的班级个数分别为.
分层抽样的方法抽取的“良”、“中”的班级个数分别为
因为评定为“良”,奖励2面小红旗,评定为“中”,奖励1面小红旗.
所以抽取的2个班级获得的奖励小红旗面数和不少于3为两个评定为“良”的班级或一个评定为“良”与一个评定为“中”的班级.记这个事件为
则为两个评定为“中”的班级.
把4个评定为“良”的班级标记为 2个评定为“中”的班级标记为
从这6个班级中随机抽取2个班级用点表示,其中.这些点恰好为方格格点上半部分(不含对角线上的点),于是有种.
事件仅有一个基本事件. 所以
所抽取的2个班级获得的奖励小红旗面数和不少于3的概率为.
【点睛】
本题考查中位数、概率的求法,考查分层抽样、频率分布直方图、古典概型等基础知识,考查运算求解能力,是基础题.
11.(1)250;(2)详见解析.
【解析】
(1)先求出年龄在40岁以上(含40岁)的市民的频率,然后根据比例关系可得人数;
(2)先确定的可能取值,然后分别求解概率,可得分布列和期望.
【详解】
(1)依题意,所求人数为.
(2)依题意,年龄在以内及以内的人中分别抽取6人和4人;
故的可能取值为0,1,2,3;
,,,;
故的分布列为:
0 1 2 3
故.
【点睛】
本题主要考查随机变量的分布列和期望,明确随机变量的可能取值及概率是求解的关键,侧重考查数据处理的核心素养.
12.(1)分布表见解析;(2)直方图见解析;平均数为2.02,中位数为2.02,众数为2.25;(3)政府的解释是正确的,原因见解析.
【解析】
【分析】
(1)根据100位居民的人均月用水量(单位:)的分组及各组的频数列出频率分布表.
(2)根据(1)的频率分布表画出直方图,根据众数、中位数和平均数定义求解.
(3)先算出人均月用水量在以上的居民所占的比例即可.
【详解】
(1)频率分布表如下:
分组 频数 频率
合计
(2)频率分布直方图如图:
众数为:
月用水量在的频率为:,
中位数为:
平均数为:,
(3)人均月用水量在以上的居民所占的比例为
即大约有的居民月用水量在以上,的居民月用水量在以下
因此政府的解释是正确的.
【点睛】
本题主要考查频率分布表,频率分布直方图,数字特征及其应用,还考查了数形结合的思想方法,属于中档题.
13.(1),;4.07(2)35.2万;(3)
【解析】
【分析】
(1)由频率之和为1以及列方程组求得的值,并由频率分布直方图中间值作为代表,计算出平均数;
(2)计算不低于2吨人数对应的频率,求出对应的人数;
(3)由频率分布直方图计算频率,可判断,再根据频率列出方程,求出的值.
【详解】
解:(1)由频率分布直方图可得
,
又,则,,
该市居民用水的平均数估计为:
;
(2)由频率分布直方图可得,
月均用水量不超过2吨的频率为:,
则月均用水量不低于2吨的频率为:,
所以全市40万居民中月均用水量不低于2吨的人数为:
(万);
(3)由频率分布直方图知月均用水量不超过6吨的频率为:0.88,
月均用水量不超过5吨的频率为0.73,
则85%的居民每月的用水量不超过的标准(吨),,
,解得,
即标准为5.8吨.
【点睛】
本题考查了频率分布直方图的应用,求平均数,计算频率,总体百分位数的估计,考查了数据处理能力和运算能力,属于中档题.
14.(1),平均年龄;(2)分布列见解析,;(3).
【解析】
【分析】
(1)由频率分布直方图中所有矩形面积之和为,求出的值,再将所有矩形底边中点值乘以矩形面积,再将所得的数相加即可得出该社区年国庆活动的居民的平均年龄;
(2)先根据分层抽样得知,所抽取的人中,年龄在的抽取人、年龄在的抽取人,可得出随机变量的可能取值为、、,并利用古典概型的概率公式计算出随机变量分别取、、时的概率,列出随机变量的分布列,并利用数学期望公式计算出随机变量的数学期望;
(3)设年龄在的人数为,可知,利用独立重复试验的概率公式得出,分析出数列的单调性,可求出的最大值及对应的的值.
【详解】
(1)由频率分布直方图知,解得,
所以该社区参加年国庆活动的居民的平均年龄为
;
(2)年龄在的人数为,年龄在的人数为.
根据分层抽样,可知年龄在的抽取人、年龄在的抽取人.
所以的可能取值为0,1,2,且,,,
所以的分布列为
所以;
(3)由题可知年龄在内的频率为.
设年龄在的人数为,所以.
.
设,
由得,此时;由得,此时.
所以当时,最大.
【点睛】
本题考查频率分布直方图中平均数的计算、同时也考查了超几何分布列与二项分布的应用,在解题时要弄清随机变量所服从的概率分布类型,考查分析问题和解决问题的能力,属于中等题.
15.(1)甲班队员上场的平均时间31.25,乙班队员上场的平均时间34.5,甲班队员上场时间更均衡;(2).
【解析】
【分析】
(1)由茎叶图中数据直接求平均数.
(2)列举法写出从5人中选出2人的所有情况,再找出至少有一人来自乙班的选法情况,相比即可求概率.
【详解】
解:(Ⅰ)甲班队员上场的平均时间,
乙班队员上场的平均时间.
由茎叶图分析甲班队员上场时间更均衡.
(Ⅱ)上场时间超过50分钟的队员甲班有两人为,,乙班有3人为,,.
则从5人中随机抽取2人的取法有:,,,,,,,,,,
共有10种,至少有一人来自乙班的有9种,
故两人中至少有一人来自乙班的概率.
【点睛】
本题考查茎叶图,平均数,古典概型等,属于基础题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
