2.1.2异面直线
图片预览






文档简介
课件15张PPT。2.1.2空间中直线与直线
之间的位置关系(上)湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作复习引入:1.同一平面内不重合两条直线有几种位置关系?2.在同一平面内,同平行于一条直线的两条直线有什么位置关系?(1)相交:有且仅有一个公共点。(2)平行:在同一平面内没有公共点。互相平行提出问题:空间中的两条直线呢?1.空间中两条直线的位置关系观察:观察教室内的日光灯管所在直线与黑板的左右两侧所在的直线,想一想:它们相交吗?平行吗?共面吗?观察长方体的棱所在
直线,回答类似的问题.思考:我们把具有上述特征的两条直线取个怎样的名字才好呢?线段A′B′所在直线与线段CC′所在直线的位置关系如何? 异面直线的定义:我们把不同在任何一个平面内的两条直线叫做异面直线(skew?lines)。空间两条直线的位置关系有且只有三种练习:1、“a,b是异面直线”,则下列命题正确的是
①?a∩b=Φ,且a不平行于b;
②?a 包含于平面α,b包含于平面β,且a∩b=Φ ?
③?a?包含于平面α,b??平面a?
④?不存在平面α,能使a包含于α,且b包含于α成立√√( )2. 两条异面直线指:A. 空间中不相交的两条直线;
B. 某平面内的一条直线和这平面外的直线;
C. 分别在不同平面内的两条直线;
D. 不在同一平面内的两条直线;
E. 不同在任一平面内的两条直线;
F. 分别在两个不同平面内的两条直线;
G. 某一平面内的一条直线和这个平面外
的一条直线;
H. 空间没有公共点的两条直线;
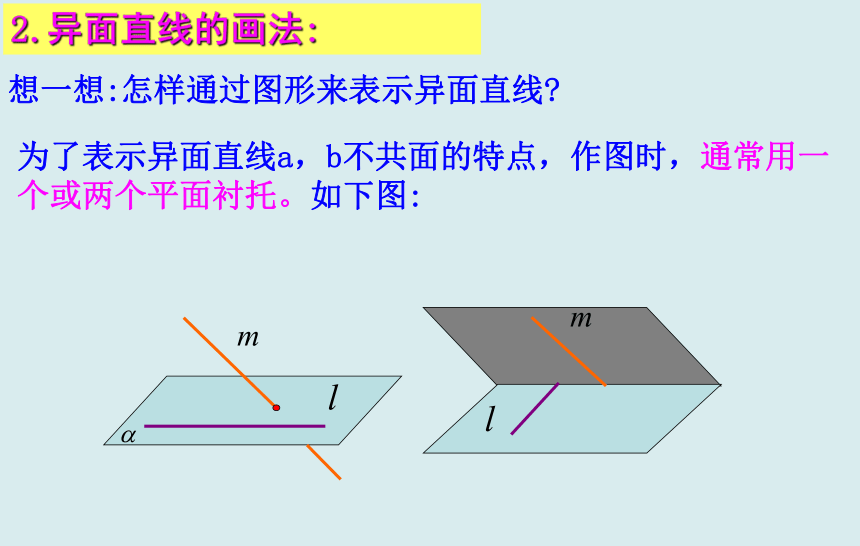
I. 既不相交,又不平行的两条直线.练习:E、I想一想:怎样通过图形来表示异面直线?为了表示异面直线a,b不共面的特点,作图时,通常用一个或两个平面衬托。如下图:2.异面直线的画法: 画两个相交平面,在这两个平面内各画
一条直线,使它们成为:
⑴平行直线;⑵相交直线;⑶异面直线.a??ab??ab??⑴⑵⑶练一练,画一画: 按是否在
同一平面内分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点:按公共点个数分相交直线无公共点平行直线异面直线空间直线与直线之间的位置关系答案:D1C1、C1C、CD、
D1D、AD、B1C1A1B1C1D1CBDA练习 1、如图所示:正方体的棱所在的直线
中,与直线A1B异面的有哪些? 2. 下图是一个正方体的展开图,如果将它还原成正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有几对?探究:三对AB与CD
AB与GH
EF与GH3.想一想,做一做:3、已知M、N分别是长方体的棱C1D1与CC1上的点,那么MN与AB所在的直线是异面直线吗?
3、异面直线的判定方法:(见异面直线的证明专题练习)(1)定义法:由定义判定两直线不可能在同一平面内.(借助反证法)
(2)排除法:既不平行, 也不相交。(3)判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.与 l 是异面直线典型例题讲解已知平面 与平面 相交于直线 , ,为直线 上的两点.在 内作直线 ,在 内作直线 .求证 和 是异面直线.
用定义证明(即定义法):此时需借反证法,假设两条直线不异面,根据空间两条直线的位置关系,这两条直线一定共面,即这两条直线可能相交也可能平行,然后,推导出矛盾即可.
说明:证明两条直线为异面直线,用反证法往往比较简单。
如图,已知不共面的直线 ,,相交于点 , 、 是直线 上两点, 、分别是 ,上一点. 求证: 和 是异面直线.注意:证明两条直线为异面直线,还可用异面直线的判定定理来证明.用定理证明(即定理法):用该法证明时,必须阐述出定理满足的条件:
,,,然后可以推导出直线与是异面直线.课堂小结:作业布置:
P51 A组3、4(1)(2)(4)(5)、 5.
之间的位置关系(上)湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作复习引入:1.同一平面内不重合两条直线有几种位置关系?2.在同一平面内,同平行于一条直线的两条直线有什么位置关系?(1)相交:有且仅有一个公共点。(2)平行:在同一平面内没有公共点。互相平行提出问题:空间中的两条直线呢?1.空间中两条直线的位置关系观察:观察教室内的日光灯管所在直线与黑板的左右两侧所在的直线,想一想:它们相交吗?平行吗?共面吗?观察长方体的棱所在
直线,回答类似的问题.思考:我们把具有上述特征的两条直线取个怎样的名字才好呢?线段A′B′所在直线与线段CC′所在直线的位置关系如何? 异面直线的定义:我们把不同在任何一个平面内的两条直线叫做异面直线(skew?lines)。空间两条直线的位置关系有且只有三种练习:1、“a,b是异面直线”,则下列命题正确的是
①?a∩b=Φ,且a不平行于b;
②?a 包含于平面α,b包含于平面β,且a∩b=Φ ?
③?a?包含于平面α,b??平面a?
④?不存在平面α,能使a包含于α,且b包含于α成立√√( )2. 两条异面直线指:A. 空间中不相交的两条直线;
B. 某平面内的一条直线和这平面外的直线;
C. 分别在不同平面内的两条直线;
D. 不在同一平面内的两条直线;
E. 不同在任一平面内的两条直线;
F. 分别在两个不同平面内的两条直线;
G. 某一平面内的一条直线和这个平面外
的一条直线;
H. 空间没有公共点的两条直线;
I. 既不相交,又不平行的两条直线.练习:E、I想一想:怎样通过图形来表示异面直线?为了表示异面直线a,b不共面的特点,作图时,通常用一个或两个平面衬托。如下图:2.异面直线的画法: 画两个相交平面,在这两个平面内各画
一条直线,使它们成为:
⑴平行直线;⑵相交直线;⑶异面直线.a??ab??ab??⑴⑵⑶练一练,画一画: 按是否在
同一平面内分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点:按公共点个数分相交直线无公共点平行直线异面直线空间直线与直线之间的位置关系答案:D1C1、C1C、CD、
D1D、AD、B1C1A1B1C1D1CBDA练习 1、如图所示:正方体的棱所在的直线
中,与直线A1B异面的有哪些? 2. 下图是一个正方体的展开图,如果将它还原成正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有几对?探究:三对AB与CD
AB与GH
EF与GH3.想一想,做一做:3、已知M、N分别是长方体的棱C1D1与CC1上的点,那么MN与AB所在的直线是异面直线吗?
3、异面直线的判定方法:(见异面直线的证明专题练习)(1)定义法:由定义判定两直线不可能在同一平面内.(借助反证法)
(2)排除法:既不平行, 也不相交。(3)判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.与 l 是异面直线典型例题讲解已知平面 与平面 相交于直线 , ,为直线 上的两点.在 内作直线 ,在 内作直线 .求证 和 是异面直线.
用定义证明(即定义法):此时需借反证法,假设两条直线不异面,根据空间两条直线的位置关系,这两条直线一定共面,即这两条直线可能相交也可能平行,然后,推导出矛盾即可.
说明:证明两条直线为异面直线,用反证法往往比较简单。
如图,已知不共面的直线 ,,相交于点 , 、 是直线 上两点, 、分别是 ,上一点. 求证: 和 是异面直线.注意:证明两条直线为异面直线,还可用异面直线的判定定理来证明.用定理证明(即定理法):用该法证明时,必须阐述出定理满足的条件:
,,,然后可以推导出直线与是异面直线.课堂小结:作业布置:
P51 A组3、4(1)(2)(4)(5)、 5.
