二次函数与实际问题
图片预览




文档简介
课件22张PPT。实际问题与二次函数广水市城郊中心中学2.顶点式y=a(x-h)2+k (a≠0)
1.一般式y=ax2+bx+c (a≠0)3.双根式y=a(x-x1)(x-x2) (a≠0)
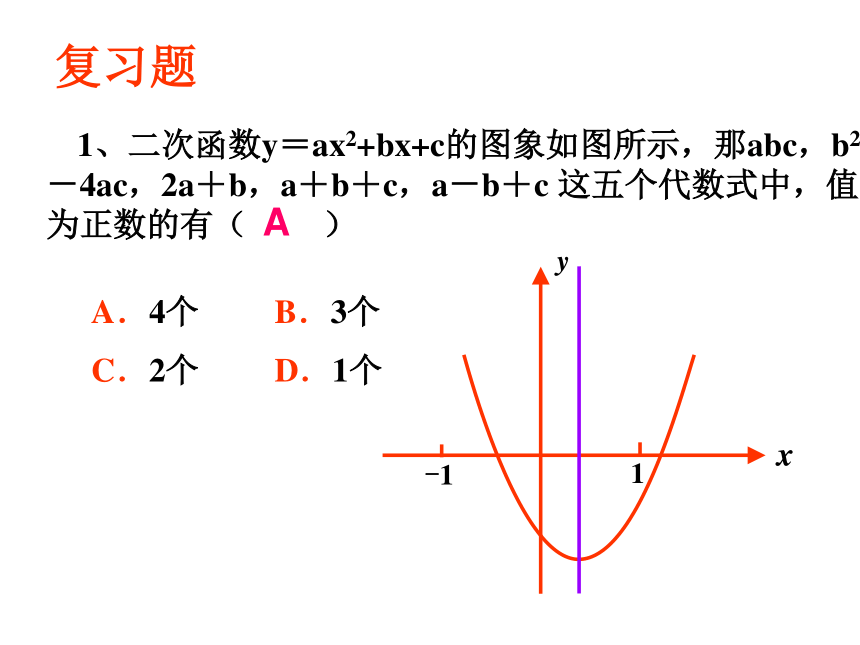
二次函数的三种解析式1、二次函数y=ax2+bx+c的图象如图所示,那abc,b2-4ac,2a+b,a+b+c,a-b+c 这五个代数式中,值为正数的有( )复习题A.4个 B.3个
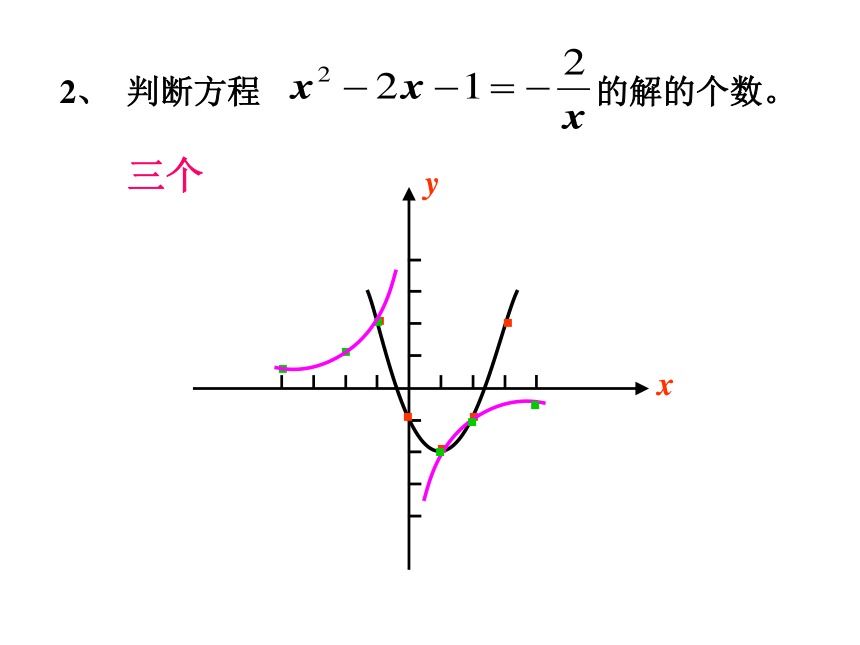
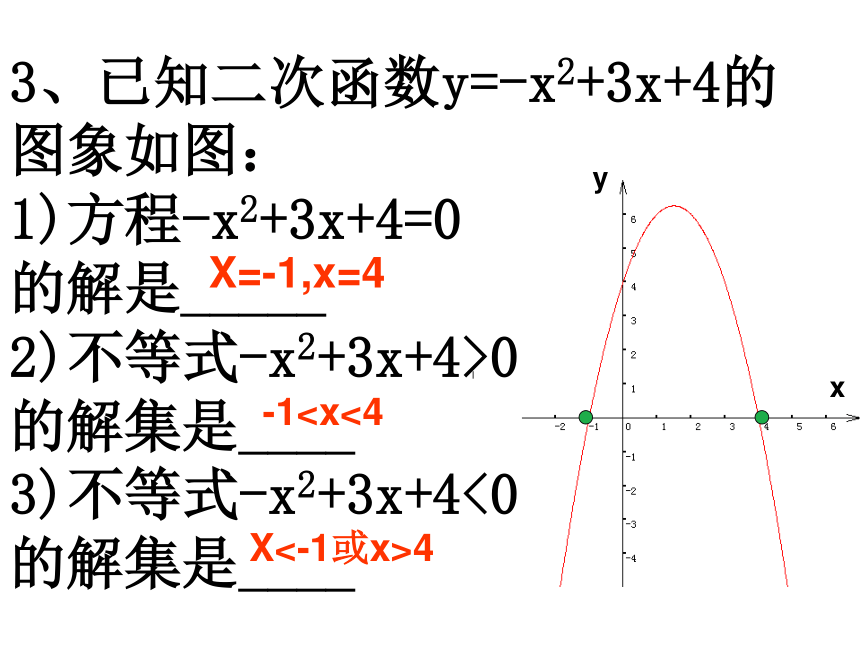
C.2个 D.1个A····2、 判断方程 的解的个数。 ·······三个3、已知二次函数y=-x2+3x+4的图象如图:
1)方程-x2+3x+4=0
的解是_____
2)不等式-x2+3x+4>0
的解集是____
3)不等式-x2+3x+4<0
的解集是____X=-1,x=4X<-1或x>4
-1(2,0),(0,2),求抛物线的解析式解:设抛物线的解析式为y=ax2+c(a≠0)
因为抛物线过(2,0),(0,2)
所以 c=2 a=-0.5
4a+c=0 c=2
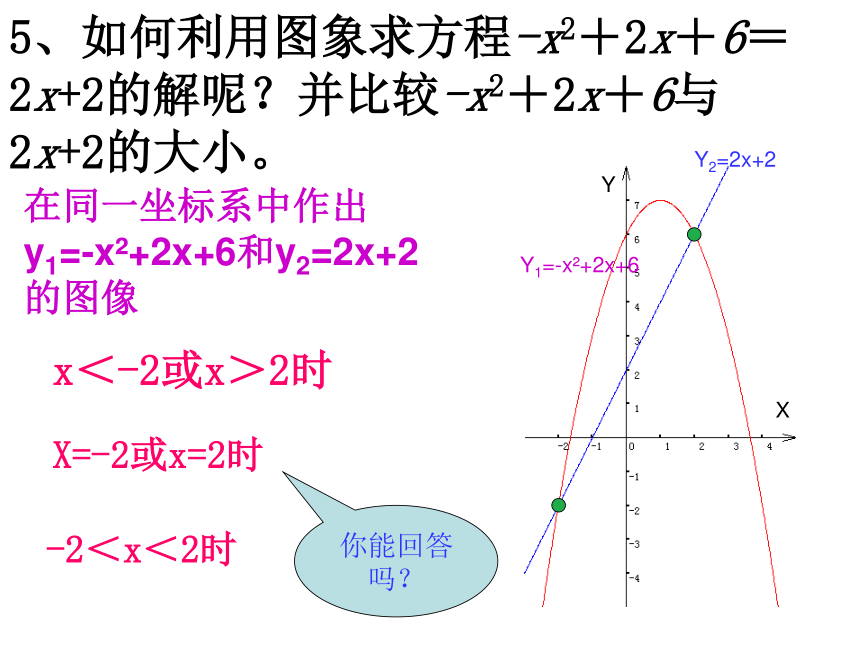
∴解析式为:y=-0.5x2+25、如何利用图象求方程-x2+2x+6=2x+2的解呢?并比较-x2+2x+6与2x+2的大小。x<-2或x>2时X=-2或x=2时-2<x<2时在同一坐标系中作出
y1=-x2+2x+6和y2=2x+2
的图像Y1=-x2+2x+6Y2=2x+2Y
X
你能回答吗? 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?请大家带着以下几个问题读题(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
探究1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?分析:调整价格包括涨价和降价两种情况先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品的利润y也随之变化,我们先来确定y与x的函数关系式。涨价x元时则每星期少卖 件,实际卖出 件,每件利润为 元,因此,所得利润为 元10x(300-10x)(60+x-40)(60+x-40)(300-10x)y=(60+x-40)(300-10x)(0≤X≤30)即y=-10(x-5)2+6250∴当x=5时,y最大值=6250怎样确定x的取值范围所以,当定价为65元时,利润最大,最大利润为6250元也可以这样求极值在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案。解:设降价x元时利润最大,则每星期可多卖20x件,实际卖出(300+20x)件,每件利润为(60-40-x)元,因此,得利润由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗?y=(300+20x)(60-40-x)
=-20(x2-5x+6.25)+6150
=-20(x-2.5)2+6150∴x=2.5时,y极大值=6150你能回答了吧!怎样确定x的取值范围(0<x<20)
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。解这类题目的一般步骤
练习.某商店购进一种单价为40元的篮球,如
果以单价50元售出,那么每月可售出500个,
据销售经验,售价每提高1元,销售量相应减
少10个。 (1)假设销售单价提高x元,那么销售每个
篮球所获得的利润是_______元,这种篮球每
月的销售量是______ 个(用X的代数式表示) (2)8000元是否为每月销售篮球的最大利润?
如果是,说明理由,如果不是,请求出最大利润,
此时篮球的售价应定为多少元?探究2计算机把数据存储在磁盘上,磁盘是带有磁性物质的圆盘,磁盘上有一些同心圆轨道,叫做磁道,现有一张半径为45mm的磁盘,
(1)磁盘最内磁道的半径为rmm,其上每0.015mm的弧长为一个存储单元,这条磁道有多少个存储单元?
(2)磁盘上各磁道之间的宽度必须不小于0.3mm,磁盘的外圆周不是磁道,这张磁盘最多有多少条磁道?
(3)如果各磁道的存储单元数目与最内磁道相同,最内磁道的半径r是多少时,磁盘的存储量最大?即y = (45r-r)2 (0<r<45)你能说出r为多少时y最大吗?一座抛物线形拱桥,当水面
在ι时,拱顶离水面2m,
水面宽4m。水面下降1m,
水面宽度增加多少?探究3如何建立坐标系呢?ACBD你认为A、B、C、D四点,哪一点作为原点
较好?X轴、y轴怎么规定呢?我们来比较一下(0、0)(4、0)(2、2)(-2、-2)(2、-2)(0、0)(-2、0)(2、0)(0、2)(-4、0)(0、0)(-2、2)谁最合适还是都来做一做(0、0)(4、0)(2、2)设抛物线的解析式为
Y=a(x-2)2+2
或y=a(x-0)(x-4)
∴y=-0.5x2+2x设抛物线的解析式为
Y=a(x-0)2+2
或y=a(x+2)(x-2)
∴y=-0.5x2+2(-2、0)(2、0)(0、2)xyxyoo还是都来做一做(0、0)(-2、-2)(2、-2)设抛物线的解析式为
Y=ax2
∴y=-0.5x2(-4、0)(0、0)(-2、2)设抛物线的解析式为
Y=a(x+2)2+2
或y=a(x+4)(x-0)
∴y=-0.5x2-2xoX
Y
O
Y
X
好像是选它最好!X
Y
o解:设抛物线的解析式为
Y=ax2
∵点(2、-2)在抛物线上,
∴a=-0.5 ,
∴这条抛物线的解析式为
y=-0.5x2,
当水面下降1m时,y=-3,
这时有 -3=-0.5x2
解得 x1= 、x2=- 。(-2、-2)(2、-2)(0、0)此时水面宽为2 , 故水面宽增加了(2 -4)m。2 m4m试一试
如图所示,有一座抛物线型拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线型拱桥的解析式。
(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,
在持续多少小时才能达
到拱桥顶?
(3)若正常水位时,有一艘
宽8米,高2.5米的小船
能否安全通过这座桥?实际问题抽象转化数学问题运用数学知识问题的解决谈谈你的学习体会
解题步骤:
1、分析题意,把实际问题转化为数学问题,画出图形。
2、根据已知条件建立适当的平面直角坐标系。
3、选用适当的解析式求解。
4、根据二次函数的解析式解决具体的实际问题。
1.一般式y=ax2+bx+c (a≠0)3.双根式y=a(x-x1)(x-x2) (a≠0)
二次函数的三种解析式1、二次函数y=ax2+bx+c的图象如图所示,那abc,b2-4ac,2a+b,a+b+c,a-b+c 这五个代数式中,值为正数的有( )复习题A.4个 B.3个
C.2个 D.1个A····2、 判断方程 的解的个数。 ·······三个3、已知二次函数y=-x2+3x+4的图象如图:
1)方程-x2+3x+4=0
的解是_____
2)不等式-x2+3x+4>0
的解集是____
3)不等式-x2+3x+4<0
的解集是____X=-1,x=4X<-1或x>4
-1
因为抛物线过(2,0),(0,2)
所以 c=2 a=-0.5
4a+c=0 c=2
∴解析式为:y=-0.5x2+25、如何利用图象求方程-x2+2x+6=2x+2的解呢?并比较-x2+2x+6与2x+2的大小。x<-2或x>2时X=-2或x=2时-2<x<2时在同一坐标系中作出
y1=-x2+2x+6和y2=2x+2
的图像Y1=-x2+2x+6Y2=2x+2Y
X
你能回答吗? 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?请大家带着以下几个问题读题(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
探究1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?分析:调整价格包括涨价和降价两种情况先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品的利润y也随之变化,我们先来确定y与x的函数关系式。涨价x元时则每星期少卖 件,实际卖出 件,每件利润为 元,因此,所得利润为 元10x(300-10x)(60+x-40)(60+x-40)(300-10x)y=(60+x-40)(300-10x)(0≤X≤30)即y=-10(x-5)2+6250∴当x=5时,y最大值=6250怎样确定x的取值范围所以,当定价为65元时,利润最大,最大利润为6250元也可以这样求极值在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案。解:设降价x元时利润最大,则每星期可多卖20x件,实际卖出(300+20x)件,每件利润为(60-40-x)元,因此,得利润由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗?y=(300+20x)(60-40-x)
=-20(x2-5x+6.25)+6150
=-20(x-2.5)2+6150∴x=2.5时,y极大值=6150你能回答了吧!怎样确定x的取值范围(0<x<20)
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。解这类题目的一般步骤
练习.某商店购进一种单价为40元的篮球,如
果以单价50元售出,那么每月可售出500个,
据销售经验,售价每提高1元,销售量相应减
少10个。 (1)假设销售单价提高x元,那么销售每个
篮球所获得的利润是_______元,这种篮球每
月的销售量是______ 个(用X的代数式表示) (2)8000元是否为每月销售篮球的最大利润?
如果是,说明理由,如果不是,请求出最大利润,
此时篮球的售价应定为多少元?探究2计算机把数据存储在磁盘上,磁盘是带有磁性物质的圆盘,磁盘上有一些同心圆轨道,叫做磁道,现有一张半径为45mm的磁盘,
(1)磁盘最内磁道的半径为rmm,其上每0.015mm的弧长为一个存储单元,这条磁道有多少个存储单元?
(2)磁盘上各磁道之间的宽度必须不小于0.3mm,磁盘的外圆周不是磁道,这张磁盘最多有多少条磁道?
(3)如果各磁道的存储单元数目与最内磁道相同,最内磁道的半径r是多少时,磁盘的存储量最大?即y = (45r-r)2 (0<r<45)你能说出r为多少时y最大吗?一座抛物线形拱桥,当水面
在ι时,拱顶离水面2m,
水面宽4m。水面下降1m,
水面宽度增加多少?探究3如何建立坐标系呢?ACBD你认为A、B、C、D四点,哪一点作为原点
较好?X轴、y轴怎么规定呢?我们来比较一下(0、0)(4、0)(2、2)(-2、-2)(2、-2)(0、0)(-2、0)(2、0)(0、2)(-4、0)(0、0)(-2、2)谁最合适还是都来做一做(0、0)(4、0)(2、2)设抛物线的解析式为
Y=a(x-2)2+2
或y=a(x-0)(x-4)
∴y=-0.5x2+2x设抛物线的解析式为
Y=a(x-0)2+2
或y=a(x+2)(x-2)
∴y=-0.5x2+2(-2、0)(2、0)(0、2)xyxyoo还是都来做一做(0、0)(-2、-2)(2、-2)设抛物线的解析式为
Y=ax2
∴y=-0.5x2(-4、0)(0、0)(-2、2)设抛物线的解析式为
Y=a(x+2)2+2
或y=a(x+4)(x-0)
∴y=-0.5x2-2xoX
Y
O
Y
X
好像是选它最好!X
Y
o解:设抛物线的解析式为
Y=ax2
∵点(2、-2)在抛物线上,
∴a=-0.5 ,
∴这条抛物线的解析式为
y=-0.5x2,
当水面下降1m时,y=-3,
这时有 -3=-0.5x2
解得 x1= 、x2=- 。(-2、-2)(2、-2)(0、0)此时水面宽为2 , 故水面宽增加了(2 -4)m。2 m4m试一试
如图所示,有一座抛物线型拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线型拱桥的解析式。
(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,
在持续多少小时才能达
到拱桥顶?
(3)若正常水位时,有一艘
宽8米,高2.5米的小船
能否安全通过这座桥?实际问题抽象转化数学问题运用数学知识问题的解决谈谈你的学习体会
解题步骤:
1、分析题意,把实际问题转化为数学问题,画出图形。
2、根据已知条件建立适当的平面直角坐标系。
3、选用适当的解析式求解。
4、根据二次函数的解析式解决具体的实际问题。
