指数函数
图片预览






文档简介
课件19张PPT。 指数函数 教材分析
知识目标:理解指数函数的概念及其应用
能力目标:培养学生应用数形结合的数学思想,观察问题分析问题的能力,提高学生归纳、总结的能力
情感目标:培养学生唯物主义思想观。通过学生自己归纳总结概念性质增强自信心。教材分析教学重点、难点
通过引例理解指数函数的概念,能对照函数图像分析函数的性质,这是本节课的重点,难点是能灵活运用函数的性质解决问题教学方法和手段教学方法:本节课主要采用问答式教学和讨论探究式教学。教师在教学过程中起到带路人向导的作用,让学生参与到知识形成的全过程。
教学手段:主要采用多媒体教学引例1:某种细胞分裂时,由1个分裂成2个,
2个分裂成4个,……. 1个这样的细胞分裂 x
次后,得到的细胞个数 y 与 x 的函数关系是
什么?分裂次数:1,2,3,4,…,x
细胞个数:2,4,8,16,…,y由上面的对应关系可知,函数关系是.教学程序一、新课导入在,中指数x是自变量,底数是一个大于0且不等于1的常量. 我们把这种自变量在指数位置上而底数是一个
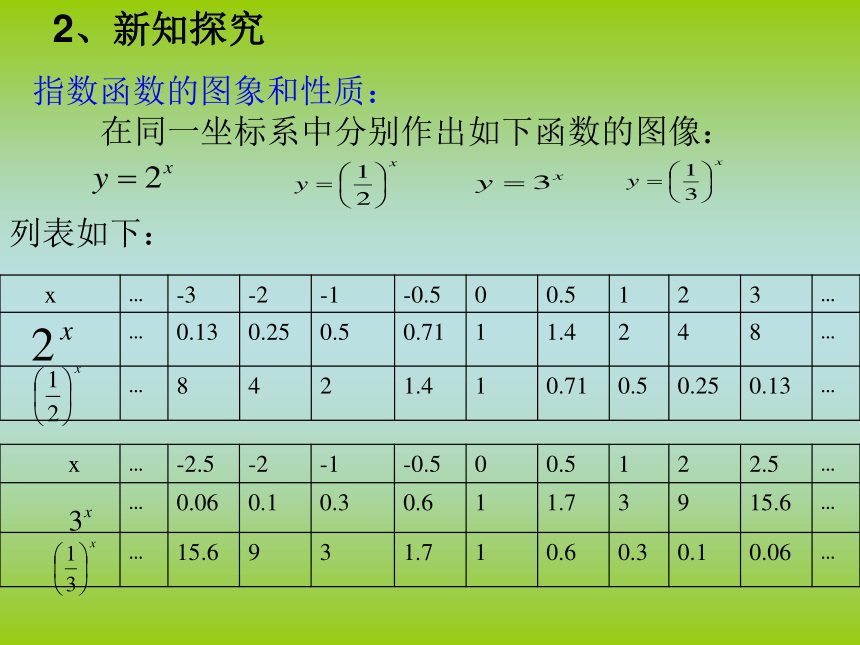
大于0且不等于1的常量的函数叫做指数函数.指数函数的定义: 函数叫做指数函数,其中x是自变量,函数定义域是R。指数函数的图象和性质:在同一坐标系中分别作出如下函数的图像: 列表如下:2、新知探究( )( )( )的图象和性质: 3、归纳总结设计练习,巩固新知 例1某种放射性物质不断变化为其他物质,每经过1年
剩留的这种物质是原来的84%,画出这种物质的剩留
量随时间变化的图象,并从图象上求出经过多少年,
剩量留是原来的一半(结果保留1个有效数字)。分析:通过恰当假设,将剩留量y表示成经过年数x的
函数,并可列表、描点、作图,进而求得所求。解:设这种物质量初的质量是1,经过x年,剩留量是y。经过1年,剩留量经过2年,剩留量……一般地,经过x年,剩留量根据这个函数 可以列表如下: 用描点法画出指数函数 的图象: 从图上看出y=0.5
只需x≈4. 答:约经过4年,
剩留量是原来的
一半。例2 比较下列各题中两个值的大小:①,解① :利用函数单调性与的底数是1.7,它们可以看成函数 y=因为1.7>1,所以函数y=在R上是增函数,而2.5<3,
所以,<;当x=2.5和3时的函数值; ②, 解② :利用函数单调性与的底数是0.8,它们可以看成函数 y= 当x=-0.1和-0.2时的函数值; 因为0<0.8<1,所以函数y=在R是减函数, 而-0.1>-0.2,所以, < 练习:⑴比较大小: , 解:因为利用函数单调性练习:⑵已知下列不等式,试比较m、n的大小:⑶比较下列各数的大小: 小结: 函数叫做指数函数,其中x是自变量,函数定义域是R。1.指数函数的定义: 2.指数函数的的图象和性质:课后作业: P73 习题 2.6 1,2,3
知识目标:理解指数函数的概念及其应用
能力目标:培养学生应用数形结合的数学思想,观察问题分析问题的能力,提高学生归纳、总结的能力
情感目标:培养学生唯物主义思想观。通过学生自己归纳总结概念性质增强自信心。教材分析教学重点、难点
通过引例理解指数函数的概念,能对照函数图像分析函数的性质,这是本节课的重点,难点是能灵活运用函数的性质解决问题教学方法和手段教学方法:本节课主要采用问答式教学和讨论探究式教学。教师在教学过程中起到带路人向导的作用,让学生参与到知识形成的全过程。
教学手段:主要采用多媒体教学引例1:某种细胞分裂时,由1个分裂成2个,
2个分裂成4个,……. 1个这样的细胞分裂 x
次后,得到的细胞个数 y 与 x 的函数关系是
什么?分裂次数:1,2,3,4,…,x
细胞个数:2,4,8,16,…,y由上面的对应关系可知,函数关系是.教学程序一、新课导入在,中指数x是自变量,底数是一个大于0且不等于1的常量. 我们把这种自变量在指数位置上而底数是一个
大于0且不等于1的常量的函数叫做指数函数.指数函数的定义: 函数叫做指数函数,其中x是自变量,函数定义域是R。指数函数的图象和性质:在同一坐标系中分别作出如下函数的图像: 列表如下:2、新知探究( )( )( )的图象和性质: 3、归纳总结设计练习,巩固新知 例1某种放射性物质不断变化为其他物质,每经过1年
剩留的这种物质是原来的84%,画出这种物质的剩留
量随时间变化的图象,并从图象上求出经过多少年,
剩量留是原来的一半(结果保留1个有效数字)。分析:通过恰当假设,将剩留量y表示成经过年数x的
函数,并可列表、描点、作图,进而求得所求。解:设这种物质量初的质量是1,经过x年,剩留量是y。经过1年,剩留量经过2年,剩留量……一般地,经过x年,剩留量根据这个函数 可以列表如下: 用描点法画出指数函数 的图象: 从图上看出y=0.5
只需x≈4. 答:约经过4年,
剩留量是原来的
一半。例2 比较下列各题中两个值的大小:①,解① :利用函数单调性与的底数是1.7,它们可以看成函数 y=因为1.7>1,所以函数y=在R上是增函数,而2.5<3,
所以,<;当x=2.5和3时的函数值; ②, 解② :利用函数单调性与的底数是0.8,它们可以看成函数 y= 当x=-0.1和-0.2时的函数值; 因为0<0.8<1,所以函数y=在R是减函数, 而-0.1>-0.2,所以, < 练习:⑴比较大小: , 解:因为利用函数单调性练习:⑵已知下列不等式,试比较m、n的大小:⑶比较下列各数的大小: 小结: 函数叫做指数函数,其中x是自变量,函数定义域是R。1.指数函数的定义: 2.指数函数的的图象和性质:课后作业: P73 习题 2.6 1,2,3
