2021-2022学年高一下学期物理人教版(2019)必修第二册6.3《向心加速度》课件(18张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期物理人教版(2019)必修第二册6.3《向心加速度》课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-23 10:16:57 | ||
图片预览

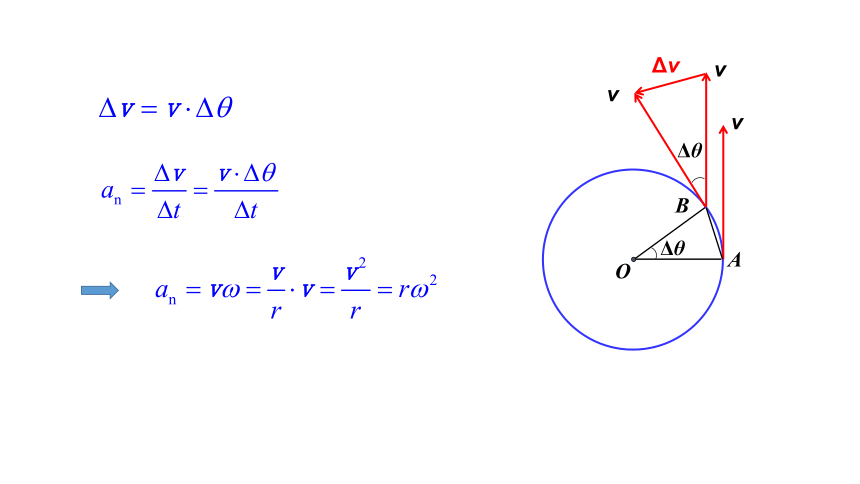

文档简介
(共18张PPT)
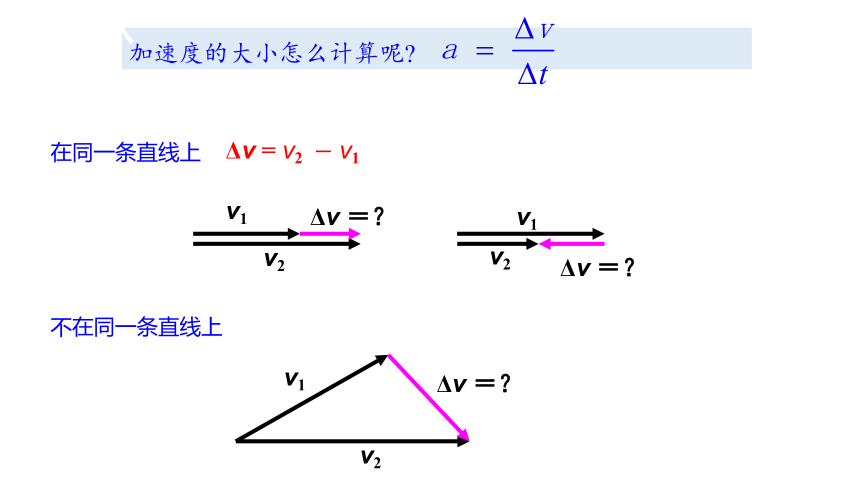
加速度的大小怎么计算呢
在同一条直线上
v1
v2
Δv =?
v1
v2
Δv =?
v1
v2
Δv =?
不在同一条直线上
Δv = v2 v1
新课入
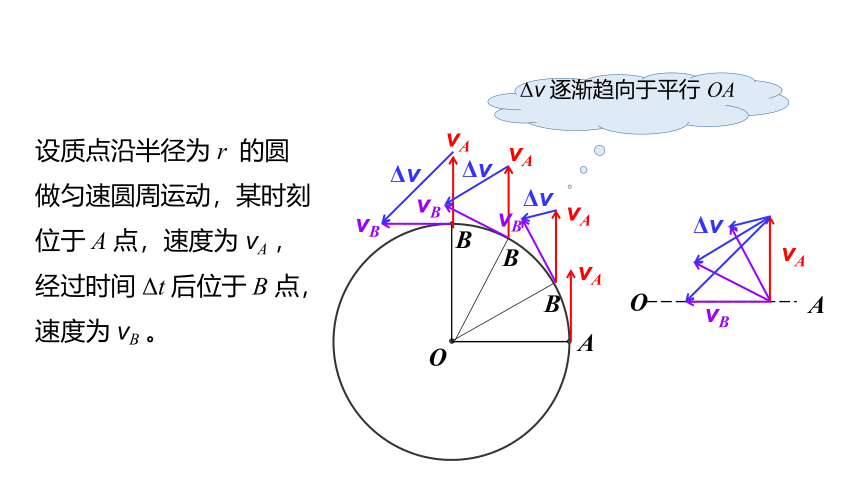
设质点沿半径为 r 的圆做匀速圆周运动,某时刻位于 A 点,速度为 vA ,经过时间 Δt 后位于 B 点,速度为 vB 。
Δv
O
A
B
vB
vA
Δv
B
vB
vA
Δv
B
vB
vA
vA
Δv
vB
vA
A
O
Δv 逐渐趋向于平行 OA
新课入
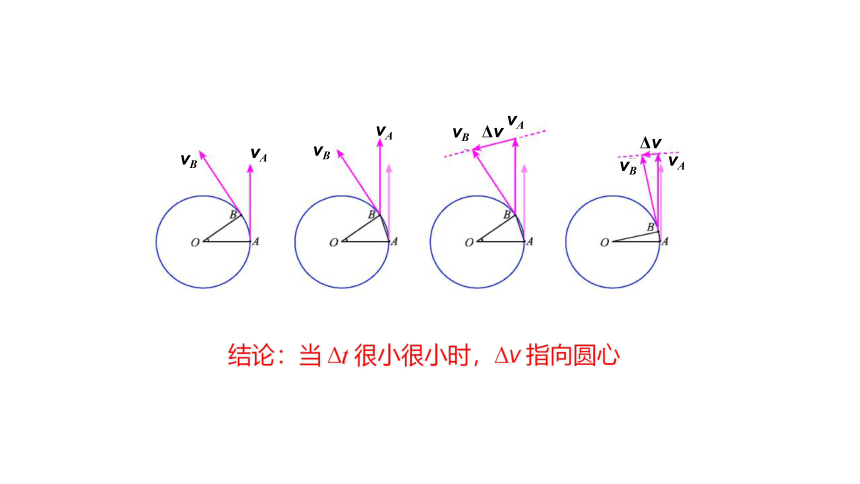
结论:当 Δt 很小很小时,Δv 指向圆心
vA
vB
vA
vB
vA
vB
Δv
vA
vB
Δv
新课入
O
B
A
v
v
v
Δv
Δθ
Δθ
新课入
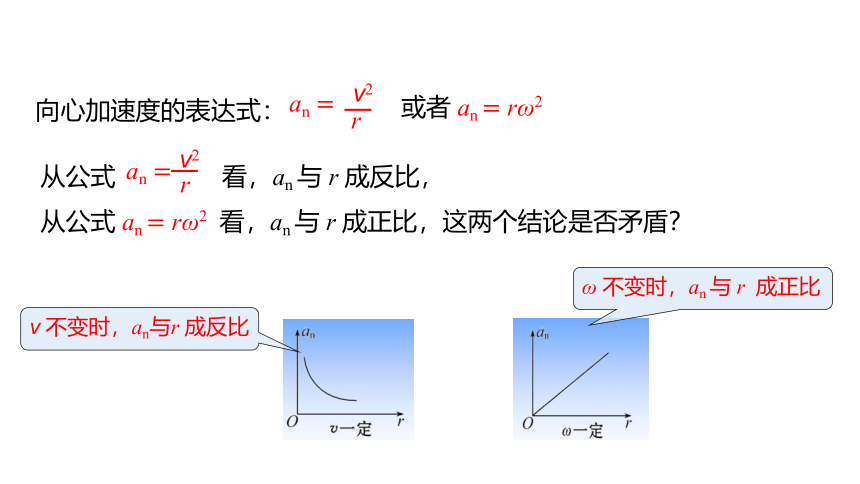
向心加速度的表达式:
v 不变时,an与r 成反比
ω 不变时,an 与 r 成正比
an
v2
r
或者 an rω2
从公式 看,an 与 r 成反比,
从公式 an rω2 看,an 与 r 成正比,这两个结论是否矛盾?
an
v2
r
1.定义:匀速圆周运动的加速度
2.意义:描述速度方向变化的快慢
3.大小:
4.方向:始终指向圆心(时刻改变)
匀速圆周运动是变加速运动
向心加速度
an
v2
r
或者 an rω2
新课入
小结
例1 .关于北京和广州随地球自转的向心加速度,下列说法中正确的是( )
A .它们的方向都沿半径指向地心
B. 它们的方向都平行于赤道平面指向地轴
C .北京的向心加速度比广州的向心加速度大
D .北京的向心加速度比广州的向心加速度小
新课入
例2 如图4所示,一球体绕轴O1O2以角速度ω匀速旋转,A、B为球体表面上两点,下列说法正确的是( )
A.A、B两点具有相同的角速度
B.A、B两点具有相同的线速度
C.A、B两点的向心加速度的方向都指向球心
D.A、B两点的向心加速度大小之比为2∶1
√
图4
新课入
A
3. 如图所示,为A、B两质点做匀速圆周运动的向心加速度随半径变化的图像,其中A为双曲线的一个分支,由图可知 ( )
A.A 物体运动的线速度大小不变
B.A 物体运动的角速度大小不变
C.B 物体运动的角速度大小不变
D.B 物体运动的线速度大小不变
AC
自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点 A、B、C,如图 所示。其中哪两点向心加速度的关系适用于“向心加速度与半径成正比”,哪两点适用于“向心加速度与半径成反比”?给出解释。
例4 (多选)如图所示,皮带传动装置中,右边两轮连在一起共轴转动,图中三轮半径分别为r1=3r,r2=2r,r3=4r;A、B、C三点为三个轮边缘上的点,向心加速度大小分别为a1、a2、a3,皮带不打滑,则下列比例关系正确的是( )
新课入
BD
例5 在长为L的细绳下端拴一个质量为m的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就绕圆锥面旋转,这样就成了一个圆锥摆。细绳与竖直方向成 θ 角,求小球做匀速圆周运动的向心加速度大小为多少?通过计算说明:要增大夹角θ,应该增大小球运动的角速度ω。
O′
O
mg
FT
F
θ
L
R
O′
O
mg
FT
F
θ
L
小球做圆周运动的半径 R = Lsin θ ②
R
解:小球的向心力由 FT 和 G 的合力提供
Fn = F = mgtan θ
m
an
Fn
①
把向心加速度公式的半径 an R ω2和②代入①式,可得
θ
lω2
新课入
O1
O2
6.暑假里,小明和同学去赭山游乐场游玩,坐了一次名叫“摇头飞椅”的游艺机,如图a所示,该游艺机顶上有一个半径为4.5m的“伞盖”,“伞盖”在转动过程中带动下面的悬绳转动,其示意图如图b所示。“摇头飞椅”高O1O2=5.8m,绳长5m。小明挑选了一个悬挂在“伞盖”边缘的最外侧的椅子坐下,他与座椅的总质量为40kg。小明和椅子的转动可简化为如图b所示的圆周运动。在某段时间内,“伞盖”保持在水平面内稳定旋转,绳与竖直方向夹角为37 。g取10m/s2,sin37 =0.6, cos37 =0.8,在此过程中,求: 游艺机转动的角速度大小;
2圆锥形的物体受的向心力
例5 如图所示,竖直固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面内做匀速圆周运动.以下关于A、B两球做圆周运动时的线速度(vA、vB)、角速度(ωA、ωB)、加速度(aA、aB)和对内壁的压力(FNA、FNB)的关系式正确的是( )
A.vA>vB B.ωA>ωB
C.aA>aB D.FNA>FNB
新课入
C
加速度的大小怎么计算呢
在同一条直线上
v1
v2
Δv =?
v1
v2
Δv =?
v1
v2
Δv =?
不在同一条直线上
Δv = v2 v1
新课入
设质点沿半径为 r 的圆做匀速圆周运动,某时刻位于 A 点,速度为 vA ,经过时间 Δt 后位于 B 点,速度为 vB 。
Δv
O
A
B
vB
vA
Δv
B
vB
vA
Δv
B
vB
vA
vA
Δv
vB
vA
A
O
Δv 逐渐趋向于平行 OA
新课入
结论:当 Δt 很小很小时,Δv 指向圆心
vA
vB
vA
vB
vA
vB
Δv
vA
vB
Δv
新课入
O
B
A
v
v
v
Δv
Δθ
Δθ
新课入
向心加速度的表达式:
v 不变时,an与r 成反比
ω 不变时,an 与 r 成正比
an
v2
r
或者 an rω2
从公式 看,an 与 r 成反比,
从公式 an rω2 看,an 与 r 成正比,这两个结论是否矛盾?
an
v2
r
1.定义:匀速圆周运动的加速度
2.意义:描述速度方向变化的快慢
3.大小:
4.方向:始终指向圆心(时刻改变)
匀速圆周运动是变加速运动
向心加速度
an
v2
r
或者 an rω2
新课入
小结
例1 .关于北京和广州随地球自转的向心加速度,下列说法中正确的是( )
A .它们的方向都沿半径指向地心
B. 它们的方向都平行于赤道平面指向地轴
C .北京的向心加速度比广州的向心加速度大
D .北京的向心加速度比广州的向心加速度小
新课入
例2 如图4所示,一球体绕轴O1O2以角速度ω匀速旋转,A、B为球体表面上两点,下列说法正确的是( )
A.A、B两点具有相同的角速度
B.A、B两点具有相同的线速度
C.A、B两点的向心加速度的方向都指向球心
D.A、B两点的向心加速度大小之比为2∶1
√
图4
新课入
A
3. 如图所示,为A、B两质点做匀速圆周运动的向心加速度随半径变化的图像,其中A为双曲线的一个分支,由图可知 ( )
A.A 物体运动的线速度大小不变
B.A 物体运动的角速度大小不变
C.B 物体运动的角速度大小不变
D.B 物体运动的线速度大小不变
AC
自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点 A、B、C,如图 所示。其中哪两点向心加速度的关系适用于“向心加速度与半径成正比”,哪两点适用于“向心加速度与半径成反比”?给出解释。
例4 (多选)如图所示,皮带传动装置中,右边两轮连在一起共轴转动,图中三轮半径分别为r1=3r,r2=2r,r3=4r;A、B、C三点为三个轮边缘上的点,向心加速度大小分别为a1、a2、a3,皮带不打滑,则下列比例关系正确的是( )
新课入
BD
例5 在长为L的细绳下端拴一个质量为m的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就绕圆锥面旋转,这样就成了一个圆锥摆。细绳与竖直方向成 θ 角,求小球做匀速圆周运动的向心加速度大小为多少?通过计算说明:要增大夹角θ,应该增大小球运动的角速度ω。
O′
O
mg
FT
F
θ
L
R
O′
O
mg
FT
F
θ
L
小球做圆周运动的半径 R = Lsin θ ②
R
解:小球的向心力由 FT 和 G 的合力提供
Fn = F = mgtan θ
m
an
Fn
①
把向心加速度公式的半径 an R ω2和②代入①式,可得
θ
lω2
新课入
O1
O2
6.暑假里,小明和同学去赭山游乐场游玩,坐了一次名叫“摇头飞椅”的游艺机,如图a所示,该游艺机顶上有一个半径为4.5m的“伞盖”,“伞盖”在转动过程中带动下面的悬绳转动,其示意图如图b所示。“摇头飞椅”高O1O2=5.8m,绳长5m。小明挑选了一个悬挂在“伞盖”边缘的最外侧的椅子坐下,他与座椅的总质量为40kg。小明和椅子的转动可简化为如图b所示的圆周运动。在某段时间内,“伞盖”保持在水平面内稳定旋转,绳与竖直方向夹角为37 。g取10m/s2,sin37 =0.6, cos37 =0.8,在此过程中,求: 游艺机转动的角速度大小;
2圆锥形的物体受的向心力
例5 如图所示,竖直固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面内做匀速圆周运动.以下关于A、B两球做圆周运动时的线速度(vA、vB)、角速度(ωA、ωB)、加速度(aA、aB)和对内壁的压力(FNA、FNB)的关系式正确的是( )
A.vA>vB B.ωA>ωB
C.aA>aB D.FNA>FNB
新课入
C
