2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 313.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 21:21:22 | ||
图片预览



文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 将一个圆形纸板放在太阳光下,它在地面上所形成的影子的形状不可能是( )
A.圆 B.三角形
C.线段 D.椭圆
2. 如果在同一时刻的阳光下,小莉的影子比小玉的影子长,那么在同一路灯下( )
A.小莉的影子比小玉的影子长
B.小莉的影子比小玉的影子短
C.小莉的影子与小玉的影子一样长
D.无法判断谁的影子长
3. 如图是某几何体的三视图,该几何体是( )
A.圆柱 B.三棱柱
C.四棱柱 D.四棱锥
4. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
5. 一个几何体的三视图如图所示,网格中小正方形的边长均为1,那么下列选项中最接近这个几何体的侧面积的是( )
A. 24.0 B. 62.8
C. 74.2 D. 113.0
6. 如图所示正三棱柱的主视图是( )
A B C D
7. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
A.仅主视图不同
B.仅俯视图不同
C.仅左视图不同
D.主视图、左视图和俯视图都相同
8. 下列立体图形中,俯视图是正方形的是( )
A B C D
9.要制作一个密封的长方体铁盒,嘉嘉设计出了它的三视图如图所示,按图中尺寸(单位:cm)判断,要制作这个长方体铁盒,如果只考虑面积因素,采用下列哪种面积的铁板最合理( )
A.1 000 cm2 B.1 030 cm2
C.1 100 cm2 D.1 200 cm2
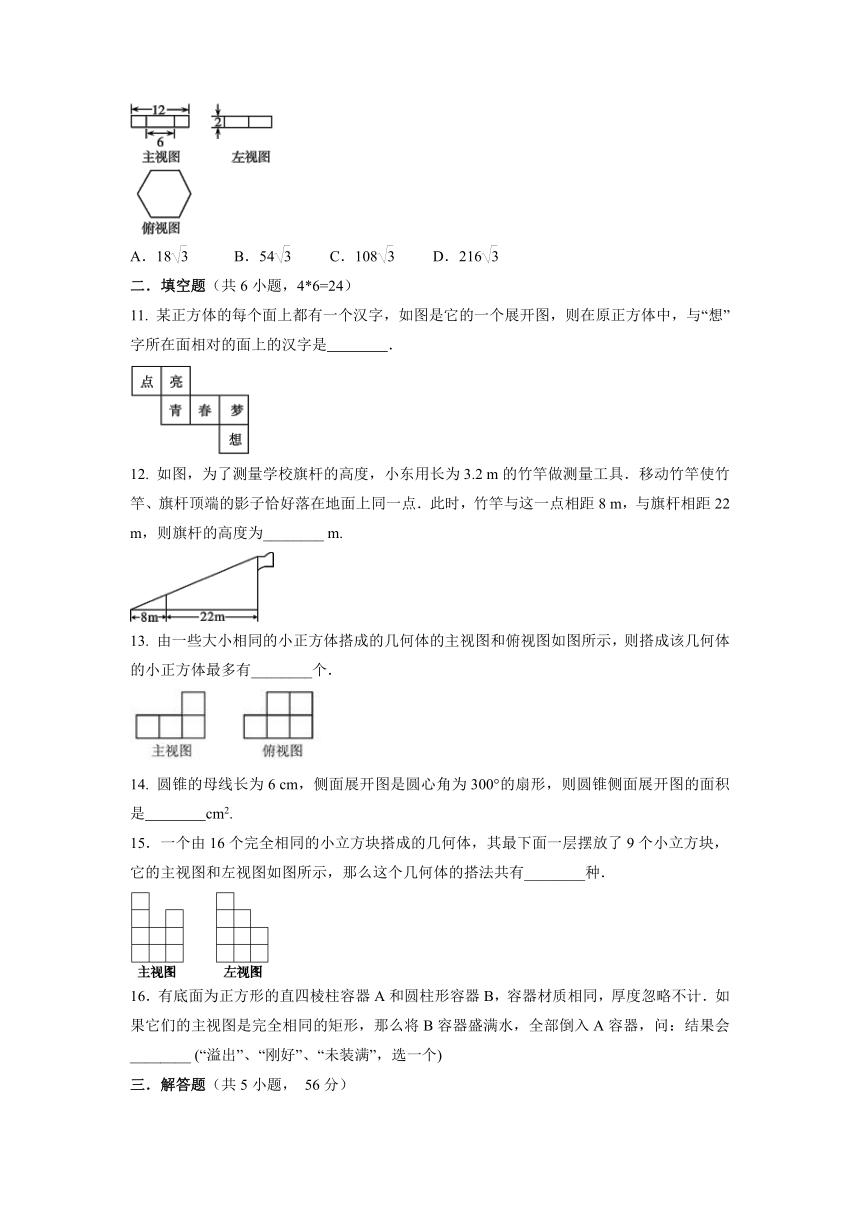
10. 如图所示的是某几何体的三视图,则该几何体的体积是( )
A.18 B.54 C.108 D.216
二.填空题(共6小题,4*6=24)
11. 某正方体的每个面上都有一个汉字,如图是它的一个展开图,则在原正方体中,与“想”字所在面相对的面上的汉字是 .
12. 如图,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面上同一点.此时,竹竿与这一点相距8 m,与旗杆相距22 m,则旗杆的高度为________ m.
13. 由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示,则搭成该几何体的小正方体最多有________个.
14. 圆锥的母线长为6 cm,侧面展开图是圆心角为300°的扇形,则圆锥侧面展开图的面积是 cm2.
15.一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有________种.
16.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,问:结果会________ (“溢出”、“刚好”、“未装满”,选一个)
三.解答题(共5小题, 56分)
17.(6分) 如图是两根标杆AC,BD及它们在灯光下的影子,请在图中画出光源的位置(用点P表示),并在图中画出人在此光源下的影子(用线段EF表示).
18.(8分) 有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6,甲、乙、丙三位同学从三个不同的角度去观察此正方体,观察结果如图所示,请画出正方体的一种表面展开图,(要求把数字标注在表面展开图中)
19.(8分) 如图,已知线段AB=2 cm,投影面为P,太阳光线与投影面垂直.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图②),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图③中画出线段AB的正投影,并求出其正投影的长.
20.(10分) 已知某几何体的三视图如图所示,其中俯视图为正六边形,求该几何体的表面积.
21.(12分) 如图,公路旁有两个高度相等的路灯AB,CD.数学老师杨柳上午去学校时发现高1米的木棒的影子为5米,此时路灯AB在太阳光下的影子恰好落在里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习后回家时,站在上午同一个地方,杨老师发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
(1)在图中画出杨老师的位置,并画出光线,标明太阳光、灯光;
(2)若杨老师身高为1.8米,他离里程碑E恰4米,求路灯的高.
22.(12分) 为加快新农村建设,某市投入资金建设新型农村社区.如图为住宅区内的两幢楼,它们的高AB=CD=30 m,现需了解甲楼对乙楼采光情况的影响.当太阳光线与水平线的夹角为30°时,试求:
(1)若两楼间的距离AC=24 m,则甲楼的影子落在乙楼上有多高.(结果保留根号)
(2)若甲楼的影子刚好不影响乙楼,则两楼之间的距离应当有多远.(结果保留根号)
参考答案
1-5 BDCBB 6-10BDBCC
11.亮
12.12
13.7
14. 30π
15.10
16. 未装满
17. 解:连接A′C,B′D并延长,交点P即为光源的位置;连接点P与人的头顶并延长,交过点E的水平线于点F,则EF即为人在此光源下的影子,画图略.
18. 解:从3个小立方体上的数可知,与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5面,同理,立方体面上数字3对6.故立方体面上数字2对4.作图为:
19. 解:(1)如图①,点C即为所求.
(2)如图②,线段CD即为所求,正投影的长为2 cm.
(3)如图③,线段CD即为所求,正投影的长为2cos30°= cm.
20. 解:观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为2,高为4,∴正六边形的外接圆半径为2,∴正六边形的中心到边的距离==.几何体的侧面积=2×4×6=48.上下底面积之和=2××6×2×=12 ,∴几何体的表面积=侧面积+ 底面积=48+12 .答:该几何体的表面积为48+12 .
21. 解:(1)如图所示,GF表示杨老师的位置.
(2)∵上午去学校时,高1米的木棒的影子为5米,杨老师身高为1.8米,∴杨老师的影长CF为5×1.8=9(米),∵GF⊥AC,DC⊥AC,∴GF∥CD,∴△EGF∽△EDC,∴=,∴=,解得CD=5.85.故路灯高5.85米.
22.解:(1)∵AB=CD=30 m,BA⊥AC,CD⊥AC,∴四边形ABDC是矩形.∴BD=AC=24 m,∠BDE=90°.∵∠DBE=30°,∴设DE=x m,则BE=2x m.∴在Rt△BDE中,BD===x(m).∴x=24,解得x=8.∴EC=CD-DE=(30-8)m,即甲楼的影子落在乙楼上有(30-8)m高.
(2)如图.当太阳光照射到点C时,甲楼的影子刚好不影响乙楼,在Rt△ABC中,AB=30 m,∠ACB=30°,∴BC=2AB=60 m.在Rt△ABC中,由勾股定理得AC===30(m).∴若甲楼的影子刚好不影响乙楼,则两楼之间的距离应当为30 m.
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 将一个圆形纸板放在太阳光下,它在地面上所形成的影子的形状不可能是( )
A.圆 B.三角形
C.线段 D.椭圆
2. 如果在同一时刻的阳光下,小莉的影子比小玉的影子长,那么在同一路灯下( )
A.小莉的影子比小玉的影子长
B.小莉的影子比小玉的影子短
C.小莉的影子与小玉的影子一样长
D.无法判断谁的影子长
3. 如图是某几何体的三视图,该几何体是( )
A.圆柱 B.三棱柱
C.四棱柱 D.四棱锥
4. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
5. 一个几何体的三视图如图所示,网格中小正方形的边长均为1,那么下列选项中最接近这个几何体的侧面积的是( )
A. 24.0 B. 62.8
C. 74.2 D. 113.0
6. 如图所示正三棱柱的主视图是( )
A B C D
7. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
A.仅主视图不同
B.仅俯视图不同
C.仅左视图不同
D.主视图、左视图和俯视图都相同
8. 下列立体图形中,俯视图是正方形的是( )
A B C D
9.要制作一个密封的长方体铁盒,嘉嘉设计出了它的三视图如图所示,按图中尺寸(单位:cm)判断,要制作这个长方体铁盒,如果只考虑面积因素,采用下列哪种面积的铁板最合理( )
A.1 000 cm2 B.1 030 cm2
C.1 100 cm2 D.1 200 cm2
10. 如图所示的是某几何体的三视图,则该几何体的体积是( )
A.18 B.54 C.108 D.216
二.填空题(共6小题,4*6=24)
11. 某正方体的每个面上都有一个汉字,如图是它的一个展开图,则在原正方体中,与“想”字所在面相对的面上的汉字是 .
12. 如图,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面上同一点.此时,竹竿与这一点相距8 m,与旗杆相距22 m,则旗杆的高度为________ m.
13. 由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示,则搭成该几何体的小正方体最多有________个.
14. 圆锥的母线长为6 cm,侧面展开图是圆心角为300°的扇形,则圆锥侧面展开图的面积是 cm2.
15.一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有________种.
16.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,问:结果会________ (“溢出”、“刚好”、“未装满”,选一个)
三.解答题(共5小题, 56分)
17.(6分) 如图是两根标杆AC,BD及它们在灯光下的影子,请在图中画出光源的位置(用点P表示),并在图中画出人在此光源下的影子(用线段EF表示).
18.(8分) 有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6,甲、乙、丙三位同学从三个不同的角度去观察此正方体,观察结果如图所示,请画出正方体的一种表面展开图,(要求把数字标注在表面展开图中)
19.(8分) 如图,已知线段AB=2 cm,投影面为P,太阳光线与投影面垂直.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图②),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图③中画出线段AB的正投影,并求出其正投影的长.
20.(10分) 已知某几何体的三视图如图所示,其中俯视图为正六边形,求该几何体的表面积.
21.(12分) 如图,公路旁有两个高度相等的路灯AB,CD.数学老师杨柳上午去学校时发现高1米的木棒的影子为5米,此时路灯AB在太阳光下的影子恰好落在里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习后回家时,站在上午同一个地方,杨老师发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
(1)在图中画出杨老师的位置,并画出光线,标明太阳光、灯光;
(2)若杨老师身高为1.8米,他离里程碑E恰4米,求路灯的高.
22.(12分) 为加快新农村建设,某市投入资金建设新型农村社区.如图为住宅区内的两幢楼,它们的高AB=CD=30 m,现需了解甲楼对乙楼采光情况的影响.当太阳光线与水平线的夹角为30°时,试求:
(1)若两楼间的距离AC=24 m,则甲楼的影子落在乙楼上有多高.(结果保留根号)
(2)若甲楼的影子刚好不影响乙楼,则两楼之间的距离应当有多远.(结果保留根号)
参考答案
1-5 BDCBB 6-10BDBCC
11.亮
12.12
13.7
14. 30π
15.10
16. 未装满
17. 解:连接A′C,B′D并延长,交点P即为光源的位置;连接点P与人的头顶并延长,交过点E的水平线于点F,则EF即为人在此光源下的影子,画图略.
18. 解:从3个小立方体上的数可知,与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5面,同理,立方体面上数字3对6.故立方体面上数字2对4.作图为:
19. 解:(1)如图①,点C即为所求.
(2)如图②,线段CD即为所求,正投影的长为2 cm.
(3)如图③,线段CD即为所求,正投影的长为2cos30°= cm.
20. 解:观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为2,高为4,∴正六边形的外接圆半径为2,∴正六边形的中心到边的距离==.几何体的侧面积=2×4×6=48.上下底面积之和=2××6×2×=12 ,∴几何体的表面积=侧面积+ 底面积=48+12 .答:该几何体的表面积为48+12 .
21. 解:(1)如图所示,GF表示杨老师的位置.
(2)∵上午去学校时,高1米的木棒的影子为5米,杨老师身高为1.8米,∴杨老师的影长CF为5×1.8=9(米),∵GF⊥AC,DC⊥AC,∴GF∥CD,∴△EGF∽△EDC,∴=,∴=,解得CD=5.85.故路灯高5.85米.
22.解:(1)∵AB=CD=30 m,BA⊥AC,CD⊥AC,∴四边形ABDC是矩形.∴BD=AC=24 m,∠BDE=90°.∵∠DBE=30°,∴设DE=x m,则BE=2x m.∴在Rt△BDE中,BD===x(m).∴x=24,解得x=8.∴EC=CD-DE=(30-8)m,即甲楼的影子落在乙楼上有(30-8)m高.
(2)如图.当太阳光照射到点C时,甲楼的影子刚好不影响乙楼,在Rt△ABC中,AB=30 m,∠ACB=30°,∴BC=2AB=60 m.在Rt△ABC中,由勾股定理得AC===30(m).∴若甲楼的影子刚好不影响乙楼,则两楼之间的距离应当为30 m.
