人教版五年级数学下册 3.8 体积单位间的进率 上课课件(共57张PPT)
文档属性
| 名称 | 人教版五年级数学下册 3.8 体积单位间的进率 上课课件(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 15:18:55 | ||
图片预览








文档简介
(共57张PPT)
第8课时 体积单位间的进率
长方体和正方体
3
人教版五年级数学下册 上课课件
学习目标
1. 让学生通过观察、操作、实验, 体会并理解体积的含义, 认识常用的体积单位: 立方米、立方分米、立方厘米
2. 让学生初步建立空间大小的概念, 知道体积的含义, 发展学生的空间观念。初步掌握计量物体体积的单位, 能选择恰当的体积单位估算常见物体的体积。
3. 培养学生的观察能力、实践能力以及合作学习的能力, 扩展学生的思维,进一步发展学生的空间观念。
学习重点 难点
【教学重点】
感知物体的体积, 初步建立1 立方米、1 立方分米、1 立方厘米的体积观念。
【教学难点】
能正确应用体积单位估算常见物体的体积。
乌鸦是怎样喝到水的 为什么
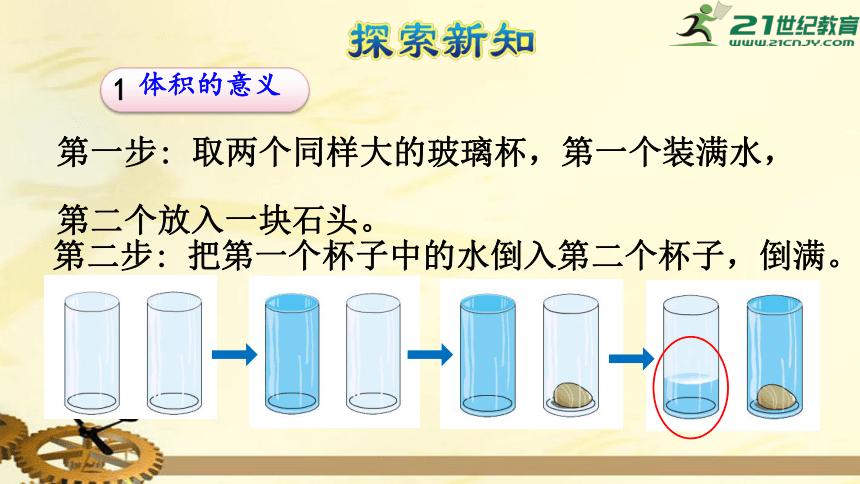
第一步: 取两个同样大的玻璃杯,第一个装满水,
第二个放入一块石头。
第二步: 把第一个杯子中的水倒入第二个杯子,倒满。
体积的意义
1
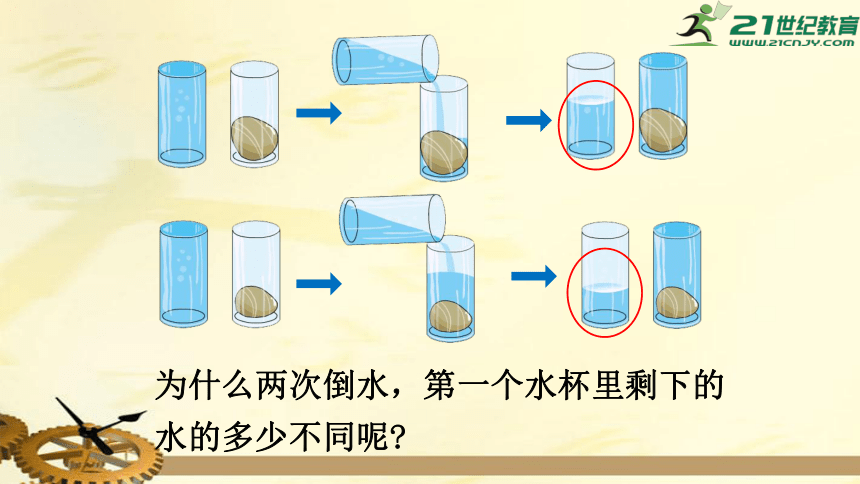
为什么两次倒水,第一个水杯里剩下的水的多少不同呢
物体所占的空间有大有小。
下面的洗衣机、影碟机和手机,哪个所占空间大?
物体所占空间的大小叫做物体的体积。
洗衣机的体积最大,手机的体积最小。
比较两个物体体积的大小,要用统一的体积单位来测量。
常用的体积单位
2
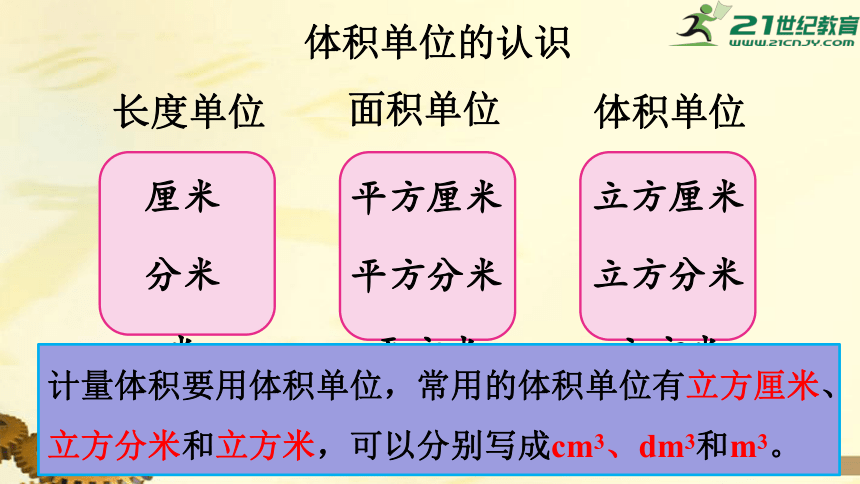
体积单位的认识
长度单位
面积单位
体积单位
厘米
分米
米
平方厘米
平方分米
平方米
立方厘米
立方分米
立方米
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3和m3。
1.口算。
⑴ 一个长方体,它的底面积是30 dm ,
高是6dm, 这个长方体的体积是多少?
30×6 = 180 (dm )
答:这个长方体的体积是180立方分米。
1.口算。
⑵ 一个正方体,横截面的面积是25cm ,
棱长是5cm,这个正方体的体积是多少?
25×5 = 125 (cm )
答:这个正方体的体积是125立方厘米。
1.口算。
⑶ 一个长方体底面积是12 cm ,体积是
48 cm ,这个长方体的高是多少?
48÷12 = 4 (cm)
答:这个长方体的高是4厘米。
2.我们平时在测量物体时:
(1)常用的长度单位有哪些?
米 分米 厘米
2.我们平时在测量物体时:
(2)常用的面积单位有哪些?
平方米 平方分米 平方厘米
2.我们平时在测量物体时:
(3)常用的体积单位有哪些?
立方米 立方分米 立方厘米
3.填一填。
(1)棱长是1cm的正方体,体积是( )。
(2)棱长是1dm的正方体,体积是( )。
(3)棱长是( )的正方体,体积是1m3。
1dm3
1m
1cm3
下图是一个棱长为1dm的正方体,体积是1dm。想一想,它的体积是多少立方厘米呢?
2
如果把它的棱长看作是10cm,可以把它切成1000块1cm 的小正方体。
它的底面积是1dm ,就100cm ,100×10,一共是1000cm 。
。
上
课件PPT
10×10×10=1000(cm )
1dm =1000 cm
上
课件PPT
1dm3=______cm3
1000
1m3=______dm3
1000
仿照上面的方法,你能推算出 1m3等于多少立方分米吗
上
课件PPT
单位名称 相邻两个单位间的进率
长度 米、分米、厘米
面积 平方米、平方分米、平方厘米
体积 立方米、立方分米、立方厘米
10
100
1000
到现在为止,我们已经学习了哪些计量单位?请整理在表中。
(1)3.8m3是多少立方分米
想: 1m3= dm3
3.8m3= dm3
自己试一试!
1000
3800
3
(2)2400cm3是多少立方分米
想: cm3= 1dm3
2400cm3= dm3
自己试一试!
1000
2.4
3
这个牛奶包装箱的体积是多少
箱上的尺寸一般是这个长方体的长、宽、高。
50cm
30cm
40cm
4
这个牛奶包装箱的体积是多少
50cm
30cm
40cm
=50×30×40
=60000(cm3)
60000cm3=60dm3=0.06m3
V=a b h
答:这个牛奶包装箱的体积是0.06m3 。
4
上
课件PPT
1. 3.5dm3= cm3
想: 1dm3= cm3
3.5dm3= cm3
1000
3500
3500
上
课件PPT
1. 700dm3= m3
0.7
想: dm3= 1m3
700dm3= m3
1000
0.7
上
课件PPT
1. 0.25m3= cm3
250000
想: 1m3= dm3 = cm3
0.25m3= cm3
1000
250000
1000000
上
课件PPT
2.要砌一道长15m、厚24cm、高3m的砖墙。如果每立方米用砖525块,一共要用砖多少块?
计算前先要注意什么?
要先统一单位。
上
课件PPT
2.要砌一道长15m、厚24cm、高3m的砖墙。如果每立方米用砖525块,一共要用砖多少块?
24cm=0.24m
V =a b h
=15×0.24×3 =10.8(m3)
10.8×525=5670(块)
答:一共要用砖5670块。
1.相邻体积单位之间的进率是1000,即1m3=1000dm3,1dm3=1000cm3
2.把高级单位转化为低级单位时,乘进率;把低级单位转化成高级单位时,除以进率。
教材P36T1
1. 1.02m3= dm3 960dm3= m3
6270cm3= dm3 23dm3= cm3
36000cm3= dm3 8.63m2= dm2
1020
0.96
6.27
23000
36
863
教材P36T2
2.一个长方体包装盒,从里面量长28cm,宽20cm,体积为11.76dm3。爸爸想用它包装一件长25cm,宽16cm,高18cm的玻璃器皿,是否可以装得下?
想一想,能装下吗?
教材P36T2
2.一个长方体包装盒,从里面量长28cm,宽20cm,里面的体积为11.76dm3。爸爸想用它包装一件长25cm、宽16cm、高18cm的玻璃器皿,是否可以装得下?
11.76 dm3=11760 cm3
11760÷(28×20)=21(cm)
21>18
答:可以装下。
教材P36T3
3.花园小区为居民新安装了50个休息的凳子,凳面的长、宽、高分别是100cm、45cm、4.5cm,凳腿的长、宽、高分别是45cm、5cm、35cm。做这些凳子至少用了混凝土多少方?
教材P36T3
3.花园小区为居民新安装了50个休息的凳子,凳面的长、宽、高分别是100cm、45cm、4.5cm,凳腿的长、宽、高分别是45cm、5cm、35cm。做这些凳子至少用了混凝土多少方?
(100×45×4.5+45×5×35×2)×50
=1800000(cm3)=1.8(m3)=1.8(方)
答:做这些凳子至少用了混凝土1.8方。
教材P36T4
4.“六一”儿童节前,全市的小学生代表用棱长3cm的正方体塑料拼插积木在广场中央搭起了一面长6m、高2.7m、厚6cm的奥运心愿墙,这面墙一共用了多少块积木?
教材P36T4
4.“六一”儿童节前,全市的小学生代表用棱长3cm的正方体塑料拼插积木在广场中央搭起了一面长6m、高2.7m、厚6cm的奥运心愿墙,这面墙一共用了多少块积木?
6 m=600 cm 2.7 m=270 cm
600×270×6÷(3×3×3)=36000(块)
答:这面墙一共用了36000块积木。
教材P36T5
5.学校运来7.6m 的沙子,铺在一个长5m、宽38dm的沙坑里,可以铺多厚?
h=V÷a÷b
根据V=abh,有:
=7.6÷5÷3.8
=0.4(米)
38分米=3.8米
答:可以铺0.4米厚。
教材P36T6
6.请你圈出每组数据中与其他数据不相等的那个数。
(1)5.08 m3 50800 cm3
5080 dm3 5080000 cm3
教材P36T6翼
6.请你圈出每组数据中与其他数据不相等的那个数。
(2)6039dm2 6.039m2
603900cm2 60.39m2
教材P36T6
6.请你圈出每组数据中与其他数据不相等的那个数。
(3)1500cm 1500dm
15m 150dm
教材P37T7
7.一个长方体的无盖水族箱,长是6m,宽是60cm,高是1.5m。这个水族箱占地面积有多大?需要用多少平方米的玻璃?它的体积是多少?
教材P37T7
7.一个长方体的无盖水族箱,长是6m,宽是60cm,高是1.5m。这个水族箱占地面积有多大?需要用多少平方米的玻璃?它的体积是多少?
占地面积:
60厘米=0.6米
6×0.6=3.6(平方米)
答:这个水族箱占地3.6平方米。
教材P37T7
7.一个长方体的无盖水族箱,长是6m,宽是60cm,高是1.5m。这个水族箱占地面积有多大?需要用多少平方米的玻璃?它的体积是多少?
玻璃:
6×0.6+6×1.5×2+1.5×0.6×2
=3.6+18+1.8
=23.4(平方米)
答:这个水族箱需要23.4平方米的玻璃。
教材P37T7
7.一个长方体的无盖水族箱,长是6m,宽是60cm,高是1.5m。这个水族箱占地面积有多大?需要用多少平方米的玻璃?它的体积是多少?
体积:V=abh
答:这个水族箱的体积是5.4立方米。
=6×0.6×1.5
=5.4(立方米)
教材P37T9
1.茶厂工人将长、宽各为20cm,高为10cm的长方体茶盒装入棱长为30cm的正方体纸箱,最多能装几盒?怎样才能装下?
教材P37T9
求能装几盒,用纸箱体积除以茶盒体积就行了。
教材P37T9
这样做,行吗?
30 ×30 ×30 ÷(20 ×20 ×10)
=27000 ÷4000
=6.75(个)
≈6(个)
教材P37T9
这样做不行!这不符合实际情况。
教材P37T9
最多能装5盒。其中3盒摞在一起,靠一个角码放,另外2个竖起,放在空余位置。
教材P37T9
求最多能装几盒,不能直接用纸箱体积除以茶盒体积,要根据实际情况进行分析。由于茶盒高10厘米,而纸箱棱长为30厘米,所以先考虑用3个茶盒摞起来,这样充分利用空间。纸箱所剩空间不能完全利用,长、宽各剩10厘米,只能考虑让茶盒竖起码放,只能再放2个。所以最多能装5盒。
把棱长为1m的正方体切割成棱长是1㎝的小正方体,把这些小正方体一个挨一个地连起来,可以排多长?
1m = 1000000 cm ,
1000000个小正方体一个挨一个地连起来,可以排1000000cm,
1000000cm =10000m =10km。
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第8课时 体积单位间的进率
长方体和正方体
3
人教版五年级数学下册 上课课件
学习目标
1. 让学生通过观察、操作、实验, 体会并理解体积的含义, 认识常用的体积单位: 立方米、立方分米、立方厘米
2. 让学生初步建立空间大小的概念, 知道体积的含义, 发展学生的空间观念。初步掌握计量物体体积的单位, 能选择恰当的体积单位估算常见物体的体积。
3. 培养学生的观察能力、实践能力以及合作学习的能力, 扩展学生的思维,进一步发展学生的空间观念。
学习重点 难点
【教学重点】
感知物体的体积, 初步建立1 立方米、1 立方分米、1 立方厘米的体积观念。
【教学难点】
能正确应用体积单位估算常见物体的体积。
乌鸦是怎样喝到水的 为什么
第一步: 取两个同样大的玻璃杯,第一个装满水,
第二个放入一块石头。
第二步: 把第一个杯子中的水倒入第二个杯子,倒满。
体积的意义
1
为什么两次倒水,第一个水杯里剩下的水的多少不同呢
物体所占的空间有大有小。
下面的洗衣机、影碟机和手机,哪个所占空间大?
物体所占空间的大小叫做物体的体积。
洗衣机的体积最大,手机的体积最小。
比较两个物体体积的大小,要用统一的体积单位来测量。
常用的体积单位
2
体积单位的认识
长度单位
面积单位
体积单位
厘米
分米
米
平方厘米
平方分米
平方米
立方厘米
立方分米
立方米
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3和m3。
1.口算。
⑴ 一个长方体,它的底面积是30 dm ,
高是6dm, 这个长方体的体积是多少?
30×6 = 180 (dm )
答:这个长方体的体积是180立方分米。
1.口算。
⑵ 一个正方体,横截面的面积是25cm ,
棱长是5cm,这个正方体的体积是多少?
25×5 = 125 (cm )
答:这个正方体的体积是125立方厘米。
1.口算。
⑶ 一个长方体底面积是12 cm ,体积是
48 cm ,这个长方体的高是多少?
48÷12 = 4 (cm)
答:这个长方体的高是4厘米。
2.我们平时在测量物体时:
(1)常用的长度单位有哪些?
米 分米 厘米
2.我们平时在测量物体时:
(2)常用的面积单位有哪些?
平方米 平方分米 平方厘米
2.我们平时在测量物体时:
(3)常用的体积单位有哪些?
立方米 立方分米 立方厘米
3.填一填。
(1)棱长是1cm的正方体,体积是( )。
(2)棱长是1dm的正方体,体积是( )。
(3)棱长是( )的正方体,体积是1m3。
1dm3
1m
1cm3
下图是一个棱长为1dm的正方体,体积是1dm。想一想,它的体积是多少立方厘米呢?
2
如果把它的棱长看作是10cm,可以把它切成1000块1cm 的小正方体。
它的底面积是1dm ,就100cm ,100×10,一共是1000cm 。
。
上
课件PPT
10×10×10=1000(cm )
1dm =1000 cm
上
课件PPT
1dm3=______cm3
1000
1m3=______dm3
1000
仿照上面的方法,你能推算出 1m3等于多少立方分米吗
上
课件PPT
单位名称 相邻两个单位间的进率
长度 米、分米、厘米
面积 平方米、平方分米、平方厘米
体积 立方米、立方分米、立方厘米
10
100
1000
到现在为止,我们已经学习了哪些计量单位?请整理在表中。
(1)3.8m3是多少立方分米
想: 1m3= dm3
3.8m3= dm3
自己试一试!
1000
3800
3
(2)2400cm3是多少立方分米
想: cm3= 1dm3
2400cm3= dm3
自己试一试!
1000
2.4
3
这个牛奶包装箱的体积是多少
箱上的尺寸一般是这个长方体的长、宽、高。
50cm
30cm
40cm
4
这个牛奶包装箱的体积是多少
50cm
30cm
40cm
=50×30×40
=60000(cm3)
60000cm3=60dm3=0.06m3
V=a b h
答:这个牛奶包装箱的体积是0.06m3 。
4
上
课件PPT
1. 3.5dm3= cm3
想: 1dm3= cm3
3.5dm3= cm3
1000
3500
3500
上
课件PPT
1. 700dm3= m3
0.7
想: dm3= 1m3
700dm3= m3
1000
0.7
上
课件PPT
1. 0.25m3= cm3
250000
想: 1m3= dm3 = cm3
0.25m3= cm3
1000
250000
1000000
上
课件PPT
2.要砌一道长15m、厚24cm、高3m的砖墙。如果每立方米用砖525块,一共要用砖多少块?
计算前先要注意什么?
要先统一单位。
上
课件PPT
2.要砌一道长15m、厚24cm、高3m的砖墙。如果每立方米用砖525块,一共要用砖多少块?
24cm=0.24m
V =a b h
=15×0.24×3 =10.8(m3)
10.8×525=5670(块)
答:一共要用砖5670块。
1.相邻体积单位之间的进率是1000,即1m3=1000dm3,1dm3=1000cm3
2.把高级单位转化为低级单位时,乘进率;把低级单位转化成高级单位时,除以进率。
教材P36T1
1. 1.02m3= dm3 960dm3= m3
6270cm3= dm3 23dm3= cm3
36000cm3= dm3 8.63m2= dm2
1020
0.96
6.27
23000
36
863
教材P36T2
2.一个长方体包装盒,从里面量长28cm,宽20cm,体积为11.76dm3。爸爸想用它包装一件长25cm,宽16cm,高18cm的玻璃器皿,是否可以装得下?
想一想,能装下吗?
教材P36T2
2.一个长方体包装盒,从里面量长28cm,宽20cm,里面的体积为11.76dm3。爸爸想用它包装一件长25cm、宽16cm、高18cm的玻璃器皿,是否可以装得下?
11.76 dm3=11760 cm3
11760÷(28×20)=21(cm)
21>18
答:可以装下。
教材P36T3
3.花园小区为居民新安装了50个休息的凳子,凳面的长、宽、高分别是100cm、45cm、4.5cm,凳腿的长、宽、高分别是45cm、5cm、35cm。做这些凳子至少用了混凝土多少方?
教材P36T3
3.花园小区为居民新安装了50个休息的凳子,凳面的长、宽、高分别是100cm、45cm、4.5cm,凳腿的长、宽、高分别是45cm、5cm、35cm。做这些凳子至少用了混凝土多少方?
(100×45×4.5+45×5×35×2)×50
=1800000(cm3)=1.8(m3)=1.8(方)
答:做这些凳子至少用了混凝土1.8方。
教材P36T4
4.“六一”儿童节前,全市的小学生代表用棱长3cm的正方体塑料拼插积木在广场中央搭起了一面长6m、高2.7m、厚6cm的奥运心愿墙,这面墙一共用了多少块积木?
教材P36T4
4.“六一”儿童节前,全市的小学生代表用棱长3cm的正方体塑料拼插积木在广场中央搭起了一面长6m、高2.7m、厚6cm的奥运心愿墙,这面墙一共用了多少块积木?
6 m=600 cm 2.7 m=270 cm
600×270×6÷(3×3×3)=36000(块)
答:这面墙一共用了36000块积木。
教材P36T5
5.学校运来7.6m 的沙子,铺在一个长5m、宽38dm的沙坑里,可以铺多厚?
h=V÷a÷b
根据V=abh,有:
=7.6÷5÷3.8
=0.4(米)
38分米=3.8米
答:可以铺0.4米厚。
教材P36T6
6.请你圈出每组数据中与其他数据不相等的那个数。
(1)5.08 m3 50800 cm3
5080 dm3 5080000 cm3
教材P36T6翼
6.请你圈出每组数据中与其他数据不相等的那个数。
(2)6039dm2 6.039m2
603900cm2 60.39m2
教材P36T6
6.请你圈出每组数据中与其他数据不相等的那个数。
(3)1500cm 1500dm
15m 150dm
教材P37T7
7.一个长方体的无盖水族箱,长是6m,宽是60cm,高是1.5m。这个水族箱占地面积有多大?需要用多少平方米的玻璃?它的体积是多少?
教材P37T7
7.一个长方体的无盖水族箱,长是6m,宽是60cm,高是1.5m。这个水族箱占地面积有多大?需要用多少平方米的玻璃?它的体积是多少?
占地面积:
60厘米=0.6米
6×0.6=3.6(平方米)
答:这个水族箱占地3.6平方米。
教材P37T7
7.一个长方体的无盖水族箱,长是6m,宽是60cm,高是1.5m。这个水族箱占地面积有多大?需要用多少平方米的玻璃?它的体积是多少?
玻璃:
6×0.6+6×1.5×2+1.5×0.6×2
=3.6+18+1.8
=23.4(平方米)
答:这个水族箱需要23.4平方米的玻璃。
教材P37T7
7.一个长方体的无盖水族箱,长是6m,宽是60cm,高是1.5m。这个水族箱占地面积有多大?需要用多少平方米的玻璃?它的体积是多少?
体积:V=abh
答:这个水族箱的体积是5.4立方米。
=6×0.6×1.5
=5.4(立方米)
教材P37T9
1.茶厂工人将长、宽各为20cm,高为10cm的长方体茶盒装入棱长为30cm的正方体纸箱,最多能装几盒?怎样才能装下?
教材P37T9
求能装几盒,用纸箱体积除以茶盒体积就行了。
教材P37T9
这样做,行吗?
30 ×30 ×30 ÷(20 ×20 ×10)
=27000 ÷4000
=6.75(个)
≈6(个)
教材P37T9
这样做不行!这不符合实际情况。
教材P37T9
最多能装5盒。其中3盒摞在一起,靠一个角码放,另外2个竖起,放在空余位置。
教材P37T9
求最多能装几盒,不能直接用纸箱体积除以茶盒体积,要根据实际情况进行分析。由于茶盒高10厘米,而纸箱棱长为30厘米,所以先考虑用3个茶盒摞起来,这样充分利用空间。纸箱所剩空间不能完全利用,长、宽各剩10厘米,只能考虑让茶盒竖起码放,只能再放2个。所以最多能装5盒。
把棱长为1m的正方体切割成棱长是1㎝的小正方体,把这些小正方体一个挨一个地连起来,可以排多长?
1m = 1000000 cm ,
1000000个小正方体一个挨一个地连起来,可以排1000000cm,
1000000cm =10000m =10km。
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
