2021-2022学年沪科版七年级数学下册6.1.1平方根课件(第一课时 17张)
文档属性
| 名称 | 2021-2022学年沪科版七年级数学下册6.1.1平方根课件(第一课时 17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 197.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第1课时 平方根
6.1 平方根、立方根
知识回顾
1.我们现已学过哪些运算?
(加、减、乘、除、乘方五种)
2.加法与减法这两种运算之间有什么关系?乘法与除法之间有什么关系?
(互为逆运算)
思考与探索
1.一个数的平方是9,这个数是什么数?
2.一个数的平方是 ,这个数是多少?
3.填空:
①( )2 = 16 ②( )2 =
③ ( ) 2 = 0 ④( )2 = 0.49
±4
±0.5
0
±0.7
概念导入
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根。
例如:由于22=4,(-2)2=4,
(可以合写为±2).
所以4的平方根是2 和-2
典型例题
例1:求下列数的平方根;
(1)36的平方根是___________
(2)0.0081的平方根是___________
(3) 的平方根是___________
(4) 的平方根是___________
同步练习
1、求下列数的平方根;
(1)144的平方根是___________
(2) 的平方根是___________
(3) 的平方根是___________
(4) 的平方根是___________
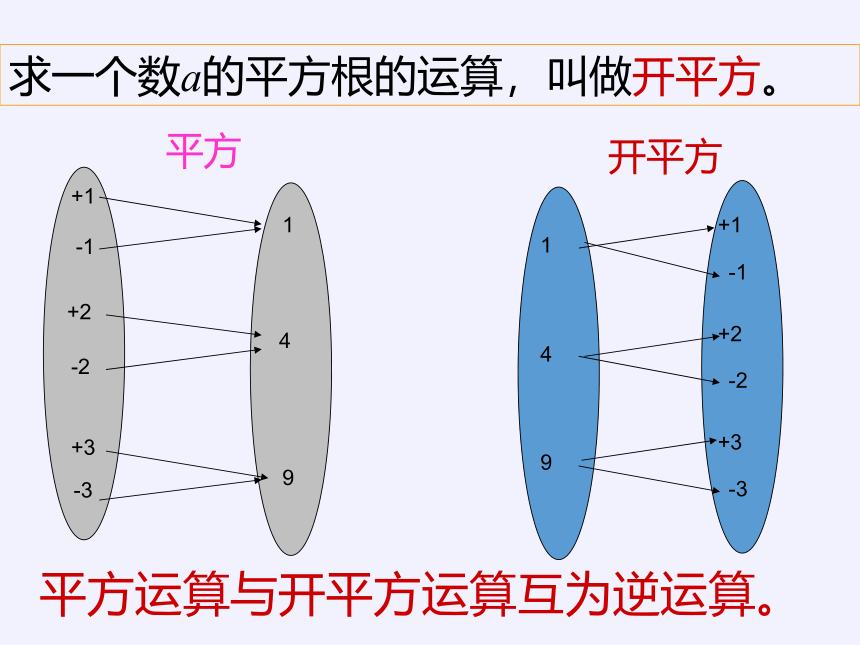
求一个数a的平方根的运算,叫做开平方。
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
平方运算与开平方运算互为逆运算。
知识探究
思考:5的平方根是________
一个正数 的正的平方根,用符号“ ”表示,
其中, 叫做被开方数,2叫做根指数。
“ ” 读作“二次根号 ”,根指数为2时,通常将这个2省略不写。如 可记作 ,读作“根号 ”。注意: 中, ≥ 0
一个正数 的负平方根,用符号 表示。
一个正数 的平方根可以合写为 “ ”
典型例题
(1)7的平方根是:
(2)9的平方根是:
(3)15的平方根是:
例2:
(4) 的平方根是:
正数的两个平方根互为相反数
典型例题
例3:一个正数的平方根是 2a+3和 a-6,
你能知道a是多少吗 这个正数是几?
解:由平方根的意义可得
所以这个正数是25
解得 a=1
(2a+3)+(a-6)=0
所以 2a+3=2+3=5
同步练习
2、一个正数的平方根是 2a-2和a-4 ,
你能知道a是多少吗 这个正数是几?
解:由平方根的意义可得
所以这个正数是4
解得 a=2
(2a-2)+(a-4)=0
所以 2a-2=4-2=2
知识探究
因为02=0,且任何不为0的数的平方都不等于0,所以0的平方根只有一个,它就是0本身。
即:
思考:负数有平方根吗?
因为正、负、0的平方都不是负数,所以负数没有平方根。
如: 无意义
例题
例、下列各数有平方根吗?如果有,求出它的
平方根,如果没有,说明道理。
同步练习
3、下列各式哪些有意义,哪些没
有意义?
课堂小结
1、什么是平方根?
2、正数、0、负数的平方根。
如果一个数的平方等于a,那么这个数叫做a的平方根
即a的平方根为
正数:由两个平方根,且两个平方根互为相反数;
0:0只有一个平方根,即0的平方根是0;
负数:负数没有平方根;
拓展练习
256
1、
a
3
5
1
2
|a|
-a
4
16
0
拓展练习
3.已知 , 求
的平方根。
解:由题意可得
第1课时 平方根
6.1 平方根、立方根
知识回顾
1.我们现已学过哪些运算?
(加、减、乘、除、乘方五种)
2.加法与减法这两种运算之间有什么关系?乘法与除法之间有什么关系?
(互为逆运算)
思考与探索
1.一个数的平方是9,这个数是什么数?
2.一个数的平方是 ,这个数是多少?
3.填空:
①( )2 = 16 ②( )2 =
③ ( ) 2 = 0 ④( )2 = 0.49
±4
±0.5
0
±0.7
概念导入
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根。
例如:由于22=4,(-2)2=4,
(可以合写为±2).
所以4的平方根是2 和-2
典型例题
例1:求下列数的平方根;
(1)36的平方根是___________
(2)0.0081的平方根是___________
(3) 的平方根是___________
(4) 的平方根是___________
同步练习
1、求下列数的平方根;
(1)144的平方根是___________
(2) 的平方根是___________
(3) 的平方根是___________
(4) 的平方根是___________
求一个数a的平方根的运算,叫做开平方。
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
平方运算与开平方运算互为逆运算。
知识探究
思考:5的平方根是________
一个正数 的正的平方根,用符号“ ”表示,
其中, 叫做被开方数,2叫做根指数。
“ ” 读作“二次根号 ”,根指数为2时,通常将这个2省略不写。如 可记作 ,读作“根号 ”。注意: 中, ≥ 0
一个正数 的负平方根,用符号 表示。
一个正数 的平方根可以合写为 “ ”
典型例题
(1)7的平方根是:
(2)9的平方根是:
(3)15的平方根是:
例2:
(4) 的平方根是:
正数的两个平方根互为相反数
典型例题
例3:一个正数的平方根是 2a+3和 a-6,
你能知道a是多少吗 这个正数是几?
解:由平方根的意义可得
所以这个正数是25
解得 a=1
(2a+3)+(a-6)=0
所以 2a+3=2+3=5
同步练习
2、一个正数的平方根是 2a-2和a-4 ,
你能知道a是多少吗 这个正数是几?
解:由平方根的意义可得
所以这个正数是4
解得 a=2
(2a-2)+(a-4)=0
所以 2a-2=4-2=2
知识探究
因为02=0,且任何不为0的数的平方都不等于0,所以0的平方根只有一个,它就是0本身。
即:
思考:负数有平方根吗?
因为正、负、0的平方都不是负数,所以负数没有平方根。
如: 无意义
例题
例、下列各数有平方根吗?如果有,求出它的
平方根,如果没有,说明道理。
同步练习
3、下列各式哪些有意义,哪些没
有意义?
课堂小结
1、什么是平方根?
2、正数、0、负数的平方根。
如果一个数的平方等于a,那么这个数叫做a的平方根
即a的平方根为
正数:由两个平方根,且两个平方根互为相反数;
0:0只有一个平方根,即0的平方根是0;
负数:负数没有平方根;
拓展练习
256
1、
a
3
5
1
2
|a|
-a
4
16
0
拓展练习
3.已知 , 求
的平方根。
解:由题意可得
