2021-2022学年沪科版七年级下册数学6.1.2立方根课件(16张)
文档属性
| 名称 | 2021-2022学年沪科版七年级下册数学6.1.2立方根课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 611.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 21:47:12 | ||
图片预览





文档简介
(共16张PPT)
第六章 实数
6.1.2 立方根
引入
如图,要做一个容积是 64 dm 的正方体木箱,问它的棱长是多少?
解:设正方体木箱的棱长为 x dm,
根据题意,有 x = 64.
这是“已知一个数的立方,求这个数”的问题.
新授
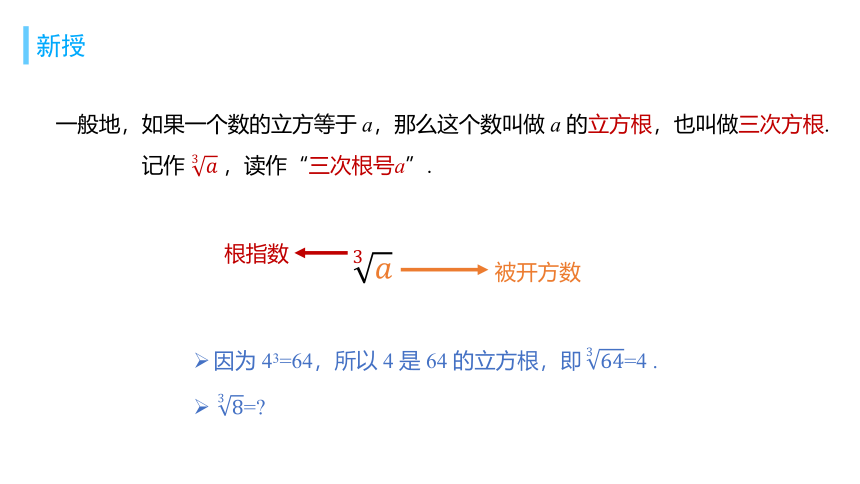
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根,也叫做三次方根.
如果 x3=a,那么 x 叫做 a 的立方根或三次方根.
在上面的问题中,因为 43=64,所以 4 是 64 的立方根.
新授
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根,也叫做三次方根.
记作 ,读作“三次根号a”.
根指数
被开方数
因为 43=64,所以 4 是 64 的立方根,即=4 .
=
新授
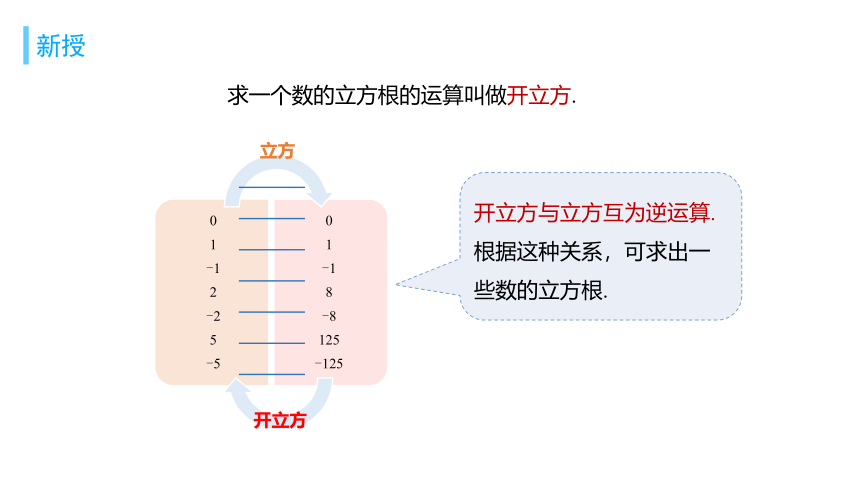
求一个数的立方根的运算叫做开立方.
立方
开立方
开立方与立方互为逆运算. 根据这种关系,可求出一些数的立方根.
新授
立方根
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根或三次方根.
开立方
求一个数的立方根的运算叫做开立方.
开立方与立方互为逆运算.
新授
因为 23 =8,所以 8 的立方根是( );
因为( )3 =0.064,所以 0.064 的立方根是( );
因为( )3 =0,所以 0 的立方根是( );
因为( )3 = 8,所以 8 的立方根是( );
因为( )3 = ,所以 的立方根是( ).
0
2
2
0
2
0.4
0.4
正数、0和负数的立方根各有什么特点?
新授
立方根的性质
1. 正数的立方根是正数.
2. 0 的立方根是 0.
3. 负数的立方根是负数.
一个数有几个立方根?
有且只有一个.
例题
例5 求下列各数的立方根:
(1) 27; (2) 64 ; (3)0.
解:(1)因为 3 =27,所以27的立方根是3,
即 =3
(2)因为 ,所以的立方根是 ,
即 =
(3)因为 0 =0,所以0的立方根是0,
即 =0
利用计算器可以求一个数的立方根或它的近似值.
例题
例6 用计算器求下列各数的立方根(精确到0.01):
(1) 2; (2) 7.797; (3) 17.456 ; (4)
解:(1)在计算器上依次按键:2ndf 2 =
显示结果是1.259 921 05,精确到0.01,得
(2)
(3)
(4)
练习
1. 判断是非:
3是27的立方根. ( )
64的立方根是±4. ( )
0的立方根是0. ( )
×
×
√
练习
2. 填表:
a 1 8 27 64
5 6 7 8 9 10
1
2
4
125
1000
216
343
512
729
3
练习
3.求下列各数的立方根:
(1) 1; (2) 1; (3)8; (4) 8.
解:(1)因为 1 =1,所以 1 的立方根是 1,
即 =1
(2)因为 ,所以的立方根是 ,
即 =
(3)因为 2 =8,所以 8 的立方根是 2,
即 =2
(4)因为 ,所以的立方根是 ,
即 =
练习
4. 用计算器计算(精确到 0.1):
(1) ; (2) ; (3) ; (4) .
解:(1) 3.0
(2)
(3)
(4) 0.3
总结
立方根
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根或三次方根.
开立方
求一个数的立方根的运算叫做开立方.
开立方与立方互为逆运算.
总结
立方根的性质
1. 正数的立方根是正数.
2. 0 的立方根是 0.
3. 负数的立方根是负数.
第六章 实数
6.1.2 立方根
引入
如图,要做一个容积是 64 dm 的正方体木箱,问它的棱长是多少?
解:设正方体木箱的棱长为 x dm,
根据题意,有 x = 64.
这是“已知一个数的立方,求这个数”的问题.
新授
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根,也叫做三次方根.
如果 x3=a,那么 x 叫做 a 的立方根或三次方根.
在上面的问题中,因为 43=64,所以 4 是 64 的立方根.
新授
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根,也叫做三次方根.
记作 ,读作“三次根号a”.
根指数
被开方数
因为 43=64,所以 4 是 64 的立方根,即=4 .
=
新授
求一个数的立方根的运算叫做开立方.
立方
开立方
开立方与立方互为逆运算. 根据这种关系,可求出一些数的立方根.
新授
立方根
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根或三次方根.
开立方
求一个数的立方根的运算叫做开立方.
开立方与立方互为逆运算.
新授
因为 23 =8,所以 8 的立方根是( );
因为( )3 =0.064,所以 0.064 的立方根是( );
因为( )3 =0,所以 0 的立方根是( );
因为( )3 = 8,所以 8 的立方根是( );
因为( )3 = ,所以 的立方根是( ).
0
2
2
0
2
0.4
0.4
正数、0和负数的立方根各有什么特点?
新授
立方根的性质
1. 正数的立方根是正数.
2. 0 的立方根是 0.
3. 负数的立方根是负数.
一个数有几个立方根?
有且只有一个.
例题
例5 求下列各数的立方根:
(1) 27; (2) 64 ; (3)0.
解:(1)因为 3 =27,所以27的立方根是3,
即 =3
(2)因为 ,所以的立方根是 ,
即 =
(3)因为 0 =0,所以0的立方根是0,
即 =0
利用计算器可以求一个数的立方根或它的近似值.
例题
例6 用计算器求下列各数的立方根(精确到0.01):
(1) 2; (2) 7.797; (3) 17.456 ; (4)
解:(1)在计算器上依次按键:2ndf 2 =
显示结果是1.259 921 05,精确到0.01,得
(2)
(3)
(4)
练习
1. 判断是非:
3是27的立方根. ( )
64的立方根是±4. ( )
0的立方根是0. ( )
×
×
√
练习
2. 填表:
a 1 8 27 64
5 6 7 8 9 10
1
2
4
125
1000
216
343
512
729
3
练习
3.求下列各数的立方根:
(1) 1; (2) 1; (3)8; (4) 8.
解:(1)因为 1 =1,所以 1 的立方根是 1,
即 =1
(2)因为 ,所以的立方根是 ,
即 =
(3)因为 2 =8,所以 8 的立方根是 2,
即 =2
(4)因为 ,所以的立方根是 ,
即 =
练习
4. 用计算器计算(精确到 0.1):
(1) ; (2) ; (3) ; (4) .
解:(1) 3.0
(2)
(3)
(4) 0.3
总结
立方根
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根或三次方根.
开立方
求一个数的立方根的运算叫做开立方.
开立方与立方互为逆运算.
总结
立方根的性质
1. 正数的立方根是正数.
2. 0 的立方根是 0.
3. 负数的立方根是负数.
