2021-2022学年人教版七年级数学下册5.1.2垂线同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.1.2垂线同步练习题(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 329.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 21:47:14 | ||
图片预览

文档简介
5.1.2 垂线
一、单项选择题
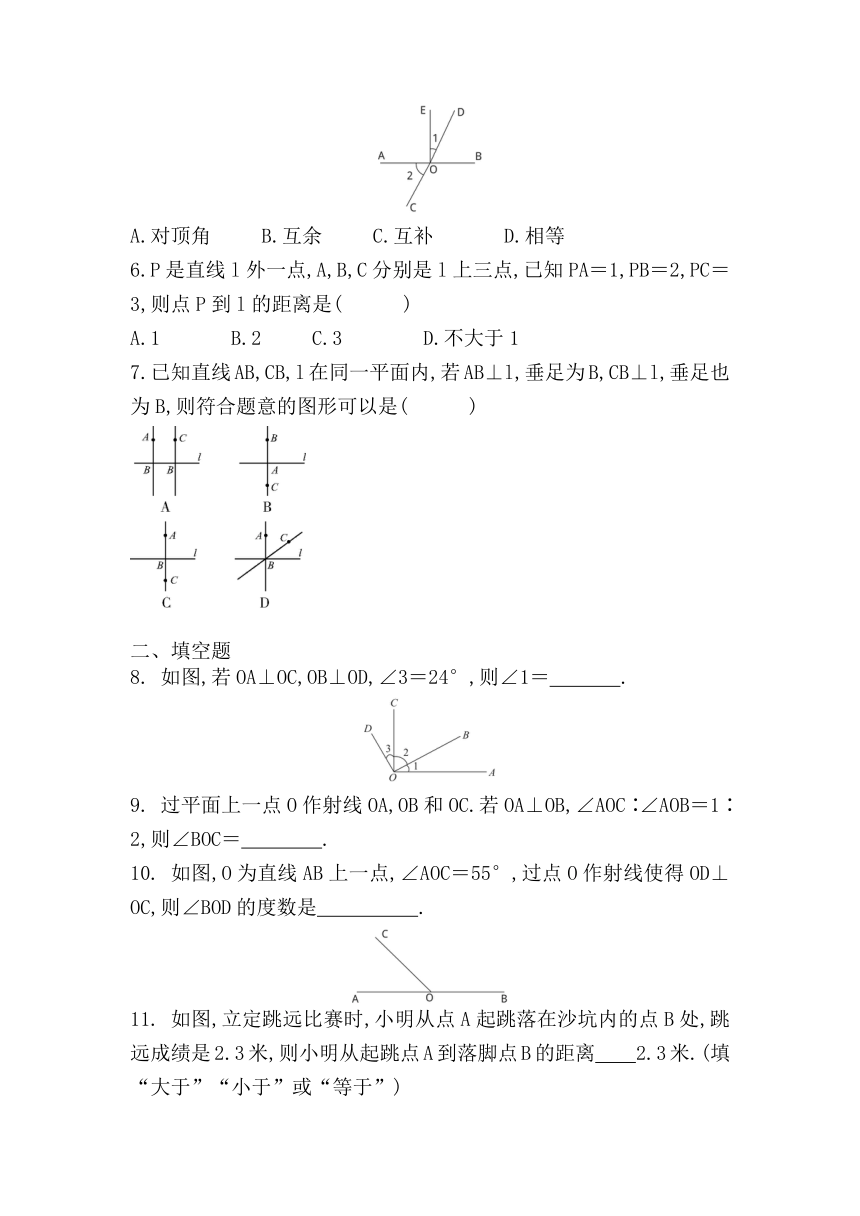
1.如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
2.经过直线l外一点P画l的垂线CD,下列各图操作正确的是( )
3.如图,经过直线l外一点A画l的垂线,能画出( )
A.1条 B.2条 C.3条 D.4条
4.如图,∠BAC=90°,AD⊥BC,则下列结论错误的是( )
A.线段AB是点B到AC的垂线段 B.线段AC是点C到AB的垂线段
C.线段AD是点D到AC的垂线段 D.线段BD是点B到AD的垂线段
5.如图,直线AB,CD相交于点O,OE⊥AB于点O,则图中∠1与∠2的关系是( )
A.对顶角 B.互余 C.互补 D.相等
6.P是直线l外一点,A,B,C分别是l上三点,已知PA=1,PB=2,PC=3,则点P到l的距离是( )
A.1 B.2 C.3 D.不大于1
7.已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
二、填空题
8. 如图,若OA⊥OC,OB⊥OD,∠3=24°,则∠1= .
9. 过平面上一点O作射线OA,OB和OC.若OA⊥OB,∠AOC∶∠AOB=1∶2,则∠BOC= .
10. 如图,O为直线AB上一点,∠AOC=55°,过点O作射线使得OD⊥OC,则∠BOD的度数是 .
11. 如图,立定跳远比赛时,小明从点A起跳落在沙坑内的点B处,跳远成绩是2.3米,则小明从起跳点A到落脚点B的距离 2.3米.(填“大于”“小于”或“等于”)
三、解答题
12. 如图,O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.若∠AOB=130°,求∠EOF的度数.
13. 如图,直线a是一条铁路,A点表示铁路上的火车站;直线b是一条河流,B点表示河流边的码头.请解决下列问题:
(1)从火车站到码头怎样走最近 请利用画图来说明.
(2)从码头到铁路怎样走最近 请利用画图来说明.
14. 如图,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=25°.求∠COG的度数.
15. 如图,平原上有A,B,C,D四个村庄,为解决当地的缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄的距离之和最小.
(2)计划把河水引入蓄水池H中,怎样开渠最短 并说明理由.
答案:
一、
1-7 ADACB DC
二、
8. 24°
9. 135°或45°
10. 35°或145°
11. 大于
三、
12. 解:因为∠AOB=130°,EO是∠AOB的平分线,
所以∠BOE=∠AOB=65°.
因为OB⊥OF,所以∠BOF=90°,
所以∠EOF=∠BOF-∠BOE=90°-65°=25°.
13. 解:(1)如图所示,连接AB,沿线段AB走最近.
(2)如图所示,过点B作直线a的垂线,垂足为D,沿线段BD走最近.
14. 解:因为∠FOD与∠COE互为对顶角,
所以∠COE=∠FOD=25°.
因为AB⊥CD,所以∠AOC=90°,
所以∠AOE=∠AOC+∠COE=115°.
又因为OG平分∠AOE,
所以∠EOG=∠AOE=57.5°,
所以∠COG=∠EOG-∠COE=57.5°-25°=32.5°.
15. 解:(1)因为两点之间线段最短,所以连接AD,BC相交于点H,则点H即为蓄水池的位置,它到四个村庄的距离之和最小.图略.
(2)过点H作HG⊥EF,垂足为G,则应沿线段HG开渠.
理由:连接直线外一点与直线上各点的所有线段中,垂线段最短.
一、单项选择题
1.如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
2.经过直线l外一点P画l的垂线CD,下列各图操作正确的是( )
3.如图,经过直线l外一点A画l的垂线,能画出( )
A.1条 B.2条 C.3条 D.4条
4.如图,∠BAC=90°,AD⊥BC,则下列结论错误的是( )
A.线段AB是点B到AC的垂线段 B.线段AC是点C到AB的垂线段
C.线段AD是点D到AC的垂线段 D.线段BD是点B到AD的垂线段
5.如图,直线AB,CD相交于点O,OE⊥AB于点O,则图中∠1与∠2的关系是( )
A.对顶角 B.互余 C.互补 D.相等
6.P是直线l外一点,A,B,C分别是l上三点,已知PA=1,PB=2,PC=3,则点P到l的距离是( )
A.1 B.2 C.3 D.不大于1
7.已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
二、填空题
8. 如图,若OA⊥OC,OB⊥OD,∠3=24°,则∠1= .
9. 过平面上一点O作射线OA,OB和OC.若OA⊥OB,∠AOC∶∠AOB=1∶2,则∠BOC= .
10. 如图,O为直线AB上一点,∠AOC=55°,过点O作射线使得OD⊥OC,则∠BOD的度数是 .
11. 如图,立定跳远比赛时,小明从点A起跳落在沙坑内的点B处,跳远成绩是2.3米,则小明从起跳点A到落脚点B的距离 2.3米.(填“大于”“小于”或“等于”)
三、解答题
12. 如图,O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.若∠AOB=130°,求∠EOF的度数.
13. 如图,直线a是一条铁路,A点表示铁路上的火车站;直线b是一条河流,B点表示河流边的码头.请解决下列问题:
(1)从火车站到码头怎样走最近 请利用画图来说明.
(2)从码头到铁路怎样走最近 请利用画图来说明.
14. 如图,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=25°.求∠COG的度数.
15. 如图,平原上有A,B,C,D四个村庄,为解决当地的缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄的距离之和最小.
(2)计划把河水引入蓄水池H中,怎样开渠最短 并说明理由.
答案:
一、
1-7 ADACB DC
二、
8. 24°
9. 135°或45°
10. 35°或145°
11. 大于
三、
12. 解:因为∠AOB=130°,EO是∠AOB的平分线,
所以∠BOE=∠AOB=65°.
因为OB⊥OF,所以∠BOF=90°,
所以∠EOF=∠BOF-∠BOE=90°-65°=25°.
13. 解:(1)如图所示,连接AB,沿线段AB走最近.
(2)如图所示,过点B作直线a的垂线,垂足为D,沿线段BD走最近.
14. 解:因为∠FOD与∠COE互为对顶角,
所以∠COE=∠FOD=25°.
因为AB⊥CD,所以∠AOC=90°,
所以∠AOE=∠AOC+∠COE=115°.
又因为OG平分∠AOE,
所以∠EOG=∠AOE=57.5°,
所以∠COG=∠EOG-∠COE=57.5°-25°=32.5°.
15. 解:(1)因为两点之间线段最短,所以连接AD,BC相交于点H,则点H即为蓄水池的位置,它到四个村庄的距离之和最小.图略.
(2)过点H作HG⊥EF,垂足为G,则应沿线段HG开渠.
理由:连接直线外一点与直线上各点的所有线段中,垂线段最短.
