2021-2022学年苏科版九年级数学下册6.2黄金分割课后提升练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册6.2黄金分割课后提升练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 498.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 21:51:10 | ||
图片预览



文档简介
6.2黄金分割
一、选择题
1、一条线段的黄金分割点有( )
A.1个 B.2个 C.3个 D.无数个
2.小明同学发现自己一本书的宽与长之比是黄金比约为0.618.已知这本书的长为20cm,则它的宽约为( )
A.12.36cm B.13.6cm C.32.386cm D.7.64cm
3.(2019 兴化市二模)已知P为线段AB的黄金分割点,且AP>PB,则( )
A.AP2+BP2=AB2 B.BP2=AP AB
C.AP2=AB BP D.AB2=AP PB
4.如图,若点P是线段AB的黄金分割点,AP>BP,AB=2,则AP的长度是( )
A. B. C. D.
5、点B是线段AC的黄金分割点,且ABBC.若AC=4,则BC的长为( )
A. B. C. D.
6、若点为线段的黄金分割点,且,则下列各式中不正确的是( )
A. B.
C. D.
7.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165cm,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
A.4cm B.6cm C.8cm D.10cm
8.如图,点B在线段AC上,且,设AC=2,则AB的长为( )
A. B. C. D.
9.如果一个矩形的宽(即短边)与长(即长边)之比是,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E、F、G、H分别为线段AD、BC、AB、EF的中点,则图中黄金矩形的个数是( )
A.5个 B.4个 C.3个 D.2个
10、我们把宽与长的比值等于黄金比例的矩形称为黄金矩形.如图,在黄金矩形的边上取一点,使得,连接,则等于
A. B. C. D.
二、填空题
11、已知点是线段的黄金分割点,.若.则 (结果保留根号).
12.若线段c是线段a,b的比例中项,且a=4 cm,b=25 cm,则c=____cm.
13.如图是一种贝壳的示意图,点C分线段AB近似于黄金分割比.已知AB=12 cm,则AC的长约为____cm(结果精确到0.1 cm).
14.如图连结正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为.若AB=,则MN=____.
15、某公司生产一种新型手杖,其长为,现要在黄金分割点位置安放一个小装饰品,装饰品离手杖上端的距离为 .(注:该装饰品离手杖的上端较近,结果保留根号)
三、解答题
16、宽与长的比是的矩形叫做黄金矩形.现将构造黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
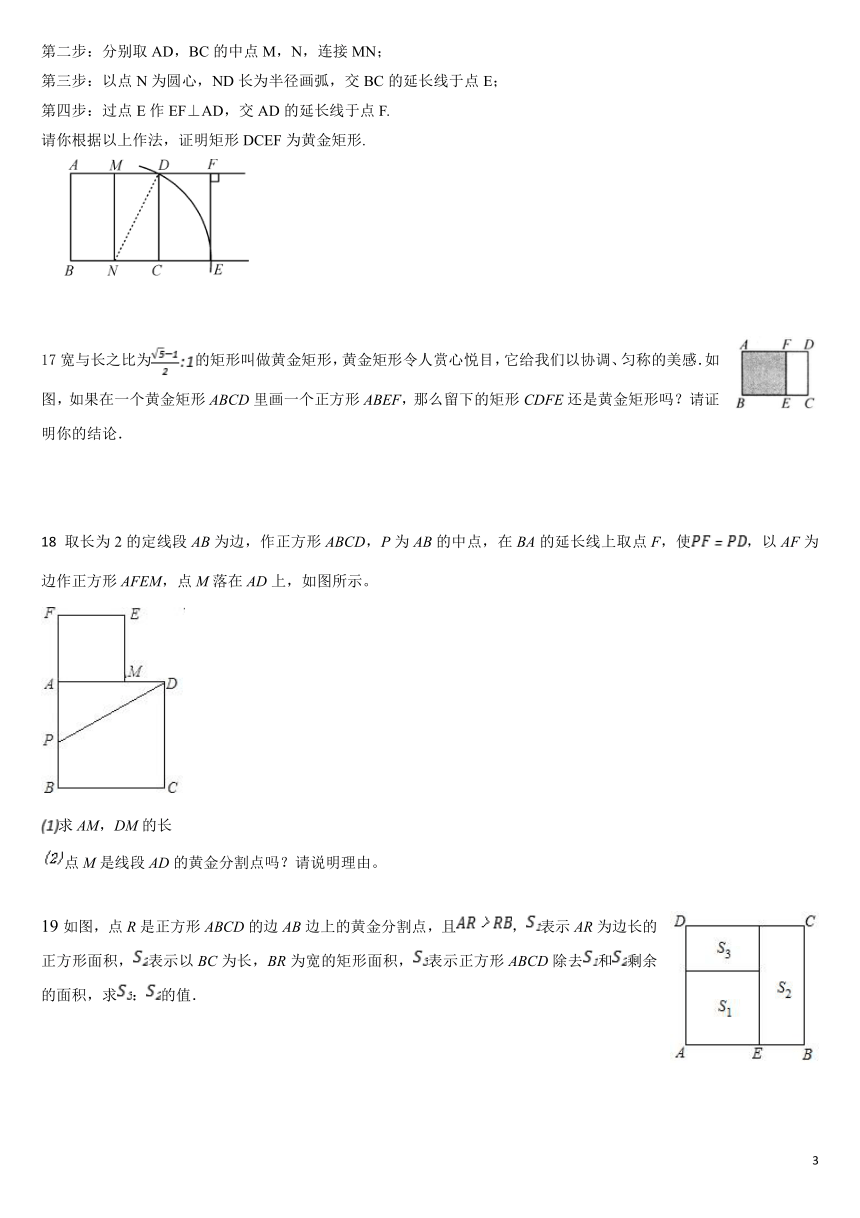
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于点F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
17宽与长之比为的矩形叫做黄金矩形,黄金矩形令人赏心悦目,它给我们以协调、匀称的美感.如图,如果在一个黄金矩形ABCD里画一个正方形ABEF,那么留下的矩形CDFE还是黄金矩形吗?请证明你的结论.
18 取长为2的定线段AB为边,作正方形ABCD,P为AB的中点,在BA的延长线上取点F,使,以AF为边作正方形AFEM,点M落在AD上,如图所示。
求AM,DM的长
点M是线段AD的黄金分割点吗?请说明理由。
19如图,点R是正方形ABCD的边AB边上的黄金分割点,且,表示AR为边长的正方形面积,表示以BC为长,BR为宽的矩形面积,表示正方形ABCD除去和剩余的面积,求:的值.
20 维纳斯女神相于1820年在密罗斯岛被发现,在多方的争夺神像的混战中,雕像的双臂被砸断,但是这一缺憾并不影响世人对其的无限推崇,至今她已经成为优雅、高贵的代名词.不仅如此,她的身材比例也符合黄金分割,也可以说是因为数学之美才赋予了女神之美.请你用尺规作图在中轴虚线上作出黄金分割点,并证明你的结论.
21、如图,点C将线段AB分成两部分,若AC2=BC AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于
A(3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
1. B 2. A 3.C 4. A 5. B 6. A7.C 8.C 9. C 10.B
11、:.
12.10
13. 2
14 -2.
15、.
16、宽与长的比是的矩形叫做黄金矩形.现将构造黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于点F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
证明:在正方形ABCD中,设AB=2a.
∵N为BC的中点,
∴NC=BC=a.
在Rt△DNC中,
ND===a.
又∵NE=ND,∴CE=NE-NC=(-1)a.
∴==,即矩形DCEF为黄金矩形.
17.【答案】解:留下的矩形CDFE是黄金矩形.
证明:四边形ABEF是正方形,
,
又,
,
矩形CDFE是黄金矩形.
18.【答案】解:在中,,,
由勾股定理知,
,
.
,
,
,
点M是线段AD的黄金分割点.
【解析】
【分析】
本题考查了勾股定理,黄金分割,根据已知条件结合勾股定理求得线段的长,能够用黄金分割点的定义进行证明.
要求AM的长,即是求AF的长,只需求得PF的长,根据勾股定理进行计算PD的长就可;要求DM的长,只需就可;
根据黄金分割点的定义,只需证明.
19.【答案】解:如图,设,
点E是正方形ABCD的边AB边上的黄金分割点,且,
,
,
::
:
.
故答案为:.
20.【答案】作法:如图,
过点C作,使;
在BC截取;
以点B为圆心,BE为半径画弧,交AB于点D.
点D即为所求.
证明:设AB的长度为x,作,使,
在中,
,
,
,
,
图中点D为所求黄金分割点.
21、如图,点C将线段AB分成两部分,若AC2=BC AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于
A(3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
【分析】(Ⅰ)根据对称轴确定a和b的关系,再根据已知条件即可求解;
(Ⅱ)根据抛物线的顶点坐标确定x0的值,再根据黄金分割的定义即可判断.
【解析】(Ⅰ)∵黄金抛物线的对称轴是直线x=2,∴=2,
∴b=﹣4a,又b2=ac, ∴16a2=ac.
且与y轴交于点(0,8),∴c=8. ∴a=,b=﹣2.
∴y=x2﹣2x+8=(x﹣2)2+6,
∵>0,∴y有最小值为6.答:y的最小值为6.
(Ⅱ)原点是线段AB的黄金分割点.理由如下:
∵黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),
把它向下平移后与x轴交于A(3,0),B(x0,0),
∴x0=﹣1-.
∴OA=3+,OB=1+,AB=4+2.
OA2=(3+)2=14+6.
OB AB=(1+)(4+2)=14+6.
∴OA2=OB AB.
答:原点是线段AB的黄金分割点.
一、选择题
1、一条线段的黄金分割点有( )
A.1个 B.2个 C.3个 D.无数个
2.小明同学发现自己一本书的宽与长之比是黄金比约为0.618.已知这本书的长为20cm,则它的宽约为( )
A.12.36cm B.13.6cm C.32.386cm D.7.64cm
3.(2019 兴化市二模)已知P为线段AB的黄金分割点,且AP>PB,则( )
A.AP2+BP2=AB2 B.BP2=AP AB
C.AP2=AB BP D.AB2=AP PB
4.如图,若点P是线段AB的黄金分割点,AP>BP,AB=2,则AP的长度是( )
A. B. C. D.
5、点B是线段AC的黄金分割点,且ABBC.若AC=4,则BC的长为( )
A. B. C. D.
6、若点为线段的黄金分割点,且,则下列各式中不正确的是( )
A. B.
C. D.
7.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165cm,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
A.4cm B.6cm C.8cm D.10cm
8.如图,点B在线段AC上,且,设AC=2,则AB的长为( )
A. B. C. D.
9.如果一个矩形的宽(即短边)与长(即长边)之比是,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E、F、G、H分别为线段AD、BC、AB、EF的中点,则图中黄金矩形的个数是( )
A.5个 B.4个 C.3个 D.2个
10、我们把宽与长的比值等于黄金比例的矩形称为黄金矩形.如图,在黄金矩形的边上取一点,使得,连接,则等于
A. B. C. D.
二、填空题
11、已知点是线段的黄金分割点,.若.则 (结果保留根号).
12.若线段c是线段a,b的比例中项,且a=4 cm,b=25 cm,则c=____cm.
13.如图是一种贝壳的示意图,点C分线段AB近似于黄金分割比.已知AB=12 cm,则AC的长约为____cm(结果精确到0.1 cm).
14.如图连结正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为.若AB=,则MN=____.
15、某公司生产一种新型手杖,其长为,现要在黄金分割点位置安放一个小装饰品,装饰品离手杖上端的距离为 .(注:该装饰品离手杖的上端较近,结果保留根号)
三、解答题
16、宽与长的比是的矩形叫做黄金矩形.现将构造黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于点F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
17宽与长之比为的矩形叫做黄金矩形,黄金矩形令人赏心悦目,它给我们以协调、匀称的美感.如图,如果在一个黄金矩形ABCD里画一个正方形ABEF,那么留下的矩形CDFE还是黄金矩形吗?请证明你的结论.
18 取长为2的定线段AB为边,作正方形ABCD,P为AB的中点,在BA的延长线上取点F,使,以AF为边作正方形AFEM,点M落在AD上,如图所示。
求AM,DM的长
点M是线段AD的黄金分割点吗?请说明理由。
19如图,点R是正方形ABCD的边AB边上的黄金分割点,且,表示AR为边长的正方形面积,表示以BC为长,BR为宽的矩形面积,表示正方形ABCD除去和剩余的面积,求:的值.
20 维纳斯女神相于1820年在密罗斯岛被发现,在多方的争夺神像的混战中,雕像的双臂被砸断,但是这一缺憾并不影响世人对其的无限推崇,至今她已经成为优雅、高贵的代名词.不仅如此,她的身材比例也符合黄金分割,也可以说是因为数学之美才赋予了女神之美.请你用尺规作图在中轴虚线上作出黄金分割点,并证明你的结论.
21、如图,点C将线段AB分成两部分,若AC2=BC AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于
A(3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
1. B 2. A 3.C 4. A 5. B 6. A7.C 8.C 9. C 10.B
11、:.
12.10
13. 2
14 -2.
15、.
16、宽与长的比是的矩形叫做黄金矩形.现将构造黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于点F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
证明:在正方形ABCD中,设AB=2a.
∵N为BC的中点,
∴NC=BC=a.
在Rt△DNC中,
ND===a.
又∵NE=ND,∴CE=NE-NC=(-1)a.
∴==,即矩形DCEF为黄金矩形.
17.【答案】解:留下的矩形CDFE是黄金矩形.
证明:四边形ABEF是正方形,
,
又,
,
矩形CDFE是黄金矩形.
18.【答案】解:在中,,,
由勾股定理知,
,
.
,
,
,
点M是线段AD的黄金分割点.
【解析】
【分析】
本题考查了勾股定理,黄金分割,根据已知条件结合勾股定理求得线段的长,能够用黄金分割点的定义进行证明.
要求AM的长,即是求AF的长,只需求得PF的长,根据勾股定理进行计算PD的长就可;要求DM的长,只需就可;
根据黄金分割点的定义,只需证明.
19.【答案】解:如图,设,
点E是正方形ABCD的边AB边上的黄金分割点,且,
,
,
::
:
.
故答案为:.
20.【答案】作法:如图,
过点C作,使;
在BC截取;
以点B为圆心,BE为半径画弧,交AB于点D.
点D即为所求.
证明:设AB的长度为x,作,使,
在中,
,
,
,
,
图中点D为所求黄金分割点.
21、如图,点C将线段AB分成两部分,若AC2=BC AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于
A(3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
【分析】(Ⅰ)根据对称轴确定a和b的关系,再根据已知条件即可求解;
(Ⅱ)根据抛物线的顶点坐标确定x0的值,再根据黄金分割的定义即可判断.
【解析】(Ⅰ)∵黄金抛物线的对称轴是直线x=2,∴=2,
∴b=﹣4a,又b2=ac, ∴16a2=ac.
且与y轴交于点(0,8),∴c=8. ∴a=,b=﹣2.
∴y=x2﹣2x+8=(x﹣2)2+6,
∵>0,∴y有最小值为6.答:y的最小值为6.
(Ⅱ)原点是线段AB的黄金分割点.理由如下:
∵黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),
把它向下平移后与x轴交于A(3,0),B(x0,0),
∴x0=﹣1-.
∴OA=3+,OB=1+,AB=4+2.
OA2=(3+)2=14+6.
OB AB=(1+)(4+2)=14+6.
∴OA2=OB AB.
答:原点是线段AB的黄金分割点.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
