2021-2022学年北师大版数学七年级下册4.1认识三角形课件(17张)
文档属性
| 名称 | 2021-2022学年北师大版数学七年级下册4.1认识三角形课件(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 21:51:13 | ||
图片预览




文档简介
(共17张PPT)
2022
4.1 认识三角形
学习目标
1.认识三角形的高,能画任意三角形的高,了解三角形三条高所在直线交于一点;
2.学会用数学知识解决实际问题的能力,发展应用和自主探究意识,培养学生的动手实践能力, 与合作精神,树立学好数学的信心
新课导入
垂线:
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫作另外一条直线的垂线.
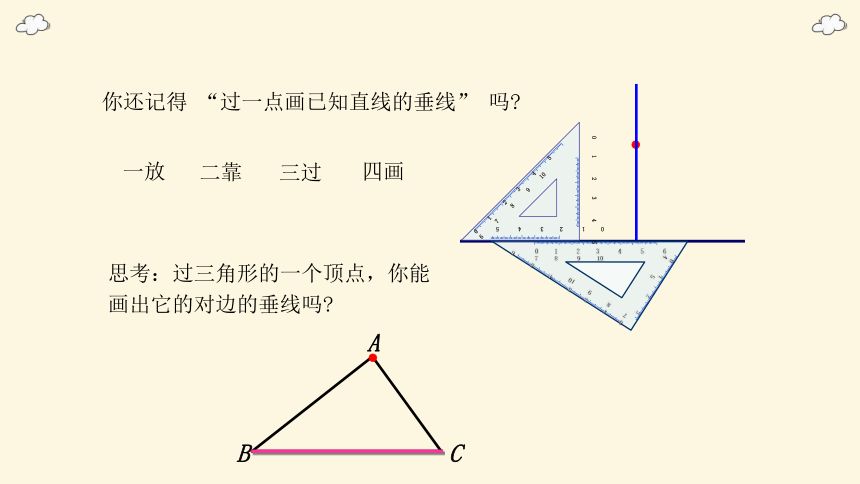
你还记得 “过一点画已知直线的垂线” 吗
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
一放
二靠
三过
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
四画
思考:过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
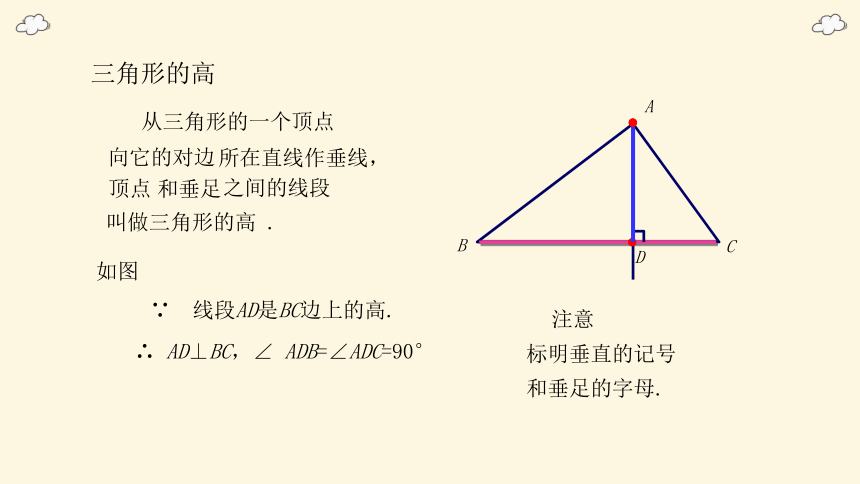
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高 .
如图
∵ 线段AD是BC边上的高.
∴ AD⊥BC,∠ ADB=∠ADC=90°
和垂足的字母.
注意
标明垂直的记号
(1) 你能画出锐角三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
(3) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
如图所示;
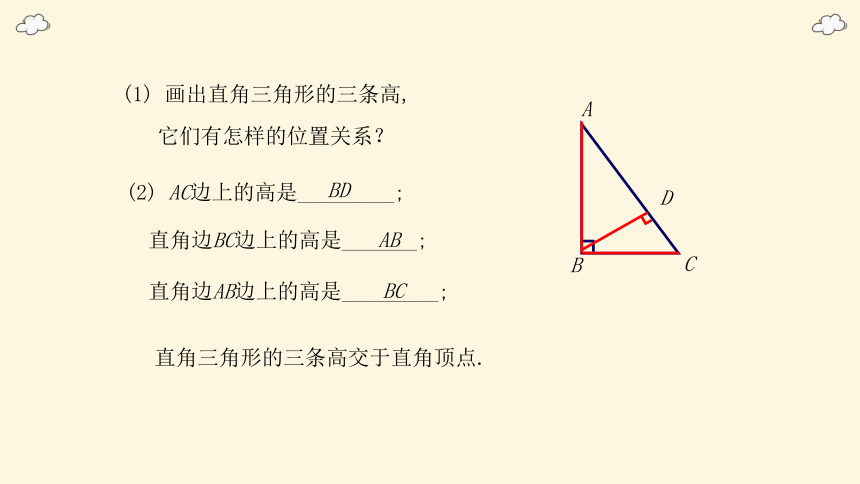
直角边BC边上的高是_______;
直角边AB边上的高是_________;
(2) AC边上的高是_________;
A
B
C
(1) 画出直角三角形的三条高,
AB
BC
它们有怎样的位置关系?
D
直角三角形的三条高交于直角顶点.
BD
(1) 你能画出钝角三角形的三条高吗?
(2) AC边上的高呢?
AB边上呢?
BC边上呢?
BF
CE
AD
(3)钝角三角形的三条高交于一点吗?
A
B
C
D
F
O
E
(4)它们所在的直线交于一点吗?
钝角三角形的三条高不相交于一点;
钝角三角形的三条高所在直线交于一点.
三角形的三条高的特征:
三角形的三条高所在直线交于一点
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量 3 1 1
高之间是否相交 相交 相交 不相交
高所在的直线是否相交 相交 相交 相交
三条高所在直线的 交点的位置 三角形内部 直角顶点 三角形外部
例1、如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A
B
C
D
A
例2、如图,已知AD,AE分别是Rt△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°.求:
解:(1)∵S△ABC=AB·AC= ×6×8=24 cm2,
∴S△ABC= AD·BC=24 cm2,
∵BC=10 cm, ∴AD=4.8 cm.
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
(2)S△ABE= BE·AD= ·(BC)·AD= S△ABC=12 cm2.
(3)将△ACE和△ABE的周长分别记为C△ACE和C△ABE,
则C△ACE-C△ABE=AC+CE+AE-(AB+BE+AE)=AC-AB=8-6=2 cm.
例3、如图,AF,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,求∠DAF的度数.
解: ∵∠B=36°,∠C=76°,
∴∠BAC=180°-∠B-∠C=180°-36°-76°=68°.
又AD平分∠BAC,
∴∠BAD=∠BAC=34°,
∴∠ADB=180°-∠B-∠BAD=110°,
∴∠ADF=180°-110°=70°,
∴∠DAF=90°-70°=20°.
1. 如图,在△ABC中,BC边上的高为( )
A.BE B.AE C.BF D.CF
B
2.一定在三角形内部的线段是( )
A.三角形的角平分线、中线、高 B.三角形的角平分线、中线
C.三角形的三条高线 D.以上都不对
B
随堂练习
3.如图, CF是△ABC的高,AB=5,S△ABC=15,则CF=________.
6
4.已知Rt△ABC中,∠BAC=90°,AD是△ABC的高,∠BAD=80°,则∠C=_______.
80°
5.如图,在△ABC中,AD,AE分别是边BC上的中线和高,AE=2 cm,S△ABD=1.5 cm2,求BC和CD的长.
解:∵ AD,AE分别是边BC上的中线和高,AE=2 cm,S△ABD=1.5 cm2,
∴ S△ADC=S△ABD=1.5 cm2,
∴ ·AE·CD=1.5,∴ ×2×CD=1.5,
∴ CD=1.5 cm,∴BC=2×1.5=3 cm.
综上所述,BC和CD的长分别是3 cm和1.5 cm.
6.如图, AD是△ABC的高,BE平分∠ABC,交AD于E,若∠C=70°,∠BED=64°,求∠BAC的度数.
解:在△BED中,
∵ AD⊥BC,∠BED=64°,
∴ ∠EBD=90°-64°=26°.
又∵BE平分∠ABC,
∴∠ABC=2∠EBD=52°.
∵∠C=70°,
∴在△ABC中,∠BAC=180°-52°-70°=58°.
课堂小结
三角形的高
高的定义
高的特征
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高交于直角顶点.
钝角三角形的三条高所在直线交于一点.
2022
4.1 认识三角形
学习目标
1.认识三角形的高,能画任意三角形的高,了解三角形三条高所在直线交于一点;
2.学会用数学知识解决实际问题的能力,发展应用和自主探究意识,培养学生的动手实践能力, 与合作精神,树立学好数学的信心
新课导入
垂线:
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫作另外一条直线的垂线.
你还记得 “过一点画已知直线的垂线” 吗
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
一放
二靠
三过
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
四画
思考:过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高 .
如图
∵ 线段AD是BC边上的高.
∴ AD⊥BC,∠ ADB=∠ADC=90°
和垂足的字母.
注意
标明垂直的记号
(1) 你能画出锐角三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
(3) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
如图所示;
直角边BC边上的高是_______;
直角边AB边上的高是_________;
(2) AC边上的高是_________;
A
B
C
(1) 画出直角三角形的三条高,
AB
BC
它们有怎样的位置关系?
D
直角三角形的三条高交于直角顶点.
BD
(1) 你能画出钝角三角形的三条高吗?
(2) AC边上的高呢?
AB边上呢?
BC边上呢?
BF
CE
AD
(3)钝角三角形的三条高交于一点吗?
A
B
C
D
F
O
E
(4)它们所在的直线交于一点吗?
钝角三角形的三条高不相交于一点;
钝角三角形的三条高所在直线交于一点.
三角形的三条高的特征:
三角形的三条高所在直线交于一点
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量 3 1 1
高之间是否相交 相交 相交 不相交
高所在的直线是否相交 相交 相交 相交
三条高所在直线的 交点的位置 三角形内部 直角顶点 三角形外部
例1、如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A
B
C
D
A
例2、如图,已知AD,AE分别是Rt△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°.求:
解:(1)∵S△ABC=AB·AC= ×6×8=24 cm2,
∴S△ABC= AD·BC=24 cm2,
∵BC=10 cm, ∴AD=4.8 cm.
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
(2)S△ABE= BE·AD= ·(BC)·AD= S△ABC=12 cm2.
(3)将△ACE和△ABE的周长分别记为C△ACE和C△ABE,
则C△ACE-C△ABE=AC+CE+AE-(AB+BE+AE)=AC-AB=8-6=2 cm.
例3、如图,AF,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,求∠DAF的度数.
解: ∵∠B=36°,∠C=76°,
∴∠BAC=180°-∠B-∠C=180°-36°-76°=68°.
又AD平分∠BAC,
∴∠BAD=∠BAC=34°,
∴∠ADB=180°-∠B-∠BAD=110°,
∴∠ADF=180°-110°=70°,
∴∠DAF=90°-70°=20°.
1. 如图,在△ABC中,BC边上的高为( )
A.BE B.AE C.BF D.CF
B
2.一定在三角形内部的线段是( )
A.三角形的角平分线、中线、高 B.三角形的角平分线、中线
C.三角形的三条高线 D.以上都不对
B
随堂练习
3.如图, CF是△ABC的高,AB=5,S△ABC=15,则CF=________.
6
4.已知Rt△ABC中,∠BAC=90°,AD是△ABC的高,∠BAD=80°,则∠C=_______.
80°
5.如图,在△ABC中,AD,AE分别是边BC上的中线和高,AE=2 cm,S△ABD=1.5 cm2,求BC和CD的长.
解:∵ AD,AE分别是边BC上的中线和高,AE=2 cm,S△ABD=1.5 cm2,
∴ S△ADC=S△ABD=1.5 cm2,
∴ ·AE·CD=1.5,∴ ×2×CD=1.5,
∴ CD=1.5 cm,∴BC=2×1.5=3 cm.
综上所述,BC和CD的长分别是3 cm和1.5 cm.
6.如图, AD是△ABC的高,BE平分∠ABC,交AD于E,若∠C=70°,∠BED=64°,求∠BAC的度数.
解:在△BED中,
∵ AD⊥BC,∠BED=64°,
∴ ∠EBD=90°-64°=26°.
又∵BE平分∠ABC,
∴∠ABC=2∠EBD=52°.
∵∠C=70°,
∴在△ABC中,∠BAC=180°-52°-70°=58°.
课堂小结
三角形的高
高的定义
高的特征
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高交于直角顶点.
钝角三角形的三条高所在直线交于一点.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
