2021-2022学年苏科版八年级数学下册9.3平行四边形强化训练(一)(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册9.3平行四边形强化训练(一)(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 683.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览



文档简介
2021-2022学年苏科版八年级数学下《9.3平行四边形》强化训练(一)
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共36分)
1.平行四边形不一定具有的特征是( )
A.内角和为360度 B.对角互补 C.邻角互补 D.对角相等
2.如图,在 ABCD中,AC=4 cm.若△ACD的周长是12 cm,则平行四边形ABCD的周长是( )
A.16 cm B.18 cm C.20 cm D.24 cm
第2题图 第3题图 第4题图 第5题图 第6题图
3.如图3,在 ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.1 B. C.2 D.3
4.如图,在平行四边形ABCD中,点E在边AB上,点F在边CD上,如果添加一个条件,使△ADE≌△CBF,那么添加的条件不能为( )
A.DE=BF B.AE=CF C.BE=DF D.∠ADE=∠CBF
5.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3 cm,直线b与c之间的距离是5 cm,那么直线a与c的距离是( )
A.2 cm B.8 cm C.8或2 cm D.不能确定
5.如图3,直线l1∥l2,△ABC的面积为10,则△DBC的面积( )
A.大于10 B.小于10 C.等于10 D.无法确定
6.如图所示,l1∥l2,AB∥CD,CE⊥l1,FG⊥l2,E,G为垂足,则下列说法中错误的是( )
A.CD>CE B.A,B两点间的距离就是线段AB的长
C.CE=FG D.l1,l2间的距离就是线段CD的长
7.如图,在 ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )
A.AB∥CD B.AB=CD C.AC=BD D.OA=OC
第7题图 第8题图 第9题图 第10题图 第11题图 第12题图
8.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13 B.17 C.20 D.26
9.如图在 ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AB到CD的距离与AD到BC的距离相等
10. 在 ABCD中,AB=4,BC=6,若∠B=45°,则 ABCD的面积为( )
A.8 B.12 C.16 D.24
11.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6, ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
12.如图,在 ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为E,F,G,H,则图中面积相等的平行四边形的对数为( )
A.1 B.2 C.3 D.4
二.题空题(每小题3分 共30分)
13.如图剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是____.
第13题图 第14题图 第15题图 第16题图 第17题图
13.如图, ABCD的周长为18 cm,AE平分∠BAD,若CE=1 cm,则AB的长度是____cm.
14.在 ABCD中,AB=3 cm,BC=5 cm,∠A=30°,则CD=__3__cm__,AD=__5 cm__,∠B=____,∠C=____,∠D=____.
15.如图,方格纸中每个最小正方形的边长为1,则两平行直线AB,CD之间的距离是____.
16.如图,AD∥BC,AC,BD交于点E,三角形ABE的面积等于2,三角形CBE的面积等于3,那么三角形DBC的面积等于____.
17.如图, ABCD的对角线AC,BD相交于点O,且AB=12,AC=10,BD=26,则 ABCD的面积为____.
18.如图,已知 ABCD的对角线AC,BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2,则AB的长为____,BC的长为____.
第18题图 第19题图 第20题图 第22题图
19.如图,在 ABCD中,∠C=43°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为____.
20.如图,在 ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以点M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线AP交边CD于点Q.若DQ=2QC,BC=3,则 ABCD的周长为____.
21.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=____.
22.如图,在 ABCD中,AE,AF分别垂直于BC,CD,垂足为E,F,若∠EAF=30°,AB=6,AD=10,则CD=__6__;AB与CD的距离为____;AD与BC的距离为____;∠D=____.
三.解答题(54分)
23.(5分)如图,在平行四边形ABCD中,M,N分别是AD,BC上的点,过点M作EM⊥AB,交AB的延长线于点E,过点N作FN⊥DC,交DC的延长线于点F,且EM=FN,
求证:AM=CN.
24.(6分)如图①, ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F,则OE=OF.若将EF向两方延长与平行四边形的两对边的延长线分别相交(图②和图③),OE与OF还相等吗?若相等,请说明你的理由.
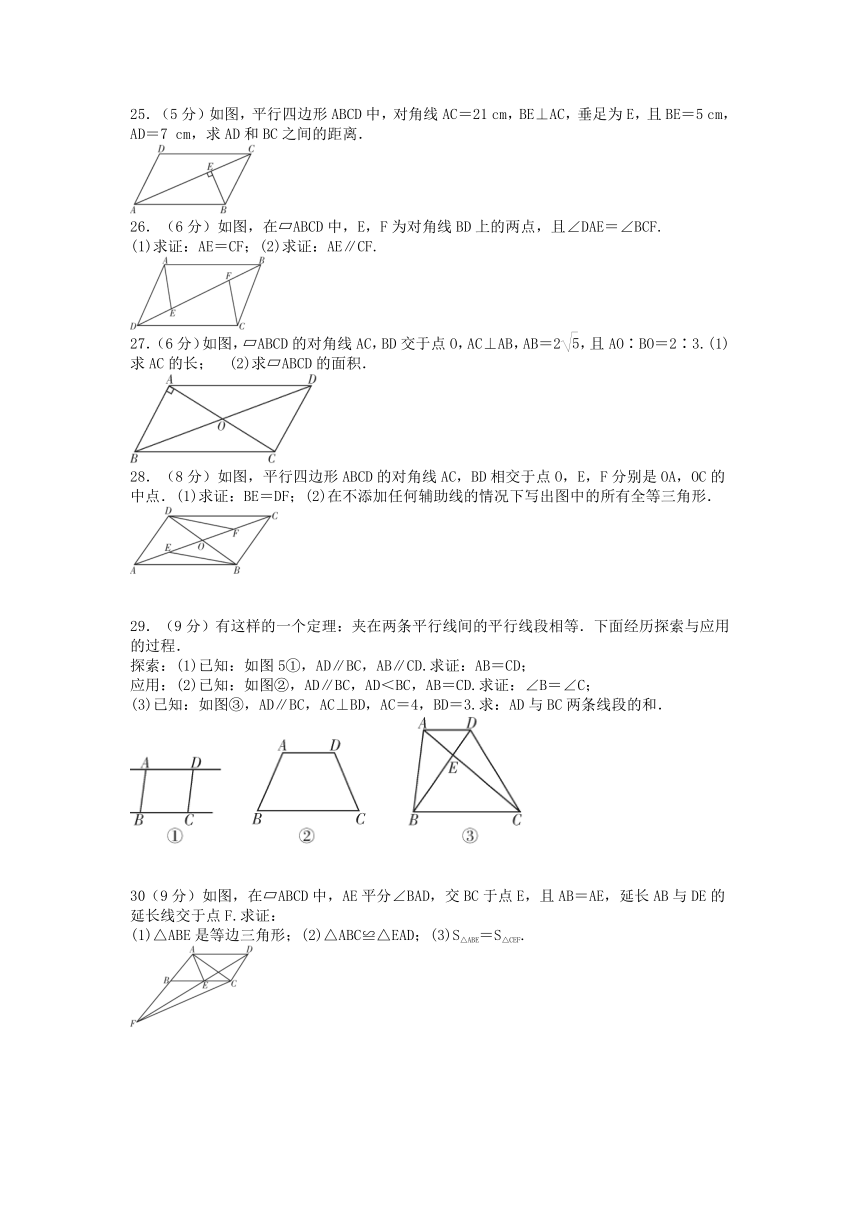
25.(5分)如图,平行四边形ABCD中,对角线AC=21 cm,BE⊥AC,垂足为E,且BE=5 cm,AD=7 cm,求AD和BC之间的距离.
26.(6分)如图,在 ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.
(1)求证:AE=CF;(2)求证:AE∥CF.
27.(6分)如图, ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.(1)求AC的长; (2)求 ABCD的面积.
28.(8分)如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.(1)求证:BE=DF;(2)在不添加任何辅助线的情况下写出图中的所有全等三角形.
29.(9分)有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:(1)已知:如图5①,AD∥BC,AB∥CD.求证:AB=CD;
应用:(2)已知:如图②,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;
(3)已知:如图③,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
30(9分)如图,在 ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.求证:
(1)△ABE是等边三角形;(2)△ABC≌△EAD;(3)S△ABE=S△CEF.
教师样卷
一.选择题(每小题3分 共36分)
1.平行四边形不一定具有的特征是( B )
A.内角和为360度 B.对角互补 C.邻角互补 D.对角相等
2.如图,在 ABCD中,AC=4 cm.若△ACD的周长是12 cm,则平行四边形ABCD的周长是( A )
A.16 cm B.18 cm C.20 cm D.24 cm
【解析】 ∵AC=4 cm,△ADC的周长为12 cm,∴AD+DC=12-4=8(cm).又∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∴平行四边形的周长为2(AD+DC)=16 cm.
第2题图 第3题图 第4题图 第5题图 第6题图
3.如图3,在 ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( C )
A.1 B. C.2 D.3
【解析】 ∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC=5,AB=CD=3,∴∠ABE=∠CFE,∵∠ABC的平分线交AD于点E,∴∠ABE=∠CBF,∴∠CBF=∠CFB,∴CF=CB=5,∴DF=CF-CD=5-3=2.
4.如图,在平行四边形ABCD中,点E在边AB上,点F在边CD上,如果添加一个条件,使△ADE≌△CBF,那么添加的条件不能为( A )
A.DE=BF B.AE=CF C.BE=DF D.∠ADE=∠CBF
【解析】 ∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C.当DE=BF时,不能用SSA证明△ADE≌△CBF,所以A选项内容错误,符合题意;当AE=CF时,用SAS可以证明△ADE≌△CBF,所以B选项内容正确,不符合题意;当BE=DF时,则AB-BE=CD-DF,即AE=CF,与B答案思路一样,所以C选项内容正确,不符合题意;当∠ADE=∠CBF时,用ASA可以证明△ADE≌△CBF,所以D选项内容正确,不符合题意
5.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3 cm,直线b与c之间的距离是5 cm,那么直线a与c的距离是( C )
A.2 cm B.8 cm C.8或2 cm D.不能确定
【解析】 (1)如答图①,直线a与c的距离是3 cm+5 cm=8 cm;(2)如答图②,直线a与c的距离是5 cm-3 cm=2 cm.
5.如图3,直线l1∥l2,△ABC的面积为10,则△DBC的面积( C )
A.大于10 B.小于10 C.等于10 D.无法确定
【解析】 ∵l1∥l2,∴l1,l2之间的距离是固定的,∴△ABC和△DBC的BC边上的高相等,∴△ABC和△DBC的面积相等,∴△DBC的面积等于10.
6.如图所示,l1∥l2,AB∥CD,CE⊥l1,FG⊥l2,E,G为垂足,则下列说法中错误的是(D )
A.CD>CE B.A,B两点间的距离就是线段AB的长
C.CE=FG D.l1,l2间的距离就是线段CD的长
【解析】 A.∵l1∥l2,CE⊥l1,∴CD>CE,故本选项说法正确;B.∵AB是线段,∴A,B两点间距离就是线段AB的长度,故本选项说法正确;C.∵l1∥l2,CE⊥l1,FG⊥l2,∴CE=FG,故本选项说法正确;D.∵CE⊥l2于点E,∴l1与l2两平行线间的距离就是线段CE的长度,故本选项说法错误.
7.如图,在 ABCD中,O是对角线AC,BD的交点,下列结论错误的是( C )
A.AB∥CD B.AB=CD C.AC=BD D.OA=OC
第7题图 第8题图 第9题图 第10题图 第11题图 第12题图
8.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( B )
A.13 B.17 C.20 D.26
9.如图在 ABCD中,下列结论中错误的是( D )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AB到CD的距离与AD到BC的距离相等
10. 在 ABCD中,AB=4,BC=6,若∠B=45°,则 ABCD的面积为( B )
A.8 B.12 C.16 D.24
【解析】 如答图,过点A作AE⊥BC于点E.∵∠B=45°,∴∠BAE=45°,∴BE=AE.设AE=x,则BE=x,∵AB2=BE2+AE2,∴2x2=42,解得x=2,∴S ABCD=BC·AE=6×2=12.故选B.
11.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6, ABCD的周长为40,则 ABCD的面积为( D )
A.24 B.36 C.40 D.48
【解析】 设BC=x,则CD=20-x,根据“等面积法”,得4x=6(20-x),解得x=12,∴S ABCD=4x=4×12=48.故选D.
12.如图,在 ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为E,F,G,H,则图中面积相等的平行四边形的对数为( C )
A.1 B.2 C.3 D.4
【解析】 ∵四边形ABCD为平行四边形,BD为对角线,∴S△ABD=S△BCD,同理,S△BFP=S△BGP,S△PED=S△HPD,∵S△BCD-S△BFP-S△PHD=S PFCH,S△ABD-S△BGP-S△EPD=S AGPE.∴S PFCH=S AGPE,∴S PFCH+S PHDE=S AGPE+S PHDE,S PFCH+S BFPG=S AGPE+S BFPG,∴S AGHD=S EFCD,S ABFE=S BCHG.共有3对面积相等的平行四边形,故选C.
二.题空题(每小题3分 共30分)
13.如图剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是__平行四边形__.
【解析】 由条件可知AB∥CD,AD∥BC,∴四边形ABCD为平行四边形.
第13题图 第14题图 第15题图 第16题图 第17题图
13.如图, ABCD的周长为18 cm,AE平分∠BAD,若CE=1 cm,则AB的长度是__4__cm.
【解析】 ∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,AD∥BC,∴∠DAE=∠BEA,∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠AEB,∴AB=BE,设AB=CD=x cm,则AD=BC=(x+1)cm,∵ ABCD的周长为18 cm,∴x+x+1=9,解得x=4,即AB=4 cm.
14.在 ABCD中,AB=3 cm,BC=5 cm,∠A=30°,则CD=__3__cm__,AD=__5 cm__,∠B=__150°__,∠C=__30°__,∠D=__150°__.
15.如图,方格纸中每个最小正方形的边长为1,则两平行直线AB,CD之间的距离是__3__.
16.如图,AD∥BC,AC,BD交于点E,三角形ABE的面积等于2,三角形CBE的面积等于3,那么三角形DBC的面积等于__5__.
【解析】 ∵AD∥BC,∴S△ABD=S△ACD,∴S△ABE=S△ECD=2,∴S△DBC=S△ECD+S△BCE=2+3=5.
17.如图, ABCD的对角线AC,BD相交于点O,且AB=12,AC=10,BD=26,则 ABCD的面积为__120__.
【解析】 ∵四边形ABCD是平行四边形,∴OA=AC=5,OB=BD=13,∵AB=12,∴OA2+AB2=OB2,∴AC⊥AB,∴∠BAC=90°,∴ ABCD的面积=AB·AC=12×10=120.
18.如图,已知 ABCD的对角线AC,BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2,则AB的长为__3__,BC的长为__5__.
【解析】 ∵ ABCD的对角线AC,BD相交于点O,其周长为16,∴OA=OC,OB=OD,AB=CD,AD=CB,∴BC+AB=8①,∵△AOB的周长比△BOC的周长小2,∴OB+OC+BC-(OA+OB+AB)=2,∴BC-AB=2②,①+②,得2BC=10,∴BC=5,∴AB=3.
第18题图 第19题图 第20题图 第22题图
19.如图,在 ABCD中,∠C=43°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为__47°__.
【解析】 ∵四边形ABCD是平行四边形,∴∠A=∠C=43°.∵DF⊥AD,∴∠ADE=90°,∴∠AED=90°-43°=47°,∴∠BEF=∠AED=47°.
20.如图,在 ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以点M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线AP交边CD于点Q.若DQ=2QC,BC=3,则 ABCD的周长为__15__.
【解析】 由作图知,AQ是∠BAD的平分线.∴∠DAQ=∠BAQ,又∵AB∥CD,∴∠DQA=∠BAQ,∴∠DQA=∠DAQ,∴DA=QD.∵DQ=2QC,BC=3,∴DQ=3,QC=1.5,∴ ABCD的周长为2(BC+CD)=2×7.5=15.
21.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=__4或-2__.
22.如图,在 ABCD中,AE,AF分别垂直于BC,CD,垂足为E,F,若∠EAF=30°,AB=6,AD=10,则CD=__6__;AB与CD的距离为__5__;AD与BC的距离为__3__;∠D=__30°__.
【解析】 ∵四边形ABCD是平行四边形,∴AB=CD=6,AD∥BC,AB∥DC,∵AE,AF分别垂直于BC,CD,垂足为E,F,∴AB与CD的距离为AF,AD与BC的距离为AE,∵∠EAF=30°,∴∠BCD=150°,∴∠B=∠D=30°,∵AB=6,∴AE=AB=3,∵AD=10,∴AF=AD=5.
三.解答题(54分)
23.(5分)如图,在平行四边形ABCD中,M,N分别是AD,BC上的点,过点M作EM⊥AB,交AB的延长线于点E,过点N作FN⊥DC,交DC的延长线于点F,且EM=FN,
求证:AM=CN.
证明:∵四边形ABCD是平行四边形,∴∠BAD=∠BCD,∴∠EAM=∠FCN,∵EM⊥BE,FN⊥DF,∴∠E=∠F,在△EAM和△FCN中,∴△EAM≌△FCN(AAS),∴AM=CN.
24.(6分)如图①, ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F,则OE=OF.若将EF向两方延长与平行四边形的两对边的延长线分别相交(图②和图③),OE与OF还相等吗?若相等,请说明你的理由.
解:图②中仍然相等.∵在 ABCD中,AB∥CD,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,
∴△AOE≌△COF(AAS).∴OE=OF;图③中仍然相等.∵在 ABCD中,AD∥BC,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌△COF(AAS).∴OE=OF.
25.(5分)如图,平行四边形ABCD中,对角线AC=21 cm,BE⊥AC,垂足为E,且BE=5 cm,AD=7 cm,求AD和BC之间的距离.
解:设AD和BC之间的距离为x,则平行四边形ABCD的面积等于AD·x,∵S平行四边行ABCD=2S△ABC=2×AC·BE=AC·BE,∴AD·x=AC·BE,即7x=21×5,解得x=15.
答:AD和BC之间的距离为15 cm.
26.(6分)如图,在 ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.
(1)求证:AE=CF;(2)求证:AE∥CF.
证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
在△DAE和△BCF中,∴△DAE≌△BCF(ASA),∴AE=CF;
(2)∵△DAE≌△BCF,∴∠AED=∠CFB,∴∠AEB=∠CFD,∴AE∥CF.
27.(6分)如图, ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.(1)求AC的长; (2)求 ABCD的面积.
解:(1)∵OA∶OB=2∶3,∴设OA=2x,OB=3x.∵AC⊥AB,AB=2,∴(2x)2+(2)2=(3x)2.解得x=2(负值舍去).∴OA=4.∵四边形ABCD是平行四边形,∴AC=2AO=8;
(2)∵S△ABC=AB·AC=×2×8=8,∴S ABCD=2S△ABC=2×8=16.
28.(8分)如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.(1)求证:BE=DF;(2)在不添加任何辅助线的情况下写出图中的所有全等三角形.
解:(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,OA=OC,OB=OD,AB∥CD,∴∠BAE=∠DCF,∵E,F分别是OA,OC的中点,
∴AE=OE=OA,CF=OF=OC,∴AE=CF,
在△ABE和△CDF中,∴△ABE≌△CDF(SAS),∴BE=DF;
(2)图中的所有全等三角形为△AOD≌△COB,△AOB≌△COD,△ABC≌△CDA,△ABD≌△CDB,△ABE≌△CDF,△BOE≌△DOF,理由如下:∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,OA=OC,OB=OD,在△AOD和△COB中,
∴△AOD≌△COB(SAS),同理△AOB≌△COD,在△ABC和△CDA中,
∴△ABC≌△CDA(SSS),同理:△ABD≌△CDB,由(1),得△ABE≌△CDF;在△BOE和△DOF中,∴△BOE≌△DOF(SAS).
29.(9分)有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:(1)已知:如图5①,AD∥BC,AB∥CD.求证:AB=CD;
应用:(2)已知:如图②,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;
(3)已知:如图③,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
解:(1)证明:如答图①,连结AC,∵AD∥BC,∴∠DAC=∠BCA,∵AB∥CD.∴∠BAC=∠DCA,在△ABC和△CDA中,∴△ABC≌△CDA(ASA),∴AB=CD;
(2)证明:如答图②,作DE∥AB交BC于点E,∵AD∥BC,∴AB=DE,∵AB=CD,∴DE=CD,∴∠DEC=∠C,∵DE∥AB,∴∠B=∠DEC,∴∠B=∠C;
(3)如答图③,作DF∥AC交BC的延长线于点F,∵AD∥BC,∴AC=DF,AD=CF,∵AC⊥BD,∴∠BDF=∠BEC=90°,在Rt△BDF中,由勾股定理得BF=5,故BC+AD=BC+CF=BF=5.
30(9分)如图,在 ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.求证:
(1)△ABE是等边三角形;(2)△ABC≌△EAD;(3)S△ABE=S△CEF.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAD=∠AEB,又∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠BEA,∴AB=BE,∵AB=AE,∴△ABE是等边三角形.
(2)∵△ABE是等边三角形∴∠ABE=∠EAD=60°,∵AB=AE,BC=AD,∴△ABC≌△EAD(SAS);
(3)∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),∴S△FCD=S△ABC,又∵△AEC与△DEC同底等高,∴S△AEC=S△DEC,∴S△ABC-S△AEC=S△FCD-SDEC,∴S△ABE=S△CEF.
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共36分)
1.平行四边形不一定具有的特征是( )
A.内角和为360度 B.对角互补 C.邻角互补 D.对角相等
2.如图,在 ABCD中,AC=4 cm.若△ACD的周长是12 cm,则平行四边形ABCD的周长是( )
A.16 cm B.18 cm C.20 cm D.24 cm
第2题图 第3题图 第4题图 第5题图 第6题图
3.如图3,在 ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.1 B. C.2 D.3
4.如图,在平行四边形ABCD中,点E在边AB上,点F在边CD上,如果添加一个条件,使△ADE≌△CBF,那么添加的条件不能为( )
A.DE=BF B.AE=CF C.BE=DF D.∠ADE=∠CBF
5.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3 cm,直线b与c之间的距离是5 cm,那么直线a与c的距离是( )
A.2 cm B.8 cm C.8或2 cm D.不能确定
5.如图3,直线l1∥l2,△ABC的面积为10,则△DBC的面积( )
A.大于10 B.小于10 C.等于10 D.无法确定
6.如图所示,l1∥l2,AB∥CD,CE⊥l1,FG⊥l2,E,G为垂足,则下列说法中错误的是( )
A.CD>CE B.A,B两点间的距离就是线段AB的长
C.CE=FG D.l1,l2间的距离就是线段CD的长
7.如图,在 ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )
A.AB∥CD B.AB=CD C.AC=BD D.OA=OC
第7题图 第8题图 第9题图 第10题图 第11题图 第12题图
8.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13 B.17 C.20 D.26
9.如图在 ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AB到CD的距离与AD到BC的距离相等
10. 在 ABCD中,AB=4,BC=6,若∠B=45°,则 ABCD的面积为( )
A.8 B.12 C.16 D.24
11.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6, ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
12.如图,在 ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为E,F,G,H,则图中面积相等的平行四边形的对数为( )
A.1 B.2 C.3 D.4
二.题空题(每小题3分 共30分)
13.如图剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是____.
第13题图 第14题图 第15题图 第16题图 第17题图
13.如图, ABCD的周长为18 cm,AE平分∠BAD,若CE=1 cm,则AB的长度是____cm.
14.在 ABCD中,AB=3 cm,BC=5 cm,∠A=30°,则CD=__3__cm__,AD=__5 cm__,∠B=____,∠C=____,∠D=____.
15.如图,方格纸中每个最小正方形的边长为1,则两平行直线AB,CD之间的距离是____.
16.如图,AD∥BC,AC,BD交于点E,三角形ABE的面积等于2,三角形CBE的面积等于3,那么三角形DBC的面积等于____.
17.如图, ABCD的对角线AC,BD相交于点O,且AB=12,AC=10,BD=26,则 ABCD的面积为____.
18.如图,已知 ABCD的对角线AC,BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2,则AB的长为____,BC的长为____.
第18题图 第19题图 第20题图 第22题图
19.如图,在 ABCD中,∠C=43°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为____.
20.如图,在 ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以点M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线AP交边CD于点Q.若DQ=2QC,BC=3,则 ABCD的周长为____.
21.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=____.
22.如图,在 ABCD中,AE,AF分别垂直于BC,CD,垂足为E,F,若∠EAF=30°,AB=6,AD=10,则CD=__6__;AB与CD的距离为____;AD与BC的距离为____;∠D=____.
三.解答题(54分)
23.(5分)如图,在平行四边形ABCD中,M,N分别是AD,BC上的点,过点M作EM⊥AB,交AB的延长线于点E,过点N作FN⊥DC,交DC的延长线于点F,且EM=FN,
求证:AM=CN.
24.(6分)如图①, ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F,则OE=OF.若将EF向两方延长与平行四边形的两对边的延长线分别相交(图②和图③),OE与OF还相等吗?若相等,请说明你的理由.
25.(5分)如图,平行四边形ABCD中,对角线AC=21 cm,BE⊥AC,垂足为E,且BE=5 cm,AD=7 cm,求AD和BC之间的距离.
26.(6分)如图,在 ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.
(1)求证:AE=CF;(2)求证:AE∥CF.
27.(6分)如图, ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.(1)求AC的长; (2)求 ABCD的面积.
28.(8分)如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.(1)求证:BE=DF;(2)在不添加任何辅助线的情况下写出图中的所有全等三角形.
29.(9分)有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:(1)已知:如图5①,AD∥BC,AB∥CD.求证:AB=CD;
应用:(2)已知:如图②,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;
(3)已知:如图③,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
30(9分)如图,在 ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.求证:
(1)△ABE是等边三角形;(2)△ABC≌△EAD;(3)S△ABE=S△CEF.
教师样卷
一.选择题(每小题3分 共36分)
1.平行四边形不一定具有的特征是( B )
A.内角和为360度 B.对角互补 C.邻角互补 D.对角相等
2.如图,在 ABCD中,AC=4 cm.若△ACD的周长是12 cm,则平行四边形ABCD的周长是( A )
A.16 cm B.18 cm C.20 cm D.24 cm
【解析】 ∵AC=4 cm,△ADC的周长为12 cm,∴AD+DC=12-4=8(cm).又∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∴平行四边形的周长为2(AD+DC)=16 cm.
第2题图 第3题图 第4题图 第5题图 第6题图
3.如图3,在 ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( C )
A.1 B. C.2 D.3
【解析】 ∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC=5,AB=CD=3,∴∠ABE=∠CFE,∵∠ABC的平分线交AD于点E,∴∠ABE=∠CBF,∴∠CBF=∠CFB,∴CF=CB=5,∴DF=CF-CD=5-3=2.
4.如图,在平行四边形ABCD中,点E在边AB上,点F在边CD上,如果添加一个条件,使△ADE≌△CBF,那么添加的条件不能为( A )
A.DE=BF B.AE=CF C.BE=DF D.∠ADE=∠CBF
【解析】 ∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C.当DE=BF时,不能用SSA证明△ADE≌△CBF,所以A选项内容错误,符合题意;当AE=CF时,用SAS可以证明△ADE≌△CBF,所以B选项内容正确,不符合题意;当BE=DF时,则AB-BE=CD-DF,即AE=CF,与B答案思路一样,所以C选项内容正确,不符合题意;当∠ADE=∠CBF时,用ASA可以证明△ADE≌△CBF,所以D选项内容正确,不符合题意
5.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3 cm,直线b与c之间的距离是5 cm,那么直线a与c的距离是( C )
A.2 cm B.8 cm C.8或2 cm D.不能确定
【解析】 (1)如答图①,直线a与c的距离是3 cm+5 cm=8 cm;(2)如答图②,直线a与c的距离是5 cm-3 cm=2 cm.
5.如图3,直线l1∥l2,△ABC的面积为10,则△DBC的面积( C )
A.大于10 B.小于10 C.等于10 D.无法确定
【解析】 ∵l1∥l2,∴l1,l2之间的距离是固定的,∴△ABC和△DBC的BC边上的高相等,∴△ABC和△DBC的面积相等,∴△DBC的面积等于10.
6.如图所示,l1∥l2,AB∥CD,CE⊥l1,FG⊥l2,E,G为垂足,则下列说法中错误的是(D )
A.CD>CE B.A,B两点间的距离就是线段AB的长
C.CE=FG D.l1,l2间的距离就是线段CD的长
【解析】 A.∵l1∥l2,CE⊥l1,∴CD>CE,故本选项说法正确;B.∵AB是线段,∴A,B两点间距离就是线段AB的长度,故本选项说法正确;C.∵l1∥l2,CE⊥l1,FG⊥l2,∴CE=FG,故本选项说法正确;D.∵CE⊥l2于点E,∴l1与l2两平行线间的距离就是线段CE的长度,故本选项说法错误.
7.如图,在 ABCD中,O是对角线AC,BD的交点,下列结论错误的是( C )
A.AB∥CD B.AB=CD C.AC=BD D.OA=OC
第7题图 第8题图 第9题图 第10题图 第11题图 第12题图
8.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( B )
A.13 B.17 C.20 D.26
9.如图在 ABCD中,下列结论中错误的是( D )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AB到CD的距离与AD到BC的距离相等
10. 在 ABCD中,AB=4,BC=6,若∠B=45°,则 ABCD的面积为( B )
A.8 B.12 C.16 D.24
【解析】 如答图,过点A作AE⊥BC于点E.∵∠B=45°,∴∠BAE=45°,∴BE=AE.设AE=x,则BE=x,∵AB2=BE2+AE2,∴2x2=42,解得x=2,∴S ABCD=BC·AE=6×2=12.故选B.
11.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6, ABCD的周长为40,则 ABCD的面积为( D )
A.24 B.36 C.40 D.48
【解析】 设BC=x,则CD=20-x,根据“等面积法”,得4x=6(20-x),解得x=12,∴S ABCD=4x=4×12=48.故选D.
12.如图,在 ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为E,F,G,H,则图中面积相等的平行四边形的对数为( C )
A.1 B.2 C.3 D.4
【解析】 ∵四边形ABCD为平行四边形,BD为对角线,∴S△ABD=S△BCD,同理,S△BFP=S△BGP,S△PED=S△HPD,∵S△BCD-S△BFP-S△PHD=S PFCH,S△ABD-S△BGP-S△EPD=S AGPE.∴S PFCH=S AGPE,∴S PFCH+S PHDE=S AGPE+S PHDE,S PFCH+S BFPG=S AGPE+S BFPG,∴S AGHD=S EFCD,S ABFE=S BCHG.共有3对面积相等的平行四边形,故选C.
二.题空题(每小题3分 共30分)
13.如图剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是__平行四边形__.
【解析】 由条件可知AB∥CD,AD∥BC,∴四边形ABCD为平行四边形.
第13题图 第14题图 第15题图 第16题图 第17题图
13.如图, ABCD的周长为18 cm,AE平分∠BAD,若CE=1 cm,则AB的长度是__4__cm.
【解析】 ∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,AD∥BC,∴∠DAE=∠BEA,∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠AEB,∴AB=BE,设AB=CD=x cm,则AD=BC=(x+1)cm,∵ ABCD的周长为18 cm,∴x+x+1=9,解得x=4,即AB=4 cm.
14.在 ABCD中,AB=3 cm,BC=5 cm,∠A=30°,则CD=__3__cm__,AD=__5 cm__,∠B=__150°__,∠C=__30°__,∠D=__150°__.
15.如图,方格纸中每个最小正方形的边长为1,则两平行直线AB,CD之间的距离是__3__.
16.如图,AD∥BC,AC,BD交于点E,三角形ABE的面积等于2,三角形CBE的面积等于3,那么三角形DBC的面积等于__5__.
【解析】 ∵AD∥BC,∴S△ABD=S△ACD,∴S△ABE=S△ECD=2,∴S△DBC=S△ECD+S△BCE=2+3=5.
17.如图, ABCD的对角线AC,BD相交于点O,且AB=12,AC=10,BD=26,则 ABCD的面积为__120__.
【解析】 ∵四边形ABCD是平行四边形,∴OA=AC=5,OB=BD=13,∵AB=12,∴OA2+AB2=OB2,∴AC⊥AB,∴∠BAC=90°,∴ ABCD的面积=AB·AC=12×10=120.
18.如图,已知 ABCD的对角线AC,BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2,则AB的长为__3__,BC的长为__5__.
【解析】 ∵ ABCD的对角线AC,BD相交于点O,其周长为16,∴OA=OC,OB=OD,AB=CD,AD=CB,∴BC+AB=8①,∵△AOB的周长比△BOC的周长小2,∴OB+OC+BC-(OA+OB+AB)=2,∴BC-AB=2②,①+②,得2BC=10,∴BC=5,∴AB=3.
第18题图 第19题图 第20题图 第22题图
19.如图,在 ABCD中,∠C=43°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为__47°__.
【解析】 ∵四边形ABCD是平行四边形,∴∠A=∠C=43°.∵DF⊥AD,∴∠ADE=90°,∴∠AED=90°-43°=47°,∴∠BEF=∠AED=47°.
20.如图,在 ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以点M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线AP交边CD于点Q.若DQ=2QC,BC=3,则 ABCD的周长为__15__.
【解析】 由作图知,AQ是∠BAD的平分线.∴∠DAQ=∠BAQ,又∵AB∥CD,∴∠DQA=∠BAQ,∴∠DQA=∠DAQ,∴DA=QD.∵DQ=2QC,BC=3,∴DQ=3,QC=1.5,∴ ABCD的周长为2(BC+CD)=2×7.5=15.
21.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=__4或-2__.
22.如图,在 ABCD中,AE,AF分别垂直于BC,CD,垂足为E,F,若∠EAF=30°,AB=6,AD=10,则CD=__6__;AB与CD的距离为__5__;AD与BC的距离为__3__;∠D=__30°__.
【解析】 ∵四边形ABCD是平行四边形,∴AB=CD=6,AD∥BC,AB∥DC,∵AE,AF分别垂直于BC,CD,垂足为E,F,∴AB与CD的距离为AF,AD与BC的距离为AE,∵∠EAF=30°,∴∠BCD=150°,∴∠B=∠D=30°,∵AB=6,∴AE=AB=3,∵AD=10,∴AF=AD=5.
三.解答题(54分)
23.(5分)如图,在平行四边形ABCD中,M,N分别是AD,BC上的点,过点M作EM⊥AB,交AB的延长线于点E,过点N作FN⊥DC,交DC的延长线于点F,且EM=FN,
求证:AM=CN.
证明:∵四边形ABCD是平行四边形,∴∠BAD=∠BCD,∴∠EAM=∠FCN,∵EM⊥BE,FN⊥DF,∴∠E=∠F,在△EAM和△FCN中,∴△EAM≌△FCN(AAS),∴AM=CN.
24.(6分)如图①, ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F,则OE=OF.若将EF向两方延长与平行四边形的两对边的延长线分别相交(图②和图③),OE与OF还相等吗?若相等,请说明你的理由.
解:图②中仍然相等.∵在 ABCD中,AB∥CD,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,
∴△AOE≌△COF(AAS).∴OE=OF;图③中仍然相等.∵在 ABCD中,AD∥BC,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌△COF(AAS).∴OE=OF.
25.(5分)如图,平行四边形ABCD中,对角线AC=21 cm,BE⊥AC,垂足为E,且BE=5 cm,AD=7 cm,求AD和BC之间的距离.
解:设AD和BC之间的距离为x,则平行四边形ABCD的面积等于AD·x,∵S平行四边行ABCD=2S△ABC=2×AC·BE=AC·BE,∴AD·x=AC·BE,即7x=21×5,解得x=15.
答:AD和BC之间的距离为15 cm.
26.(6分)如图,在 ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.
(1)求证:AE=CF;(2)求证:AE∥CF.
证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
在△DAE和△BCF中,∴△DAE≌△BCF(ASA),∴AE=CF;
(2)∵△DAE≌△BCF,∴∠AED=∠CFB,∴∠AEB=∠CFD,∴AE∥CF.
27.(6分)如图, ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.(1)求AC的长; (2)求 ABCD的面积.
解:(1)∵OA∶OB=2∶3,∴设OA=2x,OB=3x.∵AC⊥AB,AB=2,∴(2x)2+(2)2=(3x)2.解得x=2(负值舍去).∴OA=4.∵四边形ABCD是平行四边形,∴AC=2AO=8;
(2)∵S△ABC=AB·AC=×2×8=8,∴S ABCD=2S△ABC=2×8=16.
28.(8分)如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.(1)求证:BE=DF;(2)在不添加任何辅助线的情况下写出图中的所有全等三角形.
解:(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,OA=OC,OB=OD,AB∥CD,∴∠BAE=∠DCF,∵E,F分别是OA,OC的中点,
∴AE=OE=OA,CF=OF=OC,∴AE=CF,
在△ABE和△CDF中,∴△ABE≌△CDF(SAS),∴BE=DF;
(2)图中的所有全等三角形为△AOD≌△COB,△AOB≌△COD,△ABC≌△CDA,△ABD≌△CDB,△ABE≌△CDF,△BOE≌△DOF,理由如下:∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,OA=OC,OB=OD,在△AOD和△COB中,
∴△AOD≌△COB(SAS),同理△AOB≌△COD,在△ABC和△CDA中,
∴△ABC≌△CDA(SSS),同理:△ABD≌△CDB,由(1),得△ABE≌△CDF;在△BOE和△DOF中,∴△BOE≌△DOF(SAS).
29.(9分)有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:(1)已知:如图5①,AD∥BC,AB∥CD.求证:AB=CD;
应用:(2)已知:如图②,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;
(3)已知:如图③,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
解:(1)证明:如答图①,连结AC,∵AD∥BC,∴∠DAC=∠BCA,∵AB∥CD.∴∠BAC=∠DCA,在△ABC和△CDA中,∴△ABC≌△CDA(ASA),∴AB=CD;
(2)证明:如答图②,作DE∥AB交BC于点E,∵AD∥BC,∴AB=DE,∵AB=CD,∴DE=CD,∴∠DEC=∠C,∵DE∥AB,∴∠B=∠DEC,∴∠B=∠C;
(3)如答图③,作DF∥AC交BC的延长线于点F,∵AD∥BC,∴AC=DF,AD=CF,∵AC⊥BD,∴∠BDF=∠BEC=90°,在Rt△BDF中,由勾股定理得BF=5,故BC+AD=BC+CF=BF=5.
30(9分)如图,在 ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.求证:
(1)△ABE是等边三角形;(2)△ABC≌△EAD;(3)S△ABE=S△CEF.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAD=∠AEB,又∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠BEA,∴AB=BE,∵AB=AE,∴△ABE是等边三角形.
(2)∵△ABE是等边三角形∴∠ABE=∠EAD=60°,∵AB=AE,BC=AD,∴△ABC≌△EAD(SAS);
(3)∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),∴S△FCD=S△ABC,又∵△AEC与△DEC同底等高,∴S△AEC=S△DEC,∴S△ABC-S△AEC=S△FCD-SDEC,∴S△ABE=S△CEF.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
