2021-2022学年人教版七年级数学下册5.3.1平行线的性质同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.3.1平行线的性质同步练习(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 345.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 22:21:54 | ||
图片预览

文档简介
5.3.1 平行线的性质
一、单项选择题
1. 如图,直线a,b被直线c所截.若a∥b,∠1=70°,则∠2的度数为( )
A.70° B.90° C.100° D.110°
2. 如图,DE∥BC,BE平分∠ABC.若∠1=66°,则∠CBE的度数为( )
A.22° B.32° C.33° D.56°
3. 如图,若a∥b,且∠2是∠1的2倍,则∠2的度数为( )
A.60° B.90° C.120° D.150°
4. 如图,将直角三角板ABC与直尺贴在一起,使三角板ABC的直角顶点C(∠ACB=90°)落在直尺的一边上.若∠2=25°,则∠1的度数为( )
A.60° B.65° C.70° D.75°
5. 一张两边平行的纸条,按如图所示的方式折叠,则∠1的度数为( )
A.30° B.40° C.50° D.60°
二、填空题
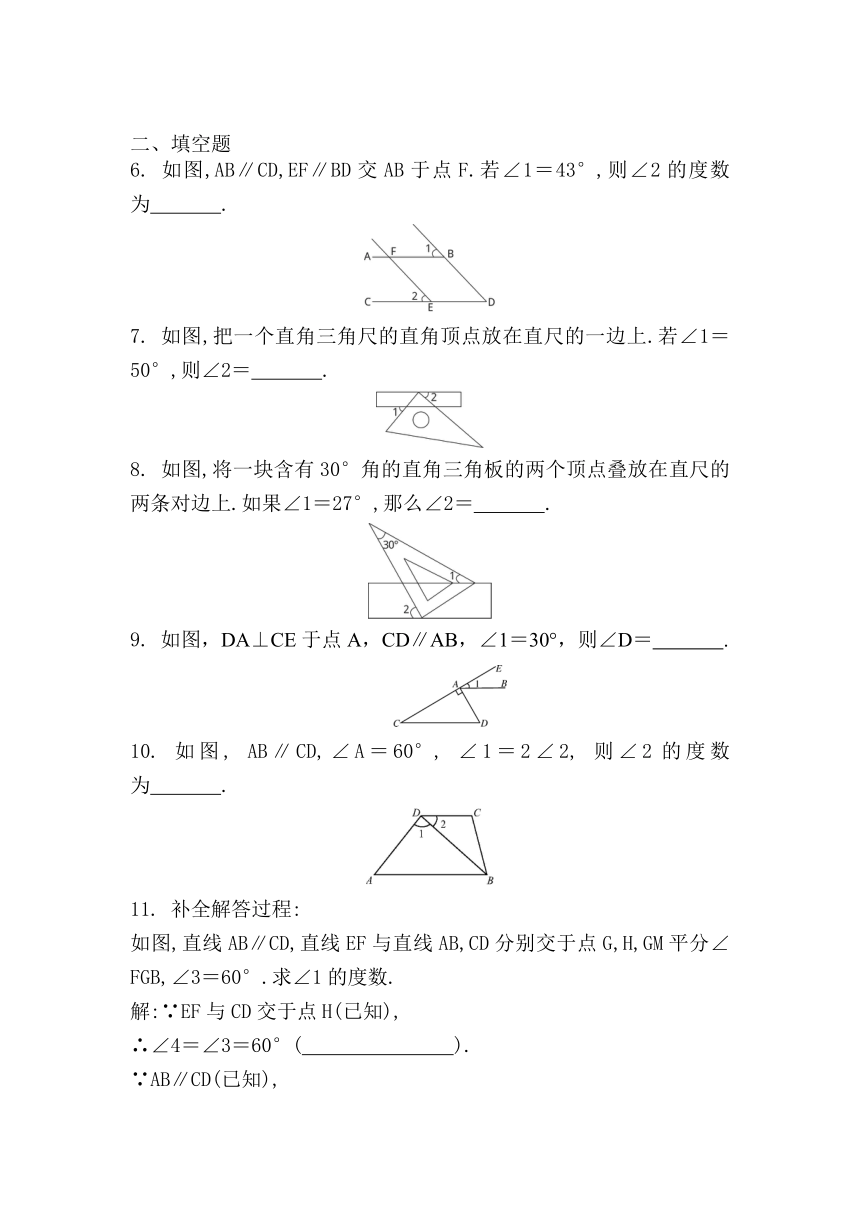
6. 如图,AB∥CD,EF∥BD交AB于点F.若∠1=43°,则∠2的度数为 .
7. 如图,把一个直角三角尺的直角顶点放在直尺的一边上.若∠1=50°,则∠2= .
8. 如图,将一块含有30°角的直角三角板的两个顶点叠放在直尺的两条对边上.如果∠1=27°,那么∠2= .
9. 如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
10. 如图, AB∥CD,∠A=60°, ∠1=2∠2, 则∠2的度数为 .
11. 补全解答过程:
如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H,GM平分∠FGB,∠3=60°.求∠1的度数.
解:∵EF与CD交于点H(已知),
∴∠4=∠3=60°( ).
∵AB∥CD(已知),
∴∠4+∠FGB=180°( ),
∴∠FGB= .
∵GM平分∠FGB(已知),
∴∠1= (角平分线的定义).
三、解答题
12. 如图,BC∥AD,BE∥AF.求证:∠A=∠B.
13. 如图,直线AB∥CD,直线l与AB,CD分别相交于点E,F,ED⊥EF交CD于点D,∠1=40°,求∠2的度数.
14.如图,AB∥CD.
(1)如图1,若∠CMN=90°,点B在射线MN上,∠ABM=120°,求∠C的度数;
(2)如图2,若∠CMN=150°,请直接写出∠ABM与∠C的数量关系.
15.如图,AB∥CD,EF∥MN,∠1=115°.
(1)求∠2和∠4的度数.
(2)本题隐含着一个规律,请你根据(1)中的结果进行归纳:如果一个角的两边分别平行于另一个角的两边,那么这两个角的关系如何
(3)利用(2)中的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的2倍少60°,求这两个角的度数.
答案:
一、
1-5 DCCBC
二、
6. 43°
7. 40°
8. 57°
9. 60°
10. 40°
11. 对顶角相等
两直线平行,同旁内角互补
120°
60°
三、
12. 证明:∵BC∥AD,∴∠B=∠DOE.
∵BE∥AF,∴∠DOE=∠A,∴∠A=∠B.
13. 解:∵ED⊥EF,∴∠1+∠BED=90°.
∵∠1=40°,∴∠BED=50°.
∵AB∥CD,∴∠2=∠BED=50°.
14. 解:(1)过点M作MK∥AB(点K在点M的左侧),
∴∠ABM+∠BMK=180°,
∴∠BMK=180°-∠ABM=60°.
∵∠CMN=90°,∴∠CMK=90°-∠BMK=30°.
∵AB∥CD,MK∥AB,∴MK∥CD,
∴∠C=∠CMK=30°.
(2)∠ABM-∠C=30°.
15. 解:(1)∵AB∥CD,∴∠2=∠1=115°.
又∵EF∥MN,∴∠4+∠2=180°,
∴∠4=180°-∠2=65°.
(2)由(1)可知,如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
(3)由(2)可知这两个角互补或相等,设一个角为x°,则另一个角为2x°-60°.
根据两个角互补,得x+2x-60=180,解得x=80,
∴这两个角分别为80°和100°.
根据两个角相等,得x=2x-60,解得x=60,
∴这两个角均为60°.
一、单项选择题
1. 如图,直线a,b被直线c所截.若a∥b,∠1=70°,则∠2的度数为( )
A.70° B.90° C.100° D.110°
2. 如图,DE∥BC,BE平分∠ABC.若∠1=66°,则∠CBE的度数为( )
A.22° B.32° C.33° D.56°
3. 如图,若a∥b,且∠2是∠1的2倍,则∠2的度数为( )
A.60° B.90° C.120° D.150°
4. 如图,将直角三角板ABC与直尺贴在一起,使三角板ABC的直角顶点C(∠ACB=90°)落在直尺的一边上.若∠2=25°,则∠1的度数为( )
A.60° B.65° C.70° D.75°
5. 一张两边平行的纸条,按如图所示的方式折叠,则∠1的度数为( )
A.30° B.40° C.50° D.60°
二、填空题
6. 如图,AB∥CD,EF∥BD交AB于点F.若∠1=43°,则∠2的度数为 .
7. 如图,把一个直角三角尺的直角顶点放在直尺的一边上.若∠1=50°,则∠2= .
8. 如图,将一块含有30°角的直角三角板的两个顶点叠放在直尺的两条对边上.如果∠1=27°,那么∠2= .
9. 如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
10. 如图, AB∥CD,∠A=60°, ∠1=2∠2, 则∠2的度数为 .
11. 补全解答过程:
如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H,GM平分∠FGB,∠3=60°.求∠1的度数.
解:∵EF与CD交于点H(已知),
∴∠4=∠3=60°( ).
∵AB∥CD(已知),
∴∠4+∠FGB=180°( ),
∴∠FGB= .
∵GM平分∠FGB(已知),
∴∠1= (角平分线的定义).
三、解答题
12. 如图,BC∥AD,BE∥AF.求证:∠A=∠B.
13. 如图,直线AB∥CD,直线l与AB,CD分别相交于点E,F,ED⊥EF交CD于点D,∠1=40°,求∠2的度数.
14.如图,AB∥CD.
(1)如图1,若∠CMN=90°,点B在射线MN上,∠ABM=120°,求∠C的度数;
(2)如图2,若∠CMN=150°,请直接写出∠ABM与∠C的数量关系.
15.如图,AB∥CD,EF∥MN,∠1=115°.
(1)求∠2和∠4的度数.
(2)本题隐含着一个规律,请你根据(1)中的结果进行归纳:如果一个角的两边分别平行于另一个角的两边,那么这两个角的关系如何
(3)利用(2)中的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的2倍少60°,求这两个角的度数.
答案:
一、
1-5 DCCBC
二、
6. 43°
7. 40°
8. 57°
9. 60°
10. 40°
11. 对顶角相等
两直线平行,同旁内角互补
120°
60°
三、
12. 证明:∵BC∥AD,∴∠B=∠DOE.
∵BE∥AF,∴∠DOE=∠A,∴∠A=∠B.
13. 解:∵ED⊥EF,∴∠1+∠BED=90°.
∵∠1=40°,∴∠BED=50°.
∵AB∥CD,∴∠2=∠BED=50°.
14. 解:(1)过点M作MK∥AB(点K在点M的左侧),
∴∠ABM+∠BMK=180°,
∴∠BMK=180°-∠ABM=60°.
∵∠CMN=90°,∴∠CMK=90°-∠BMK=30°.
∵AB∥CD,MK∥AB,∴MK∥CD,
∴∠C=∠CMK=30°.
(2)∠ABM-∠C=30°.
15. 解:(1)∵AB∥CD,∴∠2=∠1=115°.
又∵EF∥MN,∴∠4+∠2=180°,
∴∠4=180°-∠2=65°.
(2)由(1)可知,如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
(3)由(2)可知这两个角互补或相等,设一个角为x°,则另一个角为2x°-60°.
根据两个角互补,得x+2x-60=180,解得x=80,
∴这两个角分别为80°和100°.
根据两个角相等,得x=2x-60,解得x=60,
∴这两个角均为60°.
