2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质和判定第2课时矩形的判定基础练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质和判定第2课时矩形的判定基础练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 123.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 22:48:26 | ||
图片预览

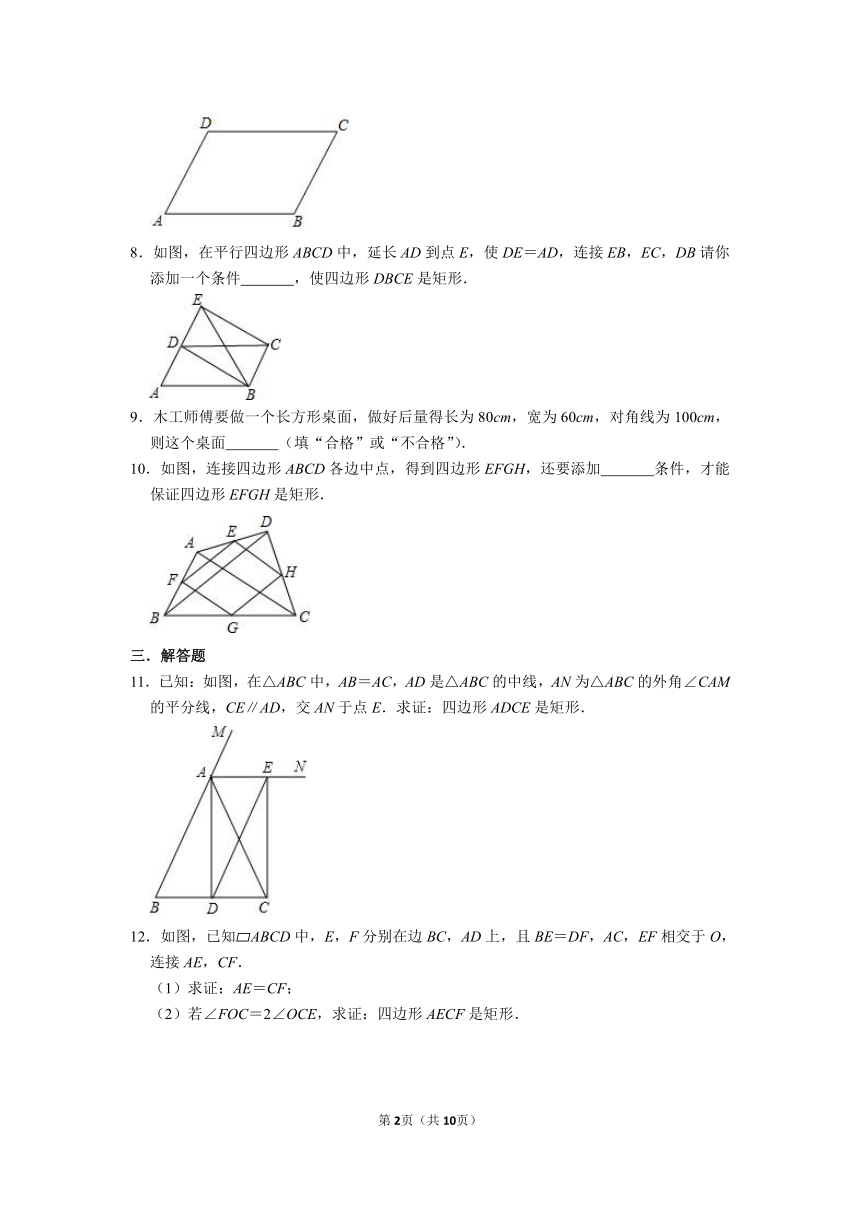

文档简介
6.2矩形的性质和判定
第2课时矩形的判定基础练
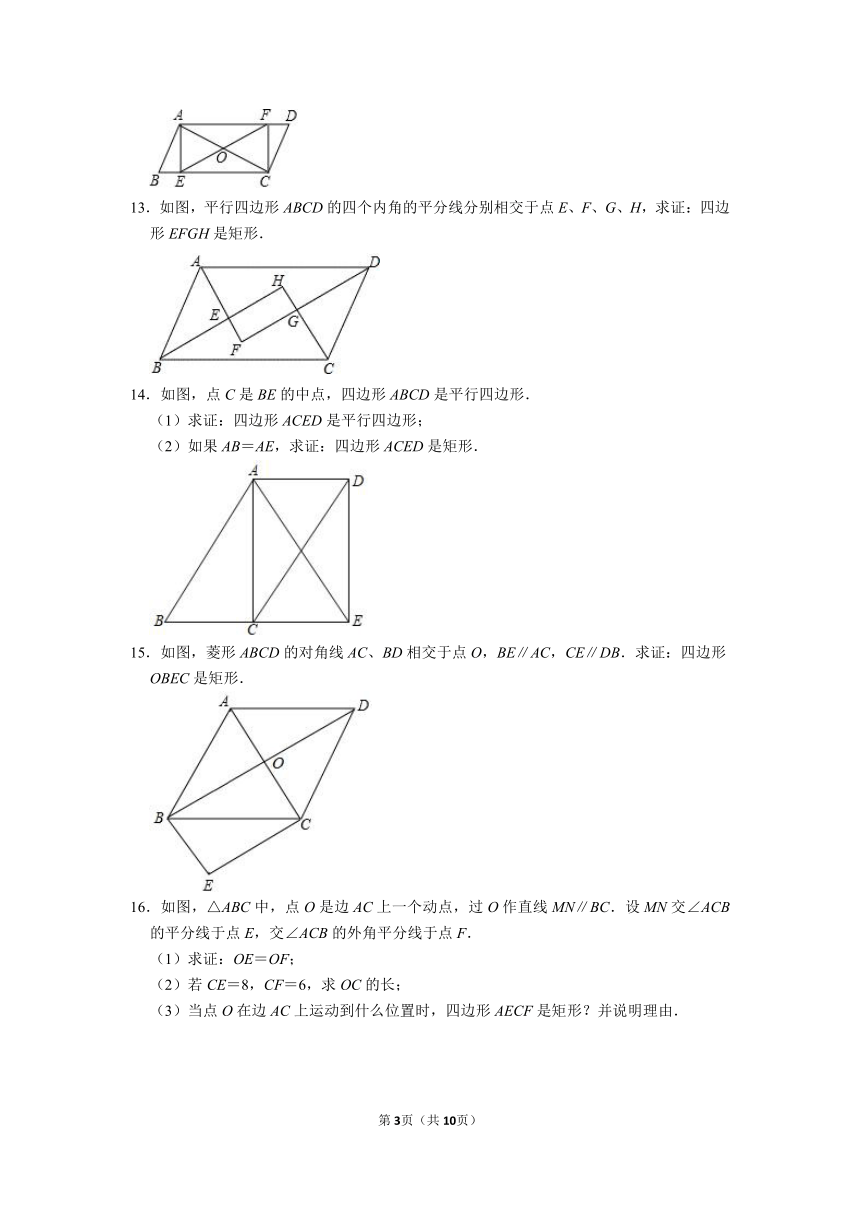
一.选择题
1.下列说法不正确的是( )
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.一个角是直角的四边形是矩形
2.在数学活动课上,老师要求同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量四边形其中的三个角是否都为直角
3.已知平行四边形ABCD中,下列条件:①AB=BC;②AC=BD;③AC⊥BD;④AC平分∠BAD,其中能说明平行四边形ABCD是矩形的是( )
A.① B.② C.③ D.④
4.能判定一个平行四边形是矩形的条件是( )
A.两条对角线互相平分 B.一组邻边相等
C.两条对角线相等 D.两条对角线互相垂直
5.如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等
B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形
D.若∠A=90°,则四边形AEDF是矩形
6. ABCD中,添加一个条件就成为矩形,则添加的条件是( )
A.AB=CD B.∠B+∠D=180°
C.AC=AD D.对角线互相垂直
二.填空题
7.如图,在平行四边形ABCD中,在不添加任何辅助线的情况下,请添加一个条件 ,使平行四边形ABCD是矩形.
8.如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB请你添加一个条件 ,使四边形DBCE是矩形.
9.木工师傅要做一个长方形桌面,做好后量得长为80cm,宽为60cm,对角线为100cm,则这个桌面 (填“合格”或“不合格”).
10.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加 条件,才能保证四边形EFGH是矩形.
三.解答题
11.已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
12.如图,已知 ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.
(1)求证:AE=CF;
(2)若∠FOC=2∠OCE,求证:四边形AECF是矩形.
13.如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.
14.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
15.如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.
16.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
17.如图,在 ABCD中,BE平分∠ABC,且与AD边交于点E,∠AEB=45°,证明:四边形ABCD是矩形.
18.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA相邻的外角平分线CF于点F,点O运动到何处时,四边形AECF是矩形?
参考答案
1.D.
2. D.
3. B.
4. C.
5.C.
【解析】A.连接EF,
∵D、E、F分别是△ABC各边中点,
∴EF∥BC,BD=CD,
设EF和BC间的距离为h,
∴S△BDEBD h,S△DCFCD h,
∴S△BDE=S△DCF,
故本选项不符合题意;
B.∵D、E、F分别是△ABC各边中点,
∴DE∥AC,DF∥AB,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形,
故本选项不符合题意;
C.∵D、E、F分别是△ABC各边中点,
∴EFBC,DFAB,
若AB=BC,则FE=DF,
∴四边形AEDF不一定是菱形,
故本选项符合题意;
D.∵四边形AEDF是平行四边形,
∴若∠A=90°,则四边形AEDF是矩形,
故本选项不符合题意;
故选:C.
6.B.
【解析】A、当AB=CD,不能判定 ABCD为矩形,故该选项不符合题意;
B、∵ ABCD中∠B=∠D,∠B+∠D=180°,
∴∠B=∠D=90°,
∴ ABCD是矩形;故该选项正确,符合题意;
C、∵AC=AD,不能得出 ABCD是矩形,故该选项不符合题意;
D、对角线互相垂直的平行四边形是菱形,故该选项不符合题意.
故选:B.
7.∠ABC=90°或AD⊥AB(答案不唯一).
【解析】理由:∵四边形ABCD是平行四边形,∠ABC=90°,
∴平行四边形ABCD是矩形(矩形的定义).
8.EB=DC.
【解析】添加EB=DC.理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴DE∥BC,
又∵DE=AD,
∴DE=BC,
∴四边形DBCE为平行四边形.
又∵EB=DC,
∴四边形DBCE是矩形.
9.合格.
10.AC⊥BD
【解析】∵G、H、E分别是BC、CD、AD的中点,
∴HG∥BD,EH∥AC,
∴∠EHG=∠1,∠1=∠2,
∴∠2=∠EHG,
∵四边形EFGH是矩形,
∴∠EHG=90°,
∴∠2=90°,
∴AC⊥BD.
故还要添加AC⊥BD,才能保证四边形EFGH是矩形.
11.证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE∥AD,
∴∠AEC=90°,
∴四边形ADCE为矩形.
12.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵BE=DF,
∴AF=CE,AF∥EC,
∴四边形AECF是平行四边形,
∴AE=CF.
(2)∵∠FOC=∠OEC+∠OCE=2∠OCE,
∴∠OEC=∠OCE,
∴OE=OC,
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∴AC=EF,
∴四边形AECF是矩形.
13.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC∠ABC,∠HCB∠BCD,
∴∠HBC+∠HCB(∠ABC+∠BCD)180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.
14.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵点C是BE的中点,
∴BC=CE,
∴AD=CE,
∵AD∥CE,
∴四边形ACED是平行四边形;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=DC,
∵AB=AE,
∴DC=AE,
∵四边形ACED是平行四边形,
∴四边形ACED是矩形.
15.证明:∵BE∥AC,CE∥DB,
∴四边形OBEC是平行四边形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOB=90°,
∴平行四边形OBEC是矩形.
16.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF10,
∴OCEF=5;
(3)答:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
17.证明:∵四边形ABCD为平行四边形
∴AD∥BC
∴∠AEB=∠EBC
∵BE平分∠ABC,∠AEB=45°
∴∠ABE=∠EBC=45°
∴∠ABC=90°
∴四边形ABCD是矩形
18.证明:∵CE平分∠ACB,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO.
当点O运动到AC的中点时,四边形AECF是“平行四边形”,当∠ECF=90度时,平行四边形AECF是矩形,
∵EO=FO,点O是AC的中点.
∴四边形AECF是平行四边形,
∵CF平分∠BCA的外角,
∴∠4=∠5,
又∵∠1=∠2,
∴∠2+∠4180°=90°.
即∠ECF=90度,
∴平行四边形AECF是矩形.
第4页(共9页)
第2课时矩形的判定基础练
一.选择题
1.下列说法不正确的是( )
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.一个角是直角的四边形是矩形
2.在数学活动课上,老师要求同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量四边形其中的三个角是否都为直角
3.已知平行四边形ABCD中,下列条件:①AB=BC;②AC=BD;③AC⊥BD;④AC平分∠BAD,其中能说明平行四边形ABCD是矩形的是( )
A.① B.② C.③ D.④
4.能判定一个平行四边形是矩形的条件是( )
A.两条对角线互相平分 B.一组邻边相等
C.两条对角线相等 D.两条对角线互相垂直
5.如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等
B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形
D.若∠A=90°,则四边形AEDF是矩形
6. ABCD中,添加一个条件就成为矩形,则添加的条件是( )
A.AB=CD B.∠B+∠D=180°
C.AC=AD D.对角线互相垂直
二.填空题
7.如图,在平行四边形ABCD中,在不添加任何辅助线的情况下,请添加一个条件 ,使平行四边形ABCD是矩形.
8.如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB请你添加一个条件 ,使四边形DBCE是矩形.
9.木工师傅要做一个长方形桌面,做好后量得长为80cm,宽为60cm,对角线为100cm,则这个桌面 (填“合格”或“不合格”).
10.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加 条件,才能保证四边形EFGH是矩形.
三.解答题
11.已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
12.如图,已知 ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.
(1)求证:AE=CF;
(2)若∠FOC=2∠OCE,求证:四边形AECF是矩形.
13.如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.
14.如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
15.如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.
16.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
17.如图,在 ABCD中,BE平分∠ABC,且与AD边交于点E,∠AEB=45°,证明:四边形ABCD是矩形.
18.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA相邻的外角平分线CF于点F,点O运动到何处时,四边形AECF是矩形?
参考答案
1.D.
2. D.
3. B.
4. C.
5.C.
【解析】A.连接EF,
∵D、E、F分别是△ABC各边中点,
∴EF∥BC,BD=CD,
设EF和BC间的距离为h,
∴S△BDEBD h,S△DCFCD h,
∴S△BDE=S△DCF,
故本选项不符合题意;
B.∵D、E、F分别是△ABC各边中点,
∴DE∥AC,DF∥AB,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形,
故本选项不符合题意;
C.∵D、E、F分别是△ABC各边中点,
∴EFBC,DFAB,
若AB=BC,则FE=DF,
∴四边形AEDF不一定是菱形,
故本选项符合题意;
D.∵四边形AEDF是平行四边形,
∴若∠A=90°,则四边形AEDF是矩形,
故本选项不符合题意;
故选:C.
6.B.
【解析】A、当AB=CD,不能判定 ABCD为矩形,故该选项不符合题意;
B、∵ ABCD中∠B=∠D,∠B+∠D=180°,
∴∠B=∠D=90°,
∴ ABCD是矩形;故该选项正确,符合题意;
C、∵AC=AD,不能得出 ABCD是矩形,故该选项不符合题意;
D、对角线互相垂直的平行四边形是菱形,故该选项不符合题意.
故选:B.
7.∠ABC=90°或AD⊥AB(答案不唯一).
【解析】理由:∵四边形ABCD是平行四边形,∠ABC=90°,
∴平行四边形ABCD是矩形(矩形的定义).
8.EB=DC.
【解析】添加EB=DC.理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴DE∥BC,
又∵DE=AD,
∴DE=BC,
∴四边形DBCE为平行四边形.
又∵EB=DC,
∴四边形DBCE是矩形.
9.合格.
10.AC⊥BD
【解析】∵G、H、E分别是BC、CD、AD的中点,
∴HG∥BD,EH∥AC,
∴∠EHG=∠1,∠1=∠2,
∴∠2=∠EHG,
∵四边形EFGH是矩形,
∴∠EHG=90°,
∴∠2=90°,
∴AC⊥BD.
故还要添加AC⊥BD,才能保证四边形EFGH是矩形.
11.证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE∥AD,
∴∠AEC=90°,
∴四边形ADCE为矩形.
12.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵BE=DF,
∴AF=CE,AF∥EC,
∴四边形AECF是平行四边形,
∴AE=CF.
(2)∵∠FOC=∠OEC+∠OCE=2∠OCE,
∴∠OEC=∠OCE,
∴OE=OC,
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∴AC=EF,
∴四边形AECF是矩形.
13.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC∠ABC,∠HCB∠BCD,
∴∠HBC+∠HCB(∠ABC+∠BCD)180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.
14.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵点C是BE的中点,
∴BC=CE,
∴AD=CE,
∵AD∥CE,
∴四边形ACED是平行四边形;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=DC,
∵AB=AE,
∴DC=AE,
∵四边形ACED是平行四边形,
∴四边形ACED是矩形.
15.证明:∵BE∥AC,CE∥DB,
∴四边形OBEC是平行四边形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOB=90°,
∴平行四边形OBEC是矩形.
16.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF10,
∴OCEF=5;
(3)答:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
17.证明:∵四边形ABCD为平行四边形
∴AD∥BC
∴∠AEB=∠EBC
∵BE平分∠ABC,∠AEB=45°
∴∠ABE=∠EBC=45°
∴∠ABC=90°
∴四边形ABCD是矩形
18.证明:∵CE平分∠ACB,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO.
当点O运动到AC的中点时,四边形AECF是“平行四边形”,当∠ECF=90度时,平行四边形AECF是矩形,
∵EO=FO,点O是AC的中点.
∴四边形AECF是平行四边形,
∵CF平分∠BCA的外角,
∴∠4=∠5,
又∵∠1=∠2,
∴∠2+∠4180°=90°.
即∠ECF=90度,
∴平行四边形AECF是矩形.
第4页(共9页)
