2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质和判定第3课时矩形性质与判定提升练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质和判定第3课时矩形性质与判定提升练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 169.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 22:48:39 | ||
图片预览



文档简介
6.2矩形的性质和判定
第3课时矩形性质与判定提升练
一.选择题
1.下列四个命题中,正确的是( )
A.对角线相等的四边形是矩形
B.有一个角是直角的四边形是矩形
C.两组对边分别相等的四边形是矩形
D.四个角都相等的四边形是矩形
2.如图,四边形ABCD的对角线相交于点O,且互相平分.若添加下列条件,不能判定四边形ABCD为矩形的是( )
A.AC=BD B.∠DAB=90°
C.AB=AD D.∠ADC+∠ABC=180°
3.如图,矩形ABCD中,DE⊥AC于E,若∠ADE=2∠EDC,则∠BDE的度数为( )
A.36° B.30° C.27° D.18°
4.如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
①DC=3OG;②OGBC;③△OGE是等边三角形;④S△AOES矩形ABCD.
A.1个 B.2个 C.3个 D.4个
5.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.1.2 B.1.3 C.1.4 D.2.4
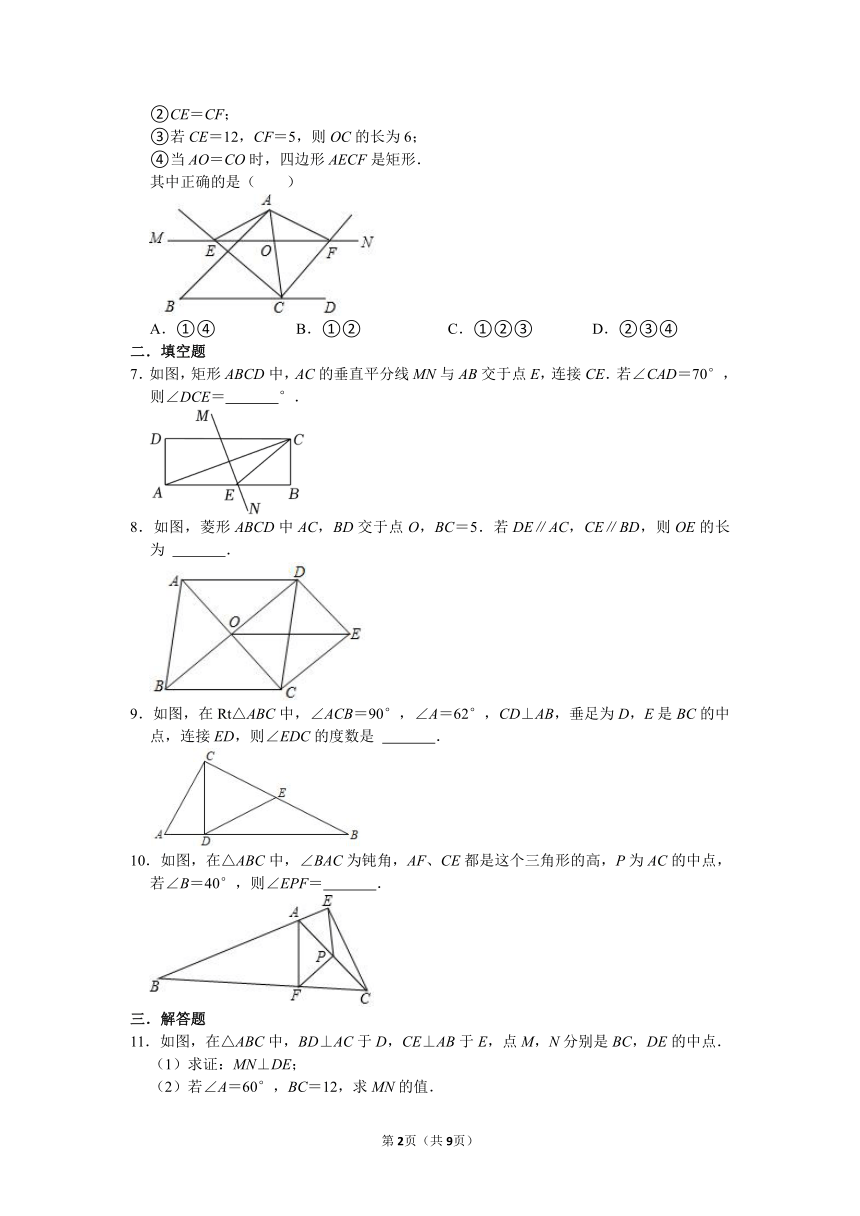
6.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:
①OE=OF;
②CE=CF;
③若CE=12,CF=5,则OC的长为6;
④当AO=CO时,四边形AECF是矩形.
其中正确的是( )
A.①④ B.①② C.①②③ D.②③④
二.填空题
7.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE= °.
8.如图,菱形ABCD中AC,BD交于点O,BC=5.若DE∥AC,CE∥BD,则OE的长为 .
9.如图,在Rt△ABC中,∠ACB=90°,∠A=62°,CD⊥AB,垂足为D,E是BC的中点,连接ED,则∠EDC的度数是 .
10.如图,在△ABC中,∠BAC为钝角,AF、CE都是这个三角形的高,P为AC的中点,若∠B=40°,则∠EPF= .
三.解答题
11.如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,点M,N分别是BC,DE的中点.
(1)求证:MN⊥DE;
(2)若∠A=60°,BC=12,求MN的值.
12.如图,菱形ABCD的对角线AC与BD交于点O,分别过点C、点D作BD、AC的平行线交于点E,连接EO交CD于点F.
(1)求证:四边形DECO是矩形;
(2)若AD=3,求OE的长.
13.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=13,EF=5,求OE和BG的长.
14.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠ABC=60°,求四边形AODE的面积.
15.如图,菱形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,且BEAC,连接EC.
(1)求证:四边形BECO是矩形;
(2)连接ED交AC于点F,连接BF,若AC=12,AB=10,BF= .
16.如图.平行四边形ABCD中,AD=2AB,M、N分别为AD、BC的中点,AN、BM交于点P,CM、DN交于点Q.求证:
(1)四边形ABNM为菱形;
(2)四边形PNQM为矩形.
参考答案
1. D.
2. C.
3. B.
【解析】在矩形ABCD中,∠ADC=90°.
∵∠ADE=2∠EDC,
∴∠ADE=60°,∠EDC=30°,
∵DE⊥AC,
∴∠DCE=90°﹣30°=60°,
∵OD=OC,
∴∠ODC=∠OCD=60°,
∴∠DOC=180°﹣2×60°=60°
∴∠BDE=90°﹣∠DOC=30°.
4.C
【解析】∵EF⊥AC,点G是AE中点,
∴OG=AG=GEAE,
∵∠AOG=30°,
∴∠OAG=∠AOG=30°,∠GOE=90°﹣∠AOG=90°﹣30°=60°,
∴△OGE是等边三角形,故③正确;
设AE=2a,则OE=OG=a,
由勾股定理得,AOa,
∵O为AC中点,
∴AC=2AO=2a,
∴BCAC2aa,
在Rt△ABC中,由勾股定理得,AB3a,
∵四边形ABCD是矩形,
∴CD=AB=3a,
∴DC=3OG,故①正确;
∵OG=a,BCa,
∴OGBC,故②错误;
∵S△AOEa aa2,S矩形ABCD=3a a=3a2,
∴S△AOES矩形ABCD,故④正确;
综上所述,结论正确的是①③④,
故选:C.
5.A【解析】连接AP,如图所示:
∵∠BAC=90°,AB=3,AC=4,
∴BC5,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴PMAP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样PM也最短,
∴当AP⊥BC时,AP2.4,
∴AP最短时,AP=2.4,
∴当PM最短时,PMAP=1.2.
故选:A.
6.A
【解析】∵MN∥CB,
∴∠OEC=∠BCE,∠OFC=∠ACF
∵∠ACE=∠BCE,∠ACF=∠DCF,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴OC=OE=OF,故①正确,
∵∠BCD=180°,
∴∠ECF=90°,
若EC=CF,则∠OFC=45°,显然不可能,故②错误,
∵∠ECF=90°,EC=12,CF=5,
∴EF13,
∴OCEF=6.5,故③错误,
∴OE=OF,OA=OC,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴四边形AECF是矩形.
故选:A.
7.40.
【解析】∵MN是AC的垂直平分线,
∴EC=EA,
∴∠ECA=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,∠D=90°,
∴∠DCA=∠EAC=90°﹣70°=20°,
∴∠DCE=∠DCA+∠ECA=20°+20°=40°,
8.5
【解析】∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,
∵四边形ABCD是菱形,
∴BC=CD=5,AC⊥BD,
∴∠COD=90°,
∴平行四边形ODEC是矩形,
∴OE=CD=5,
9. 62°
【解析】∵∠ACB=90°,∠A=62°,
∴∠B=90°﹣∠A=90°﹣62°=28°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠DCE=90°﹣∠B=90°﹣28°=62°,
∵E是BC的中点,
∴DE,CEBC,
∴DE=CE,
∴∠EDC=∠DCE=62°,
10. 100°.
【解析】∵CE⊥BA,∠B=40°,
∴∠BCE=50°,
∵AF⊥BC,CE⊥BA,P为AC的中点,
∴PFAC=PC,PEAC=PC,
∴∠PFC=∠PCF,∠PEC=∠PCE,
∴∠EPF=2∠PCF+2∠PCE=2∠BCE=100°,
11.(1)证明:∵BD⊥AC于D,CE⊥AB于E,点M是BC的中点,
∴MD=MEBC,
∴点N是DE的中点,
∴MN⊥DE;
(2)解:∵MD=ME=BM=CM,
∴∠BME+∠CMD=180°﹣2∠ABC+180°﹣2∠ACB=360°﹣2(∠ABC+∠ACB),
∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∴∠BME+∠CMD=360°﹣2×120°=120°,
∴∠DME=60°,
∴△MED是等边三角形,
∴DE=DM,
有(1)知DMBC=6,
∴DE=6,
∵N是DE的中点,
∴DNDE=3,
∴MN3.
12.(1)证明:∵CE∥BD,DE∥AC,
∴四边形DECO是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形DECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴CD=AD=3,
由(1)得:四边形DECO是矩形,
∴OE=CD=3.
13.(1)证明:∵四边形ABCD为菱形,
∴点O为BD的中点,
∵点E为AD中点,
∴OE为△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG为平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG为矩形.
(2)解:∵点E为AD的中点,AD=13,
∴AE=6.5,
∵EF⊥AB,
∴∠EFA=90°,EF=5,
∴,
∵四边形ABCD为菱形,
∴AB=AD=13,AC⊥BD,
∴OEAD=6.5,
∵四边形OEFG为矩形,
∴FG=OE=6.5,
∴BG=AB﹣AF﹣FG.
14.(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∴平行四边形AODE是矩形;
(2)解:∵四边形ABCD是菱形,
∴AD=AB=BC=6,OA=OC,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=6,
∴OAAC=3,
在Rt△AOD中,由勾股定理得:OD3,
由(1)得:四边形AODE是矩形,
∴四边形AODE的面积=OA OD=3×39.
15.(1)证明:∵四边形ABCD是菱形,
∴∠BOC=90°,OC=OAAC,
∵BEAC,
∴BE=OC,
∵BE∥AC,
∴四边形BECO是平行四边形,
∵∠BOC=90°,
∴平行四边形BECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴BC=AB=10,OCAC=6,OB=OD,AC⊥BD,
在Rt△OBC中,由勾股定理得:OB8,
∴BD=2OB=16,
由(1)得:四边形BECO是矩形,
∴BE=OC=6,∠OBE=∠ECO=90°,OB=CE,OB∥CE,
∴DE2,∠ODF=∠CEF,OD=CE,
在△ODF和△CEF中,
,
∴△ODF≌△CEF(ASA),
∴DF=EF,
∵∠DBE=90°,
∴BFDE,
故答案为:.
16.证明:(1)∵四边形ABCD是平行四边形,点M、N分别为AD、BC中点,
∴AM∥BN.AMAD,BNCD,AD=BC.(2分)
∴AM=BN,∴ABNM是平行四边形.(1分)
∵AD=2AB,∴ABAD,∴AB=AM.(1分)
∴四边形ABNM是菱形.(1分)
(2)∵四边形ABNM是菱形,
∴∠MPN=90°,∠BNA=∠MNA.(2分)
同理可得:四边形MNCD是菱形.
∠MQN=90°,∠MND=∠CND.(1分)
∴∠MNA+∠MND=90°.(1分)
∴四边形PNQM为矩形.(1分)第1页(共10页)
第3课时矩形性质与判定提升练
一.选择题
1.下列四个命题中,正确的是( )
A.对角线相等的四边形是矩形
B.有一个角是直角的四边形是矩形
C.两组对边分别相等的四边形是矩形
D.四个角都相等的四边形是矩形
2.如图,四边形ABCD的对角线相交于点O,且互相平分.若添加下列条件,不能判定四边形ABCD为矩形的是( )
A.AC=BD B.∠DAB=90°
C.AB=AD D.∠ADC+∠ABC=180°
3.如图,矩形ABCD中,DE⊥AC于E,若∠ADE=2∠EDC,则∠BDE的度数为( )
A.36° B.30° C.27° D.18°
4.如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
①DC=3OG;②OGBC;③△OGE是等边三角形;④S△AOES矩形ABCD.
A.1个 B.2个 C.3个 D.4个
5.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.1.2 B.1.3 C.1.4 D.2.4
6.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:
①OE=OF;
②CE=CF;
③若CE=12,CF=5,则OC的长为6;
④当AO=CO时,四边形AECF是矩形.
其中正确的是( )
A.①④ B.①② C.①②③ D.②③④
二.填空题
7.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE= °.
8.如图,菱形ABCD中AC,BD交于点O,BC=5.若DE∥AC,CE∥BD,则OE的长为 .
9.如图,在Rt△ABC中,∠ACB=90°,∠A=62°,CD⊥AB,垂足为D,E是BC的中点,连接ED,则∠EDC的度数是 .
10.如图,在△ABC中,∠BAC为钝角,AF、CE都是这个三角形的高,P为AC的中点,若∠B=40°,则∠EPF= .
三.解答题
11.如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,点M,N分别是BC,DE的中点.
(1)求证:MN⊥DE;
(2)若∠A=60°,BC=12,求MN的值.
12.如图,菱形ABCD的对角线AC与BD交于点O,分别过点C、点D作BD、AC的平行线交于点E,连接EO交CD于点F.
(1)求证:四边形DECO是矩形;
(2)若AD=3,求OE的长.
13.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=13,EF=5,求OE和BG的长.
14.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠ABC=60°,求四边形AODE的面积.
15.如图,菱形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,且BEAC,连接EC.
(1)求证:四边形BECO是矩形;
(2)连接ED交AC于点F,连接BF,若AC=12,AB=10,BF= .
16.如图.平行四边形ABCD中,AD=2AB,M、N分别为AD、BC的中点,AN、BM交于点P,CM、DN交于点Q.求证:
(1)四边形ABNM为菱形;
(2)四边形PNQM为矩形.
参考答案
1. D.
2. C.
3. B.
【解析】在矩形ABCD中,∠ADC=90°.
∵∠ADE=2∠EDC,
∴∠ADE=60°,∠EDC=30°,
∵DE⊥AC,
∴∠DCE=90°﹣30°=60°,
∵OD=OC,
∴∠ODC=∠OCD=60°,
∴∠DOC=180°﹣2×60°=60°
∴∠BDE=90°﹣∠DOC=30°.
4.C
【解析】∵EF⊥AC,点G是AE中点,
∴OG=AG=GEAE,
∵∠AOG=30°,
∴∠OAG=∠AOG=30°,∠GOE=90°﹣∠AOG=90°﹣30°=60°,
∴△OGE是等边三角形,故③正确;
设AE=2a,则OE=OG=a,
由勾股定理得,AOa,
∵O为AC中点,
∴AC=2AO=2a,
∴BCAC2aa,
在Rt△ABC中,由勾股定理得,AB3a,
∵四边形ABCD是矩形,
∴CD=AB=3a,
∴DC=3OG,故①正确;
∵OG=a,BCa,
∴OGBC,故②错误;
∵S△AOEa aa2,S矩形ABCD=3a a=3a2,
∴S△AOES矩形ABCD,故④正确;
综上所述,结论正确的是①③④,
故选:C.
5.A【解析】连接AP,如图所示:
∵∠BAC=90°,AB=3,AC=4,
∴BC5,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴PMAP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样PM也最短,
∴当AP⊥BC时,AP2.4,
∴AP最短时,AP=2.4,
∴当PM最短时,PMAP=1.2.
故选:A.
6.A
【解析】∵MN∥CB,
∴∠OEC=∠BCE,∠OFC=∠ACF
∵∠ACE=∠BCE,∠ACF=∠DCF,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴OC=OE=OF,故①正确,
∵∠BCD=180°,
∴∠ECF=90°,
若EC=CF,则∠OFC=45°,显然不可能,故②错误,
∵∠ECF=90°,EC=12,CF=5,
∴EF13,
∴OCEF=6.5,故③错误,
∴OE=OF,OA=OC,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴四边形AECF是矩形.
故选:A.
7.40.
【解析】∵MN是AC的垂直平分线,
∴EC=EA,
∴∠ECA=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,∠D=90°,
∴∠DCA=∠EAC=90°﹣70°=20°,
∴∠DCE=∠DCA+∠ECA=20°+20°=40°,
8.5
【解析】∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,
∵四边形ABCD是菱形,
∴BC=CD=5,AC⊥BD,
∴∠COD=90°,
∴平行四边形ODEC是矩形,
∴OE=CD=5,
9. 62°
【解析】∵∠ACB=90°,∠A=62°,
∴∠B=90°﹣∠A=90°﹣62°=28°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠DCE=90°﹣∠B=90°﹣28°=62°,
∵E是BC的中点,
∴DE,CEBC,
∴DE=CE,
∴∠EDC=∠DCE=62°,
10. 100°.
【解析】∵CE⊥BA,∠B=40°,
∴∠BCE=50°,
∵AF⊥BC,CE⊥BA,P为AC的中点,
∴PFAC=PC,PEAC=PC,
∴∠PFC=∠PCF,∠PEC=∠PCE,
∴∠EPF=2∠PCF+2∠PCE=2∠BCE=100°,
11.(1)证明:∵BD⊥AC于D,CE⊥AB于E,点M是BC的中点,
∴MD=MEBC,
∴点N是DE的中点,
∴MN⊥DE;
(2)解:∵MD=ME=BM=CM,
∴∠BME+∠CMD=180°﹣2∠ABC+180°﹣2∠ACB=360°﹣2(∠ABC+∠ACB),
∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∴∠BME+∠CMD=360°﹣2×120°=120°,
∴∠DME=60°,
∴△MED是等边三角形,
∴DE=DM,
有(1)知DMBC=6,
∴DE=6,
∵N是DE的中点,
∴DNDE=3,
∴MN3.
12.(1)证明:∵CE∥BD,DE∥AC,
∴四边形DECO是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形DECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴CD=AD=3,
由(1)得:四边形DECO是矩形,
∴OE=CD=3.
13.(1)证明:∵四边形ABCD为菱形,
∴点O为BD的中点,
∵点E为AD中点,
∴OE为△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG为平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG为矩形.
(2)解:∵点E为AD的中点,AD=13,
∴AE=6.5,
∵EF⊥AB,
∴∠EFA=90°,EF=5,
∴,
∵四边形ABCD为菱形,
∴AB=AD=13,AC⊥BD,
∴OEAD=6.5,
∵四边形OEFG为矩形,
∴FG=OE=6.5,
∴BG=AB﹣AF﹣FG.
14.(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∴平行四边形AODE是矩形;
(2)解:∵四边形ABCD是菱形,
∴AD=AB=BC=6,OA=OC,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=6,
∴OAAC=3,
在Rt△AOD中,由勾股定理得:OD3,
由(1)得:四边形AODE是矩形,
∴四边形AODE的面积=OA OD=3×39.
15.(1)证明:∵四边形ABCD是菱形,
∴∠BOC=90°,OC=OAAC,
∵BEAC,
∴BE=OC,
∵BE∥AC,
∴四边形BECO是平行四边形,
∵∠BOC=90°,
∴平行四边形BECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴BC=AB=10,OCAC=6,OB=OD,AC⊥BD,
在Rt△OBC中,由勾股定理得:OB8,
∴BD=2OB=16,
由(1)得:四边形BECO是矩形,
∴BE=OC=6,∠OBE=∠ECO=90°,OB=CE,OB∥CE,
∴DE2,∠ODF=∠CEF,OD=CE,
在△ODF和△CEF中,
,
∴△ODF≌△CEF(ASA),
∴DF=EF,
∵∠DBE=90°,
∴BFDE,
故答案为:.
16.证明:(1)∵四边形ABCD是平行四边形,点M、N分别为AD、BC中点,
∴AM∥BN.AMAD,BNCD,AD=BC.(2分)
∴AM=BN,∴ABNM是平行四边形.(1分)
∵AD=2AB,∴ABAD,∴AB=AM.(1分)
∴四边形ABNM是菱形.(1分)
(2)∵四边形ABNM是菱形,
∴∠MPN=90°,∠BNA=∠MNA.(2分)
同理可得:四边形MNCD是菱形.
∠MQN=90°,∠MND=∠CND.(1分)
∴∠MNA+∠MND=90°.(1分)
∴四边形PNQM为矩形.(1分)第1页(共10页)
