华东师大版八年级下册数学 19.2.1 课件(共17张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.2.1 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 963.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 15:27:26 | ||
图片预览




文档简介
(共17张PPT)
华师版数学八年级下
数
求ax+b=0(a≠0)的解
y=ax+b 当y=0时x的取值
形
求ax+b>0(a≠0)的解
y=ax+b 当y>0时x的取值范围
求ax+b<0(a≠0)的解
y=ax+b 当y<0时x的取值范围
y=ax+b的图像与x轴交点的横坐标
y=ax+b在x轴上方的图像对应的x值
y=ax+b在x轴下方的图像对应的x值
数
形
数
形
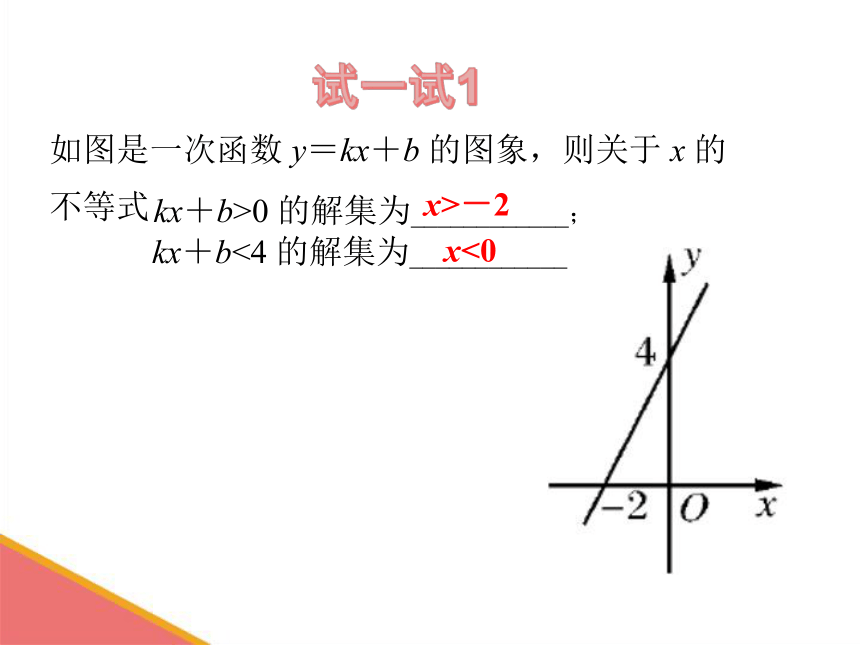
如图是一次函数 y=kx+b 的图象,则关于 x 的
不等式
x>-2
kx+b>0 的解集为____________;
kx+b<4 的解集为____________
x<0
问题情境
你会解下面方程组和不等式吗?
(1)
(2) 2x+1>-x+4;
(3) .
y=10X
y=40x-120;
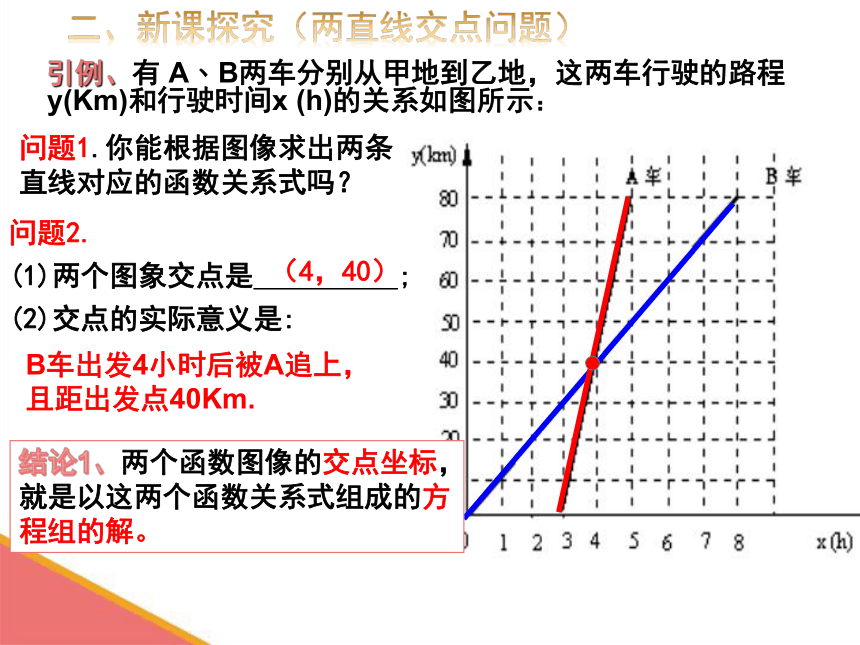
问题1.你能根据图像求出两条直线对应的函数关系式吗?
问题2.
(1)两个图象交点是 ;
(2)交点的实际意义是:
B车出发4小时后被A追上,且距出发点40Km.
(4,40)
引例、有 A﹑B两车分别从甲地到乙地,这两车行驶的路程y(Km)和行驶时间x (h)的关系如图所示:
方程组
1
2
3
4
2
3
4
1
-1
0
-1
l1
l2
y
x
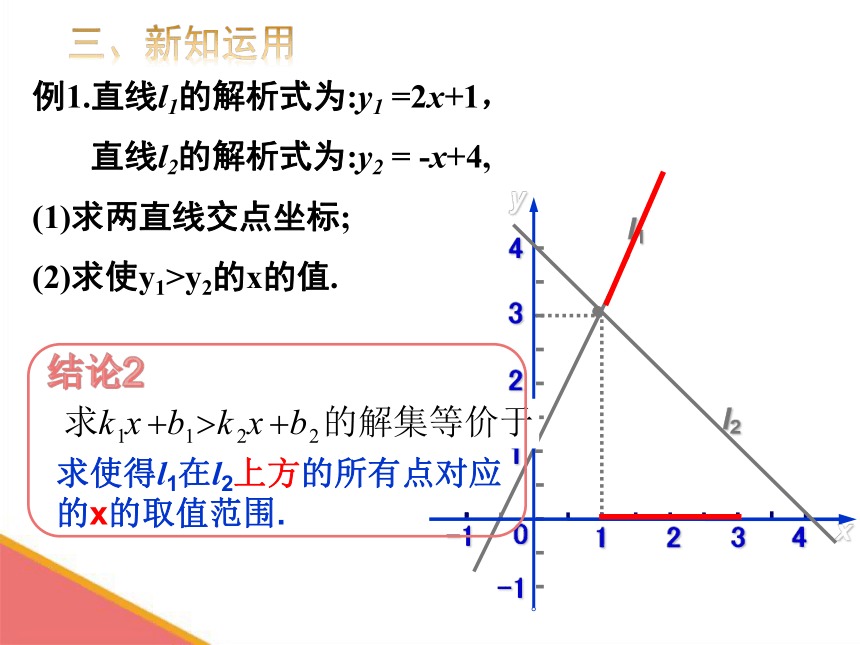
例1.直线l1的解析式为:y1 =2x+1,
直线l2的解析式为:y2 = -x+4,
(1)求两直线交点坐标;
(2)求使y1>y2的x的值.
求使得l1在l2上方的所有点对应
的x的取值范围.
例2.如图,直线l1:y1 =x+1与直线l2:y2 = mx+3
相交于点P(1,b).
(1)求b的值;
y=x+1
(2)求方程组 的解.
y=mx+3
(3)求使y1求使得l1在l2 下方的所有点对应
的x的取值范围.
议一议:
解二元一次方程组和不等式都可直接利用消元法求得,为何要学习利用图像解呢
例2摇身一变:
如图,直线l1:y1=x+1与直线l2:y2= mx+n
相交于点P(1,b).
(1)求b的值;
y=x+1
(2)求方程组 的解.
y=mx+n
(3)求使y1求使得l1在l2上方的所有点对应
的x的取值范围.
求使得l1在l2 下方的所有点对应
的x的取值范围.
x=-1
y=1.5
x=-1
x>-1
x<-1
例3 利用图象解不等式:
x≤-2
-2(1,-2)
(-2,1)
(-2,1)
(-1,2)
求使得l1在l2上方的所有点对应
的x的取值范围.
求使得l1在l2 下方的所有点对应
的x的取值范围.
华师版数学八年级下
数
求ax+b=0(a≠0)的解
y=ax+b 当y=0时x的取值
形
求ax+b>0(a≠0)的解
y=ax+b 当y>0时x的取值范围
求ax+b<0(a≠0)的解
y=ax+b 当y<0时x的取值范围
y=ax+b的图像与x轴交点的横坐标
y=ax+b在x轴上方的图像对应的x值
y=ax+b在x轴下方的图像对应的x值
数
形
数
形
如图是一次函数 y=kx+b 的图象,则关于 x 的
不等式
x>-2
kx+b>0 的解集为____________;
kx+b<4 的解集为____________
x<0
问题情境
你会解下面方程组和不等式吗?
(1)
(2) 2x+1>-x+4;
(3) .
y=10X
y=40x-120;
问题1.你能根据图像求出两条直线对应的函数关系式吗?
问题2.
(1)两个图象交点是 ;
(2)交点的实际意义是:
B车出发4小时后被A追上,且距出发点40Km.
(4,40)
引例、有 A﹑B两车分别从甲地到乙地,这两车行驶的路程y(Km)和行驶时间x (h)的关系如图所示:
方程组
1
2
3
4
2
3
4
1
-1
0
-1
l1
l2
y
x
例1.直线l1的解析式为:y1 =2x+1,
直线l2的解析式为:y2 = -x+4,
(1)求两直线交点坐标;
(2)求使y1>y2的x的值.
求使得l1在l2上方的所有点对应
的x的取值范围.
例2.如图,直线l1:y1 =x+1与直线l2:y2 = mx+3
相交于点P(1,b).
(1)求b的值;
y=x+1
(2)求方程组 的解.
y=mx+3
(3)求使y1
的x的取值范围.
议一议:
解二元一次方程组和不等式都可直接利用消元法求得,为何要学习利用图像解呢
例2摇身一变:
如图,直线l1:y1=x+1与直线l2:y2= mx+n
相交于点P(1,b).
(1)求b的值;
y=x+1
(2)求方程组 的解.
y=mx+n
(3)求使y1
的x的取值范围.
求使得l1在l2 下方的所有点对应
的x的取值范围.
x=-1
y=1.5
x=-1
x>-1
x<-1
例3 利用图象解不等式:
x≤-2
-2
(-2,1)
(-2,1)
(-1,2)
求使得l1在l2上方的所有点对应
的x的取值范围.
求使得l1在l2 下方的所有点对应
的x的取值范围.
