华东师大版八年级下册数学 小结 课件(共23张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 小结 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 15:29:39 | ||
图片预览






文档简介
(共23张PPT)
小结
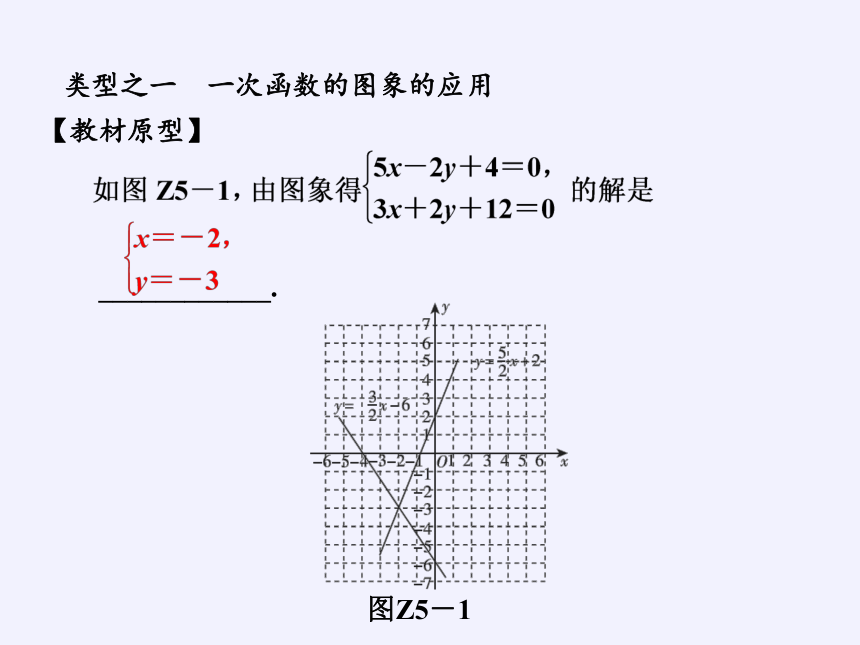
类型之一 一次函数的图象的应用
【教材原型】
____________.
图Z5-1
【思想方法】 (1)每个二元一次方程组都对应着两个一次函数,于是也对应着两条直线.从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线的交点坐标;
(2)一次函数、一元一次方程、一元一次不等式有着独立的概念,但在本质上,后者是前者的特殊情况,从而可以利用函数图象解决方程或方程组问题,体现数形结合思想.
【中考变形】
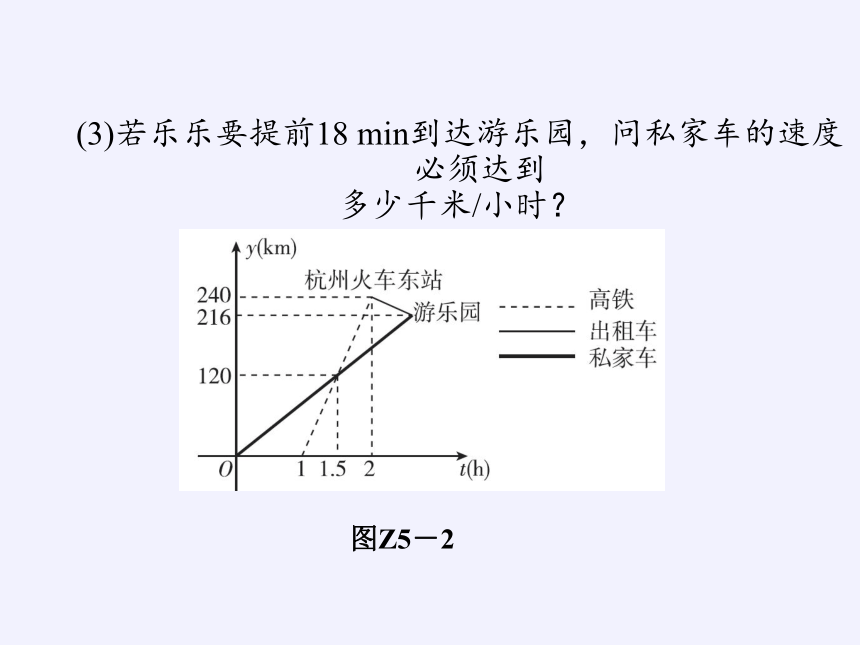
1.[2015·衢州改编]高铁的开通,给衢州市民出行带来了极大的方便.五一期间,乐乐和颖颖相约到杭州市某游乐园游玩,乐乐乘私家车从衢州出发1 h后,颖颖乘坐高铁从衢州出发,先到杭州火车东站,然后转乘出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(km)与乘车时间t(h)的关系如图Z5-2所示.请结合图象解决下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)当颖颖到达杭州火车东站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18 min到达游乐园,问私家车的速度必须达到
多少千米/小时?
图Z5-2
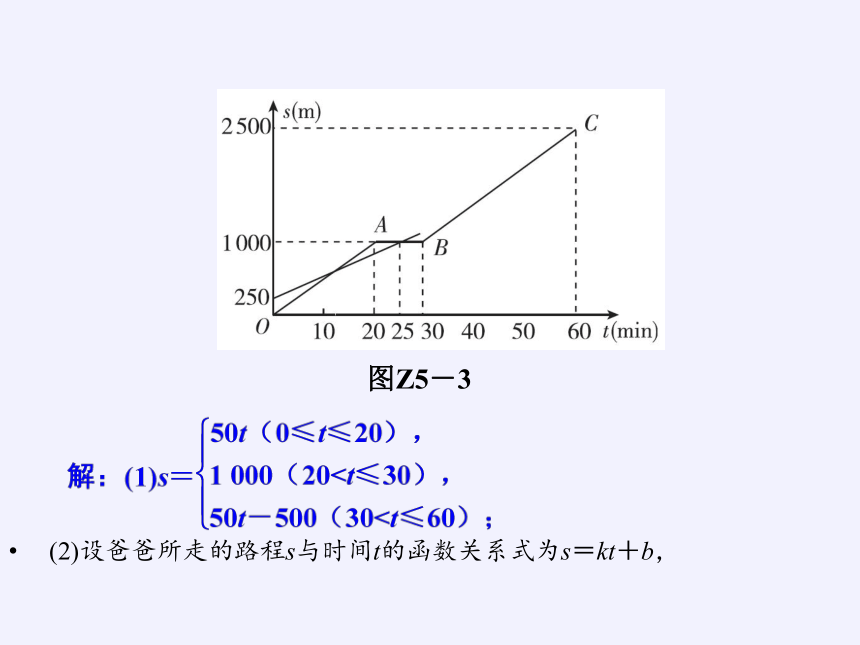
2.[2016·南充]小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2 500 m,如图Z5-3是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20 min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
(2)设爸爸所走的路程s与时间t的函数关系式为s=kt+b,
图Z5-3
则爸爸所走的路程与步行时间的关系式为s=30t+250,
小明与爸爸第三次相遇应该是t>30 min时,
当50t-500=30t+250,即t=37.5 min时,小明与爸爸第三次相遇;
(3)30t+250=2 500,解得t=75,
则爸爸到达公园需要75 min,
∵小明到达公园需要的时间是60 min,
如果小明希望比爸爸早20 min到达公园,则小明在步行过程中停留的时间需减少5 min.
【中考预测】
甲、乙两人同时从相距90 km的A地前往B
地,甲乘汽车,乙骑摩托车,甲到达B地
停留半个小时后返回A地,如图Z5-5是
他们离A地的距离y(km)与时间x(h)之间的
函数关系图象.
(1)求甲从B地返回A地的过程中,y与x之间
的函数关系式,并写出自变量的取值范围;
(2)若乙出发后2 h和甲相遇,求乙从A地到B地用了多长
时间?
图Z5-5
解:(1)设函数关系式为y=kx+b,根据题意,得
∴y与x之间的函数关系为y=-60x+180(1.5≤x≤3);
(2)当x=2时,y=-60×2+180=60,
∴乙骑摩托车的速度为60÷2=30(km/h),
∴乙从A地到B地用时为90÷30=3(h).
答:乙从A地到B地用了3 h.
【中考变形】
1.[2016·山西]我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2 000 kg~5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货;
方案B:每千克5元,客户需支付运费2 000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20 000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.
解:(1)方案A:函数表达式为y=5.8x,
方案B:函数表达式为y=5x+2 000;
(2)由题意,得5.8x<5x+2 000,
解得x<2 500.
∴当购买量x的取值范围为2 000≤x<2 500时,选用方案A比方
案B付款少;
(3)他应选择方案B.
2.[2015·济宁]小明到服装店进行社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元,乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
解:(1)设甲种服装购进x件,则乙种服装购进(100-x)件,
解得65≤x≤75,
答:甲种服装最多购进75件;
(2)设总利润为W元,
W=(120-80-a)x+(90-60)×(100-x),
即W=(10-a)x+3 000.
①当0<a<10时,10-a>0,W随x增大而增大,
∴当x=75时,W有最大值,即此时购进甲种服装75件,乙种服装25件;
②当a=10时,在65≤x≤75范围内按任意一种方案进货都可以;
③当10<a<20时,10-a<0,W随x增大而减小.
∴当x=65时,W有最大值,即此时购进甲种服装65件,乙种服装35件.
3.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 乙
进价(元/部) 4 000 2 500
售价(元/部) 4 300 3 000
该商场计划购进两种手机若干部,共需15.5万元,预计全
部销售后可获毛利润共2.1万元[毛利润=(售价-进价)×销售量].
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,才能使全部销售后获得的毛利润最大?并求出最大毛利润.
(2)设甲种手机的购进数量减少a部,则乙种手机的购进数量增加2a部,
由题意,得0.4×(20-a)+0.25×(30+2a)≤16,
解得a≤5.
设全部销售后获得的毛利润为W万元,由题意,得
W=0.03×(20-a)+0.05×(30+2a)
=0.07a+2.1.
∵k=0.07>0,
∴W随a的增大而增大,
∴当a=5时,W最大=2.45万元.
答:该商场购进甲种手机15部,乙种手机40部可使获得的毛利润最大,最大毛利润为2.45万元.
【中考预测】
某商店销售10台A型和20台B型电脑的利润为4 000元,销售20台A型和10台B型电脑的利润为3 500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型,B型电脑各多少台,才能使销售总利润最大?
解:(1)设每台A型电脑销售利润为m元,每台B型电脑的销售
利润为n元,
答:每台A型电脑的销售利润为100元,每台B型电脑的销售
利润为150元;
(2)①据题意,得y=100x+150×(100-x),
即y=-50x+15 000,
②据题意,得100-x≤2x,
∵y=-50x+15 000,
∴y随x的增大而减小,
∵x为正整数,
∴当x=34时,y有最大值,则100-x=66,
答:商店购进34台A型电脑和66台B型电脑时,销售利润最大.
谢 谢
小结
类型之一 一次函数的图象的应用
【教材原型】
____________.
图Z5-1
【思想方法】 (1)每个二元一次方程组都对应着两个一次函数,于是也对应着两条直线.从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线的交点坐标;
(2)一次函数、一元一次方程、一元一次不等式有着独立的概念,但在本质上,后者是前者的特殊情况,从而可以利用函数图象解决方程或方程组问题,体现数形结合思想.
【中考变形】
1.[2015·衢州改编]高铁的开通,给衢州市民出行带来了极大的方便.五一期间,乐乐和颖颖相约到杭州市某游乐园游玩,乐乐乘私家车从衢州出发1 h后,颖颖乘坐高铁从衢州出发,先到杭州火车东站,然后转乘出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(km)与乘车时间t(h)的关系如图Z5-2所示.请结合图象解决下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)当颖颖到达杭州火车东站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18 min到达游乐园,问私家车的速度必须达到
多少千米/小时?
图Z5-2
2.[2016·南充]小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2 500 m,如图Z5-3是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20 min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
(2)设爸爸所走的路程s与时间t的函数关系式为s=kt+b,
图Z5-3
则爸爸所走的路程与步行时间的关系式为s=30t+250,
小明与爸爸第三次相遇应该是t>30 min时,
当50t-500=30t+250,即t=37.5 min时,小明与爸爸第三次相遇;
(3)30t+250=2 500,解得t=75,
则爸爸到达公园需要75 min,
∵小明到达公园需要的时间是60 min,
如果小明希望比爸爸早20 min到达公园,则小明在步行过程中停留的时间需减少5 min.
【中考预测】
甲、乙两人同时从相距90 km的A地前往B
地,甲乘汽车,乙骑摩托车,甲到达B地
停留半个小时后返回A地,如图Z5-5是
他们离A地的距离y(km)与时间x(h)之间的
函数关系图象.
(1)求甲从B地返回A地的过程中,y与x之间
的函数关系式,并写出自变量的取值范围;
(2)若乙出发后2 h和甲相遇,求乙从A地到B地用了多长
时间?
图Z5-5
解:(1)设函数关系式为y=kx+b,根据题意,得
∴y与x之间的函数关系为y=-60x+180(1.5≤x≤3);
(2)当x=2时,y=-60×2+180=60,
∴乙骑摩托车的速度为60÷2=30(km/h),
∴乙从A地到B地用时为90÷30=3(h).
答:乙从A地到B地用了3 h.
【中考变形】
1.[2016·山西]我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2 000 kg~5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货;
方案B:每千克5元,客户需支付运费2 000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20 000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.
解:(1)方案A:函数表达式为y=5.8x,
方案B:函数表达式为y=5x+2 000;
(2)由题意,得5.8x<5x+2 000,
解得x<2 500.
∴当购买量x的取值范围为2 000≤x<2 500时,选用方案A比方
案B付款少;
(3)他应选择方案B.
2.[2015·济宁]小明到服装店进行社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元,乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
解:(1)设甲种服装购进x件,则乙种服装购进(100-x)件,
解得65≤x≤75,
答:甲种服装最多购进75件;
(2)设总利润为W元,
W=(120-80-a)x+(90-60)×(100-x),
即W=(10-a)x+3 000.
①当0<a<10时,10-a>0,W随x增大而增大,
∴当x=75时,W有最大值,即此时购进甲种服装75件,乙种服装25件;
②当a=10时,在65≤x≤75范围内按任意一种方案进货都可以;
③当10<a<20时,10-a<0,W随x增大而减小.
∴当x=65时,W有最大值,即此时购进甲种服装65件,乙种服装35件.
3.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 乙
进价(元/部) 4 000 2 500
售价(元/部) 4 300 3 000
该商场计划购进两种手机若干部,共需15.5万元,预计全
部销售后可获毛利润共2.1万元[毛利润=(售价-进价)×销售量].
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,才能使全部销售后获得的毛利润最大?并求出最大毛利润.
(2)设甲种手机的购进数量减少a部,则乙种手机的购进数量增加2a部,
由题意,得0.4×(20-a)+0.25×(30+2a)≤16,
解得a≤5.
设全部销售后获得的毛利润为W万元,由题意,得
W=0.03×(20-a)+0.05×(30+2a)
=0.07a+2.1.
∵k=0.07>0,
∴W随a的增大而增大,
∴当a=5时,W最大=2.45万元.
答:该商场购进甲种手机15部,乙种手机40部可使获得的毛利润最大,最大毛利润为2.45万元.
【中考预测】
某商店销售10台A型和20台B型电脑的利润为4 000元,销售20台A型和10台B型电脑的利润为3 500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型,B型电脑各多少台,才能使销售总利润最大?
解:(1)设每台A型电脑销售利润为m元,每台B型电脑的销售
利润为n元,
答:每台A型电脑的销售利润为100元,每台B型电脑的销售
利润为150元;
(2)①据题意,得y=100x+150×(100-x),
即y=-50x+15 000,
②据题意,得100-x≤2x,
∵y=-50x+15 000,
∴y随x的增大而减小,
∵x为正整数,
∴当x=34时,y有最大值,则100-x=66,
答:商店购进34台A型电脑和66台B型电脑时,销售利润最大.
谢 谢
