华东师大版八年级下册数学第19章矩形、菱形与正方形复习 课件(共19张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学第19章矩形、菱形与正方形复习 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 425.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 16:01:59 | ||
图片预览


文档简介
(共19张PPT)
复习题
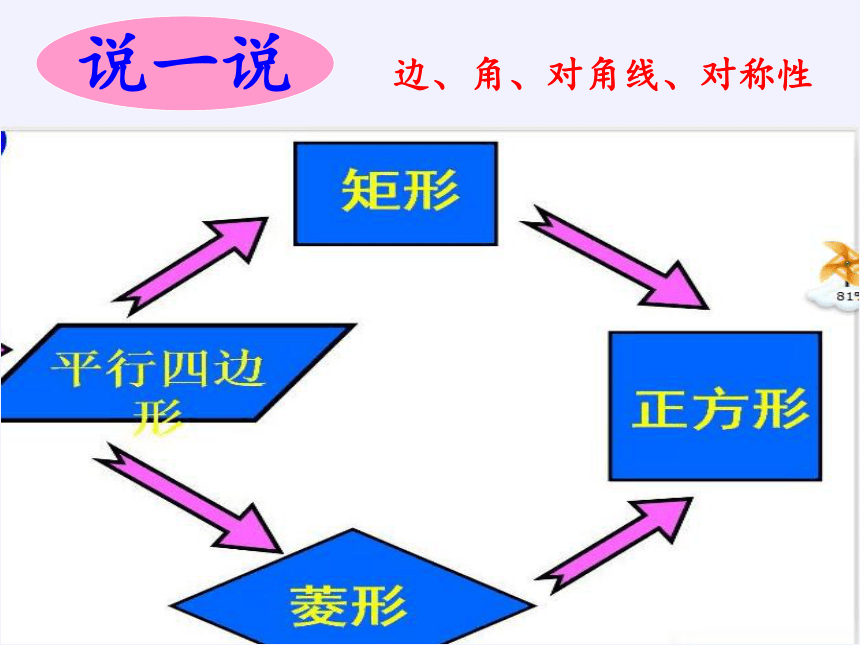
说一说
边、角、对角线、对称性
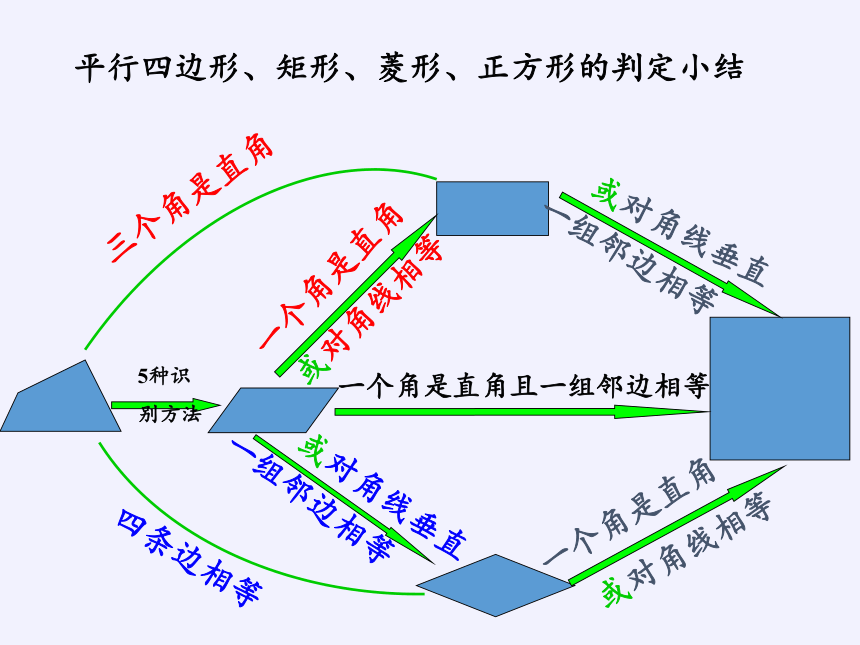
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1、要使 ABCD成为矩形,需增加的条件
是 。
2、要使 ABCD成为菱形,需增加的条件
是 。
3、要使矩形ABCD成为正方形,需增加的条件
是 。
4、要使菱形ABCD成为正方形,需增加的条件
是 。
5、要使四边形ABCD成为正方形,需增加的条件
是 。
抢答
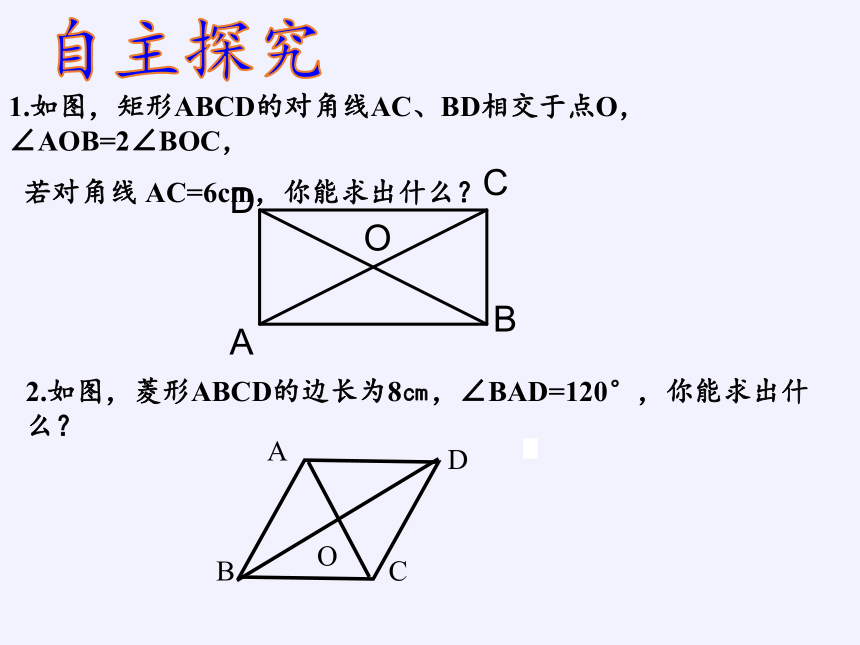
1.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=2∠BOC,
若对角线 AC=6cm,你能求出什么?
2.如图,菱形ABCD的边长为8㎝,∠BAD=120°,你能求出什么?
A
B
C
D
O
自主探究
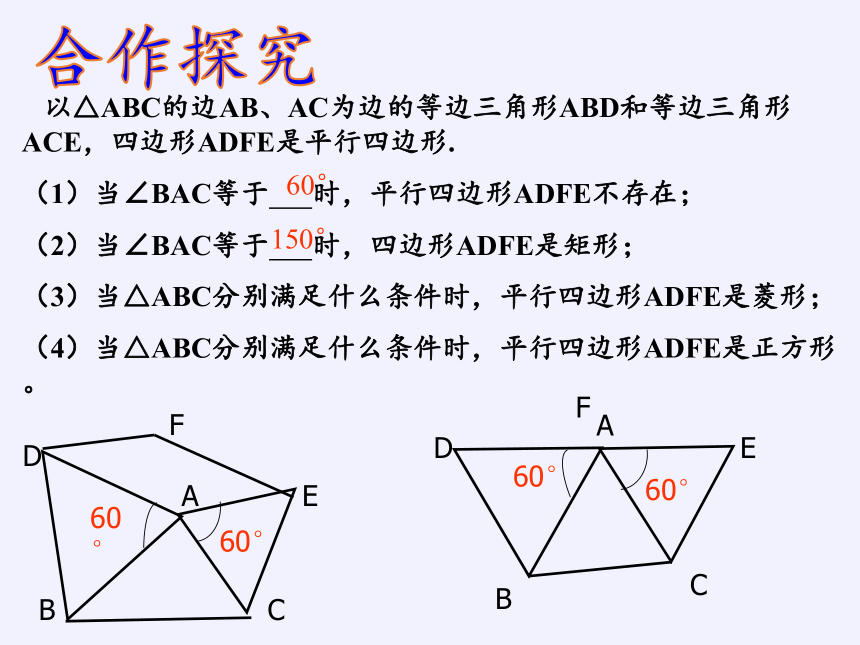
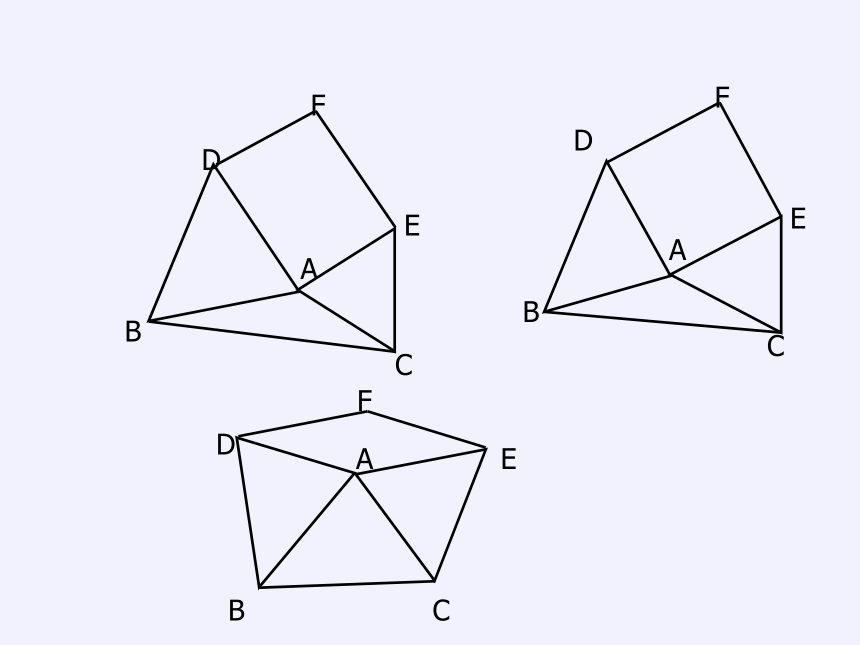
以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC等于 时,平行四边形ADFE不存在;
(2)当∠BAC等于 时,四边形ADFE是矩形;
(3)当△ABC分别满足什么条件时,平行四边形ADFE是菱形;
(4)当△ABC分别满足什么条件时,平行四边形ADFE是正方形。
60°
150°
合作探究
B
C
A
E
F
D
60°
60°
60°
60°
B
C
A
E
F
D
B
C
A
E
F
D
B
C
A
E
F
D
B
C
A
E
F
D
如图,在Rt△ABC中,∠ACB=90 ,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形 说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形 请说明你的理由。
(1)证明:∵DE⊥BC,
∴∠DFB=90 ,
∵∠ACB=90 ,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
练一练
(2)四边形BECD是菱形,
理由是:∵D为AB中点
∴AD=BD
∵CE=AD
∴BD=CE
∵BD∥CE
∴四边形BECD是平行四边形,
∵∠ACB=90 ,D为AB中点,
∴CD=BD
∴ 四边形BECD是菱形;
(3)当∠A=45 时,四边形BECD是正方形,
理由是:
∵∠ACB=90 ,∠A=45
∴∠ABC=∠A=45
∴AC=BC,
∵D为BA中点
∴CD⊥AB,
∴∠CDB=90
∵四边形BECD是菱形
∴菱形BECD是正方形
即当∠A=45 时,四边形BECD是正方形
1、顺次连接任意四边形各边的中点,
所构成的四边形简称“中点四边形”
那么特殊平行四边形的“中点四边形”会是怎样的图形呢?
拓展1
O
我发现:
顺次连接任意的四边形各边中点得
顺次连接对角线相等的四边形各边中点得
顺次连接对角线互相垂直的四边形各边中点得
顺次连接对角线相等且互相垂直的四边形各边中点得
平行四边形;
菱形;
矩形;
正方形.
2、如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=4,OC=2,求出经过点E的反比例函数解析式.
拓展2
N
H
M
3、如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
拓展3
3
F`
课堂小结
通过本节课的学习,你有哪 些收获?
课 堂 小 结
1、请理解并熟记特殊平行四边形的性质和
判定.
2、在解题时,
首先,应有战胜困难的决心和信心;
其次,抓住图形中的位置关系与条件中
的数量关系;
再次,注意每一个判断都应有充分的理
由和依据.
送给同学们一句话:
相信自己,学好数学并不难!
1、检查一个门框是矩形的方法是( )
A、测量两条对角线是否相等.
B、测量有三个角是直角.
C、量两条对角线是否互相平分.
D、 测量两条对角线是否互相垂直.
2、顺次连接矩形各边中点所得的四边形是( )
A、矩形 B、菱形 C、梯形 D、正方形
B
B
挑战自我
3、菱形的周长等于高的8倍,则其最大内角 等于( ) A、60° B、90° C、120° D、150°
4、矩形ABCD中,AB=8,BC=6,E、F是AC的三等分点,则△BEF的面积是( )
A、8 B、12 C、16 D、24
D
D
A
C
B
E
F
A
E
A
D
C
B
∟
5、在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到_____________
A
B
C
D
E
F
G
P
谢 谢
复习题
说一说
边、角、对角线、对称性
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1、要使 ABCD成为矩形,需增加的条件
是 。
2、要使 ABCD成为菱形,需增加的条件
是 。
3、要使矩形ABCD成为正方形,需增加的条件
是 。
4、要使菱形ABCD成为正方形,需增加的条件
是 。
5、要使四边形ABCD成为正方形,需增加的条件
是 。
抢答
1.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=2∠BOC,
若对角线 AC=6cm,你能求出什么?
2.如图,菱形ABCD的边长为8㎝,∠BAD=120°,你能求出什么?
A
B
C
D
O
自主探究
以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC等于 时,平行四边形ADFE不存在;
(2)当∠BAC等于 时,四边形ADFE是矩形;
(3)当△ABC分别满足什么条件时,平行四边形ADFE是菱形;
(4)当△ABC分别满足什么条件时,平行四边形ADFE是正方形。
60°
150°
合作探究
B
C
A
E
F
D
60°
60°
60°
60°
B
C
A
E
F
D
B
C
A
E
F
D
B
C
A
E
F
D
B
C
A
E
F
D
如图,在Rt△ABC中,∠ACB=90 ,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形 说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形 请说明你的理由。
(1)证明:∵DE⊥BC,
∴∠DFB=90 ,
∵∠ACB=90 ,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
练一练
(2)四边形BECD是菱形,
理由是:∵D为AB中点
∴AD=BD
∵CE=AD
∴BD=CE
∵BD∥CE
∴四边形BECD是平行四边形,
∵∠ACB=90 ,D为AB中点,
∴CD=BD
∴ 四边形BECD是菱形;
(3)当∠A=45 时,四边形BECD是正方形,
理由是:
∵∠ACB=90 ,∠A=45
∴∠ABC=∠A=45
∴AC=BC,
∵D为BA中点
∴CD⊥AB,
∴∠CDB=90
∵四边形BECD是菱形
∴菱形BECD是正方形
即当∠A=45 时,四边形BECD是正方形
1、顺次连接任意四边形各边的中点,
所构成的四边形简称“中点四边形”
那么特殊平行四边形的“中点四边形”会是怎样的图形呢?
拓展1
O
我发现:
顺次连接任意的四边形各边中点得
顺次连接对角线相等的四边形各边中点得
顺次连接对角线互相垂直的四边形各边中点得
顺次连接对角线相等且互相垂直的四边形各边中点得
平行四边形;
菱形;
矩形;
正方形.
2、如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=4,OC=2,求出经过点E的反比例函数解析式.
拓展2
N
H
M
3、如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
拓展3
3
F`
课堂小结
通过本节课的学习,你有哪 些收获?
课 堂 小 结
1、请理解并熟记特殊平行四边形的性质和
判定.
2、在解题时,
首先,应有战胜困难的决心和信心;
其次,抓住图形中的位置关系与条件中
的数量关系;
再次,注意每一个判断都应有充分的理
由和依据.
送给同学们一句话:
相信自己,学好数学并不难!
1、检查一个门框是矩形的方法是( )
A、测量两条对角线是否相等.
B、测量有三个角是直角.
C、量两条对角线是否互相平分.
D、 测量两条对角线是否互相垂直.
2、顺次连接矩形各边中点所得的四边形是( )
A、矩形 B、菱形 C、梯形 D、正方形
B
B
挑战自我
3、菱形的周长等于高的8倍,则其最大内角 等于( ) A、60° B、90° C、120° D、150°
4、矩形ABCD中,AB=8,BC=6,E、F是AC的三等分点,则△BEF的面积是( )
A、8 B、12 C、16 D、24
D
D
A
C
B
E
F
A
E
A
D
C
B
∟
5、在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到_____________
A
B
C
D
E
F
G
P
谢 谢
