华东师大版七年级下册数学 9.1.2 三角形的内角和 教案
文档属性
| 名称 | 华东师大版七年级下册数学 9.1.2 三角形的内角和 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 104.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览

文档简介
第9章 多边形
9.1.2三角形的内角和
【教学目标】
知识与技能:
1.使学生在操作活动中,探索并了解三角形的内角和、直角三角形两个锐角互余.
2.能利用三角形内角和进行有关计算.
过程与方法:
在学生学习内角和性质的推导过程中,使学生学会探索数学问题的归纳法和实验法等研究方法。
情感、态度与价值观:
1.体会一切理论来源于实践,又返回来服务于实际生活的思想。
2.体会一切事物既存在着一定的联系,又有一定的区别。只有弄清它们的本质,才能更好地为人类服务。
3.不等关系是实际生活中最多的数量关系,通过这节课的学习使学生感到我也会研究数学,增强学好不等式的信心。
【教学重点】
掌握三角形的内角和、外角和以及外角的性质.
【教学难点】
在性质证明的过程中,涉及到添加辅助线来沟通证明思路的方法.
【教学过程】
活动引入:你有什么办法可以探究它呢
验证三角形内角和定理1.
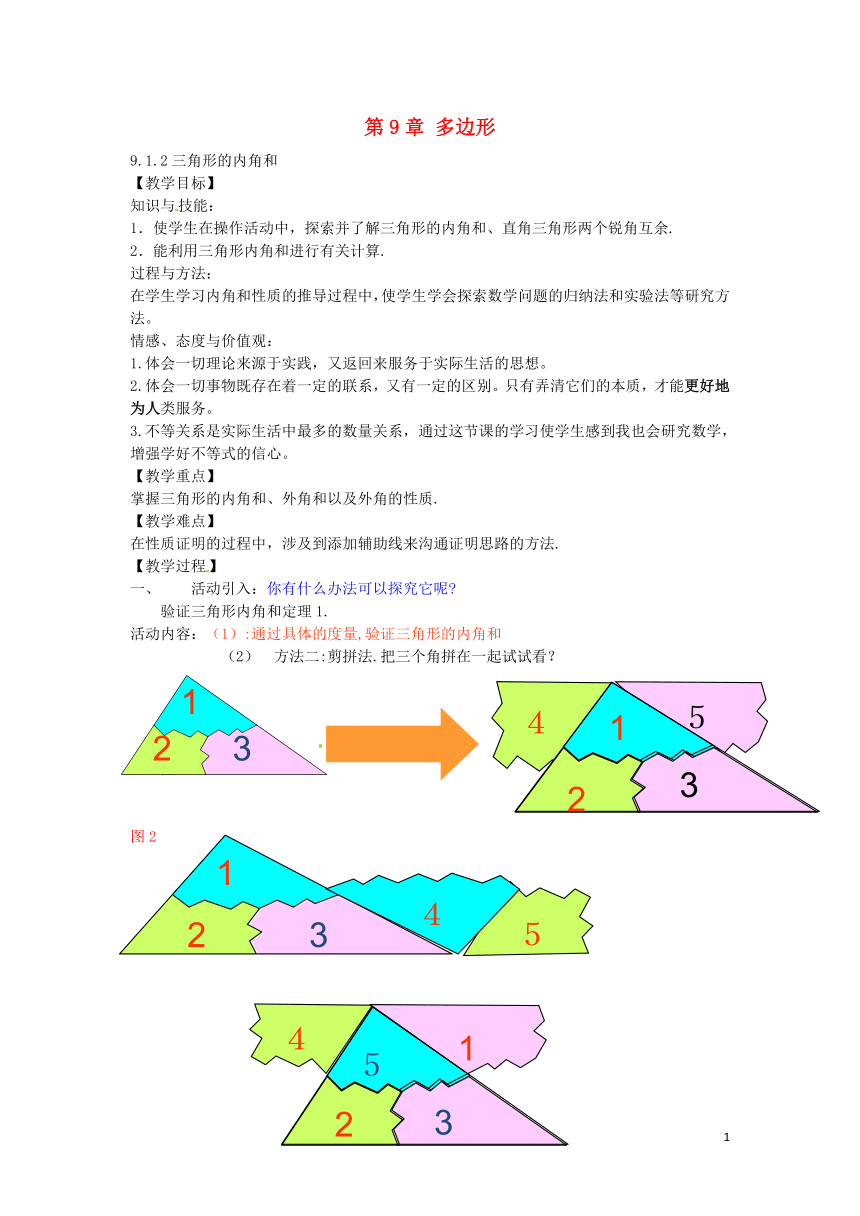
活动内容:(1):通过具体的度量,验证三角形的内角和
(
1
) (2) 方法二:剪拼法.把三个角拼在一起试试看?
(
4
) (
5
) (
1
) (
3
) (
2
)
(
2
) (
3
)
图1
(
1
)
图2
(
4
)
(
5
) (
2
) (
3
)
(
1
2
5
4
)
(
3
)
通过测量发现三角形的三个内角和是180°从刚才拼角的过程你能想出证明的方法吗
已知:△ABC. 求证:∠A +∠B +∠C =180°
证明:如图,过A作EF∥BC
∴∠2=∠4(两直线平行,内错角相等)
同理:∠3=∠5(两直线平行,内错角相等)
∵∠4+∠1+∠5=180° (平角定义)
∴∠1+∠2+∠3=180°(等量代换)
(
A
B
C
D
E
) (
A
B
C
E
D
)2、
方法一:过A点作DE∥BC
∵DE∥BC
∴∠DAB=∠B,∠EAC=∠C(两直线平行,内错角相等)
∵∠DAB+∠BAC+∠EAC=180°
∴∠BAC+∠B+∠C=180°(等量代换)
方法二:作BC的延长线CD,过点C作射线CE∥BA.
∵CE∥BA
∴∠B=∠ECD(两直线平行,同位角相等)
∠A=∠ACE(两直线平行,内错角相等)
∵∠BCA+∠ACE+∠ECD=180°
∴∠A+∠B+∠ACB=180°(等量代换)
2.直角三角形两锐角之间的关系
由三角形的内角和等于180°,容易得到下面的结论:
直角三角形的两个锐角互余.
新知应用:比一比,赛一赛
(1)在△ABC中,∠A=35°,∠ B=43 ° ,
则∠ C=____ 102 °
(2) 在△ABC中,∠C +∠B =140°则∠A=_40 °
(3)在△ABC中, ∠A=40 ° ∠A=2∠B,
则∠C=120°。
二、知识应用
例1如图,D是△ABC的边BC上一点,∠B=∠BAD, ∠ADC=80 , ∠BAC=70 . 求:
(1) ∠ B的度数;
(2) ∠ C的度数.
解:(1)∵ ∠ADC是⊿ABD的外角 (已知)
∴∠ADC=∠B+∠BAD=80
(三角形的一 个外角等于与它不相邻的两个内角的和)
又∵ ∠B=∠BAD(已知)
∴∠B=40°(等量代换)
(2)∵∠ B+ ∠ BAC+ ∠ C= 180 (三角形的内角和为180 )
∴∠ C= 180 - ∠ B - ∠ BAC (等式的性质)
= 180 -40 -70
=70
三、知识梳理
三角形的内角和是多少?
四、随堂练习
教科书课后练习1、2、3
2
9.1.2三角形的内角和
【教学目标】
知识与技能:
1.使学生在操作活动中,探索并了解三角形的内角和、直角三角形两个锐角互余.
2.能利用三角形内角和进行有关计算.
过程与方法:
在学生学习内角和性质的推导过程中,使学生学会探索数学问题的归纳法和实验法等研究方法。
情感、态度与价值观:
1.体会一切理论来源于实践,又返回来服务于实际生活的思想。
2.体会一切事物既存在着一定的联系,又有一定的区别。只有弄清它们的本质,才能更好地为人类服务。
3.不等关系是实际生活中最多的数量关系,通过这节课的学习使学生感到我也会研究数学,增强学好不等式的信心。
【教学重点】
掌握三角形的内角和、外角和以及外角的性质.
【教学难点】
在性质证明的过程中,涉及到添加辅助线来沟通证明思路的方法.
【教学过程】
活动引入:你有什么办法可以探究它呢
验证三角形内角和定理1.
活动内容:(1):通过具体的度量,验证三角形的内角和
(
1
) (2) 方法二:剪拼法.把三个角拼在一起试试看?
(
4
) (
5
) (
1
) (
3
) (
2
)
(
2
) (
3
)
图1
(
1
)
图2
(
4
)
(
5
) (
2
) (
3
)
(
1
2
5
4
)
(
3
)
通过测量发现三角形的三个内角和是180°从刚才拼角的过程你能想出证明的方法吗
已知:△ABC. 求证:∠A +∠B +∠C =180°
证明:如图,过A作EF∥BC
∴∠2=∠4(两直线平行,内错角相等)
同理:∠3=∠5(两直线平行,内错角相等)
∵∠4+∠1+∠5=180° (平角定义)
∴∠1+∠2+∠3=180°(等量代换)
(
A
B
C
D
E
) (
A
B
C
E
D
)2、
方法一:过A点作DE∥BC
∵DE∥BC
∴∠DAB=∠B,∠EAC=∠C(两直线平行,内错角相等)
∵∠DAB+∠BAC+∠EAC=180°
∴∠BAC+∠B+∠C=180°(等量代换)
方法二:作BC的延长线CD,过点C作射线CE∥BA.
∵CE∥BA
∴∠B=∠ECD(两直线平行,同位角相等)
∠A=∠ACE(两直线平行,内错角相等)
∵∠BCA+∠ACE+∠ECD=180°
∴∠A+∠B+∠ACB=180°(等量代换)
2.直角三角形两锐角之间的关系
由三角形的内角和等于180°,容易得到下面的结论:
直角三角形的两个锐角互余.
新知应用:比一比,赛一赛
(1)在△ABC中,∠A=35°,∠ B=43 ° ,
则∠ C=____ 102 °
(2) 在△ABC中,∠C +∠B =140°则∠A=_40 °
(3)在△ABC中, ∠A=40 ° ∠A=2∠B,
则∠C=120°。
二、知识应用
例1如图,D是△ABC的边BC上一点,∠B=∠BAD, ∠ADC=80 , ∠BAC=70 . 求:
(1) ∠ B的度数;
(2) ∠ C的度数.
解:(1)∵ ∠ADC是⊿ABD的外角 (已知)
∴∠ADC=∠B+∠BAD=80
(三角形的一 个外角等于与它不相邻的两个内角的和)
又∵ ∠B=∠BAD(已知)
∴∠B=40°(等量代换)
(2)∵∠ B+ ∠ BAC+ ∠ C= 180 (三角形的内角和为180 )
∴∠ C= 180 - ∠ B - ∠ BAC (等式的性质)
= 180 -40 -70
=70
三、知识梳理
三角形的内角和是多少?
四、随堂练习
教科书课后练习1、2、3
2
