华东师大版七年级下册数学 8.3 一元一次不等式组 课件(共13张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 8.3 一元一次不等式组 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
1.什么叫一元一次不等式组
怎样解一元一次不等式组
2.试一试:
答:_-6____
已知不等式组 的
解集为-1<x<1,则(a+1)(b-1)的值为多少
若 ︱ x ︱=2,则x=
若︱ x ︱<2,则x
若︱4 x ︱ <8, 则x
若︱4 x-3 ︱ <2,则x
±2
-2 < x < 2
-2 < x < 2
由题意得:-2 < 4x -3< 2
4x-3 < 2
4x-3>-2
2、一群女生住若干间宿舍,
每间住4人,剩19人无房住;每
间住6人,有一间宿舍住不满,
(1)设有x间宿舍,请写出x应满足的不等式组;
(2)可能有多少间宿舍,多少名学生
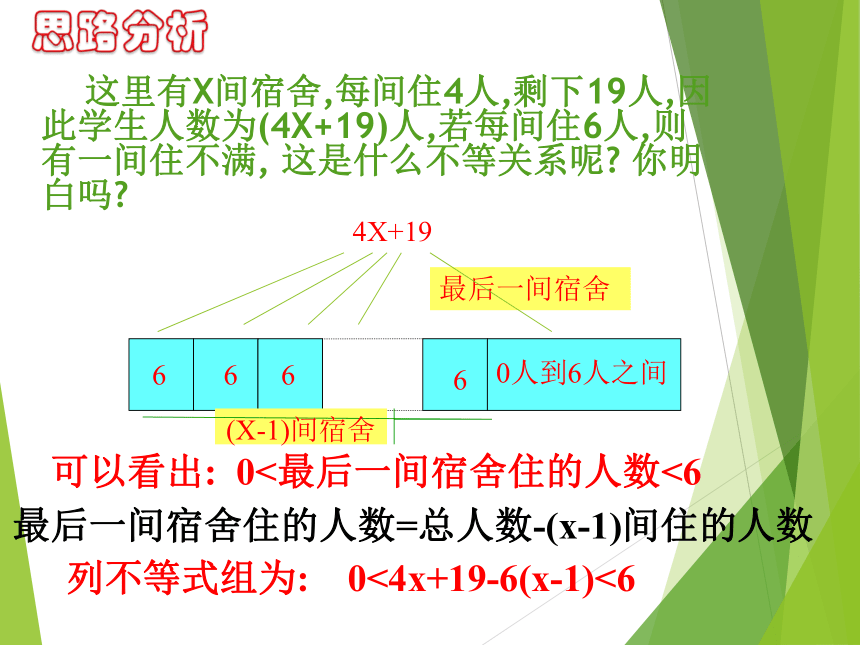
这里有X间宿舍,每间住4人,剩下19人,因此学生人数为(4X+19)人,若每间住6人,则有一间住不满, 这是什么不等关系呢 你明白吗
6
6
6
4X+19
0人到6人之间
最后一间宿舍
6
(X-1)间宿舍
列不等式组为: 0<4x+19-6(x-1)<6
可以看出: 0<最后一间宿舍住的人数<6
最后一间宿舍住的人数=总人数-(x-1)间住的人数
解: 设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
即: 4x+19-6(x-1)>0
4x+19-6(x-1)<6
解得: 18.5因为x是整数,所以x=10,11,12
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生。
实践应用,合作探索
例2: 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
思路分析:
(1)本题的不等关系是:
生产A、B两种产品所需的甲种原料≤360
生产A、B两种产品所需的乙种原料≤290
甲种 乙种
A一件 9 3
Ax件 9x 3x
B一件 4 10
Bx件 4(50-x) 10(50-x)
A、B共需 9x+ 4(50-x) 3x+10(50-x)
(2) 列表看各量的关系
9x+4(50-X)≤360
3x+10(50-x)≤290
所以,列不等式组为:
9x+4(50-X)≤360
3x+10(50-x)≤290
解得:30≤X≤32
所以,可有三种生产方案:A种30件,B种20件;A种31件,B种19件;A种32件,B种18件。
因为x为正整数,所以,X的可能取值为30,31,32
1、有堆苹果分给一组小朋友,如果每人5个,还有18个多余,如果每人7个,则还有一位小朋友分不到7个,求苹果的个数和小朋友的人数。
解:设小朋友人数为x人,则苹果数为(5x+18)个,根据题意得:
解得:9所以x=10、11、12
答:小朋友有10、11或12人,苹果有68、73或78人。
因为x为正整数
1、小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端;体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端。这时,爸爸的一端仍然着地。后来,小宝借来一副质量为6千克的哑铃加在他和妈妈坐的一端,结果,爸爸被跷起离地。猜猜小宝的体重约是多少?
这节课我们学习了构建不等式组的数学模型解决实际问题的数学方法,我们利用不等式组解决实际问题的关键是找出题中的不等关系。
小结
1.什么叫一元一次不等式组
怎样解一元一次不等式组
2.试一试:
答:_-6____
已知不等式组 的
解集为-1<x<1,则(a+1)(b-1)的值为多少
若 ︱ x ︱=2,则x=
若︱ x ︱<2,则x
若︱4 x ︱ <8, 则x
若︱4 x-3 ︱ <2,则x
±2
-2 < x < 2
-2 < x < 2
由题意得:-2 < 4x -3< 2
4x-3 < 2
4x-3>-2
2、一群女生住若干间宿舍,
每间住4人,剩19人无房住;每
间住6人,有一间宿舍住不满,
(1)设有x间宿舍,请写出x应满足的不等式组;
(2)可能有多少间宿舍,多少名学生
这里有X间宿舍,每间住4人,剩下19人,因此学生人数为(4X+19)人,若每间住6人,则有一间住不满, 这是什么不等关系呢 你明白吗
6
6
6
4X+19
0人到6人之间
最后一间宿舍
6
(X-1)间宿舍
列不等式组为: 0<4x+19-6(x-1)<6
可以看出: 0<最后一间宿舍住的人数<6
最后一间宿舍住的人数=总人数-(x-1)间住的人数
解: 设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
即: 4x+19-6(x-1)>0
4x+19-6(x-1)<6
解得: 18.5
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生。
实践应用,合作探索
例2: 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
思路分析:
(1)本题的不等关系是:
生产A、B两种产品所需的甲种原料≤360
生产A、B两种产品所需的乙种原料≤290
甲种 乙种
A一件 9 3
Ax件 9x 3x
B一件 4 10
Bx件 4(50-x) 10(50-x)
A、B共需 9x+ 4(50-x) 3x+10(50-x)
(2) 列表看各量的关系
9x+4(50-X)≤360
3x+10(50-x)≤290
所以,列不等式组为:
9x+4(50-X)≤360
3x+10(50-x)≤290
解得:30≤X≤32
所以,可有三种生产方案:A种30件,B种20件;A种31件,B种19件;A种32件,B种18件。
因为x为正整数,所以,X的可能取值为30,31,32
1、有堆苹果分给一组小朋友,如果每人5个,还有18个多余,如果每人7个,则还有一位小朋友分不到7个,求苹果的个数和小朋友的人数。
解:设小朋友人数为x人,则苹果数为(5x+18)个,根据题意得:
解得:9
答:小朋友有10、11或12人,苹果有68、73或78人。
因为x为正整数
1、小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端;体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端。这时,爸爸的一端仍然着地。后来,小宝借来一副质量为6千克的哑铃加在他和妈妈坐的一端,结果,爸爸被跷起离地。猜猜小宝的体重约是多少?
这节课我们学习了构建不等式组的数学模型解决实际问题的数学方法,我们利用不等式组解决实际问题的关键是找出题中的不等关系。
小结
