2021-2022学年华东师大版数学七年级下册6.2.2解一元一次方程课件(第三课时 17张)
文档属性
| 名称 | 2021-2022学年华东师大版数学七年级下册6.2.2解一元一次方程课件(第三课时 17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 23:51:57 | ||
图片预览





文档简介
(共17张PPT)
6.2.2 一元一次方程的简单应用
复习旧知
01
情境引入
02
知识归纳
03
尝试运用
04
CONTENTS
目录
课堂小结
05
一、复习旧知
将方程去分母得到.错在( )
A.分母的最小公倍数找错
B.去分母时,漏乘了分母为1的项
C.去分母时,分子部分没有加括号
D.去分母时,各项所乘的数不同
去分母解方程
C
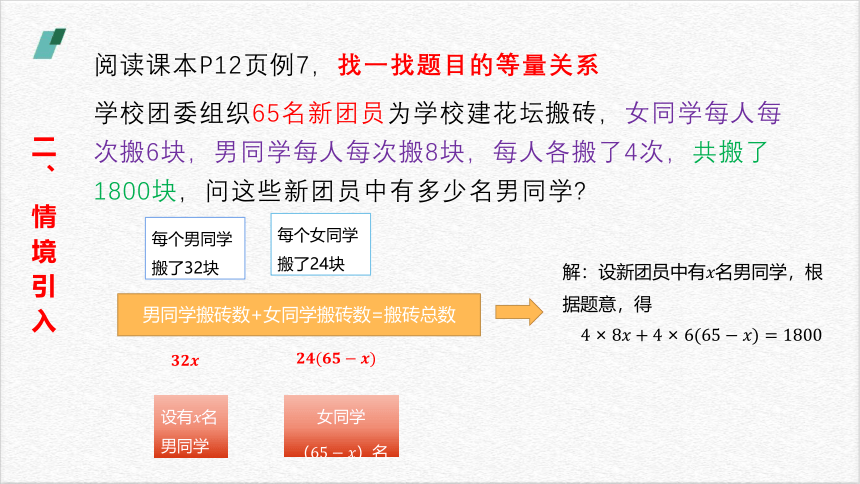
阅读课本P12页例7,找一找题目的等量关系
学校团委组织65名新团员为学校建花坛搬砖,女同学每人每次搬6块,男同学每人每次搬8块,每人各搬了4次,共搬了1800块,问这些新团员中有多少名男同学
二、情境引入
男同学搬砖数+女同学搬砖数=搬砖总数
解:设新团员中有名男同学,根据题意,得
每个男同学搬了32块
每个女同学搬了24块
设有名男同学
女同学
名
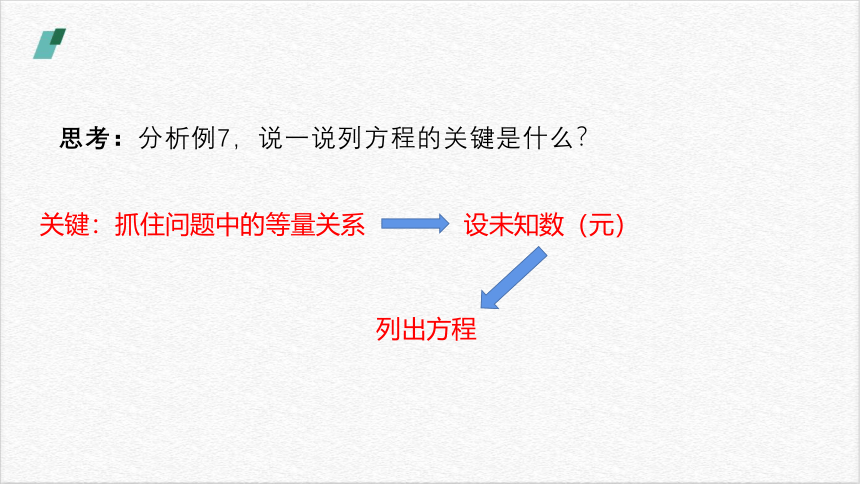
思考:分析例7,说一说列方程的关键是什么?
关键:抓住问题中的等量关系
设未知数(元)
列出方程
基础练习
(1)2与25的和等于20,列得方程为 ;
(2)的3倍减去10等于35,列得方程为 ;;
找等量关系,列方程
提高练习
(3)某数的3倍减去9,等于该数的三分之一加上6,
根据题意列出方程为 ;
(4)已知代数式与代数式的值互为相反数,根据题意列出方程 ;
找等量关系,列方程
答案:
答案:
根据例7,说一说列出方程后的步骤
学校团委组织65名新团员为学校建花坛搬砖,女同学每人每次搬6块,男同学每人每次搬8块,每人各搬了4次,共搬了1800块,问这些新团员中有多少名男同学
三、知识归纳
解:设新团员中有名男同学,根据题意,得
解得
经检验,符合题意.
答:这些新团员有30名男同学
列出方程
求得方程的解后
经过检验
得到实际问题的解(答)
知识小结
一元一次方程解决实际问题的步骤
抓住问题中的等量关系
列出方程
求得方程的解后
经过检验
得到实际问题的解(答)
基本步骤:
“审”、“设”、“找”、“列”、“解”、“验”、“答”
四、尝试运用
1.买4本练习本与3支铅笔一共用了 2.3元,已知铅笔每支0.5元,则练习本每本多少元
等量关系:练习本的总价+铅笔的总价=一共用的钱
解:设练习本每本元,根据题意可得:
解得:
经检验,符合题意.
答:练习本每本0.2元
设练习本每本元
4
2.小红今年6岁,她的祖父72岁,几年后,小红的年龄是她祖父年龄的
等量关系:小红的年龄=她祖父年龄
解:设年后,小红的年龄是她祖父年龄的, 根据题意可得:
解得:
经检验,符合题意.
答:年后小红的年龄是她祖父年龄的
设年后
点睛:一般求什么,就把什么设为元
五、课堂小结
弄清题意和其中的数量关系,用字母表示适当的未知数(设元);
问题
方程
解答
列方程解决实际问题的步骤:
审”、“设”、“找”、“列”
“解” 、“验”、“答”
特别注意:在设未知数和作出解答时,应注意量的单位.
如何设未知数?
在设未知数时,一般有以下几种情况:
①一般情况下题目问什么设什么,即设直接未知数;
②特殊情况下,可以设另外一个相关未知量为未知数;
③在某些情况下为了便于列方程,可以设辅助未知数。
“审”、“设”、“找”、“列”、“解”、“验”、“答”
基础练习
1、把若干本书发给学生。如果每人发4本,那么还剩下25木;如果每人发5本,那么还差5本.问学生有多少人·
解:设学生有,根据题意,得:
解得:
经检验,符合题意.
答:学生有人
基础练习
2、某商品的进价是100元,按商品标价的八折出售时,利润率是12%,问商品标价为多少元
解:设商品标价为元,根据题意,得:
解得:
经检验,符合题意.
答:商品标价为元
知识点睛:售价进价=利润
标价折扣=售价
利润进价=利润率
提高练习
学校田径队的小刚在400米跑测试时,先以6来/秒的平均速度跑了大部分路程,最后以8米/秒的这度冲刺到达终点,成绩为1分零5秒.问小刚在冲刺阶段花了多少时间
解:设小刚冲刺阶段花了秒,根据题意,得:
解得:
经检验,符合题意.
答:小刚在冲刺阶段花了5秒钟
特别注意:在设未知数和作出解答时,应注意量的单位.
链接中考
(2021四川南充中考)端午节买粽子, 每个肉粽比每个素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽元,
则可列方程为 ;
6.2.2 一元一次方程的简单应用
复习旧知
01
情境引入
02
知识归纳
03
尝试运用
04
CONTENTS
目录
课堂小结
05
一、复习旧知
将方程去分母得到.错在( )
A.分母的最小公倍数找错
B.去分母时,漏乘了分母为1的项
C.去分母时,分子部分没有加括号
D.去分母时,各项所乘的数不同
去分母解方程
C
阅读课本P12页例7,找一找题目的等量关系
学校团委组织65名新团员为学校建花坛搬砖,女同学每人每次搬6块,男同学每人每次搬8块,每人各搬了4次,共搬了1800块,问这些新团员中有多少名男同学
二、情境引入
男同学搬砖数+女同学搬砖数=搬砖总数
解:设新团员中有名男同学,根据题意,得
每个男同学搬了32块
每个女同学搬了24块
设有名男同学
女同学
名
思考:分析例7,说一说列方程的关键是什么?
关键:抓住问题中的等量关系
设未知数(元)
列出方程
基础练习
(1)2与25的和等于20,列得方程为 ;
(2)的3倍减去10等于35,列得方程为 ;;
找等量关系,列方程
提高练习
(3)某数的3倍减去9,等于该数的三分之一加上6,
根据题意列出方程为 ;
(4)已知代数式与代数式的值互为相反数,根据题意列出方程 ;
找等量关系,列方程
答案:
答案:
根据例7,说一说列出方程后的步骤
学校团委组织65名新团员为学校建花坛搬砖,女同学每人每次搬6块,男同学每人每次搬8块,每人各搬了4次,共搬了1800块,问这些新团员中有多少名男同学
三、知识归纳
解:设新团员中有名男同学,根据题意,得
解得
经检验,符合题意.
答:这些新团员有30名男同学
列出方程
求得方程的解后
经过检验
得到实际问题的解(答)
知识小结
一元一次方程解决实际问题的步骤
抓住问题中的等量关系
列出方程
求得方程的解后
经过检验
得到实际问题的解(答)
基本步骤:
“审”、“设”、“找”、“列”、“解”、“验”、“答”
四、尝试运用
1.买4本练习本与3支铅笔一共用了 2.3元,已知铅笔每支0.5元,则练习本每本多少元
等量关系:练习本的总价+铅笔的总价=一共用的钱
解:设练习本每本元,根据题意可得:
解得:
经检验,符合题意.
答:练习本每本0.2元
设练习本每本元
4
2.小红今年6岁,她的祖父72岁,几年后,小红的年龄是她祖父年龄的
等量关系:小红的年龄=她祖父年龄
解:设年后,小红的年龄是她祖父年龄的, 根据题意可得:
解得:
经检验,符合题意.
答:年后小红的年龄是她祖父年龄的
设年后
点睛:一般求什么,就把什么设为元
五、课堂小结
弄清题意和其中的数量关系,用字母表示适当的未知数(设元);
问题
方程
解答
列方程解决实际问题的步骤:
审”、“设”、“找”、“列”
“解” 、“验”、“答”
特别注意:在设未知数和作出解答时,应注意量的单位.
如何设未知数?
在设未知数时,一般有以下几种情况:
①一般情况下题目问什么设什么,即设直接未知数;
②特殊情况下,可以设另外一个相关未知量为未知数;
③在某些情况下为了便于列方程,可以设辅助未知数。
“审”、“设”、“找”、“列”、“解”、“验”、“答”
基础练习
1、把若干本书发给学生。如果每人发4本,那么还剩下25木;如果每人发5本,那么还差5本.问学生有多少人·
解:设学生有,根据题意,得:
解得:
经检验,符合题意.
答:学生有人
基础练习
2、某商品的进价是100元,按商品标价的八折出售时,利润率是12%,问商品标价为多少元
解:设商品标价为元,根据题意,得:
解得:
经检验,符合题意.
答:商品标价为元
知识点睛:售价进价=利润
标价折扣=售价
利润进价=利润率
提高练习
学校田径队的小刚在400米跑测试时,先以6来/秒的平均速度跑了大部分路程,最后以8米/秒的这度冲刺到达终点,成绩为1分零5秒.问小刚在冲刺阶段花了多少时间
解:设小刚冲刺阶段花了秒,根据题意,得:
解得:
经检验,符合题意.
答:小刚在冲刺阶段花了5秒钟
特别注意:在设未知数和作出解答时,应注意量的单位.
链接中考
(2021四川南充中考)端午节买粽子, 每个肉粽比每个素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽元,
则可列方程为 ;
