2021-2022学年北师大版七年级数学下册2.1.1两条直线间的关系课件(26张)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册2.1.1两条直线间的关系课件(26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 23:53:41 | ||
图片预览





文档简介
(共26张PPT)
2.1.1两条直线间的关系
公园一角,
亭台楼阁
整齐的自行车棚
漂亮的小木栅栏
想一想:上述图片中的两条直线有哪几种位置关系?
若两条直线只有一个公共点,我们称这两条直线为相交线。
在同一平面内,不相交的两条直线叫做平行线。
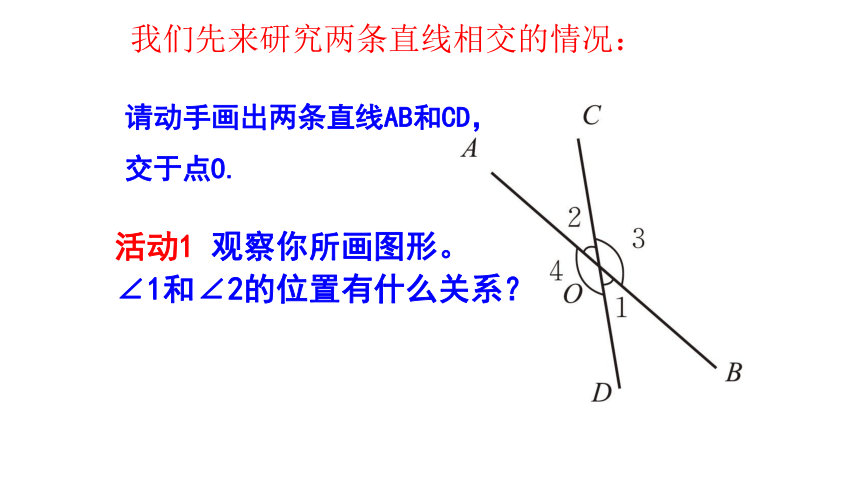
请动手画出两条直线AB和CD,
交于点O.
活动1 观察你所画图形。
∠1和∠2的位置有什么关系?
我们先来研究两条直线相交的情况:
1
2
1
2
1
2
1
2
A
B
C
D
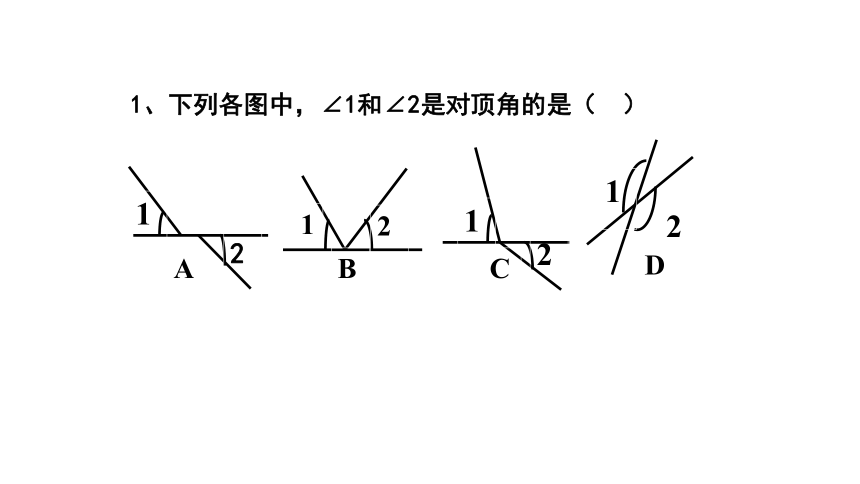
1、下列各图中,∠1和∠2是对顶角的是( )
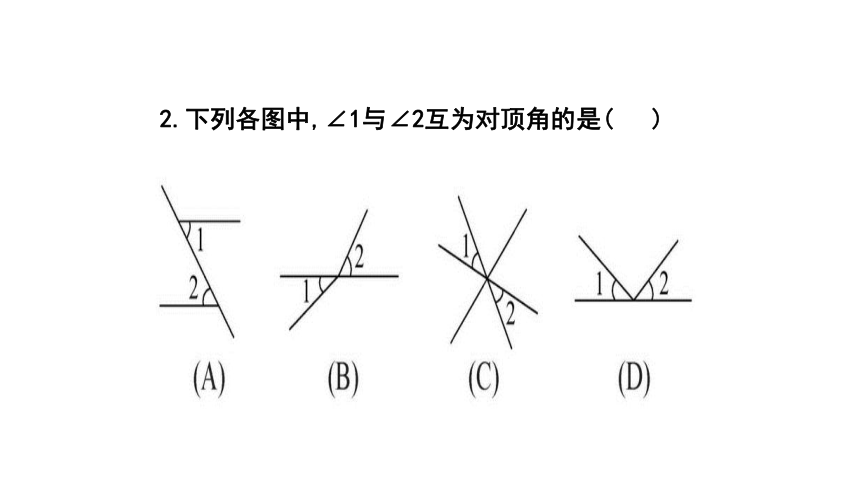
2.下列各图中,∠1与∠2互为对顶角的是( )
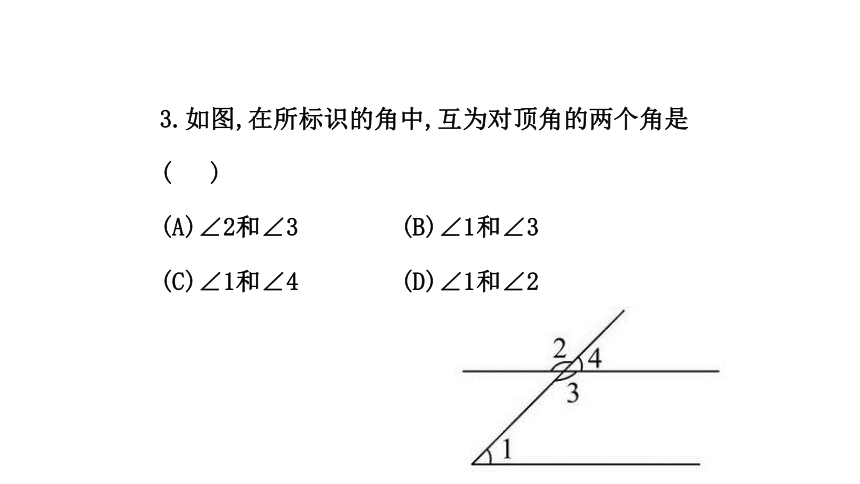
3.如图,在所标识的角中,互为对顶角的两个角是( )
(A)∠2和∠3 (B)∠1和∠3
(C)∠1和∠4 (D)∠1和∠2
找出对顶角
A
B
C
D
E
F
O
活动2:任意一组对顶角大小有何关系?
∵直线AB与CD相交于点O
对顶角相等
3
2
1
4
A
B
C
D
o
∴ ∠1=∠2, ∠3=∠4 (对顶角相等)
文字语言:
几何语言:
联系生活
有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
3
2
1
4
A
B
C
D
o
3
2
1
4
A
B
C
D
o
在上图中,∠1与∠3有什么数量关系?
互为补角:如果两个角的和是180°,
那么称这两个角互为补角.
互为余角:如果两个角的和是90°,
那么称这两个角互为余角.
已知∠1=50°,它的余角是多少度?
它的补角是多少度?
已知∠3=150°,它的补角是多少度?
互为补角的两个角可以都是锐角吗?可以都是直角吗?可以都是钝角吗?
思考:
如图所示,已知:直线AB与CD交于点O, ∠EOD=900 :哪些角互为余角?哪些角互为补角?
C
A
B
D
O
E
(1)哪些角互为补角?哪些角互为余角?
将实物图抽象简化成几何图形,
ON与DC交于点O,∠DON=∠CON=900,∠1=∠2
(2)∠3和∠4有什么关系?为什么?
(3)∠AOC和∠BOD有什么关系?为什么?
同角或等角的余角相等
∵∠1=∠2
∠1+∠3=90
∠2+∠4=90
∴ ∠3= ∠4
(等 角的余角相等)
图形语言:
文字语言:
几何语言:
同角或等角的补角相等
∵∠1=∠2 ∠1+∠AOC=180 ∠2+∠DOB=180
∴ ∠AOC= ∠DOB
(等角的补角相等)
图形语言:
文字语言:
几何语言:
1.①.因为∠1+∠2=90 ,∠2+∠3=90 ,所以∠1= ,理由是 .
② 因为∠1+∠2=180 ,∠2+∠3=180 ,所以∠1= ,理由是 .
你有哪些收获?知道了哪些概念?学会了什么方法?
小结
A
B
C
D
F
G
O
E
拓展:
一个角的补角加上10°后等于这个角的余角的3倍,求这个角的度数。
2.如图,点O在直线AB上,∠DOC和∠BOE都等于900.
A
O
B
D
C
E
请找出图中互余的角、互补的角、相等的角,并说明理由。
2.1.1两条直线间的关系
公园一角,
亭台楼阁
整齐的自行车棚
漂亮的小木栅栏
想一想:上述图片中的两条直线有哪几种位置关系?
若两条直线只有一个公共点,我们称这两条直线为相交线。
在同一平面内,不相交的两条直线叫做平行线。
请动手画出两条直线AB和CD,
交于点O.
活动1 观察你所画图形。
∠1和∠2的位置有什么关系?
我们先来研究两条直线相交的情况:
1
2
1
2
1
2
1
2
A
B
C
D
1、下列各图中,∠1和∠2是对顶角的是( )
2.下列各图中,∠1与∠2互为对顶角的是( )
3.如图,在所标识的角中,互为对顶角的两个角是( )
(A)∠2和∠3 (B)∠1和∠3
(C)∠1和∠4 (D)∠1和∠2
找出对顶角
A
B
C
D
E
F
O
活动2:任意一组对顶角大小有何关系?
∵直线AB与CD相交于点O
对顶角相等
3
2
1
4
A
B
C
D
o
∴ ∠1=∠2, ∠3=∠4 (对顶角相等)
文字语言:
几何语言:
联系生活
有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
3
2
1
4
A
B
C
D
o
3
2
1
4
A
B
C
D
o
在上图中,∠1与∠3有什么数量关系?
互为补角:如果两个角的和是180°,
那么称这两个角互为补角.
互为余角:如果两个角的和是90°,
那么称这两个角互为余角.
已知∠1=50°,它的余角是多少度?
它的补角是多少度?
已知∠3=150°,它的补角是多少度?
互为补角的两个角可以都是锐角吗?可以都是直角吗?可以都是钝角吗?
思考:
如图所示,已知:直线AB与CD交于点O, ∠EOD=900 :哪些角互为余角?哪些角互为补角?
C
A
B
D
O
E
(1)哪些角互为补角?哪些角互为余角?
将实物图抽象简化成几何图形,
ON与DC交于点O,∠DON=∠CON=900,∠1=∠2
(2)∠3和∠4有什么关系?为什么?
(3)∠AOC和∠BOD有什么关系?为什么?
同角或等角的余角相等
∵∠1=∠2
∠1+∠3=90
∠2+∠4=90
∴ ∠3= ∠4
(等 角的余角相等)
图形语言:
文字语言:
几何语言:
同角或等角的补角相等
∵∠1=∠2 ∠1+∠AOC=180 ∠2+∠DOB=180
∴ ∠AOC= ∠DOB
(等角的补角相等)
图形语言:
文字语言:
几何语言:
1.①.因为∠1+∠2=90 ,∠2+∠3=90 ,所以∠1= ,理由是 .
② 因为∠1+∠2=180 ,∠2+∠3=180 ,所以∠1= ,理由是 .
你有哪些收获?知道了哪些概念?学会了什么方法?
小结
A
B
C
D
F
G
O
E
拓展:
一个角的补角加上10°后等于这个角的余角的3倍,求这个角的度数。
2.如图,点O在直线AB上,∠DOC和∠BOE都等于900.
A
O
B
D
C
E
请找出图中互余的角、互补的角、相等的角,并说明理由。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
