9.4 解直角三形

解直角三角形
班级 姓名 编写：宋丽丽 审核： 初二数学组
学习目标：
了解解直角三角形的定义；
综合运用勾股定理，直角三角形的两角关系，锐角三角比解直角三角形。
2、通过小组合作交流，了解数形结合的思想，培养学生自主探究的能力。
3、培养学生的爱国主义精神，并在学习活动中获得成功的体验。
学习重点与难点：
重点：解直角三角形；
难点：将实际问题抽象为数学问题，探索解决问题的有效方法。
课前案
一、温故知新：
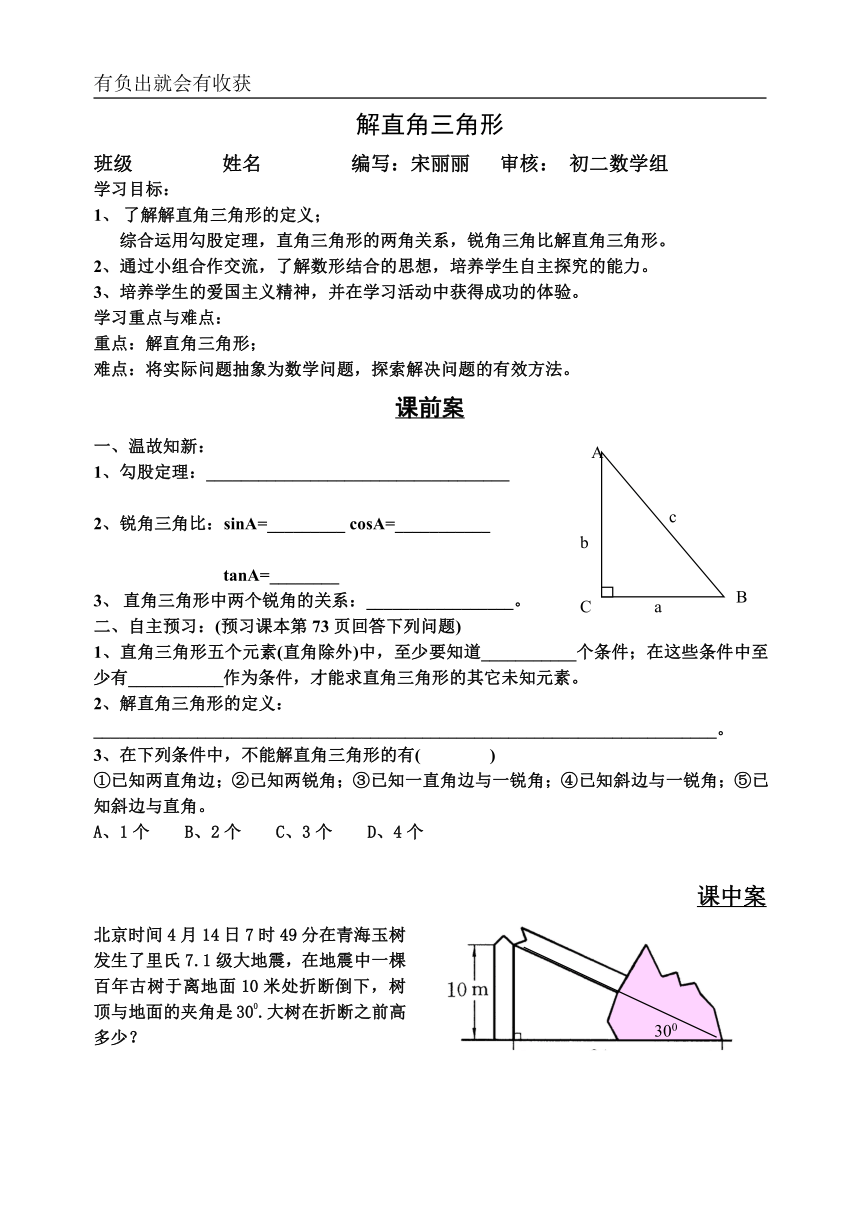
1、勾股定理：___________________________________
2、锐角三角比：sinA=_________ cosA=___________
tanA=________
直角三角形中两个锐角的关系：_________________。
二、自主预习：(预习课本第73页回答下列问题)
1、直角三角形五个元素(直角除外)中，至少要知道___________个条件；在这些条件中至少有___________作为条件，才能求直角三角形的其它未知元素。
2、解直角三角形的定义：
________________________________________________________________________。
3、在下列条件中，不能解直角三角形的有( )
①已知两直角边；②已知两锐角；③已知一直角边与一锐角；④已知斜边与一锐角；⑤已知斜边与直角。
A、1个 B、2个 C、3个 D、4个
课中案
北京时间4月14日7时49分在青海玉树发生了里氏7.1级大地震，在地震中一棵百年古树于离地面10米处折断倒下，树顶与地面的夹角是300.大树在折断之前高多少？
课内探究
自主学习：看书P74例1与例2，完成对例题的学习，
归纳小结：1、已知两边(1)求第三边：___________________________；
(2)求锐角________________________________
2、已知一边与一锐角：(1)求角：______________________
(2)求边：_______________________________。
（二）合作交流：将引入问题及自主学习中不明白问题进行交流。
（三）精讲点拨：
1、解决情景引入的问题：
变式：如果折断后树顶到树根部的距离为10米，那大树的原来的高度。
（四）巩固检测----有效训练
1、已知Rt△ABC中，∠C=900，a=1，b=，请按以下过程解此直角三角形：
①最容易求的元素是c边，可以用勾股定理来求：________________________；
②要求∠A，可选锐角三角比中的正切，利用特殊角的三角比来求：
即：∵ ____________________ ∴_____________________
③最后求∠B，利用直角三角形两锐角互余的关系求得：_______________________
2、 已知Rt△ABC中，∠C=900，b=6，∠A=300，请按以下过程解此直角三角形：
①最容易求的元素是∠B，可以利用直角三角形两锐角互余的关系求得：________________________；
②要求c边，可选锐角三角比中的余弦，利用特殊角的三角比来求：
即：∵ ____________________ ∴ _____________________
③最后求c边，可利用勾股定理求得：_______________________(想一想：还可以利用什么求得c边？)
3、已知Rt△ABC中，∠C=900，a=4，c=8，解此直角三角形.
课堂小结：
1、本节课你有哪些收获？
2、应该注意的问题有哪些？
巩固检测----当堂检测：
（1）在Rt△ABC中，∠C为直角，根据下列条件不能解的直角三角形是( )
A、∠A=450，AB=5 B、AC=3 BC=4 C、∠A=300，∠B=600 D、∠A=300，AB=9
2、在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别是a、b、c，已知∠A=300，c=10，则b的值是( )
A、 B、 C、5 D、8
3、在Rt△ABC中，∠C=90°，已知边α和∠A 求c边，则选用下列关系式正确的是( )
（A）（B）（C）（D）
4、在△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边。已知∠A=30°，b=2，

则∠B=_________，边a=______________，边c=_______________。
课后提升
必做题：课本第74练习。
选作题：课本第75习题9.4A组1、2题。
1．在△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边。
（1）已知∠A=30°，b=2，求cosB和a。
（2）已知c=5，a=1，求tanB和b。
（3）已知tanA=，b=2，求c和sinB。

2．已知：在直角梯形ABCD中，AB∥CD，∠D=90°，AC⊥BC，且AD=4，DC=3，求AB的长。
3．已知：△ABC中，AD⊥BC于D，∠B=45°，DC=1，S△ABC=6，求AC的长。