6.1.1.1数的认识(一)导学案2 六年级数学下册-人教版
文档属性
| 名称 | 6.1.1.1数的认识(一)导学案2 六年级数学下册-人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 102.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 09:54:40 | ||
图片预览


文档简介
6.1.1.1 数的认识(一)
导学案
学习目标
1、进一步体会整数、自然数、分数、小数、正数、负数、百分数的意义及其彼此之间的联系,形成知识网络。
2、进一步深化对十进制计数法、计数单位的认识。初步尝试列提纲以及用框架图来整理复习内容。
重点:
进一步体会各种数的意义及其彼此之间的联系。
难点:
沟通各类数之间的联系,形成知识网络。
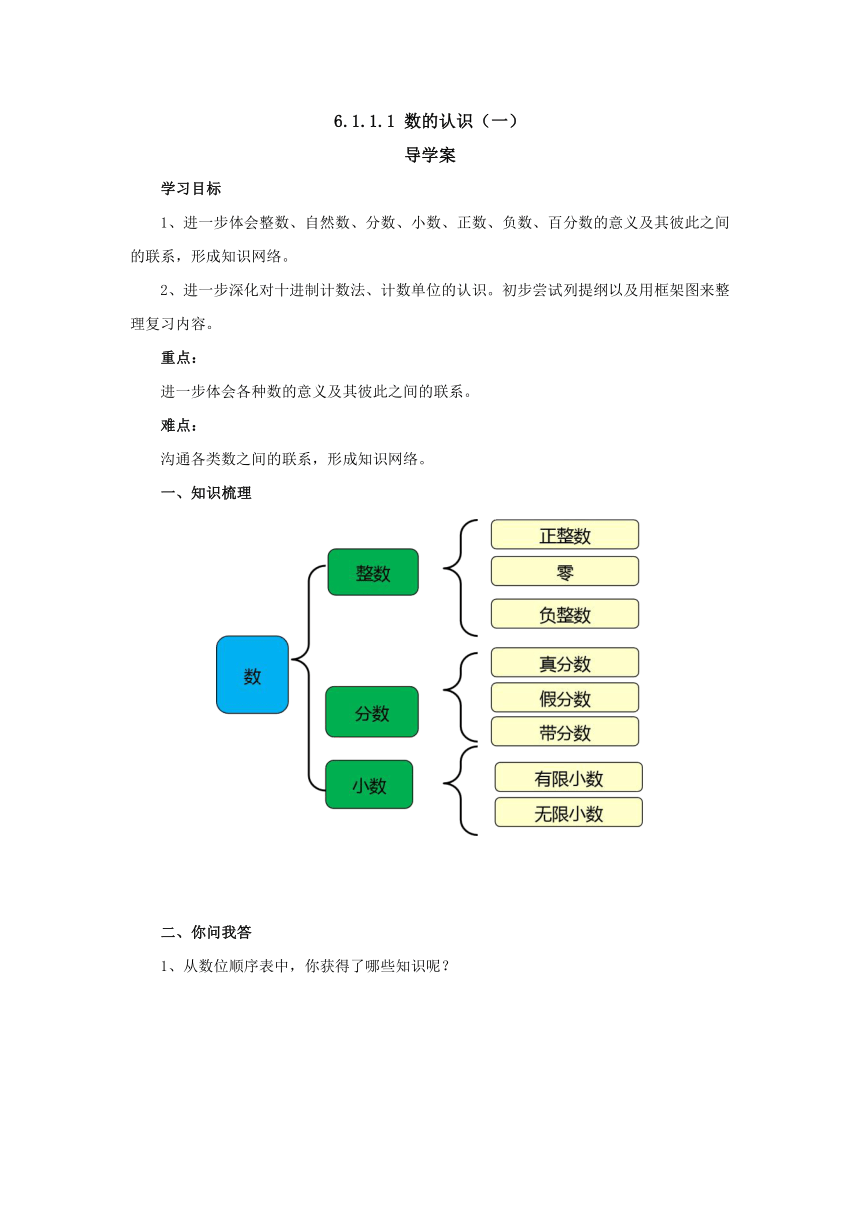
一、知识梳理
二、你问我答
1、从数位顺序表中,你获得了哪些知识呢?
数位、计数单位、整数部分、小数点、小数部分
2、整数与小数有哪些联系与区别?
整数和小数都是按十进制计数法写出的数,其中个、十、 百……以及十分之一、百分之一……都是计数单位。各个 计数单位所占的位置,叫做数位。数位是按一定顺序排列的。整数的最小计数单位是1,而小数没有最小的计数单位。
3、关于小数你能想到哪些知识?可以举例说明。
小数的基本性质,如5.06和5.0600大小相等。
小数点位置移动引起大小变化。比如0.5和0.05大小不等。
4、为什么5.06和5.0600大小相等呢?
不管在小数的末尾添上几个0,或去掉几个0,5和6所在数位没变,计数单位也就没有变,所以大小相等。
5、分数单位与整数、小数的计数单位有什么不同?
把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。像一(个)、十、百、千、万、十万……以及十分之一,百分之一……等,是整数、小数的计数单位。每相邻两个计数单位之间的进率是“十”。
6、百分数是分数中的一种特殊形式。二者的联系是什么?
联系:都能表示一个数与另一个数之间的比率,
百分数所表示的含义是一个数是另一个数的百分之几,
是分数的一种特殊表示形式。分数和百分数可以互相转化。
二者的区别是什么?
百分数和分数的写法不同;
分数既可以表示率,也可以表示量,但百分数只可以表示率;
分数可以约成最简分数,可是百分数不能进行约分;
分数的分子只能是整数,而百分数的子既可以是整数,也可以是小数。
三、填一填。
1、10个一万是( )。 ( )个十万是一百万。 10( )是一千万。
2、按照我国的计数习惯,从右边起,每( )个数位是一级。个位、十位、百位、千位是( ),( )是万级。
3、读数时,要从( )起一级一级往下读,万级或亿级的数要按照( )的读法来读,再在后面读出“( )”或“( )”字。写数时,也要从( )到( )一级一级的写。
4、读数时,每级末尾的0都( ),其他数位有一个0或连续几个0,都( )。
5、比较多位数的大小,先看数位,( )的数大,数位相同时,先比较( ),( )位上大的数就大,最高位相同,再比较( )。 直到( )为止。
6、把整万或整亿改写成用“万”或“亿”作单位的数时,去掉( )位的后面的零,再在数的后面带上( )。
7、像+13、+831.7 都是( )数,“+”是正号,通常省略不写。像-3、-155.31 都是( )数,“-”是负号。
8、0既不是( ),也不是( )。
9、具有( )意义的量,可以用正、负数表示。
10、把( )平均分成若干份,表示这样的( )的数,叫做分数。表示这样( )份的数叫做分数单位。
11、被除数相当于分数的( ),除数相当于分数的( )。
12、表示十分之几、百分之几、千分之几······ 的数叫作( )。
13、小数包括( )和( )。
四、题型、技巧归纳与典例精讲
1、这些都是什么数?说一说每个数的具体含义。
(1)某地的海拔高度844.43m。
(2)一件羽绒服的成分:羽绒95%、羽毛5%。
(3)某段时间内,某市空气1级天数约占总天数的 。
(4)北极洲年平均气温只有-25℃。
(5)青岛市在2018年植树20多万棵。
方法指导:把小数点对齐,从末位加起,哪一位上的数相加满十,就向前一位进1,最后在得数里对齐横线上的小数点,点上小数点。
2、数的改写。
(1)把2500改写成用“万”作单位的数是( )。
(2)8.495保留一位小数是( ),保留两位小数是( )。
方法指导:把整万或整亿改写成用“万”或“亿”作单位的数时,去掉万位或亿位位的后面的零,再在数的后面带上“万”或“亿”。
小数的保留到哪一位,看它的下一位,用“四舍五入”的方法保留。
3、分数与除法的关系。
(1)。
(2)把一根3米长的绳子剪成同样长的8段,每段长是全长的 ,每段长米
方法指导:被除数相当分数的分子,除数相当于分数的分母。
五、课堂小结
说说你的收获吧!
整数和小数都是按十进制计数法写出的数,其中个、十、 百……以及十分之一、百分之一……都是计数单位。
各个计数单位所占的位置,叫做数位。数位是按一定顺序排列的。整数的最小计数单位是1,而小数没有最小的计数单位。
把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。像一(个)、十、百、千、万、十万……以及十分之一,百分之一……等,是整数、小数的计数单位。每相邻两个计数单位之间的进率是“十”。
导学案
学习目标
1、进一步体会整数、自然数、分数、小数、正数、负数、百分数的意义及其彼此之间的联系,形成知识网络。
2、进一步深化对十进制计数法、计数单位的认识。初步尝试列提纲以及用框架图来整理复习内容。
重点:
进一步体会各种数的意义及其彼此之间的联系。
难点:
沟通各类数之间的联系,形成知识网络。
一、知识梳理
二、你问我答
1、从数位顺序表中,你获得了哪些知识呢?
数位、计数单位、整数部分、小数点、小数部分
2、整数与小数有哪些联系与区别?
整数和小数都是按十进制计数法写出的数,其中个、十、 百……以及十分之一、百分之一……都是计数单位。各个 计数单位所占的位置,叫做数位。数位是按一定顺序排列的。整数的最小计数单位是1,而小数没有最小的计数单位。
3、关于小数你能想到哪些知识?可以举例说明。
小数的基本性质,如5.06和5.0600大小相等。
小数点位置移动引起大小变化。比如0.5和0.05大小不等。
4、为什么5.06和5.0600大小相等呢?
不管在小数的末尾添上几个0,或去掉几个0,5和6所在数位没变,计数单位也就没有变,所以大小相等。
5、分数单位与整数、小数的计数单位有什么不同?
把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。像一(个)、十、百、千、万、十万……以及十分之一,百分之一……等,是整数、小数的计数单位。每相邻两个计数单位之间的进率是“十”。
6、百分数是分数中的一种特殊形式。二者的联系是什么?
联系:都能表示一个数与另一个数之间的比率,
百分数所表示的含义是一个数是另一个数的百分之几,
是分数的一种特殊表示形式。分数和百分数可以互相转化。
二者的区别是什么?
百分数和分数的写法不同;
分数既可以表示率,也可以表示量,但百分数只可以表示率;
分数可以约成最简分数,可是百分数不能进行约分;
分数的分子只能是整数,而百分数的子既可以是整数,也可以是小数。
三、填一填。
1、10个一万是( )。 ( )个十万是一百万。 10( )是一千万。
2、按照我国的计数习惯,从右边起,每( )个数位是一级。个位、十位、百位、千位是( ),( )是万级。
3、读数时,要从( )起一级一级往下读,万级或亿级的数要按照( )的读法来读,再在后面读出“( )”或“( )”字。写数时,也要从( )到( )一级一级的写。
4、读数时,每级末尾的0都( ),其他数位有一个0或连续几个0,都( )。
5、比较多位数的大小,先看数位,( )的数大,数位相同时,先比较( ),( )位上大的数就大,最高位相同,再比较( )。 直到( )为止。
6、把整万或整亿改写成用“万”或“亿”作单位的数时,去掉( )位的后面的零,再在数的后面带上( )。
7、像+13、+831.7 都是( )数,“+”是正号,通常省略不写。像-3、-155.31 都是( )数,“-”是负号。
8、0既不是( ),也不是( )。
9、具有( )意义的量,可以用正、负数表示。
10、把( )平均分成若干份,表示这样的( )的数,叫做分数。表示这样( )份的数叫做分数单位。
11、被除数相当于分数的( ),除数相当于分数的( )。
12、表示十分之几、百分之几、千分之几······ 的数叫作( )。
13、小数包括( )和( )。
四、题型、技巧归纳与典例精讲
1、这些都是什么数?说一说每个数的具体含义。
(1)某地的海拔高度844.43m。
(2)一件羽绒服的成分:羽绒95%、羽毛5%。
(3)某段时间内,某市空气1级天数约占总天数的 。
(4)北极洲年平均气温只有-25℃。
(5)青岛市在2018年植树20多万棵。
方法指导:把小数点对齐,从末位加起,哪一位上的数相加满十,就向前一位进1,最后在得数里对齐横线上的小数点,点上小数点。
2、数的改写。
(1)把2500改写成用“万”作单位的数是( )。
(2)8.495保留一位小数是( ),保留两位小数是( )。
方法指导:把整万或整亿改写成用“万”或“亿”作单位的数时,去掉万位或亿位位的后面的零,再在数的后面带上“万”或“亿”。
小数的保留到哪一位,看它的下一位,用“四舍五入”的方法保留。
3、分数与除法的关系。
(1)。
(2)把一根3米长的绳子剪成同样长的8段,每段长是全长的 ,每段长米
方法指导:被除数相当分数的分子,除数相当于分数的分母。
五、课堂小结
说说你的收获吧!
整数和小数都是按十进制计数法写出的数,其中个、十、 百……以及十分之一、百分之一……都是计数单位。
各个计数单位所占的位置,叫做数位。数位是按一定顺序排列的。整数的最小计数单位是1,而小数没有最小的计数单位。
把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。像一(个)、十、百、千、万、十万……以及十分之一,百分之一……等,是整数、小数的计数单位。每相邻两个计数单位之间的进率是“十”。
