人教版 六年级数学下册 6.2.1平面图形的认识 导学案
文档属性
| 名称 | 人教版 六年级数学下册 6.2.1平面图形的认识 导学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 200.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 10:43:50 | ||
图片预览


文档简介
6.2.1 平面图形的认识
复习目标
1、在整理和复习中,经历对平面图形有关知识系统复习与整理的过程。
2、进一步理解并掌握平面图形有关知识,能用平面图形有关知识解决实际问题。
重点:
进一步理解并掌握平面图形有关知识,能用平面图形有关知识解决实际问题。
难点:
进一步理解并掌握平面图形有关知识,能用平面图形有关知识解决实际问题。
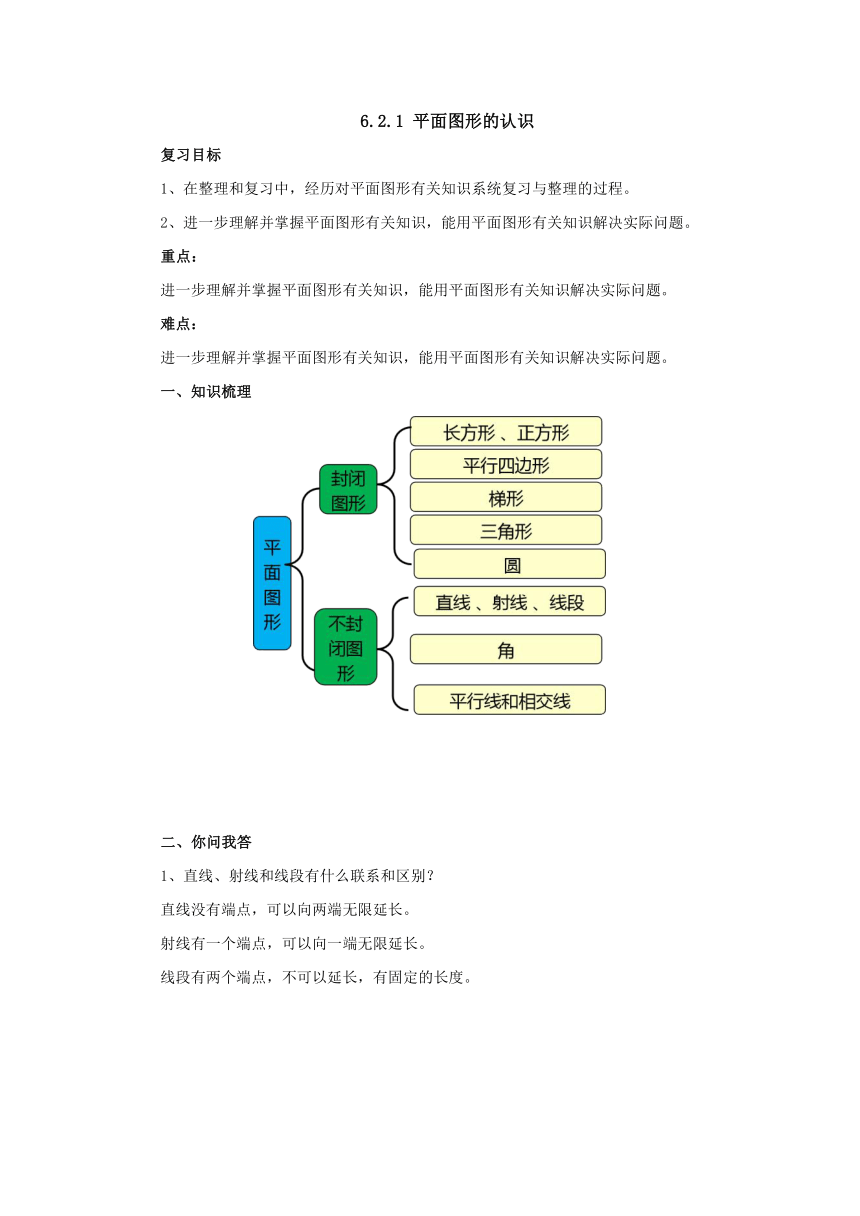
一、知识梳理
二、你问我答
1、直线、射线和线段有什么联系和区别?
直线没有端点,可以向两端无限延长。
射线有一个端点,可以向一端无限延长。
线段有两个端点,不可以延长,有固定的长度。
2、同一平面内的两条直线有哪几种位置关系?
相交和平行
3、你学过哪些四边形,能说说它们之间的关系吗?
三、填一填。
1、把线段的一端( ),就得到一条射线。
2、把线段的( )无限延长,就得到一条直线。
3、射线、直线和线段相比( );( )。
4、连接两点的线段的长度叫作( )。
5、从一点引出的两条射线可以组成( )。角通常用符合“( )”表示。
6、先把量角器的中心点与( )重合,0°刻度线和( )重合,再看看( )所对的刻度是多少,这个角就是( )。
7、垂线的画法:把三角板的一条直角边和( )重合; 使三角板的( )过点A。用笔顺着三角板的另一条直角画出已知直线的( )。
8、平行线的画法:画平行线时可以在( )上画;也可以沿着( )的对边画。
9、三角形由( )条边围成的图形,每一个三角形都有( )个角,( )顶点。
10、三角形任意两边长度的和( )第三边。
11、三角形的内角和等于( )。
12、三角形按角分可以分成( )、( )、( )。
13、等腰三角形的底角( )。等腰三角形是( )图形。等腰三角形底边上的高在它的( )上。
14、等边三角形的3个角( )。等边三角形是( )图形。等边三角形有( )条对称轴。
15、两组对边分别平行的四边形叫作( )。
16、从平行四边形一条边上的一点到它的对边的( )线段,是平行四边形的高,这条对边是平行四边形的( )。
17、( )的四边形叫作梯形。互相平行的一组对边是梯形的( )和( ),不平行的一组对边是梯形的( )。
18、从梯形一条底边上的一点到它对边的垂直线段叫作梯形的( )。
19、两腰相等的梯形是( )。
20、 ( )叫做圆的半径。一般用字母( )表示。
四、题型、技巧归纳与典例精讲
1、下图中有几条射线?组成了几个角?你能指出每个角的顶点和边吗?
方法指导:从一点引出的两条射线可以组成角。
3条射线 3个角。
2、用量角器量出下面各角的度数。
方法指导:先把量角器的中心点与角的顶点重合,0°刻度线和角的一条边重合,再看看另一条边所对的刻度是多少,这个角就是多少度的角。
3、你能把下边的图形补充成长方形吗?
方法提示:既可以用垂线的画法也可以用平行线的画法来画。
4、下面各是什么图形?它们有什么不同?分别画出每个图形底边上的高。
方法提示:利用三角板的两条直角边画出高。
5、在三角形中,已知∠1=42°,∠2=68°,求∠3的度数。
方法提示:三角形的内角和是180°。
180°-42°-68°
=138°-68°
=70°
答:∠3的度数是70°。
五、课堂小结
说说你的收获吧!
直线没有端点,射线有一个端点,线段有两个端点,不可以延长,有固定的长度。
三条线段首尾相接围成的图形叫作三角形。
两组对边分别平行的四边形叫作平行四边形。只有一组对边平行的四边形叫作梯形。
圆的半径和直径都可以画无数条。同一个圆里,所有的半径都相等,所以的直径都相等。
复习目标
1、在整理和复习中,经历对平面图形有关知识系统复习与整理的过程。
2、进一步理解并掌握平面图形有关知识,能用平面图形有关知识解决实际问题。
重点:
进一步理解并掌握平面图形有关知识,能用平面图形有关知识解决实际问题。
难点:
进一步理解并掌握平面图形有关知识,能用平面图形有关知识解决实际问题。
一、知识梳理
二、你问我答
1、直线、射线和线段有什么联系和区别?
直线没有端点,可以向两端无限延长。
射线有一个端点,可以向一端无限延长。
线段有两个端点,不可以延长,有固定的长度。
2、同一平面内的两条直线有哪几种位置关系?
相交和平行
3、你学过哪些四边形,能说说它们之间的关系吗?
三、填一填。
1、把线段的一端( ),就得到一条射线。
2、把线段的( )无限延长,就得到一条直线。
3、射线、直线和线段相比( );( )。
4、连接两点的线段的长度叫作( )。
5、从一点引出的两条射线可以组成( )。角通常用符合“( )”表示。
6、先把量角器的中心点与( )重合,0°刻度线和( )重合,再看看( )所对的刻度是多少,这个角就是( )。
7、垂线的画法:把三角板的一条直角边和( )重合; 使三角板的( )过点A。用笔顺着三角板的另一条直角画出已知直线的( )。
8、平行线的画法:画平行线时可以在( )上画;也可以沿着( )的对边画。
9、三角形由( )条边围成的图形,每一个三角形都有( )个角,( )顶点。
10、三角形任意两边长度的和( )第三边。
11、三角形的内角和等于( )。
12、三角形按角分可以分成( )、( )、( )。
13、等腰三角形的底角( )。等腰三角形是( )图形。等腰三角形底边上的高在它的( )上。
14、等边三角形的3个角( )。等边三角形是( )图形。等边三角形有( )条对称轴。
15、两组对边分别平行的四边形叫作( )。
16、从平行四边形一条边上的一点到它的对边的( )线段,是平行四边形的高,这条对边是平行四边形的( )。
17、( )的四边形叫作梯形。互相平行的一组对边是梯形的( )和( ),不平行的一组对边是梯形的( )。
18、从梯形一条底边上的一点到它对边的垂直线段叫作梯形的( )。
19、两腰相等的梯形是( )。
20、 ( )叫做圆的半径。一般用字母( )表示。
四、题型、技巧归纳与典例精讲
1、下图中有几条射线?组成了几个角?你能指出每个角的顶点和边吗?
方法指导:从一点引出的两条射线可以组成角。
3条射线 3个角。
2、用量角器量出下面各角的度数。
方法指导:先把量角器的中心点与角的顶点重合,0°刻度线和角的一条边重合,再看看另一条边所对的刻度是多少,这个角就是多少度的角。
3、你能把下边的图形补充成长方形吗?
方法提示:既可以用垂线的画法也可以用平行线的画法来画。
4、下面各是什么图形?它们有什么不同?分别画出每个图形底边上的高。
方法提示:利用三角板的两条直角边画出高。
5、在三角形中,已知∠1=42°,∠2=68°,求∠3的度数。
方法提示:三角形的内角和是180°。
180°-42°-68°
=138°-68°
=70°
答:∠3的度数是70°。
五、课堂小结
说说你的收获吧!
直线没有端点,射线有一个端点,线段有两个端点,不可以延长,有固定的长度。
三条线段首尾相接围成的图形叫作三角形。
两组对边分别平行的四边形叫作平行四边形。只有一组对边平行的四边形叫作梯形。
圆的半径和直径都可以画无数条。同一个圆里,所有的半径都相等,所以的直径都相等。
