人教版 六年级数学下册 6.2.3立体图形 导学案
文档属性
| 名称 | 人教版 六年级数学下册 6.2.3立体图形 导学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 149.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 10:55:19 | ||
图片预览


文档简介
6.2.3 立体图形
复习目标
1、在整理和复习中,经历对立体图形有关知识系统复习与整理的过程。
2、进一步理解并掌握立体图形有关知识,能用立体图形有关知识解决实际问题。
3、培养回顾与复习的好习惯,查漏补缺,获得积极的学习体验。
重点:
进一步理解并掌握立体图形有关知识,能用立体图形有关知识解决实际问题。
难点:
进一步理解并掌握立体图形有关知识,能用立体图形有关知识解决实际问题。
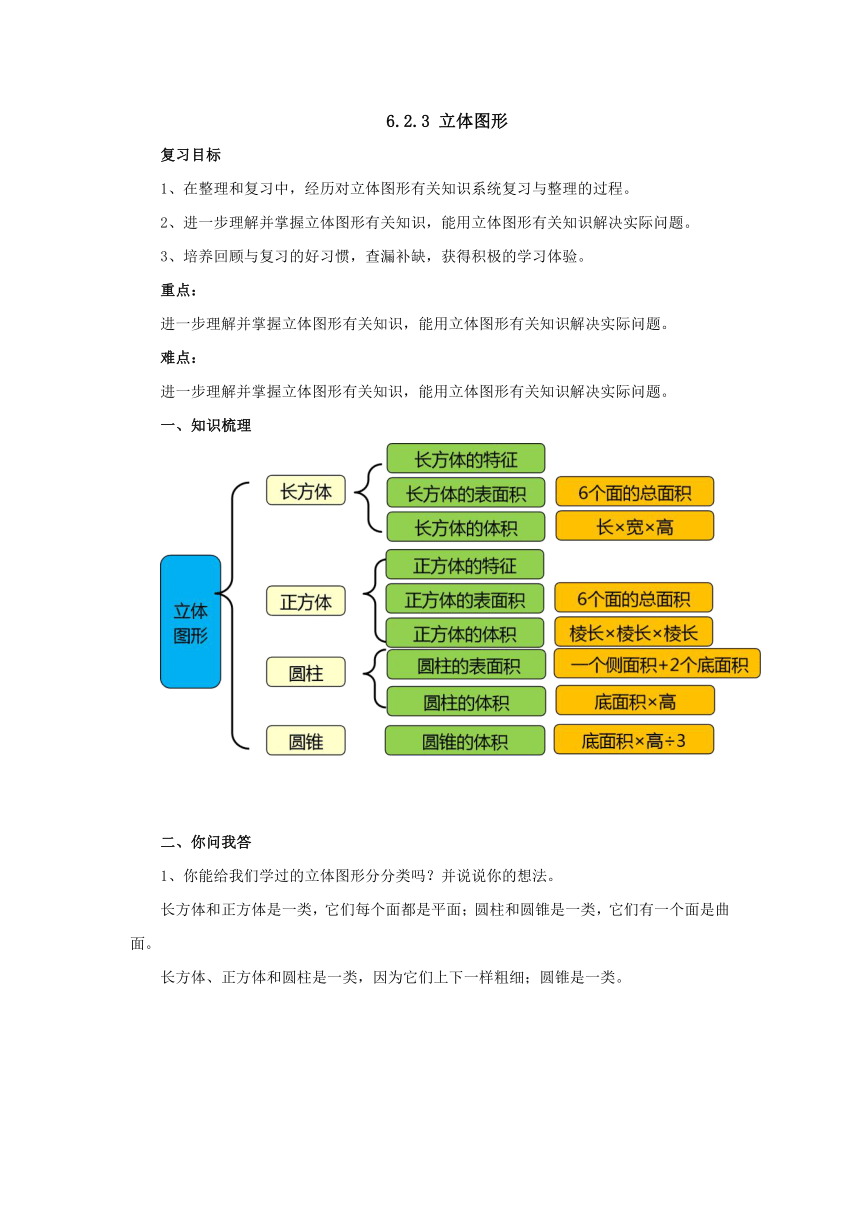
一、知识梳理
二、你问我答
1、你能给我们学过的立体图形分分类吗?并说说你的想法。
长方体和正方体是一类,它们每个面都是平面;圆柱和圆锥是一类,它们有一个面是曲面。
长方体、正方体和圆柱是一类,因为它们上下一样粗细;圆锥是一类。
2、你能说说长方体和正方体的关系吗?
正方体是特殊的长方体。
3、我们学过的立体图形的体积公式是怎么推导出来的呀?它们之间有联系吗?
正方体和圆柱的体积公式都是在长方体体积公式的基础上推导出来的。
三、填一填
1、两个面相交的线叫作( ),三条棱相交的点叫作( )。
2、相交于一个顶点的三条棱的长度,分别叫作长方体的( )、( )、( )。正方体的12条棱都( )。
3、长方体和正方体都有( )个顶点,( )个面,( )条棱,正方体的6个面,是完全相同的( )。正方体是( )的长方体。
4、圆柱的上、下两个面叫作圆柱的( ),围成圆柱的曲面叫作圆柱的( )。
5、圆柱两个( )之间的距离叫作圆柱的高。
6、圆锥有一个( ),底面是一个( ),侧面是一个( )。
7、从圆锥的( )到( )的距离叫作圆锥的高。
8、正方体的表面积=( )。
9、长方体的体积 =( ), 用字母表示( ) 。
10、正方体的体积 = ( ) ,用字母表示( ) 。
11、长方体(或正方体)的体积=( ), 用字母表示 ( ) 。
12、长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器( )量长。
13、在探究圆柱的体积时,圆柱体平均分的份数越多,拼成的物体就越接近( )。
14、在探究圆柱的体积时,拼成的长方体的与原来的圆柱相比,长方体的体积与( )相等,长方体的底面积等于( )。长方体的高等于( )。
15、圆柱的体积=( ),用字母表示( )。
16、圆锥的体积=( ),用字母表示为( )。
四、题型、技巧归纳与典例精讲
1、用铁丝焊接一个长6厘米、宽5厘米、高4厘米的长方形框架,至少需要铁丝多少厘米?如果要焊接一个棱长5厘米的正方形框架呢?
方法指导:长方体的棱长之和=(长+宽+高)×4;正方体的棱长之和=棱长×12。
(6+5+4)×4
=15×4
=60(厘米)
答:至少需要铁丝60厘米。
5×12=60(厘米)
答:至少需要铁丝60厘米。
2、一个长5分米、宽3分米、高1.5分米的抽屉(如图),需要多少平方分米的木板?(木板的厚度忽略不计)
方法指导:求抽屉的表面积不包括上面,求其余五个面的面积。
5×3+(5×1.5+3×1.5)×2
=15+(7.5+4.5)×2
=15+12×2
=39(平方分米)
答:需要39平方分米的木板。
3、一个近似于圆锥形的稻谷堆,底面直径是4米,高是1.5米。如果每立方米稻谷大约重0.55吨,这堆稻谷大约重多少吨?(得数保留整数)
方法指导:圆锥的体积积=×底面积×高
×3.14×(4÷2)2×1.5×0.55
=3.14×4×0.5×0.55
=3.454
≈3(吨)
五、课堂小结
说说你的收获吧!
长方体和正方体都有8个顶点,6个面,12条棱,正方体有6个面,它们是完全相同的正方形。正方体是特殊的长方体。
长(正)方体的表面积就是求它的6个面的总面积。圆柱的表面积=2个底面积+侧面积。
长方体(或正方体)的体积=底面积×高 V =Sh。
圆柱的体积: V =Sh。
圆锥的体积:V = Sh。
复习目标
1、在整理和复习中,经历对立体图形有关知识系统复习与整理的过程。
2、进一步理解并掌握立体图形有关知识,能用立体图形有关知识解决实际问题。
3、培养回顾与复习的好习惯,查漏补缺,获得积极的学习体验。
重点:
进一步理解并掌握立体图形有关知识,能用立体图形有关知识解决实际问题。
难点:
进一步理解并掌握立体图形有关知识,能用立体图形有关知识解决实际问题。
一、知识梳理
二、你问我答
1、你能给我们学过的立体图形分分类吗?并说说你的想法。
长方体和正方体是一类,它们每个面都是平面;圆柱和圆锥是一类,它们有一个面是曲面。
长方体、正方体和圆柱是一类,因为它们上下一样粗细;圆锥是一类。
2、你能说说长方体和正方体的关系吗?
正方体是特殊的长方体。
3、我们学过的立体图形的体积公式是怎么推导出来的呀?它们之间有联系吗?
正方体和圆柱的体积公式都是在长方体体积公式的基础上推导出来的。
三、填一填
1、两个面相交的线叫作( ),三条棱相交的点叫作( )。
2、相交于一个顶点的三条棱的长度,分别叫作长方体的( )、( )、( )。正方体的12条棱都( )。
3、长方体和正方体都有( )个顶点,( )个面,( )条棱,正方体的6个面,是完全相同的( )。正方体是( )的长方体。
4、圆柱的上、下两个面叫作圆柱的( ),围成圆柱的曲面叫作圆柱的( )。
5、圆柱两个( )之间的距离叫作圆柱的高。
6、圆锥有一个( ),底面是一个( ),侧面是一个( )。
7、从圆锥的( )到( )的距离叫作圆锥的高。
8、正方体的表面积=( )。
9、长方体的体积 =( ), 用字母表示( ) 。
10、正方体的体积 = ( ) ,用字母表示( ) 。
11、长方体(或正方体)的体积=( ), 用字母表示 ( ) 。
12、长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器( )量长。
13、在探究圆柱的体积时,圆柱体平均分的份数越多,拼成的物体就越接近( )。
14、在探究圆柱的体积时,拼成的长方体的与原来的圆柱相比,长方体的体积与( )相等,长方体的底面积等于( )。长方体的高等于( )。
15、圆柱的体积=( ),用字母表示( )。
16、圆锥的体积=( ),用字母表示为( )。
四、题型、技巧归纳与典例精讲
1、用铁丝焊接一个长6厘米、宽5厘米、高4厘米的长方形框架,至少需要铁丝多少厘米?如果要焊接一个棱长5厘米的正方形框架呢?
方法指导:长方体的棱长之和=(长+宽+高)×4;正方体的棱长之和=棱长×12。
(6+5+4)×4
=15×4
=60(厘米)
答:至少需要铁丝60厘米。
5×12=60(厘米)
答:至少需要铁丝60厘米。
2、一个长5分米、宽3分米、高1.5分米的抽屉(如图),需要多少平方分米的木板?(木板的厚度忽略不计)
方法指导:求抽屉的表面积不包括上面,求其余五个面的面积。
5×3+(5×1.5+3×1.5)×2
=15+(7.5+4.5)×2
=15+12×2
=39(平方分米)
答:需要39平方分米的木板。
3、一个近似于圆锥形的稻谷堆,底面直径是4米,高是1.5米。如果每立方米稻谷大约重0.55吨,这堆稻谷大约重多少吨?(得数保留整数)
方法指导:圆锥的体积积=×底面积×高
×3.14×(4÷2)2×1.5×0.55
=3.14×4×0.5×0.55
=3.454
≈3(吨)
五、课堂小结
说说你的收获吧!
长方体和正方体都有8个顶点,6个面,12条棱,正方体有6个面,它们是完全相同的正方形。正方体是特殊的长方体。
长(正)方体的表面积就是求它的6个面的总面积。圆柱的表面积=2个底面积+侧面积。
长方体(或正方体)的体积=底面积×高 V =Sh。
圆柱的体积: V =Sh。
圆锥的体积:V = Sh。
