2021-2022学年鲁教版(五四制)七年级数学下册第7章二元一次方程组单元综合练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学下册第7章二元一次方程组单元综合练习题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览




文档简介
2021-2022学年鲁教版七年级数学下册《第7章二元一次方程组》单元综合练习题(附答案)
1.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;④若2x+y=8,则a=2.正确的有几个( )
A.1 B.2 C.3 D.4
2.太原市城乡居民用电价格按用电需求分为三个档次,电价分档递增:第一档电量为170千瓦时及以下,第二档电量为171千瓦时至260千瓦时,第三档电量为261千瓦时及以上,小颖家7月用电量为210千瓦时,交电费102.17元;8月用电量为180千瓦时,交电费86.36元.若第一档电价为x元/千瓦时,第二档电价为y元/千瓦时,则可得方程( )
A. B.
C. D.
3.二元一次方程x+3y=10的非负整数解共有( )对.
A.1 B.2 C.3 D.4
4.某车间有A,B,C型的生产线共12条,A,B,C型生产线每条生产线每小时的产量分别为4m,2m,m件,m为正整数.该车间准备增加3种类型的生产线共7条,其中B型生产线增加1条,受到限电限产的影响,每条生产线(包括之前的和新增的生产线)每小时的产量将减少4件.统计发现,增加生产线后,该车间每小时的总产量恰比增加生产线前减少10件,且A型生产线每小时的产量与三种类型生产线每小时的总产量之比为30:67.请问增加生产线后,该车间所有生产线每小时的总产量为 件.
5.某个“卡通玩具”自动售货机出售A、B、C三种玩具,A、B、C三种玩具的单价分别是3元/个、5元/个,6元/个,工作日期间,每天上货量是固定的,且能全部售出,其中,A玩具的数量(单位:个)是B玩具数量的2倍,B玩具的数量(单位:个)是C玩具数量的2倍.某个周六,A、B、C三种玩具的上货量分别比一个工作日的上货量增加了50%,70%、50%,且全部售出.但是由于软件出错,发生了一起错单(即消费者按某种玩具一个的价格投币,但是取得了另一种玩具1个),结果这个周六的销售收入比一个工作日的销售收入多了958元,则这个“卡通玩具”自动售货机一个工作日的销售收入是 元.
6.端午节有吃粽子的习惯,某商店购进肉粽、蛋黄粽、豆沙粽的数量之比为9:15:2.为促进销售,将全部粽子包装成A、B、C三种礼盒.礼盒A有2个肉粽、4个蛋黄粽;礼盒B有1个肉粽、3个蛋黄粽、1个豆沙粽;礼盒C有4个肉粽、2个豆沙粽.则礼盒A、礼盒B、礼盒C的盒数之比为 .
7.关于x、y的方程2x+ay=7仅有一组正整数解,则满足条件的正整数a的值为 .
8.一个油罐有进油龙头P和出油龙头Q.油罐空时,同时打开P、Q,4小时可注满油罐.油罐满时,先打开Q,12小时后关上;接着打开P,2小时后关上,此时油罐未满;再打开Q,5小时后油罐恰好流空.那么P的流量是Q的流量的 倍.
9.某校运动会在400米环形跑道上进行10000米比赛,甲、乙两运动员同时起跑后,乙速超过甲速,在第15分钟时甲加快速度,在第18分钟时甲追上乙并且开始超过乙,在第23分钟时,甲再次追上乙,而在第23分50秒时,甲到达终点,那么乙跑完全程所用的时间是 分钟.
10.医院用甲、乙两种原料为手术后的病人配制营养品,每克甲种原料含0.5单位的蛋白质和1单位铁质,每克乙种原料含0.7单位的蛋白质和0.4单位铁质.若病人每餐需要35单位的蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰能满足病人的需要?
11.阅读理解:
对于任意一个三位数正整数m(各个数位上的数字互不相同且都不为零),将m三个数位上的数字交换顺序,可以得到5个不同的数,把这6个数的和与111的商记为m的星河数T(m).例如m=234,可以得到243、324、342、423、432这5个不同的数,这6个数的和为234+243+324+342+423+432=1998,因为1998÷111=18,所以234的星河数T(234)=18.
(1)计算T(169)的值;
(2)若p和q都是各个数位上的数字互不相同且都不为零的三位正整数,p的十位和个位上的数字分别是6和3,3和7分别是q的百位和个位上的数字,且p的百位上的数字比q的十位上的数字大3.若15T(p)+17T(q)=828,求p和q的值.
12.平价商场经销的甲,乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)求甲种商品每件的进价;(利润率=×100%)
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元旦”期间,该商场只对乙种商品进行如表的优惠促销活动:
打折前一次性购物总金额 优惠措施
少于等于480元 不优惠
超过480元,但不超过680元 其中480元不打折,超过480元的部分给予6折优惠
超过680元 按购物总额给予7.5折优惠
按表的优惠条件,若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?
13.若关于x,y的方程组有非负数整数解,求正整数m.
14.如果一个三位数满足各位数字都不为0,且个位数字比十位数字大1,则称这个三位数为“圆梦数”,若m、n都是“圆梦数”,将组成m的各位数字中最大的数字作为两位数p的十位数字,组成n的各位数字中最大的数字作为两位数p的个位数字,再将组成m的各位数字中最小的数字作为另一个两位数q的十位数字,组成n的各位数字中最小的数字作为两位数q的个位数字,所得的这两个两位数p、q之和记为F(m,n).
例如:
∵5+1=6,2+1=3,∴556和923都是“圆梦数”,∴F(556,923)=69+52=121;
∵1+1=2,8+1=9,∴212和689都是“圆梦数”,∴F(212,689)=29+16=45.
(1)计算:F(767,634);F(978,445);
(2)若s和t都是“圆梦数”,其中s=500+10x+y,t=210+100a+b(1≤x≤8,0≤a≤7,且x、a都是整数),规定:K(s,t)=|s﹣t|,当F(s,312)﹣F(t,678)=20时,求K(s,t)的最大值.
15.某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片 张,正方形铁片 张;
(2)现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成3个长方形铁片或4个正方形铁片,也可以将一张铁板裁出1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒?
16.阅读材料:
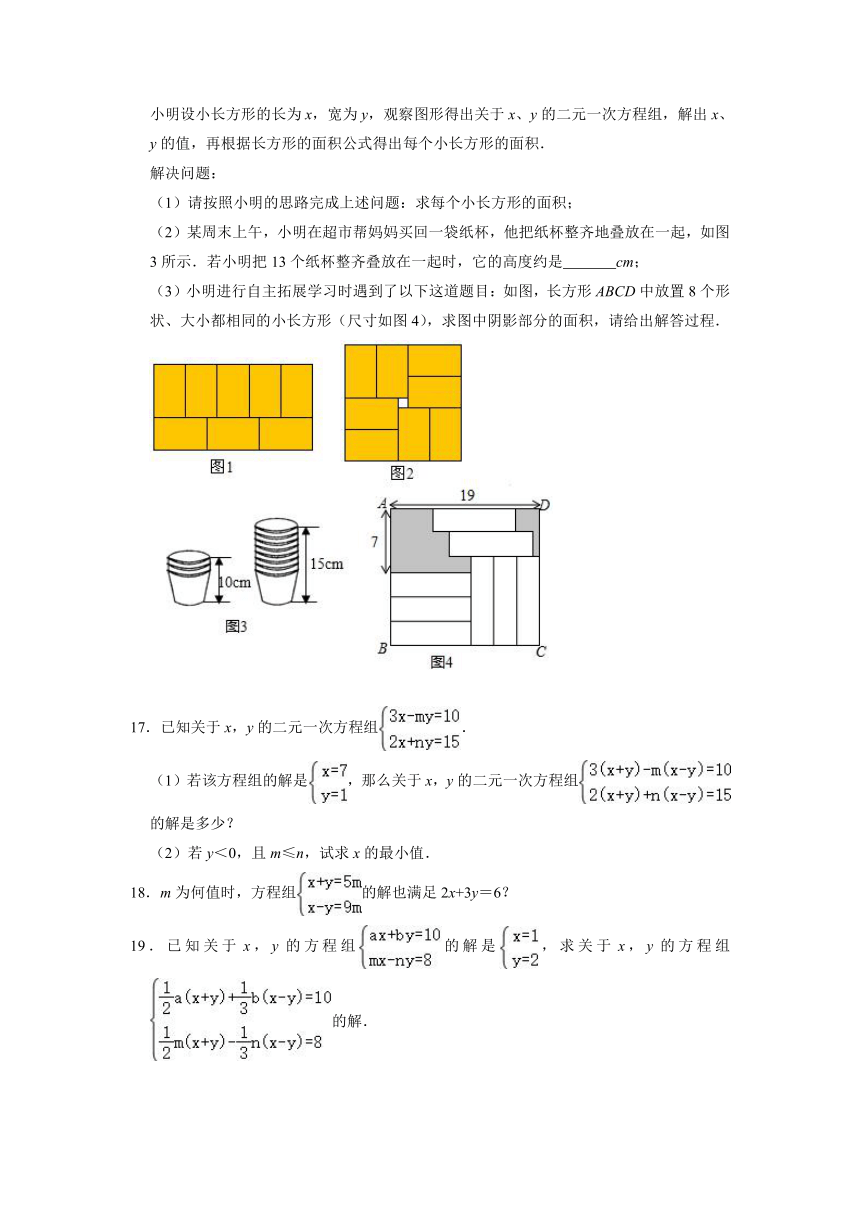
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是 cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.
17.已知关于x,y的二元一次方程组.
(1)若该方程组的解是,那么关于x,y的二元一次方程组的解是多少?
(2)若y<0,且m≤n,试求x的最小值.
18.m为何值时,方程组的解也满足2x+3y=6?
19.已知关于x,y的方程组的解是,求关于x,y的方程组的解.
20.已知关于x,y的方程组的解为满足x+y=4,求a的值.
21.阅读理解题:
阅读例子:已知:关于x、y的方程组的解是,求关于x、y的方程组的解.
解:方程组可化为
∵方程组的解是,
∴ ∴
∴方程组的解是
通过对上面材料的认真阅读后,解方程组:
已知:关于x、y的方程组的解是,求关于x、y的方程组的解.
22.小红和小丽对问题“若方程组的解是,求方程组的解”提出各自的想法.小红说:“这个题目好象条件不够,不能求解”;小丽说:“能不能把第二个方程组的两个方程的两边都除以5,通过整体代换的方法来解决”.参考他们的讨论,你认为这个题目应该怎样求解呢?
23.4月14日青海省玉树发生了7.1级大地震,驻军某部(位于距玉树县城结古镇91公里处的上拉秀镇)接到上级命令,须火速前往结古镇救援.已知该部有120名官兵,且步行的速度为每小时10公里,现仅有一辆时速为80公里的卡车,可乘坐40人,请你设计一个乘车兼步行方案,使该部120人能在最短时间内赶往重灾区结古镇救援.其中中途换车(上、下车)的时间均忽略不计,最快多少时间可以赶到?(可用分数表示)
参考答案
1.解:①将a=1代入原方程组,得 解得
将x=3,y=0,a=1代入方程x+y=2a+1的左右两边,
左边=3,右边=3,
当a=1时,方程组的解也是x+y=2a+1的解;
②解原方程组,得
若x,y是互为相反数,则x+y=0,
即2a+1+2﹣2a=0,方程无解.
无论a取何值,x,y的值不可能是互为相反数;
③∵x+y=2a+1+2﹣2a=3
∴x、y为自然数的解有,,,.
④∵2x+y=8,∴2(2a+1)+2﹣2a=8,
解得a=2.
故选:D.
2.解:小颖家7月电费:170x+(210﹣170)y=102.17,①
小颖家8月电费:170x+(180﹣170)y=86.36,②
①和②联立可得方程组.
故选:C.
3.解:∵x+3y=10,
∴x=10﹣3y,
∵x、y都是非负整数,
∴y=0时,x=10;
y=1时,x=7;
y=2时,x=4;
y=3时,x=1.
∴二元一次方程x+3y=10的非负整数解共有4对.
故选:D.
4.解:设增加生产线前A,B,C型生产线各有x、y、z条,增加生产线后A型增加a条,则C型增加(7﹣1﹣a)即(6﹣a)条,
由题意可得:
4mx+2my+mz=(x+a)(4m﹣4)+(y+1)(2m﹣4)+(z+6﹣a)(m﹣4)+10,
整理得:
3ma+8m=18+4(x+y+z),
由题意得:x+y+z=12,
代入上式整理可得:
m=,
又因为m是正整数,
所以3a+8的值可能为1、2、3、6、11、22、33,
结合0≤a≤6且a为正数,
可得3a+8=11,即a=1,
所以m=6,
所以增加生产线后A型增加1条生产线,B型增加1条生产线,C型增加5条生产线,
且增加生产线后A,B,C型生产线的每小时产量分别为(4m﹣4)(件)、(2m﹣4)(件)、(m﹣4)(件),
即增加生产线后A,B,C型生产线的每小时产量分别为20(件)、8(件)、2(件),
再由A型生产线每小时的产量与三种类型生产线每小时的总产量之比为30:67,
可得=,
化简分式方程得:1340x+1340=600x+600+240y+240+60z+300,
移项、合并同类项得:74x+20=24y+6z,
而由x+y+z=12得:x=12﹣y﹣z,
代入上式得:74(12﹣y﹣z)+20=24y+6z,
整理得:z=,
因为x、y、z均为非负整数,
所以454﹣49y一定能被整除,
所以454﹣49y的个位数字一定是0,
即49y的个位数字一定是4,
所以y=6(条),
那么z=4(条),
随即可得x=2(条),
再次检验当x、y、z分别为2、6、4时,以上分式均成立.
最后计算增加生产线后该车间生产线每小时总产量为:
20(2+1)+8(6+1)+2(4+5)=134(件).
故答案为:134.
5.解:工作日期间C玩具的数量为x个,则B玩具的数量为2x个,A玩具的数量为4x个,
∴工作日期间一天的销售收入为:12x+10x+6x=28x元,
周六C玩具的数量为1.5x个,则B玩具的数量为3.4x个,A玩具的数量为6x个,
∴周六销售销售收入为:18x+17x+9x=44x元,
∴周六销售收入与工作日期间一天销售收入的差为:44x﹣28x=16x元,
由于发生一起错单,收入的差为958元,
∴958加减一个玩具的差价一定是16的整数倍,
又∵958÷16=59……14(元),
∴付款是多14元或少2元,
∴这起错单发生在A、B玩具上(A、B的差价为2元),且是消费者付A玩具的钱,取走的是B玩具,
于是有:16x﹣(5﹣3)=958,
解得:x=60,
工作日期间一天的销售收入为:60×28=1680元,
故答案为:1680.
6.解:设该商店购进肉粽、蛋黄粽、豆沙粽的数量分别为9x个、15x个、2x个,礼盒A、礼盒B、礼盒C的盒数分别为a盒、b盒、c盒.
由题意,可得:
解得:
∴a:b:c=3x:x:=6:2:1.
故答案为:6:2:1.
7.解:2x+ay=7,
ay=7﹣2x,
①当x=1时,7﹣2x=5,
∴ay=5,
∴a=1,y=5(舍)或a=5,y=1,
②当x=2时,7﹣2x=3,
∴ay=3,
∴a=1,y=3(舍)或a=3,y=1,
③当x=3时,7﹣2x=1,
∴ay=1,
∴a=1,y=1(舍),
综上,满足条件的正整数a的值为5或3,
故答案为:5或3.
8.解:设P的工作效率为x,Q的工作效率为y,依题意得
①,
解得y=(与Q的工作效率不大于不相符,舍去);
②,
解得,
∴x÷y=倍,
故答案为倍.
9.解:设出发时甲速度为a米/分,乙速度为b米/分.第15分钟甲提高的速度为x米/分,
所以第15分钟后甲的速度是(a+x)米/分.
由题意得,
由①÷②得b﹣a=16(米/分),那么x=96米/分
将x代入③得 a=384米/分
∴b=400米/分.
∴乙跑完全程所用的时间==25(分).
故答案为25.
10.解:设每餐需甲原料x克,乙原料y克,
根据题意可列方程组
解得:.
答:每餐需甲种原料28克,乙种原料30克.
11.解:(1)T(169)=(169+196+619+691+916+961)÷111=32,
(2)设p=100x+63,q=307+10y,则y=x﹣3,
∴T(p)=(100x+63+100x+36+306+10x+360+x+603+10x+630+x)÷111=18+2x,
T(q)=(100y+37+100y+73+307+10y+370+y+703+10y+730+y)÷111=20+2y=20+2(x﹣3)=14+2x,
∵15T(p)+17T(q)=828,
∴15×(18+2x)+17×(14+2x)=828,
解得:x=5,y=2,
故:p=563,q=327.
12.解:(1)设甲种商品的进价为a元,则
98﹣a=40%a.
解得a=70.
答:甲种商品的进价为70元;
(2)设该商场购进甲种商品x件,根据题意可得:
70x+80(50﹣x)=3800,
解得:x=20;
乙种商品:50﹣20=30(件).
答:该商场购进甲种商品20件,乙种商品30件.
(3)设小华在该商场购买乙种商品b件,
根据题意,得
①当过480元,但不超过680元时,480+(128b﹣480)×0.6=576,
解得b=5.
②当超过680元时,128b×0.75=576,
解得b=6.
答:小华在该商场购买乙种商品5或6件.
13.解:解方程组得,,
∵关于x,y的方程组有非负数整数解,
∴m+1=4或2或1,
∴m=3或1或0(舍去),
答:正整数m为1、3.
14.解:(1)∵6+1=7,3+1=4,
∴767和634都是“圆梦数”,
∴F(767,634)=76+63=139;
∵7+1=8,4+1=5,
∴978和445都是“圆梦数”,
∴F(978,445)=95+74=169.
(2)∵s和t都是“圆梦数”,其中s=500+10x+y,t=210+100a+b(1≤x≤8,0≤a≤7,且x、a都是整数),
∴y=x+1,b=1+1=2,
∵K(s,t)=|s﹣t|,
∴K(s,t)=|500+10x+x+1﹣210﹣100a﹣2|=|11x﹣100a+289|,
①当x≥5时,有F(s,321)=10y+3+51=10y+54=10(x+1)+54=10x+64,
F(t,678)=10(a+2)+8+16=10a+44,
∵F(s,312)﹣F(t,678)=20,
∴10x+64﹣10a﹣44=20,
∴x=a,
∵K(s,t)=|11x﹣100a+289|,
∴k(s,t)=|11x﹣100x+289|=|289﹣89x|,
∵1≤x≤8,0≤a≤7,x=a,
∴5≤x≤7,
∴当x=7时,k(s,t)有最大值为:k(s,t)=|289﹣89×7|=334;
②当x<5时,有F(s,312)=53+10x+1=10x+54,
F(t,678)=10(a+2)+8+16=10a+44,
∵F(s,312)﹣F(t,678)=20,
∴10x+54﹣10a﹣44=20,
∴x﹣1=a,
∵K(s,t)=|11x﹣100a+289|,
∴k(s,t)=|11x﹣100(x﹣1)+289|=|389﹣89x|,
∵1≤x≤4,
∴当x=1时,k(s,t)有最大值为:k(s,t)=|389﹣89×1|=300;
∵300<334,
∴k(s,t)有最大值为334.
15.解:(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片7张,正方形铁片3张;
(2)设加工的竖式铁容器有x个,横式铁容器有y个,根据题意得,
解得
答:竖式铁容器加工100个,横式铁容器加工538个;
(3)设做长方形铁片的铁板为m块,做正方形铁片的铁板为n块,
依题意,得:,
解得:.
∵在这35块铁板中,25块做长方形铁片可做25×3=75(张),9块做正方形铁片可做9×4=36(张),剩下1块可裁出1张长方形铁片和2张正方形铁片,
∴共做长方形铁片75+1=76(张),正方形铁片36+2=38(张),
∴可做铁盒76÷4=19(个).
答:最多可以加工成19个铁盒.
16.解:(1)设小长方形的长为x,宽为y,
根据题意得:,解得:,
∴xy=10×6=60.
故每个小长方形的面积为60;
(2)设每两个纸杯叠放在一起比单独的一个纸杯增高xcm,单独一个纸杯的高度为ycm,
则,解得,
则12x+y=12×1+8=20.
即小明把13个纸杯整齐叠放在一起时,它的高度约是20cm.
(3)设小长方形的长为x,宽为y,根据题意得
,
解得,
∴S阴影=19×(7+3×3)﹣8×10×3=64.
故答案为:64.
17.解:(1)∵二元一次方程组的解是,
∴,解得:;
(2),
由①得:m=,
由②得:n=,
∵m≤n,
∴≤,
∵y<0,
∴3x﹣10≥15﹣2x,
x≥5,
∴x的最小值是5.
18.解:,
①+②得:2x=14m,
x=7m,
①﹣②得:2y=﹣4m,
y=﹣2m,
把x=7m,y=﹣2m代入2x+3y=6中得:14m﹣6m=6,
8m=6,
m=.
19.解:方程组变形为,
∵关于x,y的方程组的解是,
∴所求的方程组中,
整理得,,
解得,
即所求方程组的解是.
20.解:由,
①+②得,5x+5y=3a+2,
把x+y=4代入,
得,3a+2=20,
∴a=6.
21.解:方程组可化为,
∵方程组的解是,
∴,
∴.
∴方程组的解是.
22.解:将方程组两边同时除以5,原方程组化为
,
方程组的解是,
∴,
解得.
23.解:要使所用时间最短,卡车只能一直不停地往返载人行进,没有乘车的人也一直不停地向目的地行进,最后使120人同时到达结古镇,由于每车只能乘坐40人,因此将120人分成三组,安排乘车和步行如图所示:
其中图中箭头路线是汽车往返路线,
易知AE=CF=DB,AC=CD=EF=FB,
设AE=CF=DB=x(公里),AC=CD=EF=FB=y(公里),
由题意知:第一组乘车AE+步行EB=全程AB,
汽车AE+EC所用时间与步行AC所用时间相等,
∴,
解得:,
则全部由上接秀镇赶到玉树县城所用最短时间为:(小时)(8分).
答:最快3小时可以赶到.
1.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;④若2x+y=8,则a=2.正确的有几个( )
A.1 B.2 C.3 D.4
2.太原市城乡居民用电价格按用电需求分为三个档次,电价分档递增:第一档电量为170千瓦时及以下,第二档电量为171千瓦时至260千瓦时,第三档电量为261千瓦时及以上,小颖家7月用电量为210千瓦时,交电费102.17元;8月用电量为180千瓦时,交电费86.36元.若第一档电价为x元/千瓦时,第二档电价为y元/千瓦时,则可得方程( )
A. B.
C. D.
3.二元一次方程x+3y=10的非负整数解共有( )对.
A.1 B.2 C.3 D.4
4.某车间有A,B,C型的生产线共12条,A,B,C型生产线每条生产线每小时的产量分别为4m,2m,m件,m为正整数.该车间准备增加3种类型的生产线共7条,其中B型生产线增加1条,受到限电限产的影响,每条生产线(包括之前的和新增的生产线)每小时的产量将减少4件.统计发现,增加生产线后,该车间每小时的总产量恰比增加生产线前减少10件,且A型生产线每小时的产量与三种类型生产线每小时的总产量之比为30:67.请问增加生产线后,该车间所有生产线每小时的总产量为 件.
5.某个“卡通玩具”自动售货机出售A、B、C三种玩具,A、B、C三种玩具的单价分别是3元/个、5元/个,6元/个,工作日期间,每天上货量是固定的,且能全部售出,其中,A玩具的数量(单位:个)是B玩具数量的2倍,B玩具的数量(单位:个)是C玩具数量的2倍.某个周六,A、B、C三种玩具的上货量分别比一个工作日的上货量增加了50%,70%、50%,且全部售出.但是由于软件出错,发生了一起错单(即消费者按某种玩具一个的价格投币,但是取得了另一种玩具1个),结果这个周六的销售收入比一个工作日的销售收入多了958元,则这个“卡通玩具”自动售货机一个工作日的销售收入是 元.
6.端午节有吃粽子的习惯,某商店购进肉粽、蛋黄粽、豆沙粽的数量之比为9:15:2.为促进销售,将全部粽子包装成A、B、C三种礼盒.礼盒A有2个肉粽、4个蛋黄粽;礼盒B有1个肉粽、3个蛋黄粽、1个豆沙粽;礼盒C有4个肉粽、2个豆沙粽.则礼盒A、礼盒B、礼盒C的盒数之比为 .
7.关于x、y的方程2x+ay=7仅有一组正整数解,则满足条件的正整数a的值为 .
8.一个油罐有进油龙头P和出油龙头Q.油罐空时,同时打开P、Q,4小时可注满油罐.油罐满时,先打开Q,12小时后关上;接着打开P,2小时后关上,此时油罐未满;再打开Q,5小时后油罐恰好流空.那么P的流量是Q的流量的 倍.
9.某校运动会在400米环形跑道上进行10000米比赛,甲、乙两运动员同时起跑后,乙速超过甲速,在第15分钟时甲加快速度,在第18分钟时甲追上乙并且开始超过乙,在第23分钟时,甲再次追上乙,而在第23分50秒时,甲到达终点,那么乙跑完全程所用的时间是 分钟.
10.医院用甲、乙两种原料为手术后的病人配制营养品,每克甲种原料含0.5单位的蛋白质和1单位铁质,每克乙种原料含0.7单位的蛋白质和0.4单位铁质.若病人每餐需要35单位的蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰能满足病人的需要?
11.阅读理解:
对于任意一个三位数正整数m(各个数位上的数字互不相同且都不为零),将m三个数位上的数字交换顺序,可以得到5个不同的数,把这6个数的和与111的商记为m的星河数T(m).例如m=234,可以得到243、324、342、423、432这5个不同的数,这6个数的和为234+243+324+342+423+432=1998,因为1998÷111=18,所以234的星河数T(234)=18.
(1)计算T(169)的值;
(2)若p和q都是各个数位上的数字互不相同且都不为零的三位正整数,p的十位和个位上的数字分别是6和3,3和7分别是q的百位和个位上的数字,且p的百位上的数字比q的十位上的数字大3.若15T(p)+17T(q)=828,求p和q的值.
12.平价商场经销的甲,乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)求甲种商品每件的进价;(利润率=×100%)
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元旦”期间,该商场只对乙种商品进行如表的优惠促销活动:
打折前一次性购物总金额 优惠措施
少于等于480元 不优惠
超过480元,但不超过680元 其中480元不打折,超过480元的部分给予6折优惠
超过680元 按购物总额给予7.5折优惠
按表的优惠条件,若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?
13.若关于x,y的方程组有非负数整数解,求正整数m.
14.如果一个三位数满足各位数字都不为0,且个位数字比十位数字大1,则称这个三位数为“圆梦数”,若m、n都是“圆梦数”,将组成m的各位数字中最大的数字作为两位数p的十位数字,组成n的各位数字中最大的数字作为两位数p的个位数字,再将组成m的各位数字中最小的数字作为另一个两位数q的十位数字,组成n的各位数字中最小的数字作为两位数q的个位数字,所得的这两个两位数p、q之和记为F(m,n).
例如:
∵5+1=6,2+1=3,∴556和923都是“圆梦数”,∴F(556,923)=69+52=121;
∵1+1=2,8+1=9,∴212和689都是“圆梦数”,∴F(212,689)=29+16=45.
(1)计算:F(767,634);F(978,445);
(2)若s和t都是“圆梦数”,其中s=500+10x+y,t=210+100a+b(1≤x≤8,0≤a≤7,且x、a都是整数),规定:K(s,t)=|s﹣t|,当F(s,312)﹣F(t,678)=20时,求K(s,t)的最大值.
15.某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片 张,正方形铁片 张;
(2)现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成3个长方形铁片或4个正方形铁片,也可以将一张铁板裁出1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒?
16.阅读材料:
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是 cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.
17.已知关于x,y的二元一次方程组.
(1)若该方程组的解是,那么关于x,y的二元一次方程组的解是多少?
(2)若y<0,且m≤n,试求x的最小值.
18.m为何值时,方程组的解也满足2x+3y=6?
19.已知关于x,y的方程组的解是,求关于x,y的方程组的解.
20.已知关于x,y的方程组的解为满足x+y=4,求a的值.
21.阅读理解题:
阅读例子:已知:关于x、y的方程组的解是,求关于x、y的方程组的解.
解:方程组可化为
∵方程组的解是,
∴ ∴
∴方程组的解是
通过对上面材料的认真阅读后,解方程组:
已知:关于x、y的方程组的解是,求关于x、y的方程组的解.
22.小红和小丽对问题“若方程组的解是,求方程组的解”提出各自的想法.小红说:“这个题目好象条件不够,不能求解”;小丽说:“能不能把第二个方程组的两个方程的两边都除以5,通过整体代换的方法来解决”.参考他们的讨论,你认为这个题目应该怎样求解呢?
23.4月14日青海省玉树发生了7.1级大地震,驻军某部(位于距玉树县城结古镇91公里处的上拉秀镇)接到上级命令,须火速前往结古镇救援.已知该部有120名官兵,且步行的速度为每小时10公里,现仅有一辆时速为80公里的卡车,可乘坐40人,请你设计一个乘车兼步行方案,使该部120人能在最短时间内赶往重灾区结古镇救援.其中中途换车(上、下车)的时间均忽略不计,最快多少时间可以赶到?(可用分数表示)
参考答案
1.解:①将a=1代入原方程组,得 解得
将x=3,y=0,a=1代入方程x+y=2a+1的左右两边,
左边=3,右边=3,
当a=1时,方程组的解也是x+y=2a+1的解;
②解原方程组,得
若x,y是互为相反数,则x+y=0,
即2a+1+2﹣2a=0,方程无解.
无论a取何值,x,y的值不可能是互为相反数;
③∵x+y=2a+1+2﹣2a=3
∴x、y为自然数的解有,,,.
④∵2x+y=8,∴2(2a+1)+2﹣2a=8,
解得a=2.
故选:D.
2.解:小颖家7月电费:170x+(210﹣170)y=102.17,①
小颖家8月电费:170x+(180﹣170)y=86.36,②
①和②联立可得方程组.
故选:C.
3.解:∵x+3y=10,
∴x=10﹣3y,
∵x、y都是非负整数,
∴y=0时,x=10;
y=1时,x=7;
y=2时,x=4;
y=3时,x=1.
∴二元一次方程x+3y=10的非负整数解共有4对.
故选:D.
4.解:设增加生产线前A,B,C型生产线各有x、y、z条,增加生产线后A型增加a条,则C型增加(7﹣1﹣a)即(6﹣a)条,
由题意可得:
4mx+2my+mz=(x+a)(4m﹣4)+(y+1)(2m﹣4)+(z+6﹣a)(m﹣4)+10,
整理得:
3ma+8m=18+4(x+y+z),
由题意得:x+y+z=12,
代入上式整理可得:
m=,
又因为m是正整数,
所以3a+8的值可能为1、2、3、6、11、22、33,
结合0≤a≤6且a为正数,
可得3a+8=11,即a=1,
所以m=6,
所以增加生产线后A型增加1条生产线,B型增加1条生产线,C型增加5条生产线,
且增加生产线后A,B,C型生产线的每小时产量分别为(4m﹣4)(件)、(2m﹣4)(件)、(m﹣4)(件),
即增加生产线后A,B,C型生产线的每小时产量分别为20(件)、8(件)、2(件),
再由A型生产线每小时的产量与三种类型生产线每小时的总产量之比为30:67,
可得=,
化简分式方程得:1340x+1340=600x+600+240y+240+60z+300,
移项、合并同类项得:74x+20=24y+6z,
而由x+y+z=12得:x=12﹣y﹣z,
代入上式得:74(12﹣y﹣z)+20=24y+6z,
整理得:z=,
因为x、y、z均为非负整数,
所以454﹣49y一定能被整除,
所以454﹣49y的个位数字一定是0,
即49y的个位数字一定是4,
所以y=6(条),
那么z=4(条),
随即可得x=2(条),
再次检验当x、y、z分别为2、6、4时,以上分式均成立.
最后计算增加生产线后该车间生产线每小时总产量为:
20(2+1)+8(6+1)+2(4+5)=134(件).
故答案为:134.
5.解:工作日期间C玩具的数量为x个,则B玩具的数量为2x个,A玩具的数量为4x个,
∴工作日期间一天的销售收入为:12x+10x+6x=28x元,
周六C玩具的数量为1.5x个,则B玩具的数量为3.4x个,A玩具的数量为6x个,
∴周六销售销售收入为:18x+17x+9x=44x元,
∴周六销售收入与工作日期间一天销售收入的差为:44x﹣28x=16x元,
由于发生一起错单,收入的差为958元,
∴958加减一个玩具的差价一定是16的整数倍,
又∵958÷16=59……14(元),
∴付款是多14元或少2元,
∴这起错单发生在A、B玩具上(A、B的差价为2元),且是消费者付A玩具的钱,取走的是B玩具,
于是有:16x﹣(5﹣3)=958,
解得:x=60,
工作日期间一天的销售收入为:60×28=1680元,
故答案为:1680.
6.解:设该商店购进肉粽、蛋黄粽、豆沙粽的数量分别为9x个、15x个、2x个,礼盒A、礼盒B、礼盒C的盒数分别为a盒、b盒、c盒.
由题意,可得:
解得:
∴a:b:c=3x:x:=6:2:1.
故答案为:6:2:1.
7.解:2x+ay=7,
ay=7﹣2x,
①当x=1时,7﹣2x=5,
∴ay=5,
∴a=1,y=5(舍)或a=5,y=1,
②当x=2时,7﹣2x=3,
∴ay=3,
∴a=1,y=3(舍)或a=3,y=1,
③当x=3时,7﹣2x=1,
∴ay=1,
∴a=1,y=1(舍),
综上,满足条件的正整数a的值为5或3,
故答案为:5或3.
8.解:设P的工作效率为x,Q的工作效率为y,依题意得
①,
解得y=(与Q的工作效率不大于不相符,舍去);
②,
解得,
∴x÷y=倍,
故答案为倍.
9.解:设出发时甲速度为a米/分,乙速度为b米/分.第15分钟甲提高的速度为x米/分,
所以第15分钟后甲的速度是(a+x)米/分.
由题意得,
由①÷②得b﹣a=16(米/分),那么x=96米/分
将x代入③得 a=384米/分
∴b=400米/分.
∴乙跑完全程所用的时间==25(分).
故答案为25.
10.解:设每餐需甲原料x克,乙原料y克,
根据题意可列方程组
解得:.
答:每餐需甲种原料28克,乙种原料30克.
11.解:(1)T(169)=(169+196+619+691+916+961)÷111=32,
(2)设p=100x+63,q=307+10y,则y=x﹣3,
∴T(p)=(100x+63+100x+36+306+10x+360+x+603+10x+630+x)÷111=18+2x,
T(q)=(100y+37+100y+73+307+10y+370+y+703+10y+730+y)÷111=20+2y=20+2(x﹣3)=14+2x,
∵15T(p)+17T(q)=828,
∴15×(18+2x)+17×(14+2x)=828,
解得:x=5,y=2,
故:p=563,q=327.
12.解:(1)设甲种商品的进价为a元,则
98﹣a=40%a.
解得a=70.
答:甲种商品的进价为70元;
(2)设该商场购进甲种商品x件,根据题意可得:
70x+80(50﹣x)=3800,
解得:x=20;
乙种商品:50﹣20=30(件).
答:该商场购进甲种商品20件,乙种商品30件.
(3)设小华在该商场购买乙种商品b件,
根据题意,得
①当过480元,但不超过680元时,480+(128b﹣480)×0.6=576,
解得b=5.
②当超过680元时,128b×0.75=576,
解得b=6.
答:小华在该商场购买乙种商品5或6件.
13.解:解方程组得,,
∵关于x,y的方程组有非负数整数解,
∴m+1=4或2或1,
∴m=3或1或0(舍去),
答:正整数m为1、3.
14.解:(1)∵6+1=7,3+1=4,
∴767和634都是“圆梦数”,
∴F(767,634)=76+63=139;
∵7+1=8,4+1=5,
∴978和445都是“圆梦数”,
∴F(978,445)=95+74=169.
(2)∵s和t都是“圆梦数”,其中s=500+10x+y,t=210+100a+b(1≤x≤8,0≤a≤7,且x、a都是整数),
∴y=x+1,b=1+1=2,
∵K(s,t)=|s﹣t|,
∴K(s,t)=|500+10x+x+1﹣210﹣100a﹣2|=|11x﹣100a+289|,
①当x≥5时,有F(s,321)=10y+3+51=10y+54=10(x+1)+54=10x+64,
F(t,678)=10(a+2)+8+16=10a+44,
∵F(s,312)﹣F(t,678)=20,
∴10x+64﹣10a﹣44=20,
∴x=a,
∵K(s,t)=|11x﹣100a+289|,
∴k(s,t)=|11x﹣100x+289|=|289﹣89x|,
∵1≤x≤8,0≤a≤7,x=a,
∴5≤x≤7,
∴当x=7时,k(s,t)有最大值为:k(s,t)=|289﹣89×7|=334;
②当x<5时,有F(s,312)=53+10x+1=10x+54,
F(t,678)=10(a+2)+8+16=10a+44,
∵F(s,312)﹣F(t,678)=20,
∴10x+54﹣10a﹣44=20,
∴x﹣1=a,
∵K(s,t)=|11x﹣100a+289|,
∴k(s,t)=|11x﹣100(x﹣1)+289|=|389﹣89x|,
∵1≤x≤4,
∴当x=1时,k(s,t)有最大值为:k(s,t)=|389﹣89×1|=300;
∵300<334,
∴k(s,t)有最大值为334.
15.解:(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片7张,正方形铁片3张;
(2)设加工的竖式铁容器有x个,横式铁容器有y个,根据题意得,
解得
答:竖式铁容器加工100个,横式铁容器加工538个;
(3)设做长方形铁片的铁板为m块,做正方形铁片的铁板为n块,
依题意,得:,
解得:.
∵在这35块铁板中,25块做长方形铁片可做25×3=75(张),9块做正方形铁片可做9×4=36(张),剩下1块可裁出1张长方形铁片和2张正方形铁片,
∴共做长方形铁片75+1=76(张),正方形铁片36+2=38(张),
∴可做铁盒76÷4=19(个).
答:最多可以加工成19个铁盒.
16.解:(1)设小长方形的长为x,宽为y,
根据题意得:,解得:,
∴xy=10×6=60.
故每个小长方形的面积为60;
(2)设每两个纸杯叠放在一起比单独的一个纸杯增高xcm,单独一个纸杯的高度为ycm,
则,解得,
则12x+y=12×1+8=20.
即小明把13个纸杯整齐叠放在一起时,它的高度约是20cm.
(3)设小长方形的长为x,宽为y,根据题意得
,
解得,
∴S阴影=19×(7+3×3)﹣8×10×3=64.
故答案为:64.
17.解:(1)∵二元一次方程组的解是,
∴,解得:;
(2),
由①得:m=,
由②得:n=,
∵m≤n,
∴≤,
∵y<0,
∴3x﹣10≥15﹣2x,
x≥5,
∴x的最小值是5.
18.解:,
①+②得:2x=14m,
x=7m,
①﹣②得:2y=﹣4m,
y=﹣2m,
把x=7m,y=﹣2m代入2x+3y=6中得:14m﹣6m=6,
8m=6,
m=.
19.解:方程组变形为,
∵关于x,y的方程组的解是,
∴所求的方程组中,
整理得,,
解得,
即所求方程组的解是.
20.解:由,
①+②得,5x+5y=3a+2,
把x+y=4代入,
得,3a+2=20,
∴a=6.
21.解:方程组可化为,
∵方程组的解是,
∴,
∴.
∴方程组的解是.
22.解:将方程组两边同时除以5,原方程组化为
,
方程组的解是,
∴,
解得.
23.解:要使所用时间最短,卡车只能一直不停地往返载人行进,没有乘车的人也一直不停地向目的地行进,最后使120人同时到达结古镇,由于每车只能乘坐40人,因此将120人分成三组,安排乘车和步行如图所示:
其中图中箭头路线是汽车往返路线,
易知AE=CF=DB,AC=CD=EF=FB,
设AE=CF=DB=x(公里),AC=CD=EF=FB=y(公里),
由题意知:第一组乘车AE+步行EB=全程AB,
汽车AE+EC所用时间与步行AC所用时间相等,
∴,
解得:,
则全部由上接秀镇赶到玉树县城所用最短时间为:(小时)(8分).
答:最快3小时可以赶到.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
