2021-2022学年人教版八年级数学下册17.1勾股定理同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.1勾股定理同步达标测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览



文档简介
2021-2022学年人教版八年级数学下册《17-1勾股定理》同步达标测试题(附答案)
一.选择题(共10小题,满分30分)
1.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A.﹣1﹣ B.1﹣ C.﹣ D.﹣1+
2.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当AC=4,BC=2时,则阴影部分的面积为( )
A.4 B.4π C.8π D.8
3.若等腰三角形的腰长为10,底边长为12,则底边上的高为( )
A.6 B.7 C.8 D.9
4.若一直角三角形两边长分别为12和5,则第三边长为( )
A.13 B.13或 C.13或15 D.15
5.如图,在△ABC中,∠ABC=90°,AC=10,AB=8,若两阴影部分都是正方形,C、D、E在一条直线上,且它们的面积之比为1:3,则较大的正方形的面积( )
A.36 B.27 C.18 D.9
6.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3.若S1+S2+S3=60,则S2的值是( )
A.12 B.15 C.20 D.30
7.正方形的网格中,每个小正方形的边长为1,则网格中三角形ABC中,边长是无理数的边数是( )
A.0 B.1 C.2 D.3
8.在平面直角坐标系中,已知点P的坐标是(2,1),则以点O为圆心,OP长为半径的圆与x轴正半轴的交点A表示的数为( )
A.1 B.2 C. D.
9.如图,一个梯子斜靠在一竖直的墙AO上,测得AO=4m,若梯子的顶端沿墙下滑1m,这时梯子的底端也下滑1m,则梯子AB的长度为( )
A.5m B.6m C.3m D.7m
10.如图,牧童在A处放牛,牧童家在B处,A、B处距河岸DC的距离AC、BD的长分别为500m和700m,且C,D两点的距离为500m,天黑前牧童从A处将牛牵到河边饮水再回家,那么牧童最少要走的距离为( )
A.1000m B.1200m C.1300m D.1700m
二.填空题(共10小题,满分30分)
11.已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
12.如图,已知OA=OB,那么数轴上点A所表示的数是 .
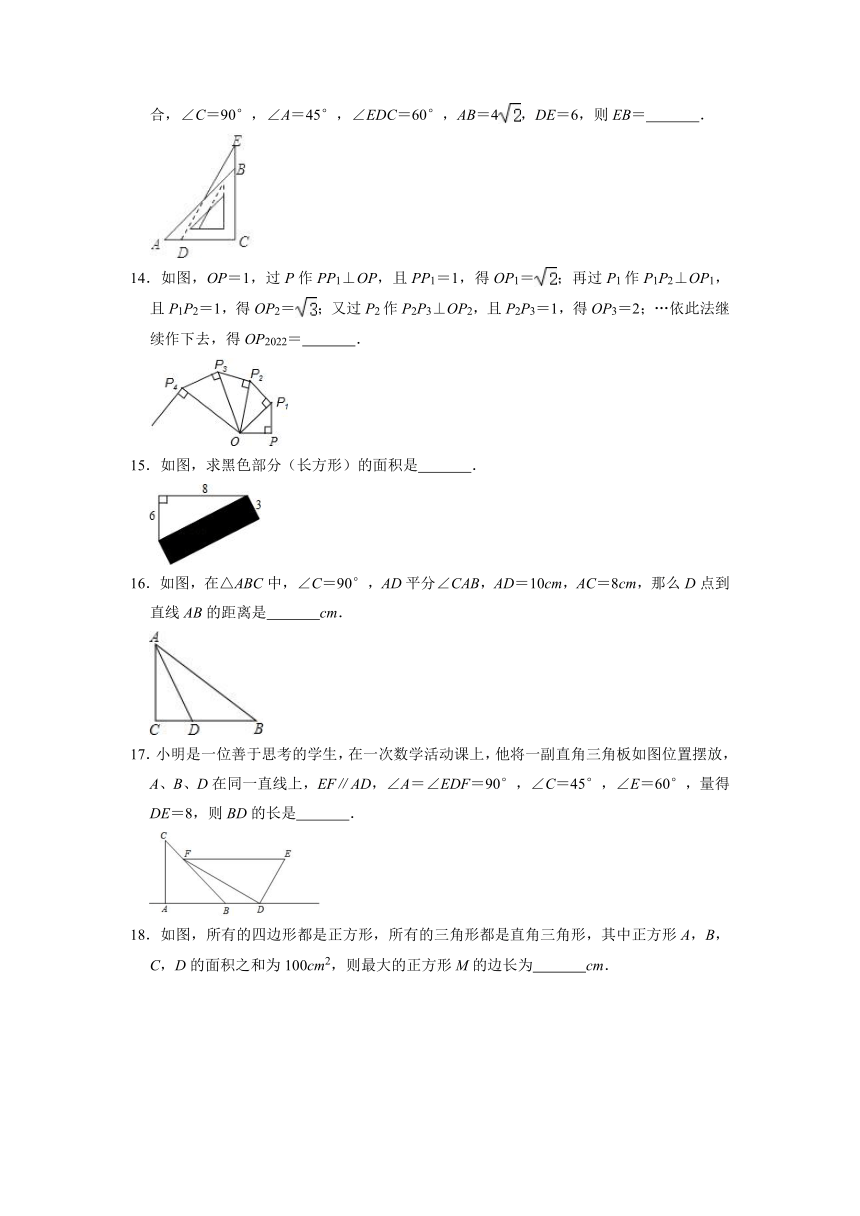
13.将一个含30°角的三角板和一个含45°角的三角板如图摆放,∠ACB与∠DCE完全重合,∠C=90°,∠A=45°,∠EDC=60°,AB=4,DE=6,则EB= .
14.如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2022= .
15.如图,求黑色部分(长方形)的面积是 .
16.如图,在△ABC中,∠C=90°,AD平分∠CAB,AD=10cm,AC=8cm,那么D点到直线AB的距离是 cm.
17.小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,则BD的长是 .
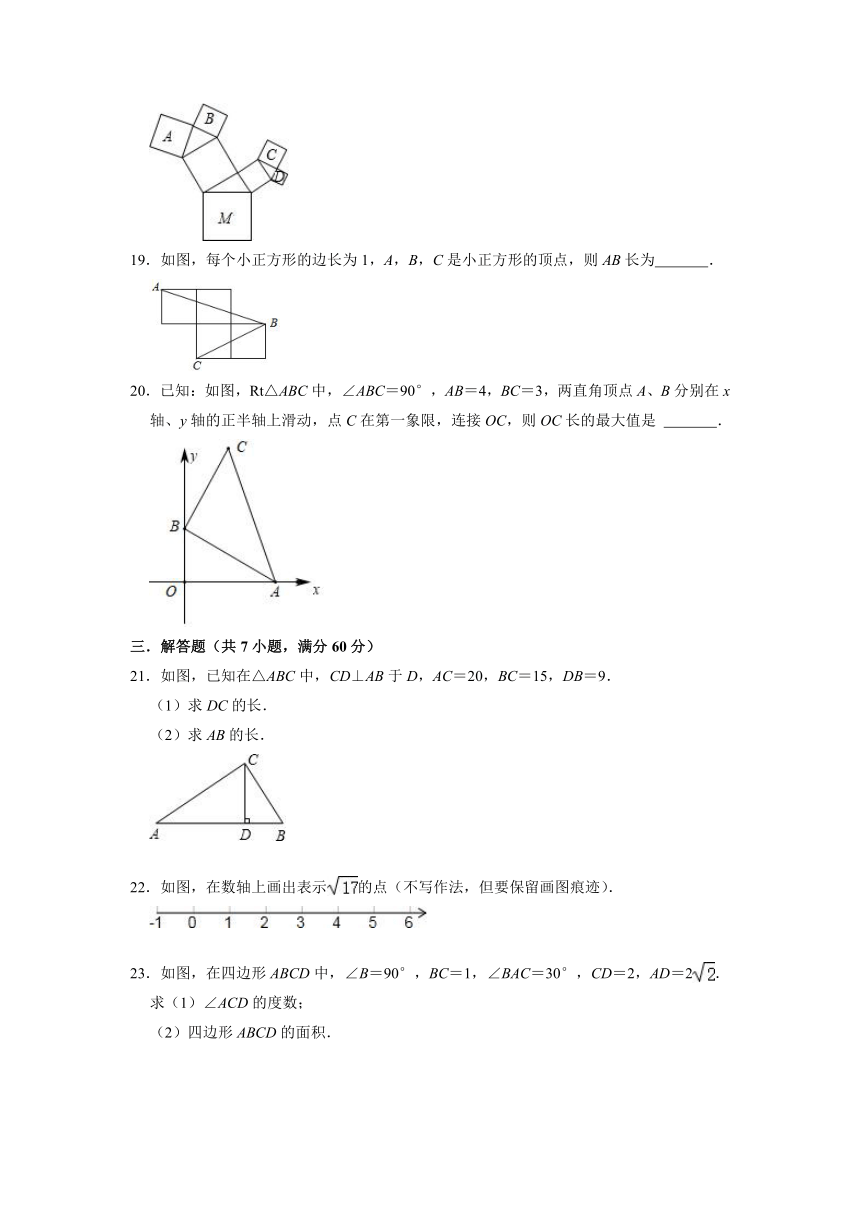
18.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中正方形A,B,C,D的面积之和为100cm2,则最大的正方形M的边长为 cm.
19.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则AB长为 .
20.已知:如图,Rt△ABC中,∠ABC=90°,AB=4,BC=3,两直角顶点A、B分别在x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则OC长的最大值是 .
三.解答题(共7小题,满分60分)
21.如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
(1)求DC的长.
(2)求AB的长.
22.如图,在数轴上画出表示的点(不写作法,但要保留画图痕迹).
23.如图,在四边形ABCD中,∠B=90°,BC=1,∠BAC=30°,CD=2,AD=2.
求(1)∠ACD的度数;
(2)四边形ABCD的面积.
24.如图,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求△BCD的面积.
25.如图,在Rt△ABD中,∠ABD=90°,AD=10,AB=8.在其右侧的同一个平面内作△BCD,使BC=8,CD=2.求证:AB∥DC.
26.如图,一个直径为12cm的杯子,在它的正中间竖直放一根小木棍,小木棍露出杯子外2cm,当小木棍倒向杯壁时(小木棍底端不动),小木棍顶端正好触到杯口,求小木棍长度.
27.如图所示,是一个三级台阶,它的每一级的长、宽、高分别为55cm,10cm,6cm,点A和点B是这个台阶的两个相对的端点,A点处有一只蚂蚁,那么这只蚂蚁从点A爬到点B的最短路程是多少?
参考答案
一.选择题(共10小题,满分30分)
1.解:如图,点A在以O为圆心,OB长为半径的圆上.
∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,
∴OA=OB=,
∴a=﹣1﹣.
故选:A.
2.解:由勾股定理得,AB2=AC2+BC2=20,
则阴影部分的面积=×AC×BC+×π×()2+×π×()2﹣×π×()2
=×2×4+×π××(AC2+BC2﹣AB2)
=4,
故选:A.
3.解:作底边上的高并设此高的长度为x,则根据勾股定理得:62+x2=102;
解得:x=8,
故选:C.
4.解:当12是斜边时,第三边是=;
当12是直角边时,第三边是=13.
故选:B.
5.解:设两个正方形的面积分别为a和3a,
∵∠ABC=90°,AC=10,AB=8,
∴BC2=AC2﹣AB2=102﹣82=36,
∵BD2+CD2=BC2,
∴a+3a=36,
∴a=9,
∴3a=27,
∴较大的正方形的面积为27,
故选:B.
6.解:设每个小直角三角形的面积为m,则S1=4m+S2,S3=S2﹣4m,
因为S1+S2+S3=60,
所以4m+S2+S2+S2﹣4m=60,
即3S2=60,
解得S2=20.
故选:C.
7.解:观察图形,应用勾股定理,得
AB==,
BC==,
AC==5,
边长是无理数的边数是2.
故选:C.
8.解:OP两点之间的距离=,P点沿O为圆心、为半径的圆与x轴正半轴的交点只有一个,即OP的长.
所以OP长为半径的圆与x轴正半轴的交点A表示的数为,
故选:D.
9.解:设BO=xm,
由题意得:AC=1m,BD=1m,AO=4m,
在Rt△AOB中,根据勾股定理得:AB2=AO2+OB2=42+x2,
在Rt△COD中,根据勾股定理得:CD2=CO2+OD2=(4﹣1)2+(x+1)2,
∴42+x2=(4﹣1)2+(x+1)2,
解得:x=3,
∴AB=5(m),
即梯子AB的长为5m,
故选:A.
10.解:作A点关于河岸的对称点A′,连接BA′交河岸与P,连接A′B′,连接PA,过A'作A'B'⊥BD于B',
则PB+PA=PB+PA′=BA′最短,故牧童应将马赶到河边的P地点.
∴B'D=A'C=CA=500m,
∴BB′=BD+BD′=700+500=1200(m),
∵A'B'=CD=500m,
∴BA'=1300(m).
即牧童至少要走的距离为1300m,
故选:C.
二.填空题(共10小题,满分30分)
11.解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP===3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM==3,
当P在M的左边时,CP=5﹣3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
12.解:由图可知,OC=2,作BC⊥OC,垂足为C,取BC=1,
故OB=OA===,
∵A在x的负半轴上,
∴数轴上点A所表示的数是﹣.
故答案为:﹣.
13.解:在Rt△ABC中,
∵AB=4,∠A=45°,
∴BC=4×=4
在Rt△EDC中,
∵∠EDC=60°,DE=6,
∴CE=DE sin∠EDC=6×=3
∴BE=CE﹣BC=3﹣4.
故填空答案:3﹣4.
14.解:∵OP=1,OP1=,OP2=,OP3==2,
∴OP4==,
…,
OP2022=.
故答案为:.
15.解:在直角三角形中,已知两直角边分别为6,8,
则斜边长=10,
根据矩形面积计算公式S=长×宽=3×10=30,
故答案为 30.
16.解:∵AD=10cm,AC=8cm
∴CD=6cm
∵AD平分∠CAB
∴D点到直线AB的距离=CD=6cm
17.解:作FH⊥AD于H,
在△DEF中,∠EDF=90°,∠E=60°,
∴∠DFE=30°,
∴EF=DE=16,
由勾股定理得,DF===8,
∵EF∥AD,
∴∠FDH=∠DFE=30°,
∴FH=DF=4,
由勾股定理得,DH==12,
在Rt△FBH中,∠ABC=∠C=45°,
∴BH=FH=4,
∴BD=DH﹣BH=12﹣4,
故答案为:12﹣4.
18.解:根据勾股定理的几何意义可知:
SA+SB=SE,
SC+SD=SF,
SE+SF=SM.
于是SM=SA+SB+SC+SD=100cm2.
则M的边长为10cm.
故答案为:10.
19.解:如图所示,由勾股定理知:AB==.
故答案是:.
20.解:取AB中点P,连接OP、CP,
则OP=BP=AB=2,
由勾股定理得,CP==,
利用三角形两边之和大于点三边可知:OC≤OP+PC=,OC的长的最大值为,
故答案为:.
三.解答题(共7小题,满分60分)
21.解:(1)∵CD⊥AB于D,且BC=15,BD=9,AC=20
∴∠CDA=∠CDB=90°
在Rt△CDB中,CD2+BD2=CB2,
∴CD2+92=152
∴CD=12;
(2)在Rt△CDA中,CD2+AD2=AC2
∴122+AD2=202
∴AD=16,
∴AB=AD+BD=16+9=25.
22.解:所画图形如下所示,其中点A即为所求.
23.(1)解:∵∠B=90°,∠BAC=30°,BC=1,
∴AC=2BC=2,
又CD=2,AD=2,
∴AC2+CD2=8,AD2=8,
∴AC2+CD2=AD2,
∴△ACD是直角三角形.
∴∠ACD=90°;
(2)解:∵AC=2,BC=1,
∴AB==,
∴四边形ABCD的面积=三角形ABC的面积+三角形ADC的面积==.
24.解:(1)∵∠A=90°,AB=9,AC=12
∴BC==15,
(2)∵BC=15,BD=8,CD=17
∴BC2+BD2=CD2
∴△BCD是直角三角形
∴S△BCD=×15×8=60.
25.证明:∵在Rt△ABD中,∠ABD=90°,AD=10,AB=8,
∴BD===6,
∵BC=8,CD=2,
∴62+(2)2=82,
∴△BDC是直角三角形,
∴∠BDC=90°,
∴∠ABD=∠BDC,
∴AB∥DC.
26.解:设杯子的高度是xcm,那么小木棍的高度是(x+2)cm,
∵杯子的直径为12cm,
∴杯子半径为6cm,
∴x2+62=(x+2)2,
即x2+36=x2+4x+4,
解得:x=8,
8+2=10(cm).
答:小木棍长10cm.
27.解:如图所示,将这个台阶展开成一个平面图形,则蚂蚁爬行的最短路程就是线段AB的长.
在Rt△ABC中,BC=55cm,AC=10+6+10+6+10+6=48(cm).
由勾股定理,得AB2=AC2+BC2=5329.
所以AB=73(cm).
因此,蚂蚁从点A爬到点B的最短路程是73cm.
一.选择题(共10小题,满分30分)
1.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A.﹣1﹣ B.1﹣ C.﹣ D.﹣1+
2.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当AC=4,BC=2时,则阴影部分的面积为( )
A.4 B.4π C.8π D.8
3.若等腰三角形的腰长为10,底边长为12,则底边上的高为( )
A.6 B.7 C.8 D.9
4.若一直角三角形两边长分别为12和5,则第三边长为( )
A.13 B.13或 C.13或15 D.15
5.如图,在△ABC中,∠ABC=90°,AC=10,AB=8,若两阴影部分都是正方形,C、D、E在一条直线上,且它们的面积之比为1:3,则较大的正方形的面积( )
A.36 B.27 C.18 D.9
6.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3.若S1+S2+S3=60,则S2的值是( )
A.12 B.15 C.20 D.30
7.正方形的网格中,每个小正方形的边长为1,则网格中三角形ABC中,边长是无理数的边数是( )
A.0 B.1 C.2 D.3
8.在平面直角坐标系中,已知点P的坐标是(2,1),则以点O为圆心,OP长为半径的圆与x轴正半轴的交点A表示的数为( )
A.1 B.2 C. D.
9.如图,一个梯子斜靠在一竖直的墙AO上,测得AO=4m,若梯子的顶端沿墙下滑1m,这时梯子的底端也下滑1m,则梯子AB的长度为( )
A.5m B.6m C.3m D.7m
10.如图,牧童在A处放牛,牧童家在B处,A、B处距河岸DC的距离AC、BD的长分别为500m和700m,且C,D两点的距离为500m,天黑前牧童从A处将牛牵到河边饮水再回家,那么牧童最少要走的距离为( )
A.1000m B.1200m C.1300m D.1700m
二.填空题(共10小题,满分30分)
11.已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
12.如图,已知OA=OB,那么数轴上点A所表示的数是 .
13.将一个含30°角的三角板和一个含45°角的三角板如图摆放,∠ACB与∠DCE完全重合,∠C=90°,∠A=45°,∠EDC=60°,AB=4,DE=6,则EB= .
14.如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2022= .
15.如图,求黑色部分(长方形)的面积是 .
16.如图,在△ABC中,∠C=90°,AD平分∠CAB,AD=10cm,AC=8cm,那么D点到直线AB的距离是 cm.
17.小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,则BD的长是 .
18.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中正方形A,B,C,D的面积之和为100cm2,则最大的正方形M的边长为 cm.
19.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则AB长为 .
20.已知:如图,Rt△ABC中,∠ABC=90°,AB=4,BC=3,两直角顶点A、B分别在x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则OC长的最大值是 .
三.解答题(共7小题,满分60分)
21.如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
(1)求DC的长.
(2)求AB的长.
22.如图,在数轴上画出表示的点(不写作法,但要保留画图痕迹).
23.如图,在四边形ABCD中,∠B=90°,BC=1,∠BAC=30°,CD=2,AD=2.
求(1)∠ACD的度数;
(2)四边形ABCD的面积.
24.如图,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求△BCD的面积.
25.如图,在Rt△ABD中,∠ABD=90°,AD=10,AB=8.在其右侧的同一个平面内作△BCD,使BC=8,CD=2.求证:AB∥DC.
26.如图,一个直径为12cm的杯子,在它的正中间竖直放一根小木棍,小木棍露出杯子外2cm,当小木棍倒向杯壁时(小木棍底端不动),小木棍顶端正好触到杯口,求小木棍长度.
27.如图所示,是一个三级台阶,它的每一级的长、宽、高分别为55cm,10cm,6cm,点A和点B是这个台阶的两个相对的端点,A点处有一只蚂蚁,那么这只蚂蚁从点A爬到点B的最短路程是多少?
参考答案
一.选择题(共10小题,满分30分)
1.解:如图,点A在以O为圆心,OB长为半径的圆上.
∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,
∴OA=OB=,
∴a=﹣1﹣.
故选:A.
2.解:由勾股定理得,AB2=AC2+BC2=20,
则阴影部分的面积=×AC×BC+×π×()2+×π×()2﹣×π×()2
=×2×4+×π××(AC2+BC2﹣AB2)
=4,
故选:A.
3.解:作底边上的高并设此高的长度为x,则根据勾股定理得:62+x2=102;
解得:x=8,
故选:C.
4.解:当12是斜边时,第三边是=;
当12是直角边时,第三边是=13.
故选:B.
5.解:设两个正方形的面积分别为a和3a,
∵∠ABC=90°,AC=10,AB=8,
∴BC2=AC2﹣AB2=102﹣82=36,
∵BD2+CD2=BC2,
∴a+3a=36,
∴a=9,
∴3a=27,
∴较大的正方形的面积为27,
故选:B.
6.解:设每个小直角三角形的面积为m,则S1=4m+S2,S3=S2﹣4m,
因为S1+S2+S3=60,
所以4m+S2+S2+S2﹣4m=60,
即3S2=60,
解得S2=20.
故选:C.
7.解:观察图形,应用勾股定理,得
AB==,
BC==,
AC==5,
边长是无理数的边数是2.
故选:C.
8.解:OP两点之间的距离=,P点沿O为圆心、为半径的圆与x轴正半轴的交点只有一个,即OP的长.
所以OP长为半径的圆与x轴正半轴的交点A表示的数为,
故选:D.
9.解:设BO=xm,
由题意得:AC=1m,BD=1m,AO=4m,
在Rt△AOB中,根据勾股定理得:AB2=AO2+OB2=42+x2,
在Rt△COD中,根据勾股定理得:CD2=CO2+OD2=(4﹣1)2+(x+1)2,
∴42+x2=(4﹣1)2+(x+1)2,
解得:x=3,
∴AB=5(m),
即梯子AB的长为5m,
故选:A.
10.解:作A点关于河岸的对称点A′,连接BA′交河岸与P,连接A′B′,连接PA,过A'作A'B'⊥BD于B',
则PB+PA=PB+PA′=BA′最短,故牧童应将马赶到河边的P地点.
∴B'D=A'C=CA=500m,
∴BB′=BD+BD′=700+500=1200(m),
∵A'B'=CD=500m,
∴BA'=1300(m).
即牧童至少要走的距离为1300m,
故选:C.
二.填空题(共10小题,满分30分)
11.解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP===3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM==3,
当P在M的左边时,CP=5﹣3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
12.解:由图可知,OC=2,作BC⊥OC,垂足为C,取BC=1,
故OB=OA===,
∵A在x的负半轴上,
∴数轴上点A所表示的数是﹣.
故答案为:﹣.
13.解:在Rt△ABC中,
∵AB=4,∠A=45°,
∴BC=4×=4
在Rt△EDC中,
∵∠EDC=60°,DE=6,
∴CE=DE sin∠EDC=6×=3
∴BE=CE﹣BC=3﹣4.
故填空答案:3﹣4.
14.解:∵OP=1,OP1=,OP2=,OP3==2,
∴OP4==,
…,
OP2022=.
故答案为:.
15.解:在直角三角形中,已知两直角边分别为6,8,
则斜边长=10,
根据矩形面积计算公式S=长×宽=3×10=30,
故答案为 30.
16.解:∵AD=10cm,AC=8cm
∴CD=6cm
∵AD平分∠CAB
∴D点到直线AB的距离=CD=6cm
17.解:作FH⊥AD于H,
在△DEF中,∠EDF=90°,∠E=60°,
∴∠DFE=30°,
∴EF=DE=16,
由勾股定理得,DF===8,
∵EF∥AD,
∴∠FDH=∠DFE=30°,
∴FH=DF=4,
由勾股定理得,DH==12,
在Rt△FBH中,∠ABC=∠C=45°,
∴BH=FH=4,
∴BD=DH﹣BH=12﹣4,
故答案为:12﹣4.
18.解:根据勾股定理的几何意义可知:
SA+SB=SE,
SC+SD=SF,
SE+SF=SM.
于是SM=SA+SB+SC+SD=100cm2.
则M的边长为10cm.
故答案为:10.
19.解:如图所示,由勾股定理知:AB==.
故答案是:.
20.解:取AB中点P,连接OP、CP,
则OP=BP=AB=2,
由勾股定理得,CP==,
利用三角形两边之和大于点三边可知:OC≤OP+PC=,OC的长的最大值为,
故答案为:.
三.解答题(共7小题,满分60分)
21.解:(1)∵CD⊥AB于D,且BC=15,BD=9,AC=20
∴∠CDA=∠CDB=90°
在Rt△CDB中,CD2+BD2=CB2,
∴CD2+92=152
∴CD=12;
(2)在Rt△CDA中,CD2+AD2=AC2
∴122+AD2=202
∴AD=16,
∴AB=AD+BD=16+9=25.
22.解:所画图形如下所示,其中点A即为所求.
23.(1)解:∵∠B=90°,∠BAC=30°,BC=1,
∴AC=2BC=2,
又CD=2,AD=2,
∴AC2+CD2=8,AD2=8,
∴AC2+CD2=AD2,
∴△ACD是直角三角形.
∴∠ACD=90°;
(2)解:∵AC=2,BC=1,
∴AB==,
∴四边形ABCD的面积=三角形ABC的面积+三角形ADC的面积==.
24.解:(1)∵∠A=90°,AB=9,AC=12
∴BC==15,
(2)∵BC=15,BD=8,CD=17
∴BC2+BD2=CD2
∴△BCD是直角三角形
∴S△BCD=×15×8=60.
25.证明:∵在Rt△ABD中,∠ABD=90°,AD=10,AB=8,
∴BD===6,
∵BC=8,CD=2,
∴62+(2)2=82,
∴△BDC是直角三角形,
∴∠BDC=90°,
∴∠ABD=∠BDC,
∴AB∥DC.
26.解:设杯子的高度是xcm,那么小木棍的高度是(x+2)cm,
∵杯子的直径为12cm,
∴杯子半径为6cm,
∴x2+62=(x+2)2,
即x2+36=x2+4x+4,
解得:x=8,
8+2=10(cm).
答:小木棍长10cm.
27.解:如图所示,将这个台阶展开成一个平面图形,则蚂蚁爬行的最短路程就是线段AB的长.
在Rt△ABC中,BC=55cm,AC=10+6+10+6+10+6=48(cm).
由勾股定理,得AB2=AC2+BC2=5329.
所以AB=73(cm).
因此,蚂蚁从点A爬到点B的最短路程是73cm.
