2021-2022学年人教版八年级数学下+17.2勾股定理的逆定理同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下+17.2勾股定理的逆定理同步达标测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 124.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览


文档简介
2021-2022学年人教版八年级数学下册《17-2勾股定理的逆定理》同步达标测试题(附答案)
一.选择题(共9小题,满分45分)
1.在△ABC中,若AC2﹣BC2=AB2,则( )
A.∠A=90° B.∠B=90° C.∠C=90° D.不能确定
2.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2 B.a:b:c=3:4:5
C.∠C=∠A﹣∠B D.∠A:∠B:∠C=9:12:15
3.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.2,3,4 C.,3,4 D.1,,3
4.一个长方形抽屉长3cm,宽4cm,贴抽屉底面放一根木棒,那么这根木棒最长(不计木棒粗细)可以是( )
A.4cm B.5cm C.6cm D.7cm
5.下列五组数:①4、5、6;②0.6、0.8、1;③7、4、25;④8、15、17;⑤9、40、41,其中是勾股数的组数为( )
A.2 B.3 C.4 D.5
6.已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
7.△ABC中,已知AB=1,AC=2.要使∠B是直角,BC的长度是( )
A. B. C.3 D.或
8.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要( )
A.17m B.18m C.25m D.26m
9.一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口1.5小时后,则两船相距( )
A.10海里 B.20海里 C.30海里 D.40海里
二.填空题(共9小题,满分45分)
10.勾股数为一组连续自然数的是 .
11.已知△ABC中,AB=k,AC=k﹣1,BC=3,当k= 时,∠C=90°.
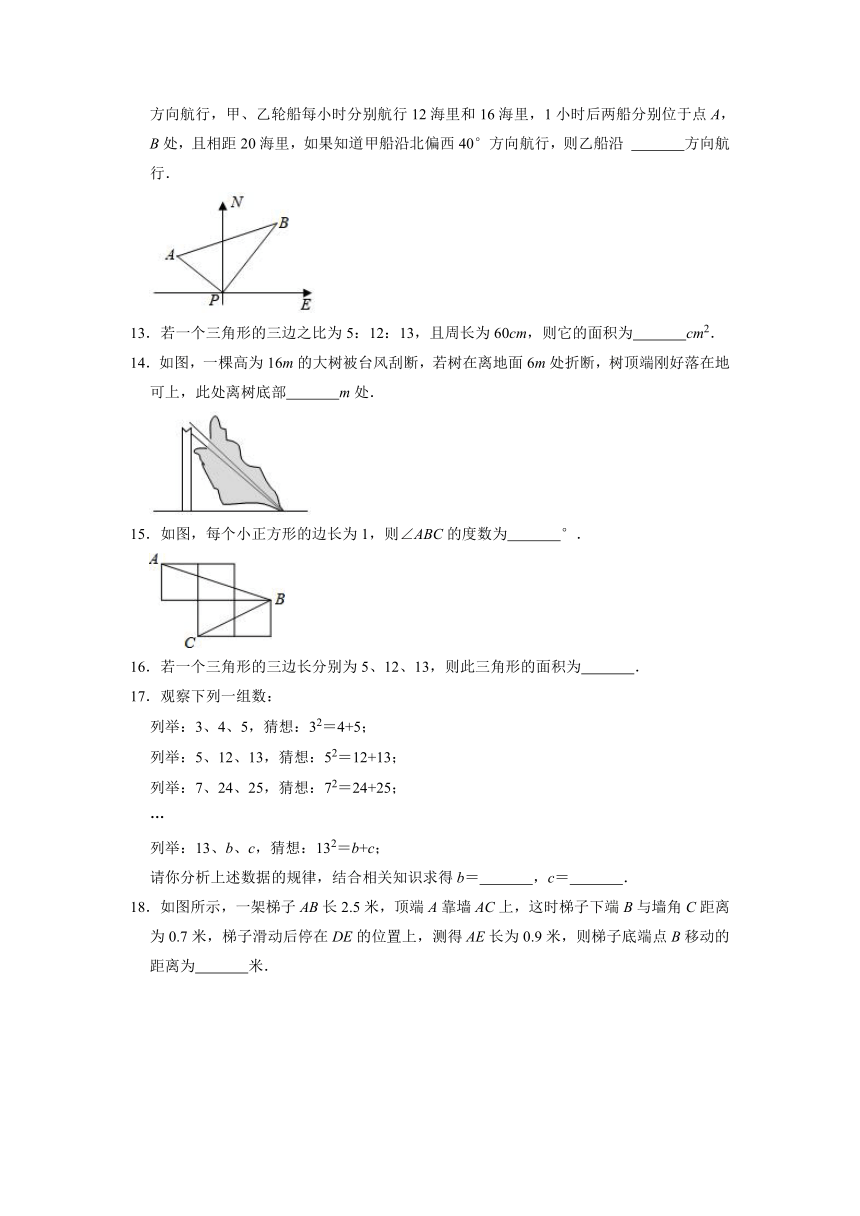
12.如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西40°方向航行,则乙船沿 方向航行.
13.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 cm2.
14.如图,一棵高为16m的大树被台风刮断,若树在离地面6m处折断,树顶端刚好落在地可上,此处离树底部 m处.
15.如图,每个小正方形的边长为1,则∠ABC的度数为 °.
16.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
17.观察下列一组数:
列举:3、4、5,猜想:32=4+5;
列举:5、12、13,猜想:52=12+13;
列举:7、24、25,猜想:72=24+25;
…
列举:13、b、c,猜想:132=b+c;
请你分析上述数据的规律,结合相关知识求得b= ,c= .
18.如图所示,一架梯子AB长2.5米,顶端A靠墙AC上,这时梯子下端B与墙角C距离为0.7米,梯子滑动后停在DE的位置上,测得AE长为0.9米,则梯子底端点B移动的距离为 米.
三.解答题(共4小题,满分30分)
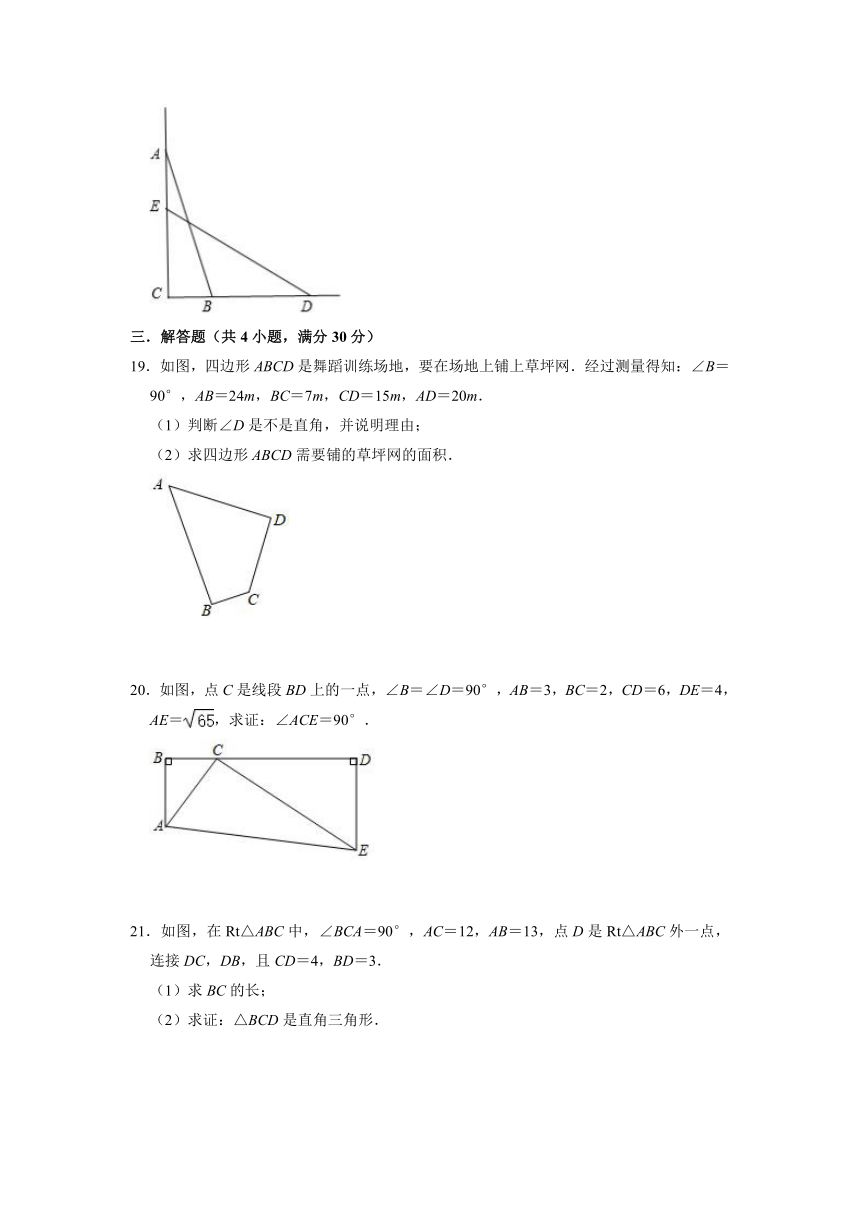
19.如图,四边形ABCD是舞蹈训练场地,要在场地上铺上草坪网.经过测量得知:∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠D是不是直角,并说明理由;
(2)求四边形ABCD需要铺的草坪网的面积.
20.如图,点C是线段BD上的一点,∠B=∠D=90°,AB=3,BC=2,CD=6,DE=4,AE=,求证:∠ACE=90°.
21.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.
(1)求BC的长;
(2)求证:△BCD是直角三角形.
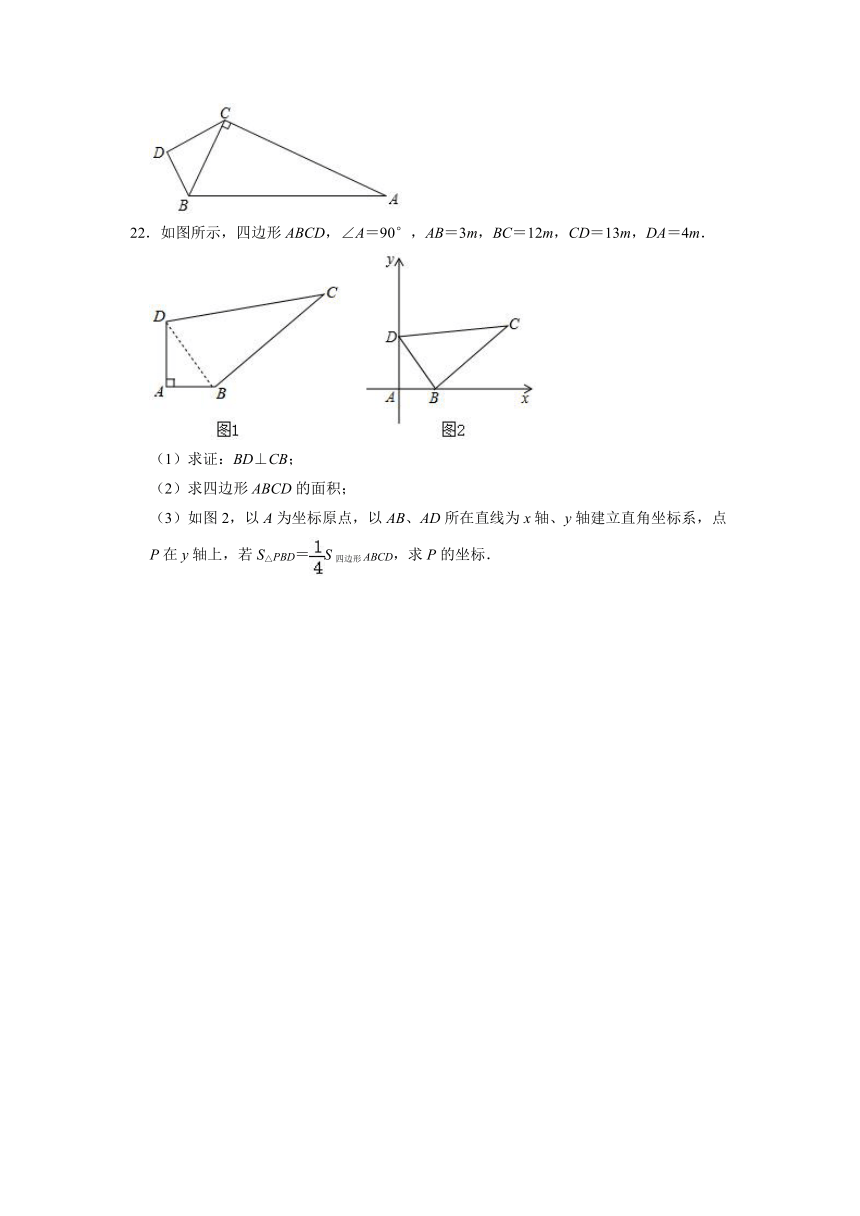
22.如图所示,四边形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形ABCD的面积;
(3)如图2,以A为坐标原点,以AB、AD所在直线为x轴、y轴建立直角坐标系,点P在y轴上,若S△PBD=S四边形ABCD,求P的坐标.
参考答案
一.选择题(共9小题,满分45分)
1.解:∵AC2﹣BC2=AB2,
∴AC2=BC2+AB2,
∴∠B=90°.
故选:B.
2.解:b2﹣c2=a2
则b2=a2+c2
△ABC是直角三角形;
a:b:c=3:4:5,
设a=3x,b=4x,c=5x,
a2+b2=c2,
△ABC是直角三角形;
∠C=∠A﹣∠B,
则∠B=∠A+∠C,
∠B=90°,
△ABC是直角三角形;
∠A:∠B:∠C=9:12:15,
设∠A、∠B、∠C分别为9x、12x、15x,
则9x+12x+15x=180°,
解得,x=5°,
则∠A、∠B、∠C分别为45°,60°,75°,
△ABC不是直角三角形;
故选:D.
3.解:A、42+52≠62,不能构成直角三角形,故不符合题意;
B、22+32≠42,不能构成直角三角形,故不符合题意;
C、()2+32=42,能构成直角三角形,故符合题意;
D、12+()2≠32,不能构成直角三角形,故不符合题意.
故选:C.
4.解:这根木棒最长==5(cm),
故选:B.
5.解:①42+52≠62,故不是勾股数;
②0.6、0.8、1不都是正整数,故不是勾股数;
③72+42≠252,故不是勾股数;
④82+152=172,故是勾股数;
⑤92+402=412,故是勾股数;
其中勾股数有2组,
故选:A.
6.解:∵(a﹣b)(a2+b2﹣c2)=0,
∴a﹣b=0,或a2+b2﹣c2=0,
即a=b或a2+b2=c2,
∴△ABC的形状为等腰三角形或直角三角形.
故选:D.
7.解:∵∠B是直角,故AC为△ABC的斜边,AB为直角边,
∴BC===.
故选:A.
8.解:由勾股定理得:
楼梯的水平宽度==12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是12+5=17(米).
故选:A.
9.解:如图所示:∠1=∠2=45°,AB=12×1.5=18(海里),AC=16×1.5=24(海里),
∴∠BAC=∠1+∠2=90°,即△ABC是直角三角形,
∴BC===30(海里).
故选:C.
二.填空题(共9小题,满分45分)
10.解:设中间的数是x,那么前面的一个就x﹣1,后面的一个就是x+1,根据题意
(x﹣1)2+x2=(x+1)2,
解得:x=0(舍去)或x=4;
4﹣1=3,4+1=5;
故答案为:3、4、5.
11.解:∵∠C=90°,
∴AC2+BC2=AB2,
∵AB=k,AC=k﹣1,BC=3,
∴(k﹣1)2+32=k2,
解得:k=5,
故答案为:5.
12.解:由题意可知:AP=12,BP=16,AB=20,
∵122+162=202,
∴△APB是直角三角形,
∴∠APB=90°,
由题意知∠APN=40°,
∴∠BPN=90°﹣∠APN=90°﹣40°=50°,
即乙船沿北偏东50°方向航行,
故答案为:北偏东50°.
13.解:设三边分别为5x,12x,13x,
则5x+12x+13x=60,
∴x=2,
∴三边分别为10cm,24cm,26cm,
∵102+242=262,
∴三角形为直角三角形,
∴S=10×24÷2=120cm2.
故答案为:120.
14.解:设树顶端落在离树底部x米处,由题意得:
62+x2=(16﹣6)2,
解得:x1=8,x2=﹣8(不合题意舍去).
故答案为:8.
15.解:连接AC,
由勾股定理得:AC2=22+12=5,
BC2=22+12=5,
AB2=12+32=10,
∴AC2+BC2=5+5=10=BA2,
∴△ABC是等腰直角三角形,∠ACB=90°,
∴∠ABC=45°,
故答案为:45.
16.解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为×5×12=30.
17.解:在32=4+5中,4=,5=;
在52=12+13中,12=,13=;
…
则在13、b、c中,b==84,c==85.
18.解:在直角△ABC中,已知AB=2.5米,BC=0.7米,
∴AC===2.4米,
在直角△CDE中,已知DE=AB=2.5米,AE=0.9米,
∴CE=AC﹣AE=1.5米,
∴CD===2米,
∴BD=2米﹣0.7米=1.3米
故答案为:1.3.
三.解答题(共4小题,满分30分)
19.解:连接AC,如图,
,
在Rt△ABC中,AB=24 m,BC=7 m,
∴AC==25 m,
在△ADC中,CD=15 m,AD=20 m.AC=25 m,
∵CD2+AD2=152+202=252=AC2,
∴△ADC为直角三角形,∠D=90°.
(2)由(1)知△ADC为直角三角形,∠D=90°,
∴S△ADC==150 m ,
∵S△ABC= m ,
∴S四边形ABCD=S△ADC+S△ABC=150+84=234 m .
20.证明:在Rt△ABC中,∠B=90°,AB=3,BC=2,
∴AC===.
在Rt△EDC中,∠D=90°,CD=6,DE=4,
∴CE===2,
∵AC2=13,CE2=52,AE2=65,
∴AE2=AC2+CE2,
∴△ACE是直角三角形,AE是斜边,
∴∠ACE=90°.
21.(1)解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC===5;
(2)证明:∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=42+32=52=BC2,
∴△BCD是直角三角形.
22.(1)证明:连接BD.
∵AD=4m,AB=3m,∠BAD=90°,
∴BD=5m.
又∵BC=12m,CD=13m,
∴BD2+BC2=CD2.
∴BD⊥CB;
(2)四边形ABCD的面积=△ABD的面积+△BCD的面积
=×3×4+×12×5
=6+30
=36(m2).
故这块土地的面积是36m2;
(3)∵S△PBD=S四边形ABCD,
∴ PD AB=×36,
∴ PD×3=9,
∴PD=6,
∵D(0,4),点P在y轴上,
∴P的坐标为(0,﹣2)或(0,10).
一.选择题(共9小题,满分45分)
1.在△ABC中,若AC2﹣BC2=AB2,则( )
A.∠A=90° B.∠B=90° C.∠C=90° D.不能确定
2.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2 B.a:b:c=3:4:5
C.∠C=∠A﹣∠B D.∠A:∠B:∠C=9:12:15
3.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.2,3,4 C.,3,4 D.1,,3
4.一个长方形抽屉长3cm,宽4cm,贴抽屉底面放一根木棒,那么这根木棒最长(不计木棒粗细)可以是( )
A.4cm B.5cm C.6cm D.7cm
5.下列五组数:①4、5、6;②0.6、0.8、1;③7、4、25;④8、15、17;⑤9、40、41,其中是勾股数的组数为( )
A.2 B.3 C.4 D.5
6.已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
7.△ABC中,已知AB=1,AC=2.要使∠B是直角,BC的长度是( )
A. B. C.3 D.或
8.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要( )
A.17m B.18m C.25m D.26m
9.一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口1.5小时后,则两船相距( )
A.10海里 B.20海里 C.30海里 D.40海里
二.填空题(共9小题,满分45分)
10.勾股数为一组连续自然数的是 .
11.已知△ABC中,AB=k,AC=k﹣1,BC=3,当k= 时,∠C=90°.
12.如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西40°方向航行,则乙船沿 方向航行.
13.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 cm2.
14.如图,一棵高为16m的大树被台风刮断,若树在离地面6m处折断,树顶端刚好落在地可上,此处离树底部 m处.
15.如图,每个小正方形的边长为1,则∠ABC的度数为 °.
16.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
17.观察下列一组数:
列举:3、4、5,猜想:32=4+5;
列举:5、12、13,猜想:52=12+13;
列举:7、24、25,猜想:72=24+25;
…
列举:13、b、c,猜想:132=b+c;
请你分析上述数据的规律,结合相关知识求得b= ,c= .
18.如图所示,一架梯子AB长2.5米,顶端A靠墙AC上,这时梯子下端B与墙角C距离为0.7米,梯子滑动后停在DE的位置上,测得AE长为0.9米,则梯子底端点B移动的距离为 米.
三.解答题(共4小题,满分30分)
19.如图,四边形ABCD是舞蹈训练场地,要在场地上铺上草坪网.经过测量得知:∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠D是不是直角,并说明理由;
(2)求四边形ABCD需要铺的草坪网的面积.
20.如图,点C是线段BD上的一点,∠B=∠D=90°,AB=3,BC=2,CD=6,DE=4,AE=,求证:∠ACE=90°.
21.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.
(1)求BC的长;
(2)求证:△BCD是直角三角形.
22.如图所示,四边形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形ABCD的面积;
(3)如图2,以A为坐标原点,以AB、AD所在直线为x轴、y轴建立直角坐标系,点P在y轴上,若S△PBD=S四边形ABCD,求P的坐标.
参考答案
一.选择题(共9小题,满分45分)
1.解:∵AC2﹣BC2=AB2,
∴AC2=BC2+AB2,
∴∠B=90°.
故选:B.
2.解:b2﹣c2=a2
则b2=a2+c2
△ABC是直角三角形;
a:b:c=3:4:5,
设a=3x,b=4x,c=5x,
a2+b2=c2,
△ABC是直角三角形;
∠C=∠A﹣∠B,
则∠B=∠A+∠C,
∠B=90°,
△ABC是直角三角形;
∠A:∠B:∠C=9:12:15,
设∠A、∠B、∠C分别为9x、12x、15x,
则9x+12x+15x=180°,
解得,x=5°,
则∠A、∠B、∠C分别为45°,60°,75°,
△ABC不是直角三角形;
故选:D.
3.解:A、42+52≠62,不能构成直角三角形,故不符合题意;
B、22+32≠42,不能构成直角三角形,故不符合题意;
C、()2+32=42,能构成直角三角形,故符合题意;
D、12+()2≠32,不能构成直角三角形,故不符合题意.
故选:C.
4.解:这根木棒最长==5(cm),
故选:B.
5.解:①42+52≠62,故不是勾股数;
②0.6、0.8、1不都是正整数,故不是勾股数;
③72+42≠252,故不是勾股数;
④82+152=172,故是勾股数;
⑤92+402=412,故是勾股数;
其中勾股数有2组,
故选:A.
6.解:∵(a﹣b)(a2+b2﹣c2)=0,
∴a﹣b=0,或a2+b2﹣c2=0,
即a=b或a2+b2=c2,
∴△ABC的形状为等腰三角形或直角三角形.
故选:D.
7.解:∵∠B是直角,故AC为△ABC的斜边,AB为直角边,
∴BC===.
故选:A.
8.解:由勾股定理得:
楼梯的水平宽度==12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是12+5=17(米).
故选:A.
9.解:如图所示:∠1=∠2=45°,AB=12×1.5=18(海里),AC=16×1.5=24(海里),
∴∠BAC=∠1+∠2=90°,即△ABC是直角三角形,
∴BC===30(海里).
故选:C.
二.填空题(共9小题,满分45分)
10.解:设中间的数是x,那么前面的一个就x﹣1,后面的一个就是x+1,根据题意
(x﹣1)2+x2=(x+1)2,
解得:x=0(舍去)或x=4;
4﹣1=3,4+1=5;
故答案为:3、4、5.
11.解:∵∠C=90°,
∴AC2+BC2=AB2,
∵AB=k,AC=k﹣1,BC=3,
∴(k﹣1)2+32=k2,
解得:k=5,
故答案为:5.
12.解:由题意可知:AP=12,BP=16,AB=20,
∵122+162=202,
∴△APB是直角三角形,
∴∠APB=90°,
由题意知∠APN=40°,
∴∠BPN=90°﹣∠APN=90°﹣40°=50°,
即乙船沿北偏东50°方向航行,
故答案为:北偏东50°.
13.解:设三边分别为5x,12x,13x,
则5x+12x+13x=60,
∴x=2,
∴三边分别为10cm,24cm,26cm,
∵102+242=262,
∴三角形为直角三角形,
∴S=10×24÷2=120cm2.
故答案为:120.
14.解:设树顶端落在离树底部x米处,由题意得:
62+x2=(16﹣6)2,
解得:x1=8,x2=﹣8(不合题意舍去).
故答案为:8.
15.解:连接AC,
由勾股定理得:AC2=22+12=5,
BC2=22+12=5,
AB2=12+32=10,
∴AC2+BC2=5+5=10=BA2,
∴△ABC是等腰直角三角形,∠ACB=90°,
∴∠ABC=45°,
故答案为:45.
16.解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为×5×12=30.
17.解:在32=4+5中,4=,5=;
在52=12+13中,12=,13=;
…
则在13、b、c中,b==84,c==85.
18.解:在直角△ABC中,已知AB=2.5米,BC=0.7米,
∴AC===2.4米,
在直角△CDE中,已知DE=AB=2.5米,AE=0.9米,
∴CE=AC﹣AE=1.5米,
∴CD===2米,
∴BD=2米﹣0.7米=1.3米
故答案为:1.3.
三.解答题(共4小题,满分30分)
19.解:连接AC,如图,
,
在Rt△ABC中,AB=24 m,BC=7 m,
∴AC==25 m,
在△ADC中,CD=15 m,AD=20 m.AC=25 m,
∵CD2+AD2=152+202=252=AC2,
∴△ADC为直角三角形,∠D=90°.
(2)由(1)知△ADC为直角三角形,∠D=90°,
∴S△ADC==150 m ,
∵S△ABC= m ,
∴S四边形ABCD=S△ADC+S△ABC=150+84=234 m .
20.证明:在Rt△ABC中,∠B=90°,AB=3,BC=2,
∴AC===.
在Rt△EDC中,∠D=90°,CD=6,DE=4,
∴CE===2,
∵AC2=13,CE2=52,AE2=65,
∴AE2=AC2+CE2,
∴△ACE是直角三角形,AE是斜边,
∴∠ACE=90°.
21.(1)解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC===5;
(2)证明:∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=42+32=52=BC2,
∴△BCD是直角三角形.
22.(1)证明:连接BD.
∵AD=4m,AB=3m,∠BAD=90°,
∴BD=5m.
又∵BC=12m,CD=13m,
∴BD2+BC2=CD2.
∴BD⊥CB;
(2)四边形ABCD的面积=△ABD的面积+△BCD的面积
=×3×4+×12×5
=6+30
=36(m2).
故这块土地的面积是36m2;
(3)∵S△PBD=S四边形ABCD,
∴ PD AB=×36,
∴ PD×3=9,
∴PD=6,
∵D(0,4),点P在y轴上,
∴P的坐标为(0,﹣2)或(0,10).
