2021-2022学年鲁教版(五四制)八年级数学下册6.1菱形的性质与判定同步达标测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.1菱形的性质与判定同步达标测试(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 249.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 14:36:57 | ||
图片预览




文档简介
2021-2022学年鲁教版八年级数学下册《6-1菱形的性质与判定》同步达标测试(附答案)
一.选择题(共10小题,满分40分)
1.如图,菱形ABCD的两条对角线相交于点O,若AC=6,菱形的面积等于12,则菱形ABCD的周长等于( )
A.4 B.2 C. D.4
2.已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为( )
A.4 B.2 C.2 D.1
3.平行四边形ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC⊥BD B.∠ABD=∠CBD C.AB=BC D.AC=BD
4.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为( )
A. B. C. D.5
5.菱形的边长为5,一条对角线长为8,则此菱形的面积是( )
A.24 B.30 C.40 D.48
6.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )
A.12 B.16 C.20 D.24
7.如图,菱形ABCD的顶点C在直线MN上,若∠1=50°,∠2=20°,则∠BDC的度数为( )
A.20° B.30° C.35° D.40°
8.如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连接OE.若OB=6,菱形ABCD的面积为54,则OE的长为( )
A.4 B.4.5 C.8 D.9
9.如图,菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE,若∠ABC=140°,则∠OED=( )
A.20° B.30° C.40° D.50°
10.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
A.3 B.3 C.2 D.4
二.填空题(共5小题,满分25分)
11.菱形ABCD的边长为6,∠ABC=60°,则较长对角线BD的长是 .
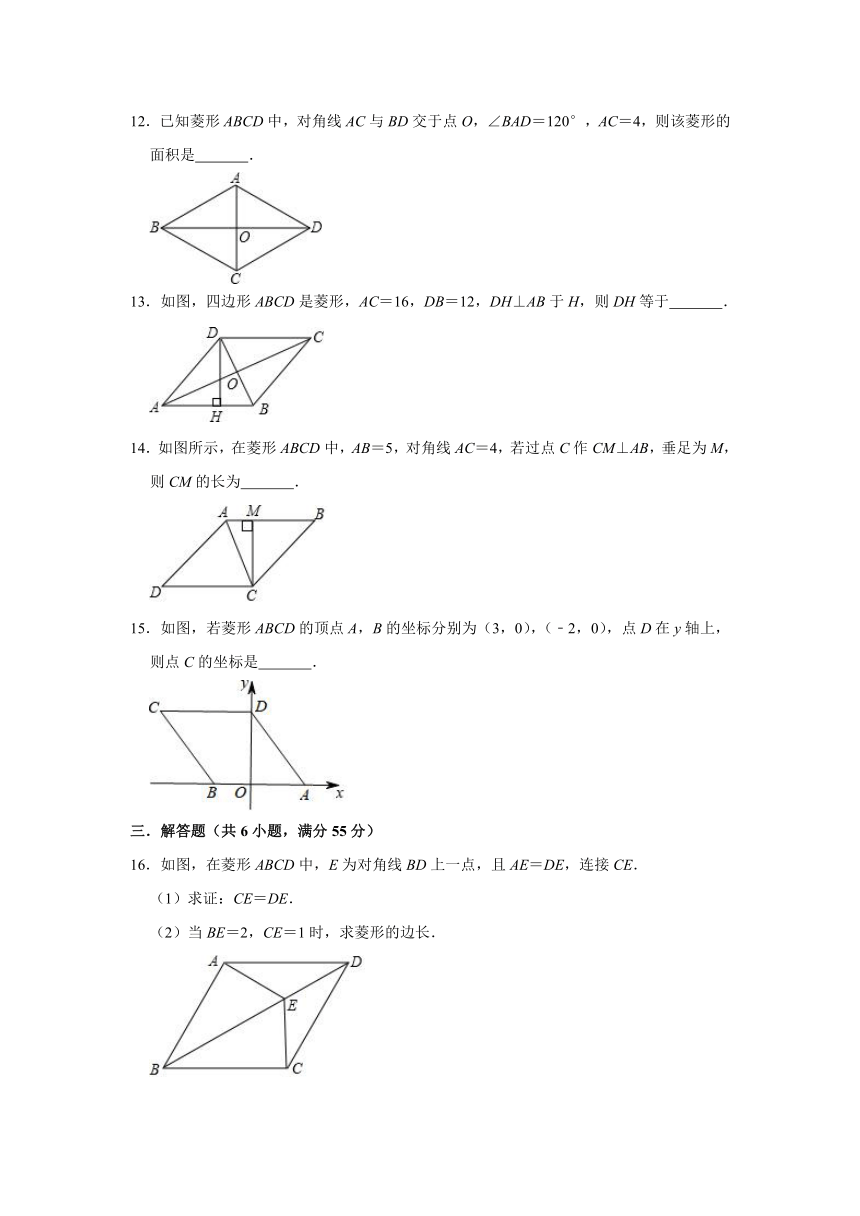
12.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是 .
13.如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于H,则DH等于 .
14.如图所示,在菱形ABCD中,AB=5,对角线AC=4,若过点C作CM⊥AB,垂足为M,则CM的长为 .
15.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是 .
三.解答题(共6小题,满分55分)
16.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
17.如图,在 ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证: ABCD是菱形;
(2)若AB=5,AC=6,求 ABCD的面积.
18.如图,已知点E,F分别是 ABCD的边BC,AD上的中点,且∠BAC=90°.
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
19.如图,在平行四边形ABCD中,按下列步骤作图:
①以点B为圆心,以适当长为半径作弧,交AB于点N.交BC于点M;
②再分别以点M和点N为圆心,大于MN的长为半径作弧,两弧交于点G;
③作射线BG交AD于F;
④过点A作AE⊥BF交BF于点P,交BC于点E;
⑤连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=8,AD=10,∠ABC=60°,求DP的长.
20.在 ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点O,连接EF、OC.
(1)求证:四边形ABEF是菱形;
(2)若点E为BC的中点,且BC=8,∠ABC=60°,求OC的长.
21.已知:如图,在 ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,过点F作FG⊥BF交BC的延长线于点G.
(1)求证:四边形ABEF是菱形;
(2)如果AB=2,∠BAD=60°,求FG的长.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵菱形的面积等于12,
∴AC BD=12,
∵AC=6,
∴BD=4,
∵菱形ABCD对角线互相垂直平分,
∴BO=OD=2,AO=OC=3,
∴AB===,
∴菱形的周长为4.
故选:D.
2.解:如图,∵四边形ABCD是菱形,周长为8,
∴AB=BC=CD=AD=2,AD∥BC,
∴∠B+∠BAD=180°,
∴∠B=180°﹣120°=60°,
∴△ABC为等边三角形,
∴AC=AB=2,
即该菱形较短的对角线长为2,
故选:C.
3.解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
又∵∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC,
∴平行四边形ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故选项D不符合题意;
故选:D.
4.解:过点A作AE⊥CD于E,AF⊥BC于F,连接AC,BD交于点O,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S ABCD=BC AF=CD AE.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
∴AO=CO=1,BO=DO,AC⊥BD,
∴BO===2,
∴BD=4,
∴四边形ABCD的面积==4,
故选:A.
5.解:在菱形ABCD中,AB=5,BD=8,
∵对角线互相垂直平分,
∴∠AOB=90°,BO=4,
在RT△AOB中,AO==3,
∴AC=2AO=6.
∴则此菱形面积是:=24.
故选:A.
6.解:∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴BC=2EF=2×3=6,
∴菱形ABCD的周长=4BC=4×6=24.
故选:D.
7.解:∵∠1=50°,∠2=20°,
∴∠BCD=110°,
在菱形ABCD中,
BC=CD,
∴∠BDC=35°,
故选:C.
8.解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD=BD,BD⊥AC,
∴BD=2OB=12,
∵S菱形ABCD=AC×BD=54,
∴AC=9,
∵AE⊥BC,
∴∠AEC=90°,
∴OE=AC=4.5,
故选:B.
9.解:∵四边形ABCD是菱形,
∴O为BD中点,∠DBE=∠ABC=70°.
∵DE⊥BC,
∴在Rt△BDE中,OE=OB=OD,
∴∠OEB=∠OBE=70°.
∴∠OED=90°﹣70°=20°.
故选:A.
10.解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∵四边形ABCD是菱形,
∴BD⊥AC于O,AO=AC=×6=3,
由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=3.
故选:A.
二.填空题(共5小题,满分25分)
11.解:∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC=CD=AD=6,∠ABC=∠ADC=60°,AC⊥BD,OA=OC,OB=OD,
∴△ABC,△ADC是等边三角形,
∴AC=6,OD=OC=3,
在Rt△AOB中,BO==3,
∴BD=2OB=6,
故答案为6.
12.解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=×4=2,∠BAC=∠BAD=×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB=2,
∴BD=2OB=4,
∴该菱形的面积是:AC BD=×4×4=8.
故答案为:8.
13.解:∵四边形ABCD是菱形,
∴OA=OC=8,OB=OD=6,AC⊥BD,
在Rt△AOB中,AB==10,
∵S菱形ABCD= AC BD,
S菱形ABCD=DH AB,
∴DH 10=×12×16,
∴DH=.
故答案为:.
14.解:连接BD交AC于O.
∵四边形ABCD是菱形,
∴AC⊥BD,OC=OA=2,
∵AB=5,
∴OB==,
∴BD=2,
∵S菱形ABCD=×AC×BD=AB×CM,
∴CM=,
故答案为.
15.解:∵菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,
∴AB=5,
∴AD=5,
∴由勾股定理知:OD===4,
∴点C的坐标是:(﹣5,4).
故答案为:(﹣5,4).
三.解答题(共6小题,满分55分)
16.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BH=BD=,EH=BE﹣BH=2﹣=,
在Rt△AHE中,由勾股定理得:AH===,
在Rt△AHB中,由勾股定理得:AB===,
∴菱形的边长为.
17.(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∵BE=DF,
∴△AEB≌△AFD
∴AB=AD,
∴四边形ABCD是菱形.
(2)连接BD交AC于O.
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,
AO=OC=AC=×6=3,
∵AB=5,AO=3,
∴BO===4,
∴BD=2BO=8,
∴S平行四边形ABCD=×AC×BD=24.
18.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,
在Rt△ABC中,∠BAC=90°,点E是BC边的中点,
∴AE=BC=CE,
同理,AF=AD=CF,
∴AE=CE=AF=CF,
∴四边形AECF是菱形;
(2)连接EF交AC于点O,如图所示:
在Rt△ABC中,∠BAC=90°,∠B=30°,BC=10,
∴AC=BC=5,AB=AC=5,
∵四边形AECF是菱形,
∴AC⊥EF,OA=OC,
∴OE是△ABC的中位线,
∴OE=AB=,
∴EF=5,
∴菱形AECF的面积=AC EF=×5×5=.
19.(1)证明:由作图知BA=BE,∠ABF=∠EBF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EBF=∠AFB,
∴∠ABF=∠AFB,
∴AB=AF=BE,
∴四边形ABEF是平行四边形,
又AB=BE,
∴四边形ABEF是菱形;
(2)解:作PH⊥AD于H,
∵四边形ABEF是菱形,∠ABC=60°,AB=8,
∴AB=AF=8,∠ABF=∠AFB=30°,AP⊥BF,
∴AP=AB=4,
∴PH=2,DH=8,
∴DP===2.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AF∥BE,
∴∠AFB=∠FBE,
∵BF平分∠ABC,
∴∠ABF=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
同理AB=BE,
∴AF=BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形;
(2)解:过O作OH⊥BC于H,
∵E为BC的中点,且BC=8,
∴BE=CE=4,
∵四边形ABEF是菱形,∠ABC=60°,
∴∠OBH=30°,∠BOE=90°,
∴OE=BE=2,∠EOH=∠OBH=90°﹣∠OEH=30°,
∴EH=OE=1,
∴OH2=OE2﹣EH2=,
∴CH=EH+CE=5,
∴OC==2.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴∠AEB=∠BAE.
∴AB=BE.
同理:AB=AF.
∴AF=BE,AF∥BE,
∴四边形ABEF是平行四边形,
又∵AB=BE,
∴四边形ABEF是菱形;
(2)解:∵四边形ABEF是菱形,
∴AE⊥BF,OA=OE,OB=OF,AE平分∠BAD
∵AB=2,∠BAD=60°,
∴∠BAE=30°
∴OB=OF=1,OA=OE=,
∴OE∥FG,
∴,
∴FG=2.
一.选择题(共10小题,满分40分)
1.如图,菱形ABCD的两条对角线相交于点O,若AC=6,菱形的面积等于12,则菱形ABCD的周长等于( )
A.4 B.2 C. D.4
2.已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为( )
A.4 B.2 C.2 D.1
3.平行四边形ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC⊥BD B.∠ABD=∠CBD C.AB=BC D.AC=BD
4.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为( )
A. B. C. D.5
5.菱形的边长为5,一条对角线长为8,则此菱形的面积是( )
A.24 B.30 C.40 D.48
6.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )
A.12 B.16 C.20 D.24
7.如图,菱形ABCD的顶点C在直线MN上,若∠1=50°,∠2=20°,则∠BDC的度数为( )
A.20° B.30° C.35° D.40°
8.如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连接OE.若OB=6,菱形ABCD的面积为54,则OE的长为( )
A.4 B.4.5 C.8 D.9
9.如图,菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE,若∠ABC=140°,则∠OED=( )
A.20° B.30° C.40° D.50°
10.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
A.3 B.3 C.2 D.4
二.填空题(共5小题,满分25分)
11.菱形ABCD的边长为6,∠ABC=60°,则较长对角线BD的长是 .
12.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是 .
13.如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于H,则DH等于 .
14.如图所示,在菱形ABCD中,AB=5,对角线AC=4,若过点C作CM⊥AB,垂足为M,则CM的长为 .
15.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是 .
三.解答题(共6小题,满分55分)
16.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
17.如图,在 ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证: ABCD是菱形;
(2)若AB=5,AC=6,求 ABCD的面积.
18.如图,已知点E,F分别是 ABCD的边BC,AD上的中点,且∠BAC=90°.
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
19.如图,在平行四边形ABCD中,按下列步骤作图:
①以点B为圆心,以适当长为半径作弧,交AB于点N.交BC于点M;
②再分别以点M和点N为圆心,大于MN的长为半径作弧,两弧交于点G;
③作射线BG交AD于F;
④过点A作AE⊥BF交BF于点P,交BC于点E;
⑤连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=8,AD=10,∠ABC=60°,求DP的长.
20.在 ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点O,连接EF、OC.
(1)求证:四边形ABEF是菱形;
(2)若点E为BC的中点,且BC=8,∠ABC=60°,求OC的长.
21.已知:如图,在 ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,过点F作FG⊥BF交BC的延长线于点G.
(1)求证:四边形ABEF是菱形;
(2)如果AB=2,∠BAD=60°,求FG的长.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵菱形的面积等于12,
∴AC BD=12,
∵AC=6,
∴BD=4,
∵菱形ABCD对角线互相垂直平分,
∴BO=OD=2,AO=OC=3,
∴AB===,
∴菱形的周长为4.
故选:D.
2.解:如图,∵四边形ABCD是菱形,周长为8,
∴AB=BC=CD=AD=2,AD∥BC,
∴∠B+∠BAD=180°,
∴∠B=180°﹣120°=60°,
∴△ABC为等边三角形,
∴AC=AB=2,
即该菱形较短的对角线长为2,
故选:C.
3.解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
又∵∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC,
∴平行四边形ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故选项D不符合题意;
故选:D.
4.解:过点A作AE⊥CD于E,AF⊥BC于F,连接AC,BD交于点O,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S ABCD=BC AF=CD AE.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
∴AO=CO=1,BO=DO,AC⊥BD,
∴BO===2,
∴BD=4,
∴四边形ABCD的面积==4,
故选:A.
5.解:在菱形ABCD中,AB=5,BD=8,
∵对角线互相垂直平分,
∴∠AOB=90°,BO=4,
在RT△AOB中,AO==3,
∴AC=2AO=6.
∴则此菱形面积是:=24.
故选:A.
6.解:∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴BC=2EF=2×3=6,
∴菱形ABCD的周长=4BC=4×6=24.
故选:D.
7.解:∵∠1=50°,∠2=20°,
∴∠BCD=110°,
在菱形ABCD中,
BC=CD,
∴∠BDC=35°,
故选:C.
8.解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD=BD,BD⊥AC,
∴BD=2OB=12,
∵S菱形ABCD=AC×BD=54,
∴AC=9,
∵AE⊥BC,
∴∠AEC=90°,
∴OE=AC=4.5,
故选:B.
9.解:∵四边形ABCD是菱形,
∴O为BD中点,∠DBE=∠ABC=70°.
∵DE⊥BC,
∴在Rt△BDE中,OE=OB=OD,
∴∠OEB=∠OBE=70°.
∴∠OED=90°﹣70°=20°.
故选:A.
10.解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∵四边形ABCD是菱形,
∴BD⊥AC于O,AO=AC=×6=3,
由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=3.
故选:A.
二.填空题(共5小题,满分25分)
11.解:∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC=CD=AD=6,∠ABC=∠ADC=60°,AC⊥BD,OA=OC,OB=OD,
∴△ABC,△ADC是等边三角形,
∴AC=6,OD=OC=3,
在Rt△AOB中,BO==3,
∴BD=2OB=6,
故答案为6.
12.解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=×4=2,∠BAC=∠BAD=×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB=2,
∴BD=2OB=4,
∴该菱形的面积是:AC BD=×4×4=8.
故答案为:8.
13.解:∵四边形ABCD是菱形,
∴OA=OC=8,OB=OD=6,AC⊥BD,
在Rt△AOB中,AB==10,
∵S菱形ABCD= AC BD,
S菱形ABCD=DH AB,
∴DH 10=×12×16,
∴DH=.
故答案为:.
14.解:连接BD交AC于O.
∵四边形ABCD是菱形,
∴AC⊥BD,OC=OA=2,
∵AB=5,
∴OB==,
∴BD=2,
∵S菱形ABCD=×AC×BD=AB×CM,
∴CM=,
故答案为.
15.解:∵菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,
∴AB=5,
∴AD=5,
∴由勾股定理知:OD===4,
∴点C的坐标是:(﹣5,4).
故答案为:(﹣5,4).
三.解答题(共6小题,满分55分)
16.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BH=BD=,EH=BE﹣BH=2﹣=,
在Rt△AHE中,由勾股定理得:AH===,
在Rt△AHB中,由勾股定理得:AB===,
∴菱形的边长为.
17.(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∵BE=DF,
∴△AEB≌△AFD
∴AB=AD,
∴四边形ABCD是菱形.
(2)连接BD交AC于O.
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,
AO=OC=AC=×6=3,
∵AB=5,AO=3,
∴BO===4,
∴BD=2BO=8,
∴S平行四边形ABCD=×AC×BD=24.
18.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,
在Rt△ABC中,∠BAC=90°,点E是BC边的中点,
∴AE=BC=CE,
同理,AF=AD=CF,
∴AE=CE=AF=CF,
∴四边形AECF是菱形;
(2)连接EF交AC于点O,如图所示:
在Rt△ABC中,∠BAC=90°,∠B=30°,BC=10,
∴AC=BC=5,AB=AC=5,
∵四边形AECF是菱形,
∴AC⊥EF,OA=OC,
∴OE是△ABC的中位线,
∴OE=AB=,
∴EF=5,
∴菱形AECF的面积=AC EF=×5×5=.
19.(1)证明:由作图知BA=BE,∠ABF=∠EBF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EBF=∠AFB,
∴∠ABF=∠AFB,
∴AB=AF=BE,
∴四边形ABEF是平行四边形,
又AB=BE,
∴四边形ABEF是菱形;
(2)解:作PH⊥AD于H,
∵四边形ABEF是菱形,∠ABC=60°,AB=8,
∴AB=AF=8,∠ABF=∠AFB=30°,AP⊥BF,
∴AP=AB=4,
∴PH=2,DH=8,
∴DP===2.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AF∥BE,
∴∠AFB=∠FBE,
∵BF平分∠ABC,
∴∠ABF=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
同理AB=BE,
∴AF=BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形;
(2)解:过O作OH⊥BC于H,
∵E为BC的中点,且BC=8,
∴BE=CE=4,
∵四边形ABEF是菱形,∠ABC=60°,
∴∠OBH=30°,∠BOE=90°,
∴OE=BE=2,∠EOH=∠OBH=90°﹣∠OEH=30°,
∴EH=OE=1,
∴OH2=OE2﹣EH2=,
∴CH=EH+CE=5,
∴OC==2.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴∠AEB=∠BAE.
∴AB=BE.
同理:AB=AF.
∴AF=BE,AF∥BE,
∴四边形ABEF是平行四边形,
又∵AB=BE,
∴四边形ABEF是菱形;
(2)解:∵四边形ABEF是菱形,
∴AE⊥BF,OA=OE,OB=OF,AE平分∠BAD
∵AB=2,∠BAD=60°,
∴∠BAE=30°
∴OB=OF=1,OA=OE=,
∴OE∥FG,
∴,
∴FG=2.
