1.1 简单几何体学案(北师大版必修2)
文档属性
| 名称 | 1.1 简单几何体学案(北师大版必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 285.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-08 09:01:59 | ||
图片预览

文档简介
§1 简单几何体
自主学习
1.能根据圆柱、圆锥、圆台和球的定义及结构特征,掌握它们的相关概念和表示方法.
2.能根据棱柱、棱锥、棱台的定义和结构特征,掌握它们的相关概念、分类和表示方法.
1.以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面叫作________,球面所围成的几何体叫作________,简称______.半圆的圆心叫作________.
用一个平面去截一个球,截面是圆面.球面被经过球心的平面截得的圆叫作大圆.
2.分别以矩形的一边、直角三角形的一条直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫作________________________.
3.在旋转轴上这条边的长度叫作它们的高,垂直于旋转轴的边旋转而成的圆面叫作它们的________,不垂直于旋转轴的边旋转而成的曲面叫作它们的________,无论转到什么位置,这条边都叫作侧面的________.
4.棱柱的结构特征:两个面____________,其余各面都是__________,并且每相邻两个四边形的公共边都________________,由这些面围成的几何体叫做棱柱.侧棱垂直于底面的棱柱叫作____________,底面是正多边形的直棱柱叫作__________.
5.棱锥的结构特征:有一个面是__________,其余各面是
________________________________,这些面围成的几何体叫棱锥.如果棱锥的底面是____________,且各侧面________,就称作正棱锥.
6.棱台的结构特征:用一个__________棱锥底面的平面去截棱锥,________________
之间的部分叫作棱台.
对点讲练
旋转体的有关概念
例1 有以下命题:
①以直角三角形一边为旋转轴,旋转所得的旋转体是圆锥;②以直角梯形的一条腰所在直线为旋转轴,旋转所得的几何体是圆台;③圆柱、圆锥、圆台的底面都是圆;④分别以矩形两条不同的边所在直线为旋转轴,将矩形旋转,所得的两个圆柱可能是两个不同的圆柱.
其中正确的个数有( )
A.1 B.2 C.3 D.4
点评 本题是考查圆柱、圆锥、圆台概念的理解问题.对几何体的概念理解要到位,稍有疏忽都会造成错误的判断,做题时要注意哪条边所在直线为旋转轴,必须清楚地认识到:以直角三角形的一条直角边所在直线为旋转轴旋转得圆锥,以斜边为旋转轴旋转就是两个圆锥的组合体;以直角梯形垂直于底的腰所在直线为旋转轴旋转得圆台,以斜腰所在直线为旋转轴把直角梯形旋转一周得两个圆锥和一个圆台的组合体.
变式训练1 下列命题中,错误的是( )
A.圆柱的轴截面是过母线的截面中面积最大的一个
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.圆台的所有平行于底面的截面都是圆面
D.圆锥所有的轴截面是全等的等腰三角形
多面体的有关概念
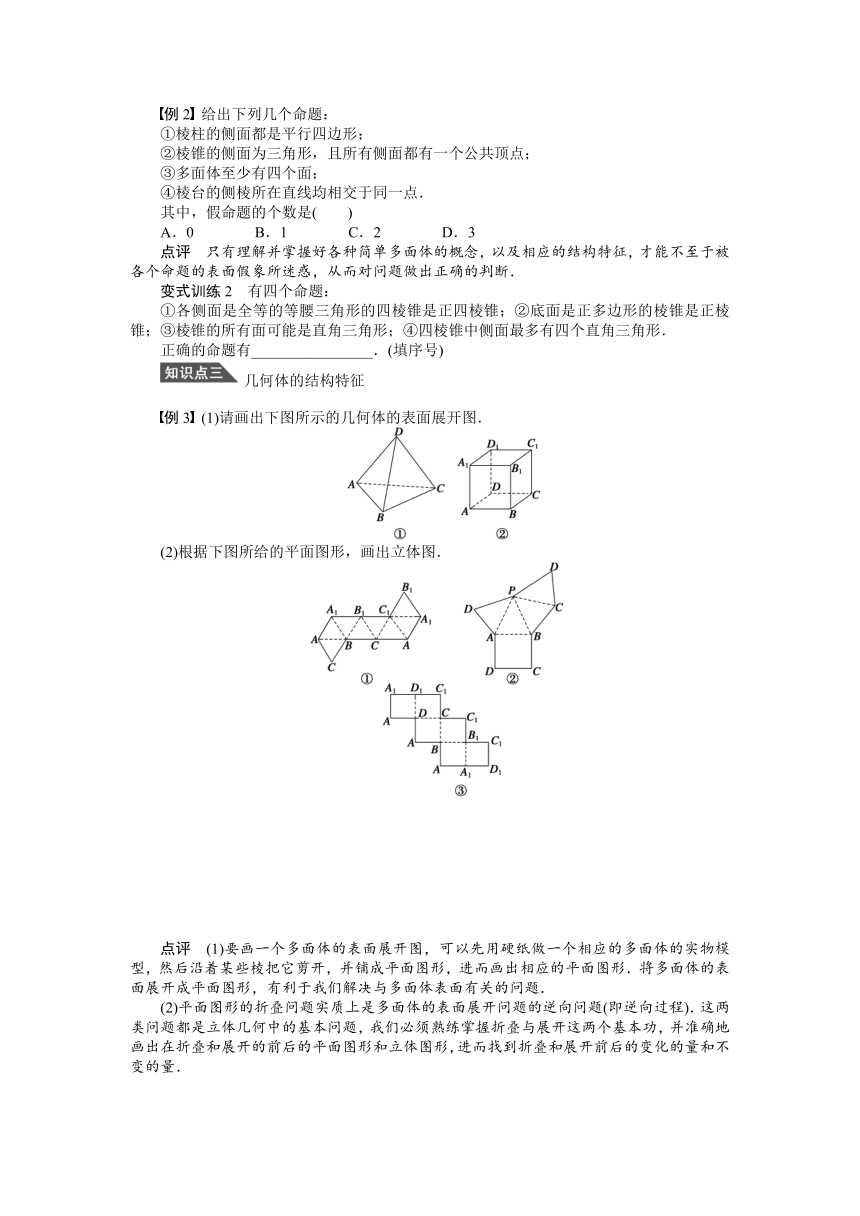
例2 给出下列几个命题:
①棱柱的侧面都是平行四边形;
②棱锥的侧面为三角形,且所有侧面都有一个公共顶点;
③多面体至少有四个面;
④棱台的侧棱所在直线均相交于同一点.
其中,假命题的个数是( )
A.0 B.1 C.2 D.3
点评 只有理解并掌握好各种简单多面体的概念,以及相应的结构特征,才能不至于被各个命题的表面假象所迷惑,从而对问题做出正确的判断.
变式训练2 有四个命题:
①各侧面是全等的等腰三角形的四棱锥是正四棱锥;②底面是正多边形的棱锥是正棱锥;③棱锥的所有面可能是直角三角形;④四棱锥中侧面最多有四个直角三角形.
正确的命题有________________.(填序号)
几何体的结构特征
例3 (1)请画出下图所示的几何体的表面展开图.
(2)根据下图所给的平面图形,画出立体图.
点评 (1)要画一个多面体的表面展开图,可以先用硬纸做一个相应的多面体的实物模型,然后沿着某些棱把它剪开,并铺成平面图形,进而画出相应的平面图形.将多面体的表面展开成平面图形,有利于我们解决与多面体表面有关的问题.
(2)平面图形的折叠问题实质上是多面体的表面展开问题的逆向问题(即逆向过程).这两类问题都是立体几何中的基本问题,我们必须熟练掌握折叠与展开这两个基本功,并准确地画出在折叠和展开的前后的平面图形和立体图形,进而找到折叠和展开前后的变化的量和不变的量.
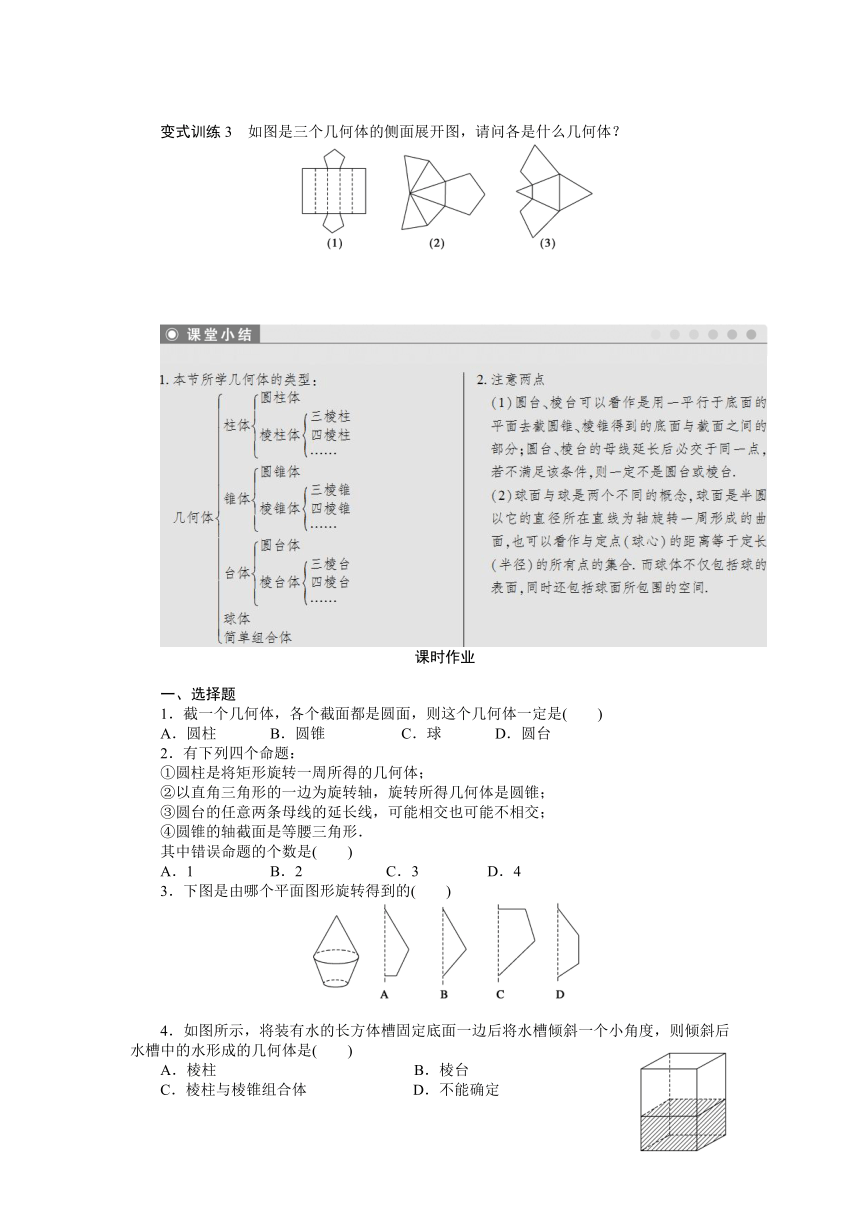
变式训练3 如图是三个几何体的侧面展开图,请问各是什么几何体?
课时作业
一、选择题
1.截一个几何体,各个截面都是圆面,则这个几何体一定是( )
A.圆柱 B.圆锥 C.球 D.圆台
2.有下列四个命题:
①圆柱是将矩形旋转一周所得的几何体;
②以直角三角形的一边为旋转轴,旋转所得几何体是圆锥;
③圆台的任意两条母线的延长线,可能相交也可能不相交;
④圆锥的轴截面是等腰三角形.
其中错误命题的个数是( )
A.1 B.2 C.3 D.4
3.下图是由哪个平面图形旋转得到的( )
4.如图所示,将装有水的长方体槽固定底面一边后将水槽倾斜一个小角度,则倾斜后水槽中的水形成的几何体是( )
A.棱柱 B.棱台
C.棱柱与棱锥组合体 D.不能确定
5.下图中不可能围成正方体的是( )
二、填空题
6.在下面4个平面图形中,哪几个是下面各侧棱都相等的四面体的展开图?其序号是______.(把你认为正确的序号都填上)
7.下列命题中:①用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫棱台;②棱台的各侧棱延长后一定相交于一点;③圆台可以看作直角梯形绕与底边垂直的腰所在直线旋转而成的几何体;④半圆绕其直径所在直线旋转一周形成球.正确命题的序号为__________.
三、解答题
8.如图所示为长方体ABCD—A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由.
9.四边形ABCD为直角梯形,分别以边AD、边AB、边CD所在直线为轴旋转,分析所形成的三个几何体的结构特征.
第一章 立体几何
§1 简单几何体
答案
自学导引
1.球面 球体 球 球心
2.圆柱、圆锥、圆台
3.底面 侧面 母线
4.互相平行 四边形 互相平行 直棱柱 正棱柱
5.多边形 有一个公共顶点的三角形 正多边形 全等
6.平行于 底面与截面
对点讲练
例1 A [圆锥是以直角三角形的一条直角边所在直线为旋转轴的,如果以斜边所在直线为旋转轴旋转,那就变成一个组合体了,故①错误;圆台是以直角梯形与底边垂直的腰所在直线为旋转轴的,故②错误;圆柱、圆锥、圆台的底面为圆面,③错误;根据圆柱的定义可知,无论以矩形的哪条边所在直线为旋转轴,旋转所得的曲面围成的几何体都是圆柱,但它们并不一定是相同的圆柱,故④正确,因此正确的命题有1个.]
变式训练1 B
例2 A [显然命题①、②均是真命题.
对于命题③,显然一个图形要成为空间几何体,它至少需有四个顶点,因为三个顶点只围成一个平面图形是三角形,当有四个顶点时,易知它可围成四个面,因而一个多面体至少应有四个面,而且这样的面必是三角形,故命题③是真命题.
对于命题④,棱台的侧棱所在的直线就是截得原棱锥的侧棱所在的直线,而棱锥的侧棱都有一个公共的点,它便是棱锥的顶点,于是棱台的侧棱所在的直线均相交于同一点,故命题④为真命题.]
变式训练2 ③④
例3 解 (1)将立体图形沿着某些棱剪开,然后伸展到平面上.展开图如图所示.
(2)将各平面图形折起后的空间图形如下图所示.
变式训练3 解 (1)五棱柱;(2)五棱锥;(3)三棱台.如图所示.
课时作业
1.C 2.C 3.A 4.A 5.D
6.①② 7.①②③
8.解 截面BCFE上方部分是棱柱,为棱柱BEB′—CFC′,其中△BEB′和△CFC′是底面.
截面BCFE下方部分也是棱柱,为棱柱ABEA′—DCFD′,其中四边形ABEA′和四边形DCFD′是底面.
9.解 以边AD所在直线为旋转轴,旋转一周后所得的几何体如图1;以边AB所在直线为旋转轴,旋转一周所得的几何体如图2;以边CD所在直线为旋转轴,旋转一周所得的几何体如图3;其中图1为圆台;图2为圆柱和圆锥的组合体;图3是将一个大圆柱挖去一个圆锥而得到的几何体.
自主学习
1.能根据圆柱、圆锥、圆台和球的定义及结构特征,掌握它们的相关概念和表示方法.
2.能根据棱柱、棱锥、棱台的定义和结构特征,掌握它们的相关概念、分类和表示方法.
1.以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面叫作________,球面所围成的几何体叫作________,简称______.半圆的圆心叫作________.
用一个平面去截一个球,截面是圆面.球面被经过球心的平面截得的圆叫作大圆.
2.分别以矩形的一边、直角三角形的一条直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫作________________________.
3.在旋转轴上这条边的长度叫作它们的高,垂直于旋转轴的边旋转而成的圆面叫作它们的________,不垂直于旋转轴的边旋转而成的曲面叫作它们的________,无论转到什么位置,这条边都叫作侧面的________.
4.棱柱的结构特征:两个面____________,其余各面都是__________,并且每相邻两个四边形的公共边都________________,由这些面围成的几何体叫做棱柱.侧棱垂直于底面的棱柱叫作____________,底面是正多边形的直棱柱叫作__________.
5.棱锥的结构特征:有一个面是__________,其余各面是
________________________________,这些面围成的几何体叫棱锥.如果棱锥的底面是____________,且各侧面________,就称作正棱锥.
6.棱台的结构特征:用一个__________棱锥底面的平面去截棱锥,________________
之间的部分叫作棱台.
对点讲练
旋转体的有关概念
例1 有以下命题:
①以直角三角形一边为旋转轴,旋转所得的旋转体是圆锥;②以直角梯形的一条腰所在直线为旋转轴,旋转所得的几何体是圆台;③圆柱、圆锥、圆台的底面都是圆;④分别以矩形两条不同的边所在直线为旋转轴,将矩形旋转,所得的两个圆柱可能是两个不同的圆柱.
其中正确的个数有( )
A.1 B.2 C.3 D.4
点评 本题是考查圆柱、圆锥、圆台概念的理解问题.对几何体的概念理解要到位,稍有疏忽都会造成错误的判断,做题时要注意哪条边所在直线为旋转轴,必须清楚地认识到:以直角三角形的一条直角边所在直线为旋转轴旋转得圆锥,以斜边为旋转轴旋转就是两个圆锥的组合体;以直角梯形垂直于底的腰所在直线为旋转轴旋转得圆台,以斜腰所在直线为旋转轴把直角梯形旋转一周得两个圆锥和一个圆台的组合体.
变式训练1 下列命题中,错误的是( )
A.圆柱的轴截面是过母线的截面中面积最大的一个
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.圆台的所有平行于底面的截面都是圆面
D.圆锥所有的轴截面是全等的等腰三角形
多面体的有关概念
例2 给出下列几个命题:
①棱柱的侧面都是平行四边形;
②棱锥的侧面为三角形,且所有侧面都有一个公共顶点;
③多面体至少有四个面;
④棱台的侧棱所在直线均相交于同一点.
其中,假命题的个数是( )
A.0 B.1 C.2 D.3
点评 只有理解并掌握好各种简单多面体的概念,以及相应的结构特征,才能不至于被各个命题的表面假象所迷惑,从而对问题做出正确的判断.
变式训练2 有四个命题:
①各侧面是全等的等腰三角形的四棱锥是正四棱锥;②底面是正多边形的棱锥是正棱锥;③棱锥的所有面可能是直角三角形;④四棱锥中侧面最多有四个直角三角形.
正确的命题有________________.(填序号)
几何体的结构特征
例3 (1)请画出下图所示的几何体的表面展开图.
(2)根据下图所给的平面图形,画出立体图.
点评 (1)要画一个多面体的表面展开图,可以先用硬纸做一个相应的多面体的实物模型,然后沿着某些棱把它剪开,并铺成平面图形,进而画出相应的平面图形.将多面体的表面展开成平面图形,有利于我们解决与多面体表面有关的问题.
(2)平面图形的折叠问题实质上是多面体的表面展开问题的逆向问题(即逆向过程).这两类问题都是立体几何中的基本问题,我们必须熟练掌握折叠与展开这两个基本功,并准确地画出在折叠和展开的前后的平面图形和立体图形,进而找到折叠和展开前后的变化的量和不变的量.
变式训练3 如图是三个几何体的侧面展开图,请问各是什么几何体?
课时作业
一、选择题
1.截一个几何体,各个截面都是圆面,则这个几何体一定是( )
A.圆柱 B.圆锥 C.球 D.圆台
2.有下列四个命题:
①圆柱是将矩形旋转一周所得的几何体;
②以直角三角形的一边为旋转轴,旋转所得几何体是圆锥;
③圆台的任意两条母线的延长线,可能相交也可能不相交;
④圆锥的轴截面是等腰三角形.
其中错误命题的个数是( )
A.1 B.2 C.3 D.4
3.下图是由哪个平面图形旋转得到的( )
4.如图所示,将装有水的长方体槽固定底面一边后将水槽倾斜一个小角度,则倾斜后水槽中的水形成的几何体是( )
A.棱柱 B.棱台
C.棱柱与棱锥组合体 D.不能确定
5.下图中不可能围成正方体的是( )
二、填空题
6.在下面4个平面图形中,哪几个是下面各侧棱都相等的四面体的展开图?其序号是______.(把你认为正确的序号都填上)
7.下列命题中:①用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫棱台;②棱台的各侧棱延长后一定相交于一点;③圆台可以看作直角梯形绕与底边垂直的腰所在直线旋转而成的几何体;④半圆绕其直径所在直线旋转一周形成球.正确命题的序号为__________.
三、解答题
8.如图所示为长方体ABCD—A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由.
9.四边形ABCD为直角梯形,分别以边AD、边AB、边CD所在直线为轴旋转,分析所形成的三个几何体的结构特征.
第一章 立体几何
§1 简单几何体
答案
自学导引
1.球面 球体 球 球心
2.圆柱、圆锥、圆台
3.底面 侧面 母线
4.互相平行 四边形 互相平行 直棱柱 正棱柱
5.多边形 有一个公共顶点的三角形 正多边形 全等
6.平行于 底面与截面
对点讲练
例1 A [圆锥是以直角三角形的一条直角边所在直线为旋转轴的,如果以斜边所在直线为旋转轴旋转,那就变成一个组合体了,故①错误;圆台是以直角梯形与底边垂直的腰所在直线为旋转轴的,故②错误;圆柱、圆锥、圆台的底面为圆面,③错误;根据圆柱的定义可知,无论以矩形的哪条边所在直线为旋转轴,旋转所得的曲面围成的几何体都是圆柱,但它们并不一定是相同的圆柱,故④正确,因此正确的命题有1个.]
变式训练1 B
例2 A [显然命题①、②均是真命题.
对于命题③,显然一个图形要成为空间几何体,它至少需有四个顶点,因为三个顶点只围成一个平面图形是三角形,当有四个顶点时,易知它可围成四个面,因而一个多面体至少应有四个面,而且这样的面必是三角形,故命题③是真命题.
对于命题④,棱台的侧棱所在的直线就是截得原棱锥的侧棱所在的直线,而棱锥的侧棱都有一个公共的点,它便是棱锥的顶点,于是棱台的侧棱所在的直线均相交于同一点,故命题④为真命题.]
变式训练2 ③④
例3 解 (1)将立体图形沿着某些棱剪开,然后伸展到平面上.展开图如图所示.
(2)将各平面图形折起后的空间图形如下图所示.
变式训练3 解 (1)五棱柱;(2)五棱锥;(3)三棱台.如图所示.
课时作业
1.C 2.C 3.A 4.A 5.D
6.①② 7.①②③
8.解 截面BCFE上方部分是棱柱,为棱柱BEB′—CFC′,其中△BEB′和△CFC′是底面.
截面BCFE下方部分也是棱柱,为棱柱ABEA′—DCFD′,其中四边形ABEA′和四边形DCFD′是底面.
9.解 以边AD所在直线为旋转轴,旋转一周后所得的几何体如图1;以边AB所在直线为旋转轴,旋转一周所得的几何体如图2;以边CD所在直线为旋转轴,旋转一周所得的几何体如图3;其中图1为圆台;图2为圆柱和圆锥的组合体;图3是将一个大圆柱挖去一个圆锥而得到的几何体.
