华东师大版七年级下册数学 9.2 多边形的内角和与外角和-探究四边形的内角和教案
文档属性
| 名称 | 华东师大版七年级下册数学 9.2 多边形的内角和与外角和-探究四边形的内角和教案 |  | |
| 格式 | doc | ||
| 文件大小 | 790.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 07:42:55 | ||
图片预览

文档简介
9.2多边形的内角和——探究四边形的内角和
一、教材分析
《多边形的内角和》是华师大版七年级下期第九章第二节的内容. 多边形的内角和是在三角形内角和知识基础上的拓广和发展,是从特殊到一般的深化,是后面学习多边形镶嵌的基础,也是今后学习空间几何的基础,对发展学生的空间观念和几何直觉有很大的帮助. 为了更透彻地学习多边形的内角和,本节课将以四边形为例,学习它的内角和的证明方法,为后面多边形的学习打下扎实的基础,学生在后续的学习可以类比这些方法进行探究.本节课着重让学生体会如何将四边形转化为三角形,化未知为已知的转化思想.也让学生感受到很多数学结论的形成都是通过动手实践、猜想、探究、推理而得出.
二、学情分析
本节课之前学生对三角形、特殊四边形的内角和已经有了一定的理解和认识. 估计学生在探究任意四边形内角和时会想到量、拼、分的方法,但是分割四边形为三角形这一过程会是学生学习的难点,在探究的过程中教师要想办法把难点分散,有利于学生对本课知识的学习和掌握.
三、教学目标
知识与技能:1、掌握并理解四边形的内角和的计算方法,并能用其解决一些简单的问题;2、通过四边形内角和计算公式的推导,体验转化的数学思想.
过程与方法:1、让学生经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力. 2、通过把四边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法. 3、通过探索四边形的内角和,让学生尝试从不同的角度寻求解决问题的方法,并能有效地解决问题.
情感态度与价值观:通过动手实践、相互间的交流,进一步激发学习热情和求知欲望.同时,体验猜想得到证实的成就感,在解题中感受生活中数学的存在,体验数学充满探索和创造.
四、教学重点与难点
重点:四边形的内角和的推导及运用.
难点:四边形的内角和的推导.
五、教学方法
动手实践、自主探究、合作交流
六、教学过程
(一)创设情景,导入新知
1、(教师播放自制的微视频配上欢快的音乐和旁白)同学们,我们说数学来源于生活而又服务于生活,勤劳的小蜜蜂筑建了奇妙的六面体结构蜂窝;建筑师们利用多边形设计创造了许多雄伟壮观的建筑物;我们北京奥运会伟大的水立方也是由无数多个大小不同的多边形组成的. 我们可以真切的感悟到数学就在我们的身边,生活离不开数学,离不开多边形,今天就让我们一起来探究多边形的奥秘,学习四边形的内角和.
设计意图:情景导入是本节课的一个亮点,选择自己制作剪切了一段视频插入到PPT中,它简单包括三方面内容:蜜蜂采蜜建筑蜂巢;市政规划建设;北京水立方. 学生通过视频既能认识感知多边形在生活当中的存在与应用,也能为下节课多边形的镶嵌埋下伏笔. 再插入欢快的音乐,配上老师的解说,一下让学生充满好奇感. 在观看的过程中学生主动地去体会,去发现多边形的知识. 学生有了学习的兴趣,后面的学习活动不再是一种负担,而是一种享受、一种愉快的体验.
2、生活与数学
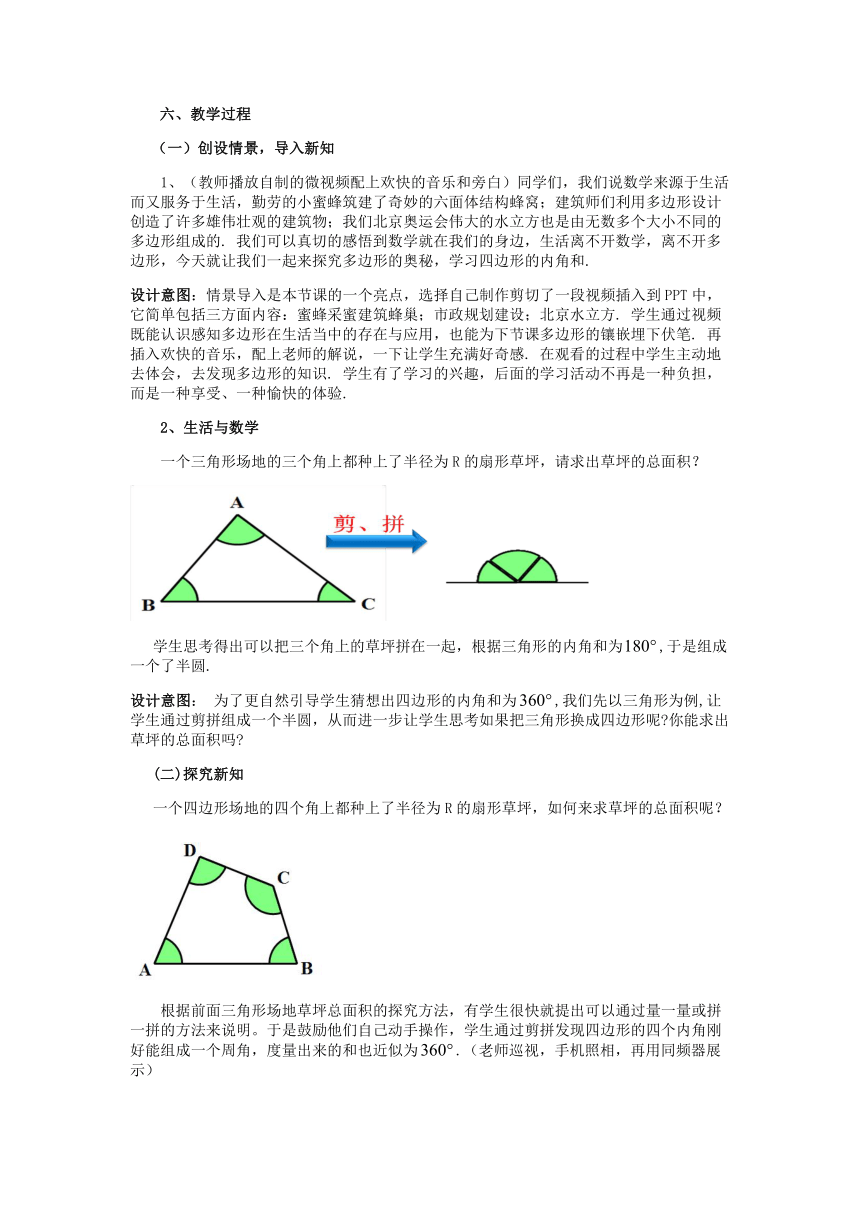
一个三角形场地的三个角上都种上了半径为R的扇形草坪,请求出草坪的总面积?
学生思考得出可以把三个角上的草坪拼在一起,根据三角形的内角和为,于是组成一个了半圆.
设计意图: 为了更自然引导学生猜想出四边形的内角和为,我们先以三角形为例,让学生通过剪拼组成一个半圆,从而进一步让学生思考如果把三角形换成四边形呢 你能求出草坪的总面积吗
(二)探究新知
一个四边形场地的四个角上都种上了半径为R的扇形草坪,如何来求草坪的总面积呢?
根据前面三角形场地草坪总面积的探究方法,有学生很快就提出可以通过量一量或拼一拼的方法来说明。于是鼓励他们自己动手操作,学生通过剪拼发现四边形的四个内角刚好能组成一个周角,度量出来的和也近似为.(老师巡视,手机照相,再用同频器展示)
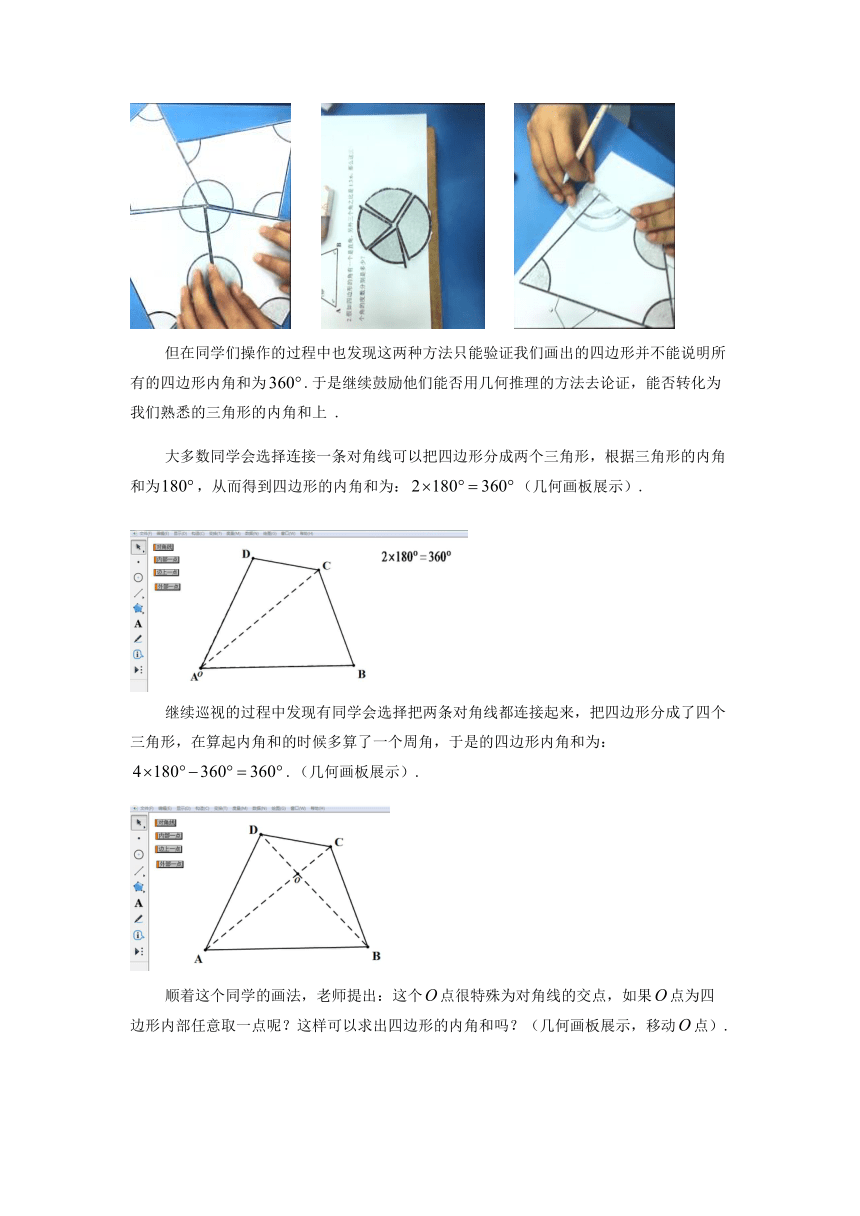
但在同学们操作的过程中也发现这两种方法只能验证我们画出的四边形并不能说明所有的四边形内角和为.于是继续鼓励他们能否用几何推理的方法去论证,能否转化为我们熟悉的三角形的内角和上 .
大多数同学会选择连接一条对角线可以把四边形分成两个三角形,根据三角形的内角和为,从而得到四边形的内角和为:(几何画板展示).
继续巡视的过程中发现有同学会选择把两条对角线都连接起来,把四边形分成了四个三角形,在算起内角和的时候多算了一个周角,于是的四边形内角和为:.(几何画板展示).
顺着这个同学的画法,老师提出:这个点很特殊为对角线的交点,如果点为四边形内部任意取一点呢?这样可以求出四边形的内角和吗?(几何画板展示,移动点).
同学们发现这种方法和前面的类似,而且更具有一般性。也可以得到四边形内角和为:.
学生变得越来越有积极性,继续提问:我们可以从顶点出发引对角线分三角形,也可以从内部任意一点出发分三角形,我们还有什么方法呢?鼓励学生继续探究.
于是有同学提出可以从边上取一点来分三角形,这样可以把四边形分成三个三角形,算内角和时多算了一个平角,于是的到四边形的内角和为:.(几何画板展示)
也有极个别的同学想到了可以在四边形外部取一点来连接形成三角形,但这种方法很多同学不知道怎么去说明,于是选择板书给学生们讲解.仔细观察也不难发现图中有四个三角形,与四边形内角有关的是、、,而这三个三角形多算的内角恰好是的内角和.于是得到四边形内角和为:(几何画板展示)
除了以上几种方法外,有个同学还提出了以下这种方法.
过作交于.根据,可得,,的三个内角与和的这组同旁内角恰好就是四边形的四个内角,它们的和为.这种方法也用得比较巧妙,充分联系了前面已有的知识.
师生共同总结以上这些方法都是将我们的四边形转化为三角形,其目的都是为了化未知为已知,体现了数学中的转化思想.
设计意图:数学教学中,思维能力的培养是核心,这要求教师要加强开放式问题的教学,提倡探究式学习,强化合情推理的训练,让学生通过观察、猜想、操作、类比、转化、归纳得出结论,将教法改革与学法指导结合起来,使数学学习成为再发现、再创造的过程.让学生在自主探究中去积累数学活动经验.在探究四边形的内角和时,同学们表现得十分精彩,各种方法,有些方法老师也没想到,可见给学生以自由想象、自由发挥、自主探索的时间和空间,必定会碰撞出思维的火花.这也为下节课探究多边形的内角和做下了很好的铺垫.
(三)巩固与应用
例1.求下列图形中x的值.
例2.假如四边形的角有一个是直角,另外三个角之比是1:3:6,那么这三个角的度数分别是多少?
设计意图:学生通过练习巩固所学知识,使学生获得成功感,在“用”中积累数学活动经验.
(四)收获与体会
1.这节课我们学习了哪些知识?
2.掌握了哪些基本技能?
3.获得了哪些体验?
4.体会到了哪些数学思想、方法?
(五)作业布置
课本第86页练习
(六)板书设计
探究四边形的内角和
一、1.三角形的内角和为.
2.四边形(未知) 三角形(已知) 转化思想
3.四边形的内角和为.
二、巩固与练习
例1 例2
七、课后反思
优点:1.本节课的导入是个亮点,欢快的音乐,配上老师自制剪切的视频,一下就调动起学生的兴趣,让学生充满了好奇感. 2.在探究四边形内角和时,让学生通过观察、猜想、操作、转化、归纳得出结论,使数学学习成为再发现、再创造的过程. 充分体现了双主共学的理念,即学生的主体地位和教师的主导作用. 3.转化、化归的数学思想贯穿整个教学过程,让教学不仅仅停留在知识的讲解上,更加注重培养学生的数学思想和方法,积累数学活动经验. 4.同频器,微视频,PPT,几何画板的应用,充分体现了现代信息技术在数学教学中的辅助作用.
不足:1.整个教学过程中可以给学生提供更多的展现自己的机会. 2.在探究四边形的内角和时对学生错误的证明方法应该更好地去点拨、引导、纠正,充分利用这些“错误的资源”.
一、教材分析
《多边形的内角和》是华师大版七年级下期第九章第二节的内容. 多边形的内角和是在三角形内角和知识基础上的拓广和发展,是从特殊到一般的深化,是后面学习多边形镶嵌的基础,也是今后学习空间几何的基础,对发展学生的空间观念和几何直觉有很大的帮助. 为了更透彻地学习多边形的内角和,本节课将以四边形为例,学习它的内角和的证明方法,为后面多边形的学习打下扎实的基础,学生在后续的学习可以类比这些方法进行探究.本节课着重让学生体会如何将四边形转化为三角形,化未知为已知的转化思想.也让学生感受到很多数学结论的形成都是通过动手实践、猜想、探究、推理而得出.
二、学情分析
本节课之前学生对三角形、特殊四边形的内角和已经有了一定的理解和认识. 估计学生在探究任意四边形内角和时会想到量、拼、分的方法,但是分割四边形为三角形这一过程会是学生学习的难点,在探究的过程中教师要想办法把难点分散,有利于学生对本课知识的学习和掌握.
三、教学目标
知识与技能:1、掌握并理解四边形的内角和的计算方法,并能用其解决一些简单的问题;2、通过四边形内角和计算公式的推导,体验转化的数学思想.
过程与方法:1、让学生经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力. 2、通过把四边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法. 3、通过探索四边形的内角和,让学生尝试从不同的角度寻求解决问题的方法,并能有效地解决问题.
情感态度与价值观:通过动手实践、相互间的交流,进一步激发学习热情和求知欲望.同时,体验猜想得到证实的成就感,在解题中感受生活中数学的存在,体验数学充满探索和创造.
四、教学重点与难点
重点:四边形的内角和的推导及运用.
难点:四边形的内角和的推导.
五、教学方法
动手实践、自主探究、合作交流
六、教学过程
(一)创设情景,导入新知
1、(教师播放自制的微视频配上欢快的音乐和旁白)同学们,我们说数学来源于生活而又服务于生活,勤劳的小蜜蜂筑建了奇妙的六面体结构蜂窝;建筑师们利用多边形设计创造了许多雄伟壮观的建筑物;我们北京奥运会伟大的水立方也是由无数多个大小不同的多边形组成的. 我们可以真切的感悟到数学就在我们的身边,生活离不开数学,离不开多边形,今天就让我们一起来探究多边形的奥秘,学习四边形的内角和.
设计意图:情景导入是本节课的一个亮点,选择自己制作剪切了一段视频插入到PPT中,它简单包括三方面内容:蜜蜂采蜜建筑蜂巢;市政规划建设;北京水立方. 学生通过视频既能认识感知多边形在生活当中的存在与应用,也能为下节课多边形的镶嵌埋下伏笔. 再插入欢快的音乐,配上老师的解说,一下让学生充满好奇感. 在观看的过程中学生主动地去体会,去发现多边形的知识. 学生有了学习的兴趣,后面的学习活动不再是一种负担,而是一种享受、一种愉快的体验.
2、生活与数学
一个三角形场地的三个角上都种上了半径为R的扇形草坪,请求出草坪的总面积?
学生思考得出可以把三个角上的草坪拼在一起,根据三角形的内角和为,于是组成一个了半圆.
设计意图: 为了更自然引导学生猜想出四边形的内角和为,我们先以三角形为例,让学生通过剪拼组成一个半圆,从而进一步让学生思考如果把三角形换成四边形呢 你能求出草坪的总面积吗
(二)探究新知
一个四边形场地的四个角上都种上了半径为R的扇形草坪,如何来求草坪的总面积呢?
根据前面三角形场地草坪总面积的探究方法,有学生很快就提出可以通过量一量或拼一拼的方法来说明。于是鼓励他们自己动手操作,学生通过剪拼发现四边形的四个内角刚好能组成一个周角,度量出来的和也近似为.(老师巡视,手机照相,再用同频器展示)
但在同学们操作的过程中也发现这两种方法只能验证我们画出的四边形并不能说明所有的四边形内角和为.于是继续鼓励他们能否用几何推理的方法去论证,能否转化为我们熟悉的三角形的内角和上 .
大多数同学会选择连接一条对角线可以把四边形分成两个三角形,根据三角形的内角和为,从而得到四边形的内角和为:(几何画板展示).
继续巡视的过程中发现有同学会选择把两条对角线都连接起来,把四边形分成了四个三角形,在算起内角和的时候多算了一个周角,于是的四边形内角和为:.(几何画板展示).
顺着这个同学的画法,老师提出:这个点很特殊为对角线的交点,如果点为四边形内部任意取一点呢?这样可以求出四边形的内角和吗?(几何画板展示,移动点).
同学们发现这种方法和前面的类似,而且更具有一般性。也可以得到四边形内角和为:.
学生变得越来越有积极性,继续提问:我们可以从顶点出发引对角线分三角形,也可以从内部任意一点出发分三角形,我们还有什么方法呢?鼓励学生继续探究.
于是有同学提出可以从边上取一点来分三角形,这样可以把四边形分成三个三角形,算内角和时多算了一个平角,于是的到四边形的内角和为:.(几何画板展示)
也有极个别的同学想到了可以在四边形外部取一点来连接形成三角形,但这种方法很多同学不知道怎么去说明,于是选择板书给学生们讲解.仔细观察也不难发现图中有四个三角形,与四边形内角有关的是、、,而这三个三角形多算的内角恰好是的内角和.于是得到四边形内角和为:(几何画板展示)
除了以上几种方法外,有个同学还提出了以下这种方法.
过作交于.根据,可得,,的三个内角与和的这组同旁内角恰好就是四边形的四个内角,它们的和为.这种方法也用得比较巧妙,充分联系了前面已有的知识.
师生共同总结以上这些方法都是将我们的四边形转化为三角形,其目的都是为了化未知为已知,体现了数学中的转化思想.
设计意图:数学教学中,思维能力的培养是核心,这要求教师要加强开放式问题的教学,提倡探究式学习,强化合情推理的训练,让学生通过观察、猜想、操作、类比、转化、归纳得出结论,将教法改革与学法指导结合起来,使数学学习成为再发现、再创造的过程.让学生在自主探究中去积累数学活动经验.在探究四边形的内角和时,同学们表现得十分精彩,各种方法,有些方法老师也没想到,可见给学生以自由想象、自由发挥、自主探索的时间和空间,必定会碰撞出思维的火花.这也为下节课探究多边形的内角和做下了很好的铺垫.
(三)巩固与应用
例1.求下列图形中x的值.
例2.假如四边形的角有一个是直角,另外三个角之比是1:3:6,那么这三个角的度数分别是多少?
设计意图:学生通过练习巩固所学知识,使学生获得成功感,在“用”中积累数学活动经验.
(四)收获与体会
1.这节课我们学习了哪些知识?
2.掌握了哪些基本技能?
3.获得了哪些体验?
4.体会到了哪些数学思想、方法?
(五)作业布置
课本第86页练习
(六)板书设计
探究四边形的内角和
一、1.三角形的内角和为.
2.四边形(未知) 三角形(已知) 转化思想
3.四边形的内角和为.
二、巩固与练习
例1 例2
七、课后反思
优点:1.本节课的导入是个亮点,欢快的音乐,配上老师自制剪切的视频,一下就调动起学生的兴趣,让学生充满了好奇感. 2.在探究四边形内角和时,让学生通过观察、猜想、操作、转化、归纳得出结论,使数学学习成为再发现、再创造的过程. 充分体现了双主共学的理念,即学生的主体地位和教师的主导作用. 3.转化、化归的数学思想贯穿整个教学过程,让教学不仅仅停留在知识的讲解上,更加注重培养学生的数学思想和方法,积累数学活动经验. 4.同频器,微视频,PPT,几何画板的应用,充分体现了现代信息技术在数学教学中的辅助作用.
不足:1.整个教学过程中可以给学生提供更多的展现自己的机会. 2.在探究四边形的内角和时对学生错误的证明方法应该更好地去点拨、引导、纠正,充分利用这些“错误的资源”.
