湖南省邵阳市2021-2022学年高二下学期入学考试数学试题(Word版含答案)
文档属性
| 名称 | 湖南省邵阳市2021-2022学年高二下学期入学考试数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 658.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览




文档简介
邵阳市2021-2022学年高二下学期入学考试
数学试卷
时量:120分钟 总分:150分
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知为虚数单位,复数,则的实部与虚部之差为( )
A.1 B.0 C. -1 D.
2.设a、b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知直线y = 2x是△ABC中∠C的平分线所在的直线,若A,B的坐标分别是(-4,2),(3,1),则点C的坐标为( )
A.(-2,4) B.(-2,-4) C.(2,4) D.(2,-4)
4.我国古代数学名著《算法统宗》中有如下问题:“诸葛亮领八员将,每将又分八个营,每营里面排八阵,每阵先锋有八人,每人旗头俱八个,每个旗头八队成,每队更该八个甲,每个甲头八个兵.”则该问题中将官、先锋、旗头、队长、甲头、士兵共有( )
A.人 B.人
C.人 D.人
5.若函数f (x)=在区间(2,3)内有极值点,则实数a的取值范围是( )
A. B.()
C.(-∞,)∪(,+∞) D. (-∞,∪,+∞)
6.已知函数是定义在上的偶函数,且在上单调递增,则( )
A. B.
C. D.
7.设,是双曲线的两个焦点,是上一点,若,且的最小内角为,则的离心率为( )
A. B. C. D.
8.已知,则的取值范围是( )
A. B.
C. D.
二 多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.对于函数f (x)= ,下列说法正确的有( )
A.f (x)在x=1处取得极大值 B.f (x)有两个不同的零点
C.f (4)<f ()<f (3) D.>2
10.已知圆M:+=1,直线l:y=kx,下列四个命题为真命题的是( )
A.对任意实数k和,直线和圆相切
B.对任意实数k和,直线和圆有公共点
C.对任意实数,必存在实数k使得直线与圆相切
D. 对任意实数k,必存在实数使得直线与圆相切
11.已知函数使得≤成立,且在区间上的值域为则实数的取值可能是( )
A. B. C. 1 D.
12.如图1,在边长为2的正方形ABCD中,,,分别为BC,CD,BE的中点,沿 及把这个正方形折成一个四面体,使得B、C、D三点重合于S,得到四面体(如图2).下列结论正确的是( )
A.四面体的外接球体积为
B.顶点在面上的射影为的重心
C.与面所成角的正切值为
D.过点的平面截四面体的外接球所得截面圆的面积的取值范围是
三 填空题:(本题共4小题,每小题5分,共20分)
13.若函数在区间[2,+∞)上是增函数,则实数的取值范围是________.
14.若,且,则
15.已知函数,则关于x的不等式的解集为______________.
16.设抛物线=4x的焦点为F,过F的直线l交抛物线于A,B两点,过AB的中点M作y轴的垂线与抛物线在第一象限内交于点P,若|PF|=,则直线l的方程为_____________.
四、解答题:(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(满分10分)
在中,角,,的对边分别为,,,且.
(1)求角的大小;
(2)已知外接圆半径,且,求的周长.
18.(满分12分)
已知数列是等差数列,,,数列的前项和为,且.
(Ⅰ)求数列、的通项公式;
(Ⅱ)记,若数列的前项和为,证明:.
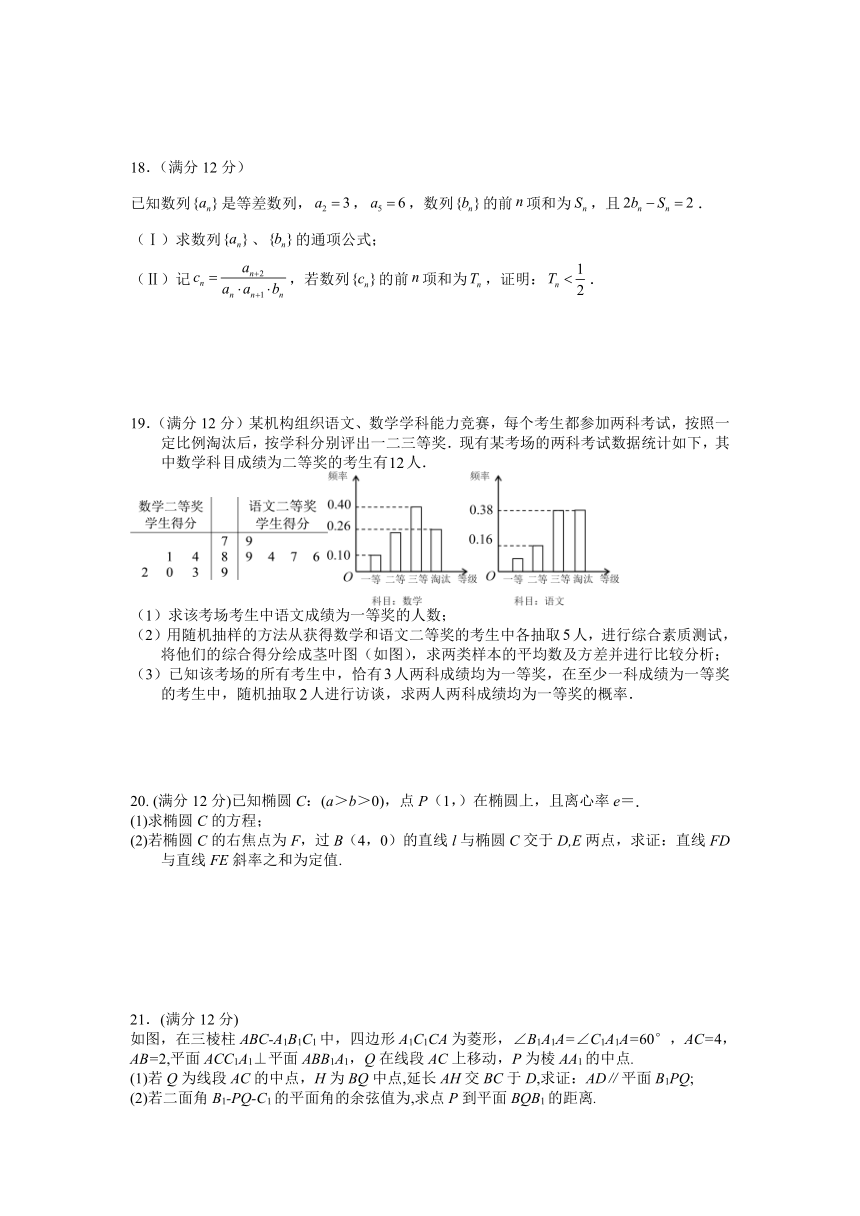
19.(满分12分)某机构组织语文、数学学科能力竞赛,每个考生都参加两科考试,按照一定比例淘汰后,按学科分别评出一二三等奖.现有某考场的两科考试数据统计如下,其中数学科目成绩为二等奖的考生有人.
(1)求该考场考生中语文成绩为一等奖的人数;
(2)用随机抽样的方法从获得数学和语文二等奖的考生中各抽取人,进行综合素质测试,将他们的综合得分绘成茎叶图(如图),求两类样本的平均数及方差并进行比较分析;
(3)已知该考场的所有考生中,恰有人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取人进行访谈,求两人两科成绩均为一等奖的概率.
20. (满分12分)已知椭圆C:(a>b>0),点P(1,)在椭圆上,且离心率e=.
(1)求椭圆C的方程;
(2)若椭圆C的右焦点为F,过B(4,0)的直线l与椭圆C交于D,E两点,求证:直线FD与直线FE斜率之和为定值.
21.(满分12分)
如图,在三棱柱ABC-A1B1C1中,四边形A1C1CA为菱形,∠B1A1A=∠C1A1A=60°,AC=4,AB=2,平面ACC1A1⊥平面ABB1A1,Q在线段AC上移动,P为棱AA1的中点.
(1)若Q为线段AC的中点,H为BQ中点,延长AH交BC于D,求证:AD∥平面B1PQ;
(2)若二面角B1-PQ-C1的平面角的余弦值为,求点P到平面BQB1的距离.
22. (满分12分)已知函数f (x)=aln x-ax-3(a∈R).
(1)求函数f (x)的单调区间;
(2)若函数y=f (x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2在区间(t,3)上总不是单调函数,求m的取值范围.
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知为虚数单位,复数,则的实部与虚部之差为( )
A. 1 B.0
C. D.
【答案】D
【解析】:
复数,∴
2.设a、b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的( C )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知直线y = 2x是△ABC中∠C的平分线所在的直线,若A,B的坐标分别是(-4,2),(3,1),则点C的坐标为( C )
A.(-2,4) B.(-2,-4) C.(2,4) D.(2,-4)
4. 我国古代数学名著《算法统宗》中有如下问题:“诸葛亮领八员将,每将又分八个营,每营里面排八阵,每阵先锋有八人,每人旗头俱八个,每个旗头八队成,每队更该八个甲,每个甲头八个兵.”则该问题中将官、先锋、旗头、队长、甲头、士兵共有( )
A.人 B.人
C.人 D.人
【答案】D
【解析】由题意可得将官、营、阵、先锋、旗头、队长、甲头、士兵依次成等比数列,且首项为8,公比也是8,所以将官、先锋、旗头、队长、甲头、士兵共有:
,故选D.
5.5.若函数f (x)=在区间(2,3)内有极值点,则实数a的取值范围是( B )
A. B.()
C.(-∞,)∪(,+∞) D. (-∞,∪,+∞)
6.已知函数是定义在上的偶函数,且在上单调递增,则( )
A. B.
C. D.
【答案】C
【解析】根据题意,函数是定义在上的偶函数,则,,有,又由在上单调递增,则有,故选C.
7.设,是双曲线的两个焦点,是上一点,若,且的最小内角为,则的离心率为( )
A. B.
C. D.
【答案】C
【解析】因为,是双曲线的两个焦点,是双曲线上一点,且满足,
不妨设是双曲线右支上的一点,由双曲线的定义可知,
所以,,,
,,为最小边,
的最小内角,根据余弦定理,
,
即,
,,所以,故选C.
8. 已知,则的取值范围是( )
A. B.
C. D.
【答案】A
【解析】:据题意有,而故选A.
二 多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.对于函数f (x)= ,下列说法正确的有( AC )
A.f (x)在x=1处取得极大值 B.f (x)有两个不同的零点
C.f (4)<f ()<f (3) D.>2
10.已知圆M:+=1,直线l:y=kx,下列四个命题为真命题的是( BD )
A.对任意实数k和,直线和圆相切
B.对任意实数k和,直线和圆有公共点
C.对任意实数,必存在实数k使得直线与圆相切
D. 对任意实数k,必存在实数使得直线与圆相切
11.已知函数使得≤成立,且在区间上的值域为则实数的取值可能是( CD )
A. B. C. 1 D.
12.如图1,在边长为2的正方形中,,,分别为,,的中点,沿 及把这个正方形折成一个四面体,使得 三点重合于,得到四面体(如图2).下列结论正确的是( )
A.四面体的外接球体积为
B.顶点在面上的射影为的重心
C.与面所成角的正切值为
D.过点的平面截四面体的外接球所得截面圆的面积的取值范围是
【答案】ACD
【详解】
对于A项,易知 两两垂直,故可以补成长方体,其体对角线长,
外接球半径,故外接球体积为,
故A项正确;
对于B项,由于 两两垂直,故在面上的射影为的垂心,
理由如下:如图,过点作平面,交平面于点,
因为平面,平面,所以,
又因为,,,都在平面内,且相交于点,
所以平面,又平面,所以,
又,所以平面,又平面,所以.
同理可证,,所以在面上的射影为的垂心.
故B项错误;
对于C项,设为中点,则,,,
故平面,故平面平面,所以在平面上的射影为,
与平面所成角为,,,,,
故C项正确;
对于D项,设为四面体的外接球球心,平面,连接,,
当过点的截面经过球心时截面圆面积最大,面积为;
当垂直截面圆时,截面圆面积最小,
此时,,,
,截面圆面积为,
得截面圆面积取值范围是.
故D项正确.
故选:ACD.
三 填空题:(本题共4小题,每小题5分,共20分)
若函数在区间[2,+∞)上是增函数,则实数的取值范围是 (-4,4] .
14.若,且,则
15. 已知函数,则关于的不等式的解集为______________.
【答案】
【解析】令则为上的单增奇函数,
16.设抛物线=4x的焦点为F,过F的直线l交抛物线于A,B两点,过AB的中点M作y轴的垂线与抛物线在第一象限内交于点P,若|PF|=,则直线l的方程为_____________.
17.(本小题满分10分)
在中,角,,的对边分别为,,,且.
(1)求角的大小;
(2)已知外接圆半径,且,求的周长.
【答案】(1);(2).
【解析】(1),,
即,,
又,.……………………………………………………………………………………….5分
(2),,,∴由余弦定理可得,,
∴,∵,所以得,∴周长.…………………………………………10分
18.(本小题满分12分)
已知数列是等差数列,,,数列的前项和为,且.
(Ⅰ)求数列、的通项公式;
(Ⅱ)记,若数列的前项和为,证明:.
【答案】见解析
【解析】(1)由已知得,解得,所以…………………………2分
当时,, (1)…………………………………………3分
,当时, (2)………………………5分
由(1),(2)得…………………………………………………………………6分
(Ⅱ)由(Ⅰ)知,所以………………………………………………8分
………………………………………………………10分
…………………………………………………………………………………………11分
…………………………………………………………………………………12分
19.某机构组织语文、数学学科能力竞赛,每个考生都参加两科考试,按照一定比例淘汰后,按学科分别评出一二三等奖.现有某考场的两科考试数据统计如下,其中数学科目成绩为二等奖的考生有人.
(1)求该考场考生中语文成绩为一等奖的人数;
(2)用随机抽样的方法从获得数学和语文二等奖的考生中各抽取人,进行综合素质测试,将他们的综合得分绘成茎叶图(如图),求两类样本的平均数及方差并进行比较分析;
(3)已知该考场的所有考生中,恰有人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取人进行访谈,求两人两科成绩均为一等奖的概率.
19.【答案】(Ⅰ)由数学成绩为二等奖的考生有人,可得,所以语文成绩为一等奖的考生人............2分
(Ⅱ)设数学和语文两科的平均数和方差分别为,,,
,
,因为,,所以数学二等奖考生较语文二等奖考生综合测试平均分高,但是稳定性较差. ..............7分
(Ⅲ)两科均为一等奖共有人,仅数学一等奖有人,仅语文一等奖有人----9分
设两科成绩都是一等奖的人分别为,只有数学一科为一等奖的人分别是,只有语文一科为一等奖的人是,则随机抽取两人的基本事件空间为 ,共有个,而两人两科成绩均为一等奖的基本事件共个,所以两人的两科成绩均为一等奖的概率. .................12分
20. (满分12分)已知椭圆C:(a>b>0),点P(1,)在椭圆上,且离心率e=.
(1)求椭圆C的方程;
(2)若椭圆C的右焦点为F,过B(4,0)的直线l与椭圆C交于D,E两点,求证:直线FD与直线FE斜率之和为定值.
(1)由题意知,所以a=2c,-=
故椭圆的方程为,
又点P(1,)在椭圆上,代入解得
所以=4,
故椭圆C的方程为.
(2)证明:设直线l的方程为y=k(x-4),D(x1,y1),E(x2,y2),
联立方程组,可得
(3+4k2)x2-32k2x+64k2-12=0,
则,解得<
∴x1+ x2=,x1 x2=,
所以直线FD与直线FE斜率之和为0.
21.如图,在三棱柱ABC-A1B1C1中,四边形A1C1CA为菱形,∠B1A1A=∠C1A1A=60°,AC=4,AB=2,平面ACC1A1⊥平面ABB1A1,Q在线段AC上移动,P为棱AA1的中点.
(1)若Q为线段AC的中点,H为BQ中点,延长AH交BC于D,求证:AD∥平面B1PQ;
(2)若二面角B1-PQ-C1的平面角的余弦值为,求点P到平面BQB1的距离.
(1)证明 如图,取BB1中点E,连接AE,EH.
∵H为BQ中点,∴EH∥B1Q.
在平行四边形AA1B1B中,P,E分别为AA1,BB1的中点,∴AE∥PB1.
又EH∩AE=E,PB1∩B1Q=B1,
∴平面EHA∥平面B1QP.
∵AD 平面EHA,∴AD∥平面B1PQ............................5分
(2)解 连接PC1,AC1,
∵四边形A1C1CA为菱形,
∴AA1=AC=A1C1=4.
又∠C1A1A=60°,
∴△AC1A1为正三角形.
∵P为AA1的中点,∴PC1⊥AA1.
∵平面ACC1A1⊥平面ABB1A1,平面ACC1A1∩平面ABB1A1=AA1,PC1 平面ACC1A1,∴PC1⊥平面ABB1A1,在平面ABB1A1内过点P作PR⊥AA1交BB1于点R.建立如图所示的空间直角坐标系P-xyz,则P(0,0,0),A1(0,2,0),A(0,-2,0),C1(0,0,2),C(0,-4,2),............................7分
设=λ=λ(0,-2,2),λ∈[0,1],
∴Q(0,-2(λ+1),2λ),
∴=(0,-2(λ+1),2λ).
∵A1B1=AB=2,∠B1A1A=60°,
∴B1(,1,0),∴=(,1,0).
设平面PQB1的法向量为m=(x,y,z),
则
得
令x=1,则y=-,z=-,
∴平面PQB1的一个法向量为m=1,-,-,
设平面AA1C1C的法向量为n=(1,0,0),二面角B1-PQ-C1的平面角为θ,则cos θ===.∴λ=或λ=-(舍),......................10分
∴=,∴Q(0,-3,).
又B(,-3,0),∴=(,0,-),∴||==.
连接BP,设点P到平面BQB1的距离为h,则××4××=××4××h,
∴h=,即点P到平面BQB1的距离为....................12分
22.已知函数f(x)=aln x-ax-3(a∈R).
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2·在区间(t,3)上总不是单调函数,求m的取值范围.
[解析] (1)函数f(x)的定义域为(0,+∞),且f′(x)=.
当a>0时,f(x)的增区间为(0,1),减区间为(1,+∞);
当a<0时,f(x)的增区间为(1,+∞),减区间为(0,1);
当a=0时,f(x)不是单调函数.................................5分
(2)由(1)及题意得f′(2)=-=1,即a=-2,
∴f(x)=-2ln x+2x-3,f′(x)=.
∴g(x)=x3+x2-2x,∴g′(x)=3x2+(m+4)x-2.
∵g(x)在区间(t,3)上总不是单调函数,
即g′(x)=0在区间(t,3)上有变号零点.由于g′(0)=-2,
∴
当g′(t)<0,即3t2+(m+4)t-2<0对任意t∈[1,2]恒成立,由于g′(0)<0,故只要g′(1)<0且g′(2)<0,即m<-5且m<-9,即m<-9;
由g′(3)>0,即m>-.
所以-<m<-9.
即实数m的取值范围是...................12分
数学试卷
时量:120分钟 总分:150分
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知为虚数单位,复数,则的实部与虚部之差为( )
A.1 B.0 C. -1 D.
2.设a、b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知直线y = 2x是△ABC中∠C的平分线所在的直线,若A,B的坐标分别是(-4,2),(3,1),则点C的坐标为( )
A.(-2,4) B.(-2,-4) C.(2,4) D.(2,-4)
4.我国古代数学名著《算法统宗》中有如下问题:“诸葛亮领八员将,每将又分八个营,每营里面排八阵,每阵先锋有八人,每人旗头俱八个,每个旗头八队成,每队更该八个甲,每个甲头八个兵.”则该问题中将官、先锋、旗头、队长、甲头、士兵共有( )
A.人 B.人
C.人 D.人
5.若函数f (x)=在区间(2,3)内有极值点,则实数a的取值范围是( )
A. B.()
C.(-∞,)∪(,+∞) D. (-∞,∪,+∞)
6.已知函数是定义在上的偶函数,且在上单调递增,则( )
A. B.
C. D.
7.设,是双曲线的两个焦点,是上一点,若,且的最小内角为,则的离心率为( )
A. B. C. D.
8.已知,则的取值范围是( )
A. B.
C. D.
二 多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.对于函数f (x)= ,下列说法正确的有( )
A.f (x)在x=1处取得极大值 B.f (x)有两个不同的零点
C.f (4)<f ()<f (3) D.>2
10.已知圆M:+=1,直线l:y=kx,下列四个命题为真命题的是( )
A.对任意实数k和,直线和圆相切
B.对任意实数k和,直线和圆有公共点
C.对任意实数,必存在实数k使得直线与圆相切
D. 对任意实数k,必存在实数使得直线与圆相切
11.已知函数使得≤成立,且在区间上的值域为则实数的取值可能是( )
A. B. C. 1 D.
12.如图1,在边长为2的正方形ABCD中,,,分别为BC,CD,BE的中点,沿 及把这个正方形折成一个四面体,使得B、C、D三点重合于S,得到四面体(如图2).下列结论正确的是( )
A.四面体的外接球体积为
B.顶点在面上的射影为的重心
C.与面所成角的正切值为
D.过点的平面截四面体的外接球所得截面圆的面积的取值范围是
三 填空题:(本题共4小题,每小题5分,共20分)
13.若函数在区间[2,+∞)上是增函数,则实数的取值范围是________.
14.若,且,则
15.已知函数,则关于x的不等式的解集为______________.
16.设抛物线=4x的焦点为F,过F的直线l交抛物线于A,B两点,过AB的中点M作y轴的垂线与抛物线在第一象限内交于点P,若|PF|=,则直线l的方程为_____________.
四、解答题:(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(满分10分)
在中,角,,的对边分别为,,,且.
(1)求角的大小;
(2)已知外接圆半径,且,求的周长.
18.(满分12分)
已知数列是等差数列,,,数列的前项和为,且.
(Ⅰ)求数列、的通项公式;
(Ⅱ)记,若数列的前项和为,证明:.
19.(满分12分)某机构组织语文、数学学科能力竞赛,每个考生都参加两科考试,按照一定比例淘汰后,按学科分别评出一二三等奖.现有某考场的两科考试数据统计如下,其中数学科目成绩为二等奖的考生有人.
(1)求该考场考生中语文成绩为一等奖的人数;
(2)用随机抽样的方法从获得数学和语文二等奖的考生中各抽取人,进行综合素质测试,将他们的综合得分绘成茎叶图(如图),求两类样本的平均数及方差并进行比较分析;
(3)已知该考场的所有考生中,恰有人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取人进行访谈,求两人两科成绩均为一等奖的概率.
20. (满分12分)已知椭圆C:(a>b>0),点P(1,)在椭圆上,且离心率e=.
(1)求椭圆C的方程;
(2)若椭圆C的右焦点为F,过B(4,0)的直线l与椭圆C交于D,E两点,求证:直线FD与直线FE斜率之和为定值.
21.(满分12分)
如图,在三棱柱ABC-A1B1C1中,四边形A1C1CA为菱形,∠B1A1A=∠C1A1A=60°,AC=4,AB=2,平面ACC1A1⊥平面ABB1A1,Q在线段AC上移动,P为棱AA1的中点.
(1)若Q为线段AC的中点,H为BQ中点,延长AH交BC于D,求证:AD∥平面B1PQ;
(2)若二面角B1-PQ-C1的平面角的余弦值为,求点P到平面BQB1的距离.
22. (满分12分)已知函数f (x)=aln x-ax-3(a∈R).
(1)求函数f (x)的单调区间;
(2)若函数y=f (x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2在区间(t,3)上总不是单调函数,求m的取值范围.
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知为虚数单位,复数,则的实部与虚部之差为( )
A. 1 B.0
C. D.
【答案】D
【解析】:
复数,∴
2.设a、b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的( C )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知直线y = 2x是△ABC中∠C的平分线所在的直线,若A,B的坐标分别是(-4,2),(3,1),则点C的坐标为( C )
A.(-2,4) B.(-2,-4) C.(2,4) D.(2,-4)
4. 我国古代数学名著《算法统宗》中有如下问题:“诸葛亮领八员将,每将又分八个营,每营里面排八阵,每阵先锋有八人,每人旗头俱八个,每个旗头八队成,每队更该八个甲,每个甲头八个兵.”则该问题中将官、先锋、旗头、队长、甲头、士兵共有( )
A.人 B.人
C.人 D.人
【答案】D
【解析】由题意可得将官、营、阵、先锋、旗头、队长、甲头、士兵依次成等比数列,且首项为8,公比也是8,所以将官、先锋、旗头、队长、甲头、士兵共有:
,故选D.
5.5.若函数f (x)=在区间(2,3)内有极值点,则实数a的取值范围是( B )
A. B.()
C.(-∞,)∪(,+∞) D. (-∞,∪,+∞)
6.已知函数是定义在上的偶函数,且在上单调递增,则( )
A. B.
C. D.
【答案】C
【解析】根据题意,函数是定义在上的偶函数,则,,有,又由在上单调递增,则有,故选C.
7.设,是双曲线的两个焦点,是上一点,若,且的最小内角为,则的离心率为( )
A. B.
C. D.
【答案】C
【解析】因为,是双曲线的两个焦点,是双曲线上一点,且满足,
不妨设是双曲线右支上的一点,由双曲线的定义可知,
所以,,,
,,为最小边,
的最小内角,根据余弦定理,
,
即,
,,所以,故选C.
8. 已知,则的取值范围是( )
A. B.
C. D.
【答案】A
【解析】:据题意有,而故选A.
二 多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.对于函数f (x)= ,下列说法正确的有( AC )
A.f (x)在x=1处取得极大值 B.f (x)有两个不同的零点
C.f (4)<f ()<f (3) D.>2
10.已知圆M:+=1,直线l:y=kx,下列四个命题为真命题的是( BD )
A.对任意实数k和,直线和圆相切
B.对任意实数k和,直线和圆有公共点
C.对任意实数,必存在实数k使得直线与圆相切
D. 对任意实数k,必存在实数使得直线与圆相切
11.已知函数使得≤成立,且在区间上的值域为则实数的取值可能是( CD )
A. B. C. 1 D.
12.如图1,在边长为2的正方形中,,,分别为,,的中点,沿 及把这个正方形折成一个四面体,使得 三点重合于,得到四面体(如图2).下列结论正确的是( )
A.四面体的外接球体积为
B.顶点在面上的射影为的重心
C.与面所成角的正切值为
D.过点的平面截四面体的外接球所得截面圆的面积的取值范围是
【答案】ACD
【详解】
对于A项,易知 两两垂直,故可以补成长方体,其体对角线长,
外接球半径,故外接球体积为,
故A项正确;
对于B项,由于 两两垂直,故在面上的射影为的垂心,
理由如下:如图,过点作平面,交平面于点,
因为平面,平面,所以,
又因为,,,都在平面内,且相交于点,
所以平面,又平面,所以,
又,所以平面,又平面,所以.
同理可证,,所以在面上的射影为的垂心.
故B项错误;
对于C项,设为中点,则,,,
故平面,故平面平面,所以在平面上的射影为,
与平面所成角为,,,,,
故C项正确;
对于D项,设为四面体的外接球球心,平面,连接,,
当过点的截面经过球心时截面圆面积最大,面积为;
当垂直截面圆时,截面圆面积最小,
此时,,,
,截面圆面积为,
得截面圆面积取值范围是.
故D项正确.
故选:ACD.
三 填空题:(本题共4小题,每小题5分,共20分)
若函数在区间[2,+∞)上是增函数,则实数的取值范围是 (-4,4] .
14.若,且,则
15. 已知函数,则关于的不等式的解集为______________.
【答案】
【解析】令则为上的单增奇函数,
16.设抛物线=4x的焦点为F,过F的直线l交抛物线于A,B两点,过AB的中点M作y轴的垂线与抛物线在第一象限内交于点P,若|PF|=,则直线l的方程为_____________.
17.(本小题满分10分)
在中,角,,的对边分别为,,,且.
(1)求角的大小;
(2)已知外接圆半径,且,求的周长.
【答案】(1);(2).
【解析】(1),,
即,,
又,.……………………………………………………………………………………….5分
(2),,,∴由余弦定理可得,,
∴,∵,所以得,∴周长.…………………………………………10分
18.(本小题满分12分)
已知数列是等差数列,,,数列的前项和为,且.
(Ⅰ)求数列、的通项公式;
(Ⅱ)记,若数列的前项和为,证明:.
【答案】见解析
【解析】(1)由已知得,解得,所以…………………………2分
当时,, (1)…………………………………………3分
,当时, (2)………………………5分
由(1),(2)得…………………………………………………………………6分
(Ⅱ)由(Ⅰ)知,所以………………………………………………8分
………………………………………………………10分
…………………………………………………………………………………………11分
…………………………………………………………………………………12分
19.某机构组织语文、数学学科能力竞赛,每个考生都参加两科考试,按照一定比例淘汰后,按学科分别评出一二三等奖.现有某考场的两科考试数据统计如下,其中数学科目成绩为二等奖的考生有人.
(1)求该考场考生中语文成绩为一等奖的人数;
(2)用随机抽样的方法从获得数学和语文二等奖的考生中各抽取人,进行综合素质测试,将他们的综合得分绘成茎叶图(如图),求两类样本的平均数及方差并进行比较分析;
(3)已知该考场的所有考生中,恰有人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取人进行访谈,求两人两科成绩均为一等奖的概率.
19.【答案】(Ⅰ)由数学成绩为二等奖的考生有人,可得,所以语文成绩为一等奖的考生人............2分
(Ⅱ)设数学和语文两科的平均数和方差分别为,,,
,
,因为,,所以数学二等奖考生较语文二等奖考生综合测试平均分高,但是稳定性较差. ..............7分
(Ⅲ)两科均为一等奖共有人,仅数学一等奖有人,仅语文一等奖有人----9分
设两科成绩都是一等奖的人分别为,只有数学一科为一等奖的人分别是,只有语文一科为一等奖的人是,则随机抽取两人的基本事件空间为 ,共有个,而两人两科成绩均为一等奖的基本事件共个,所以两人的两科成绩均为一等奖的概率. .................12分
20. (满分12分)已知椭圆C:(a>b>0),点P(1,)在椭圆上,且离心率e=.
(1)求椭圆C的方程;
(2)若椭圆C的右焦点为F,过B(4,0)的直线l与椭圆C交于D,E两点,求证:直线FD与直线FE斜率之和为定值.
(1)由题意知,所以a=2c,-=
故椭圆的方程为,
又点P(1,)在椭圆上,代入解得
所以=4,
故椭圆C的方程为.
(2)证明:设直线l的方程为y=k(x-4),D(x1,y1),E(x2,y2),
联立方程组,可得
(3+4k2)x2-32k2x+64k2-12=0,
则,解得<
∴x1+ x2=,x1 x2=,
所以直线FD与直线FE斜率之和为0.
21.如图,在三棱柱ABC-A1B1C1中,四边形A1C1CA为菱形,∠B1A1A=∠C1A1A=60°,AC=4,AB=2,平面ACC1A1⊥平面ABB1A1,Q在线段AC上移动,P为棱AA1的中点.
(1)若Q为线段AC的中点,H为BQ中点,延长AH交BC于D,求证:AD∥平面B1PQ;
(2)若二面角B1-PQ-C1的平面角的余弦值为,求点P到平面BQB1的距离.
(1)证明 如图,取BB1中点E,连接AE,EH.
∵H为BQ中点,∴EH∥B1Q.
在平行四边形AA1B1B中,P,E分别为AA1,BB1的中点,∴AE∥PB1.
又EH∩AE=E,PB1∩B1Q=B1,
∴平面EHA∥平面B1QP.
∵AD 平面EHA,∴AD∥平面B1PQ............................5分
(2)解 连接PC1,AC1,
∵四边形A1C1CA为菱形,
∴AA1=AC=A1C1=4.
又∠C1A1A=60°,
∴△AC1A1为正三角形.
∵P为AA1的中点,∴PC1⊥AA1.
∵平面ACC1A1⊥平面ABB1A1,平面ACC1A1∩平面ABB1A1=AA1,PC1 平面ACC1A1,∴PC1⊥平面ABB1A1,在平面ABB1A1内过点P作PR⊥AA1交BB1于点R.建立如图所示的空间直角坐标系P-xyz,则P(0,0,0),A1(0,2,0),A(0,-2,0),C1(0,0,2),C(0,-4,2),............................7分
设=λ=λ(0,-2,2),λ∈[0,1],
∴Q(0,-2(λ+1),2λ),
∴=(0,-2(λ+1),2λ).
∵A1B1=AB=2,∠B1A1A=60°,
∴B1(,1,0),∴=(,1,0).
设平面PQB1的法向量为m=(x,y,z),
则
得
令x=1,则y=-,z=-,
∴平面PQB1的一个法向量为m=1,-,-,
设平面AA1C1C的法向量为n=(1,0,0),二面角B1-PQ-C1的平面角为θ,则cos θ===.∴λ=或λ=-(舍),......................10分
∴=,∴Q(0,-3,).
又B(,-3,0),∴=(,0,-),∴||==.
连接BP,设点P到平面BQB1的距离为h,则××4××=××4××h,
∴h=,即点P到平面BQB1的距离为....................12分
22.已知函数f(x)=aln x-ax-3(a∈R).
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2·在区间(t,3)上总不是单调函数,求m的取值范围.
[解析] (1)函数f(x)的定义域为(0,+∞),且f′(x)=.
当a>0时,f(x)的增区间为(0,1),减区间为(1,+∞);
当a<0时,f(x)的增区间为(1,+∞),减区间为(0,1);
当a=0时,f(x)不是单调函数.................................5分
(2)由(1)及题意得f′(2)=-=1,即a=-2,
∴f(x)=-2ln x+2x-3,f′(x)=.
∴g(x)=x3+x2-2x,∴g′(x)=3x2+(m+4)x-2.
∵g(x)在区间(t,3)上总不是单调函数,
即g′(x)=0在区间(t,3)上有变号零点.由于g′(0)=-2,
∴
当g′(t)<0,即3t2+(m+4)t-2<0对任意t∈[1,2]恒成立,由于g′(0)<0,故只要g′(1)<0且g′(2)<0,即m<-5且m<-9,即m<-9;
由g′(3)>0,即m>-.
所以-<m<-9.
即实数m的取值范围是...................12分
同课章节目录
