2.双曲线的简单几何性质(2)
文档属性
| 名称 | 2.双曲线的简单几何性质(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 494.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-08 00:00:00 | ||
图片预览




文档简介
课件12张PPT。双曲线的简单几何性质
(二)双曲线的简单几何性质
(二)我们的目标:2、掌握共渐近线的双曲线系方程
及其应用。1、巩固双曲线的几何性质。3 、解决直线被双曲线所截得的
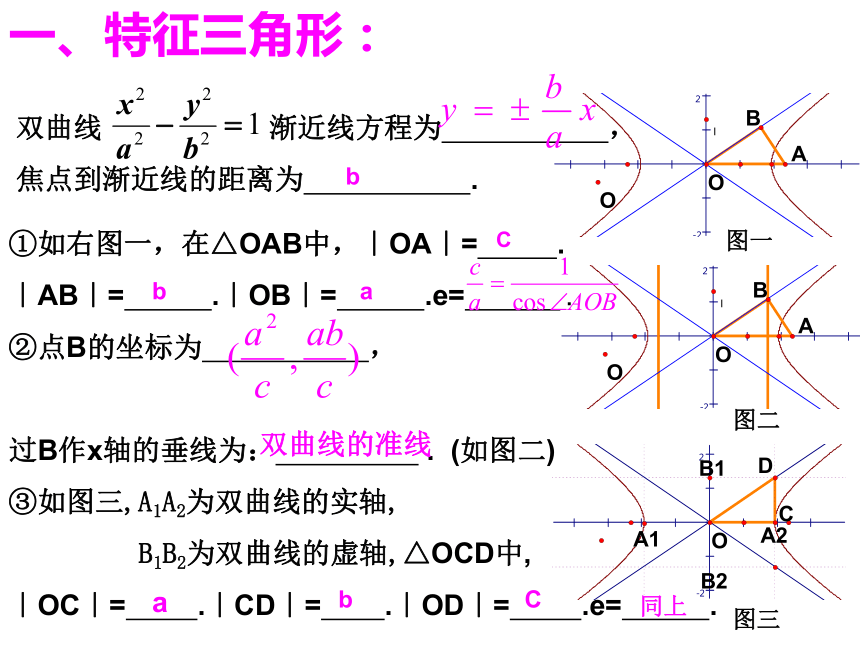
弦长问题。一、特征三角形:双曲线 渐近线方程为 ,
焦点到渐近线的距离为 .①如右图一,在△OAB中,|OA|= .
|AB|= .|OB|= .e= .
②点B的坐标为 ,
过B作x轴的垂线为: . (如图二)
③如图三,A1A2为双曲线的实轴,
B1B2为双曲线的虚轴,△OCD中,
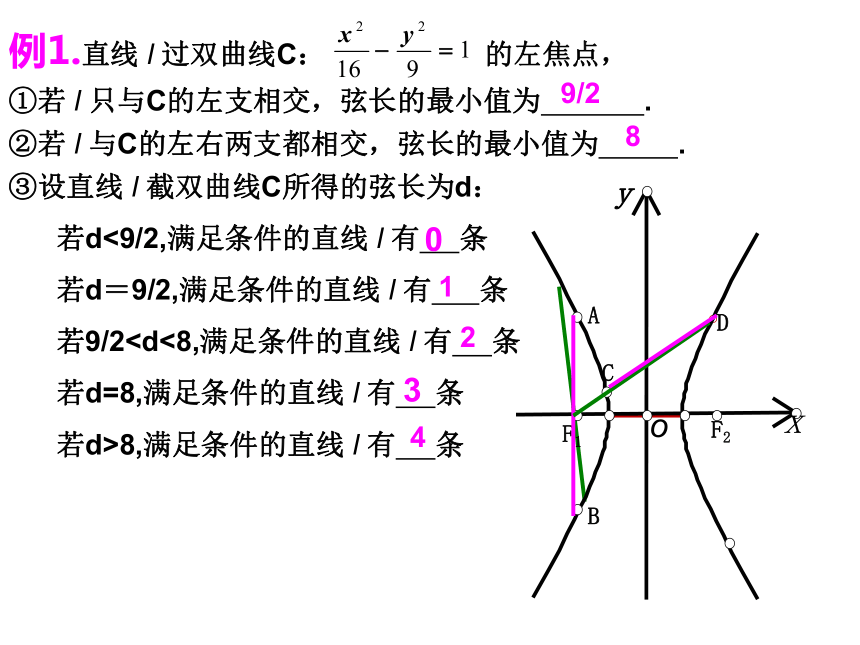
|OC|= .|CD|= .|OD|= .e= .图一图二图三bCba双曲线的准线abC同上通径:与实轴垂直的焦点弦。焦点弦:过双曲线一个焦点的直线截双曲线所得的线段。焦半径:双曲线上的点到焦点的线段(焦半径公式)。请指出右图中的焦半径,焦点弦和通径.二、弦长中的最值问题:例1.直线 l 过双曲线C: 的左焦点,①若 l 只与C的左支相交,弦长的最小值为 .②若 l 与C的左右两支都相交,弦长的最小值为 .③设直线 l 截双曲线C所得的弦长为d:
若d<9/2,满足条件的直线 l 有 条
若d=9/2,满足条件的直线 l 有 条
若9/2 若d=8,满足条件的直线 l 有 条
若d>8,满足条件的直线 l 有 条9/2801234y过双曲线C 的右焦点F2作直线 l :
(1)若 l 只与C的右支相交,
①所得的弦长中通径最短(试证明),通径长为 。②截得的弦长大于通径的直线 l 有 条。
③截得的弦长小于通径的直线 l 有 条。(2)若 l 与C的左右两支都相交,
①所得的弦长中实轴最短(试证明),为 。②截得的弦长大于2a的直线 l 有 条。
③截得的弦长小于2a的直线 l 有 条。练习:过双曲线 的右焦点作直线 l ,交双曲线于A,B两点,若┃AB┃=5,则这样的直线 l 有 条。202a204λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线一般地,已知渐近线及双曲线上一点,求双曲线的方程,只有唯一解。三.关于共渐近线的
双曲线系问题:注:“共渐近线”的双曲线的应用。λ>0表示焦点在x轴上的双曲线;λ<0表示焦点在y轴上的双曲线√小结:1.用弦长公式计算时与椭圆是一样的
2.过焦点的弦用定义计算时是有差异的:(若弦过F1)
如果弦端点A,B在不同支上,则有|AB|=┃|BF1|-|AF1|┃
如果弦端点A,B在同一支上,则有|AB|=|BF1|+|AF1|
(若弦过F2时,也可类似处理)四、弦长及焦三角形面积的计算例2.经过双曲线 的左焦点F1,作倾斜角为 的弦AB.
(1)求|AB|;
(2)求△F2AB的周长l(其中F2为双曲线的右焦点。)
(3)求△F2AB的面积S.变式一:经过双曲线 的左焦F1,作倾斜角为 的弦AB.
(1)求|AB|;
(2)求△F2AB的周长L(其中F2为双曲线的右焦点。)
(3)求△F2AB的面积S.(与椭圆大同小异 )333例3: 给定椭圆 ,求和这椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,求出相应四边形各顶点的坐标。 解:已知椭圆为 ,焦点F1(0,2), F2(0,-2), 其面积,由 课后小结:1、双曲线的2个特征三角形
2、几何法作双曲线的准线
3、过焦点的直线交双曲线所得的弦长中:
1)若直线只和双曲线的一支相交,通径最短
2)若直线和双曲线的两支都相交,实轴最短4、弦长的求法:
1)用弦长公式计算时与椭圆是一样的
2)过焦点的弦用定义计算时和椭圆是有差异的:(若弦过F1)
如果弦端点A,B在不同支上,则有|AB|=┃|BF1|-|AF1|┃
如果弦端点A,B在同一支上,则有|AB|=|BF1|+|AF1|
(若弦过F2时,也可类似处理)作业: 1.纠错.2.复习总结整理.3.完成综合试卷
(二)双曲线的简单几何性质
(二)我们的目标:2、掌握共渐近线的双曲线系方程
及其应用。1、巩固双曲线的几何性质。3 、解决直线被双曲线所截得的
弦长问题。一、特征三角形:双曲线 渐近线方程为 ,
焦点到渐近线的距离为 .①如右图一,在△OAB中,|OA|= .
|AB|= .|OB|= .e= .
②点B的坐标为 ,
过B作x轴的垂线为: . (如图二)
③如图三,A1A2为双曲线的实轴,
B1B2为双曲线的虚轴,△OCD中,
|OC|= .|CD|= .|OD|= .e= .图一图二图三bCba双曲线的准线abC同上通径:与实轴垂直的焦点弦。焦点弦:过双曲线一个焦点的直线截双曲线所得的线段。焦半径:双曲线上的点到焦点的线段(焦半径公式)。请指出右图中的焦半径,焦点弦和通径.二、弦长中的最值问题:例1.直线 l 过双曲线C: 的左焦点,①若 l 只与C的左支相交,弦长的最小值为 .②若 l 与C的左右两支都相交,弦长的最小值为 .③设直线 l 截双曲线C所得的弦长为d:
若d<9/2,满足条件的直线 l 有 条
若d=9/2,满足条件的直线 l 有 条
若9/2
若d>8,满足条件的直线 l 有 条9/2801234y过双曲线C 的右焦点F2作直线 l :
(1)若 l 只与C的右支相交,
①所得的弦长中通径最短(试证明),通径长为 。②截得的弦长大于通径的直线 l 有 条。
③截得的弦长小于通径的直线 l 有 条。(2)若 l 与C的左右两支都相交,
①所得的弦长中实轴最短(试证明),为 。②截得的弦长大于2a的直线 l 有 条。
③截得的弦长小于2a的直线 l 有 条。练习:过双曲线 的右焦点作直线 l ,交双曲线于A,B两点,若┃AB┃=5,则这样的直线 l 有 条。202a204λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线一般地,已知渐近线及双曲线上一点,求双曲线的方程,只有唯一解。三.关于共渐近线的
双曲线系问题:注:“共渐近线”的双曲线的应用。λ>0表示焦点在x轴上的双曲线;λ<0表示焦点在y轴上的双曲线√小结:1.用弦长公式计算时与椭圆是一样的
2.过焦点的弦用定义计算时是有差异的:(若弦过F1)
如果弦端点A,B在不同支上,则有|AB|=┃|BF1|-|AF1|┃
如果弦端点A,B在同一支上,则有|AB|=|BF1|+|AF1|
(若弦过F2时,也可类似处理)四、弦长及焦三角形面积的计算例2.经过双曲线 的左焦点F1,作倾斜角为 的弦AB.
(1)求|AB|;
(2)求△F2AB的周长l(其中F2为双曲线的右焦点。)
(3)求△F2AB的面积S.变式一:经过双曲线 的左焦F1,作倾斜角为 的弦AB.
(1)求|AB|;
(2)求△F2AB的周长L(其中F2为双曲线的右焦点。)
(3)求△F2AB的面积S.(与椭圆大同小异 )333例3: 给定椭圆 ,求和这椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,求出相应四边形各顶点的坐标。 解:已知椭圆为 ,焦点F1(0,2), F2(0,-2), 其面积,由 课后小结:1、双曲线的2个特征三角形
2、几何法作双曲线的准线
3、过焦点的直线交双曲线所得的弦长中:
1)若直线只和双曲线的一支相交,通径最短
2)若直线和双曲线的两支都相交,实轴最短4、弦长的求法:
1)用弦长公式计算时与椭圆是一样的
2)过焦点的弦用定义计算时和椭圆是有差异的:(若弦过F1)
如果弦端点A,B在不同支上,则有|AB|=┃|BF1|-|AF1|┃
如果弦端点A,B在同一支上,则有|AB|=|BF1|+|AF1|
(若弦过F2时,也可类似处理)作业: 1.纠错.2.复习总结整理.3.完成综合试卷
