人教版九年级数学下册第27章相似同步测试(word解析版)
文档属性
| 名称 | 人教版九年级数学下册第27章相似同步测试(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 625.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 08:26:54 | ||
图片预览



文档简介
人教版九年级数学下册 第27章《相似》同步测试
一、单选题
1.已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD = 30°,AC⊥BC,AB =" 8" cm,则△COD的面积为( ).A.cm2 B.cm2 C.cm2 D.cm2
2.如图,在平面直角坐标系中,点、的坐标分别为(-4,4)、(0,4),点、的坐标分别为(0,1)、(2,1).若线段和是位似图形,且位似中心在轴上,则位似中心的坐标为( )
A.. B.. C.. D..
3.如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=3,AB=4,则四边形AEDF的周长为( )
A.8 B.9 C.10 D.11
4.如图,点在射线上,点在射线上,且,.若,的面积分别为1,4,则图中三个阴影三角形面积之和为 ( )
A.8 B.9 C.10 D.10.5
5.如图,在平面直角坐标系中,的顶点、的坐标分别为、,,,函数的图象经过点,则的值为( )
A.2 B.4 C.8 D.10
6.如图,中,,以AB上一点О为圆心作,分别切AC、BC于E、D,,,则的半径长为( )
A.5 B. C. D.
7.已知△ABC∽△A B C ,且△ABC与△A B C 的周长比为,则△ABC与△A B C 的面积比为( )
A. B. C. D.
8.1米长的标杆直立在水平的地面上,它在阳光下的影长为0.8米;在同一时刻,若某电视塔的影长为100米,则此电视塔的高度应是( )
A.80米 B.85米 C.120米 D.125米
9.已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )
A.1:4 B.4:1 C.1:2 D.2:1
10.如图,把一张纸片沿着对折,使点落在的外部点处,若,,则的度数是( )
A. B. C. D.
11.△ABC是等腰三角形,AB=AC,∠A=30°,△ABC∽△A′B′C′,则∠C′=( )
A.30° B.60° C.50° D.75°
二、填空题
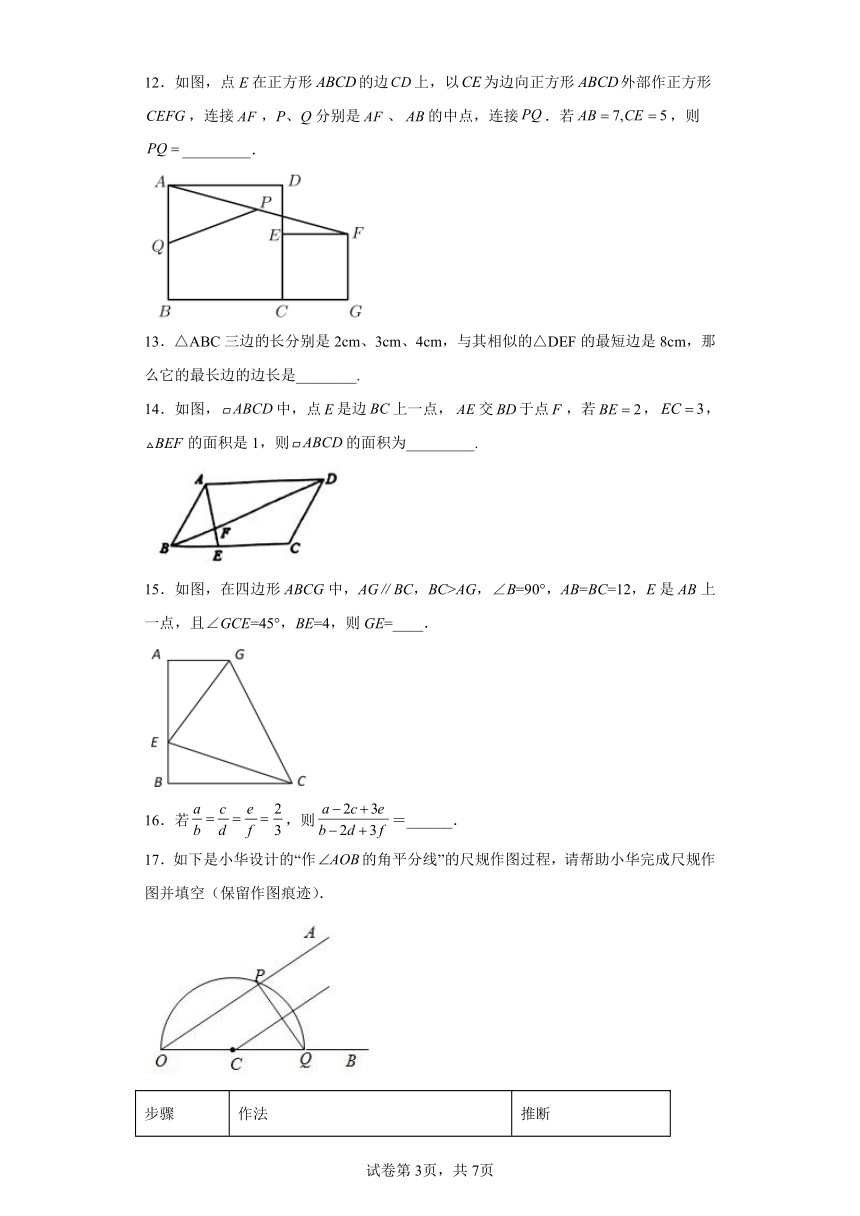
12.如图,点E在正方形的边上,以为边向正方形外部作正方形,连接,P、Q分别是、的中点,连接.若,则_________.
13.△ABC三边的长分别是2cm、3cm、4cm,与其相似的△DEF的最短边是8cm,那么它的最长边的边长是________.
14.如图,中,点是边上一点,交于点,若,,的面积是1,则的面积为_________.
15.如图,在四边形ABCG中,AG∥BC,BC>AG,∠B=90°,AB=BC=12,E是AB上一点,且∠GCE=45°,BE=4,则GE=____.
16.若,则=______.
17.如下是小华设计的“作的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).
步骤 作法 推断
第一步 在上任取一点C,以点C为圆心,为半径作半圆,分别交射线于点P,点Q,连接 ① ,理由是 ②
第二步 过点C作的垂线,交于点D,交于点E , ③
第三步 作射线 射线平分
射线为所求作.
18.如果两个相似三角形的面积比是1:9,那么这两个三角形的相似比是______.
19.已知,则的值为_________.
20. 若在比例尺为的地图上,测得两地的距离为5cm,则这两地的实际距离是_____km
21.如图,AG∥BC,如果AF:FB=3:5,BC:CD=3:2,那么AE:EC=_____.
22.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DE=8cm,DF=10cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=________m.
三、解答题
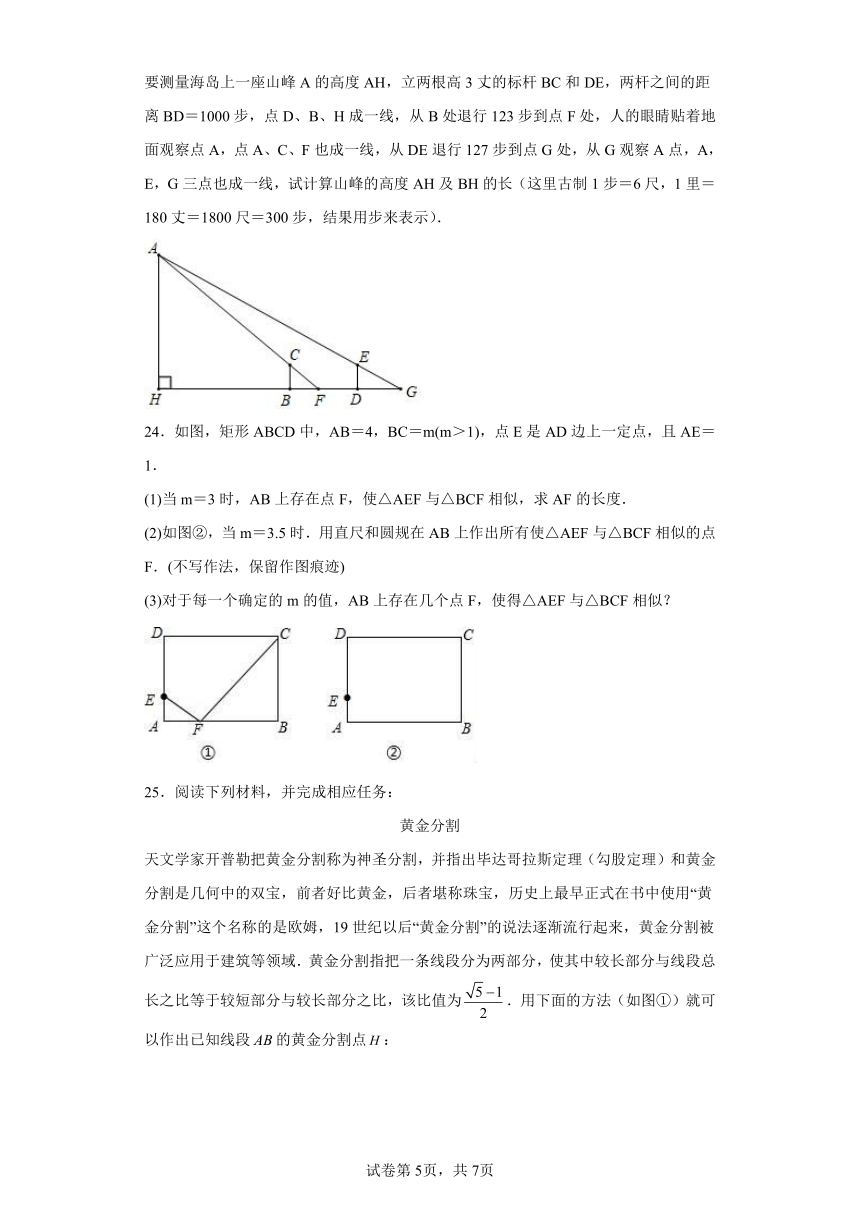
23.刘徽,公元3世纪人,是中国历史上最杰出的数学家之一.《九章算术注》和《海岛算经》是他留给后世最宝贵的数学遗产.《海岛算经》第一个问题的大意是:如图,要测量海岛上一座山峰A的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从DE退行127步到点G处,从G观察A点,A,E,G三点也成一线,试计算山峰的高度AH及BH的长(这里古制1步=6尺,1里=180丈=1800尺=300步,结果用步来表示).
24.如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)
(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
25.阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为.用下面的方法(如图①)就可以作出已知线段的黄金分割点:
①以线段为边作正方形,
②取的中点,连接,
③延长到,使,
④以线段为边作正方形,点就是线段的黄金分割点.
以下是证明点就是线段的黄金分割点的部分过程:
证明:设正方形的边长为1,则,
为中点,
,
在中,,
,
,
,
…
任务:
(1)补全题中的证明过程;
(2)如图②,点为线段的黄金分割点,分别以为边在线段同侧作正方形和矩形,连接.求证:;
(3)如图③,在正五边形中,对角线与分别交于点求证:点是的黄金分割点.
26.如图,是的边上一点,,点、、分别是、、的中点,设,.
(1)试用、的线形组合表示;
(2)在图中画出在、方向上的分向量.
27.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【详解】
解:∵梯形ABCD是等腰梯形,CD∥AB,
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2-BC2,
∴AC=4cm,
∵梯形ABCD是等腰梯形,
∴AC=BD=4cm,
∴S△ABC=×4×4=8cm,
设DO为x,则CO=x,则AO=BO=(4-x)cm,
在Rt△COB中,CO2+BC2=BO2,
即:x2+42=(4-x)2
∴D0=cm,
∴S△ADO=××4=,
∴S△AOB=S△ABC-S△ADO=
∵AB∥CD,
∴△AOB∽△DOC,
∴()2=
∴S△DOC=,故选A
2.B
【解析】
【分析】
直接利用位似图形的性质、结合相似三角形的性质得出位似中心即可.
【详解】
解:如图所示:连接AD,交y轴于点E,
∵点A、B的坐标分别为(-4,4)、(0,4),点C、D的坐标分别为(0,1)、(2,1);
∴AB=4,CD=2,BC=3,AB∥DC,
∴△ABE∽△DCE,
,
,
∴2=,
解得:EC=1,
则E点坐标为:(0,2),
故位似中心的坐标为:(0,2).
故选:B.
【点睛】
此题主要考查了位似变换以及相似三角形的性质,正确运用相似三角形的性质是解题关键.
3.A
【解析】
【分析】
根据勾股定理先求出BC的长,再根据三角形中位线定理和直角三角形的性质求出DE和AE的长,进而由已知可判定四边形AEDF是平行四边形,从而求得其周长.
【详解】
解:在Rt△ABC中,∵AC=3,AB=4,
∴BC=5,
∵E是BC的中点,
∴AE=BE=2.5,
∴∠BAE=∠B,
∵∠FDA=∠B,
∴∠FDA=∠BAE,
∴DF∥AE,
∵D、E分别是AB、BC的中点,
∴DE∥AC,DE=AC=1.5,
∴四边形AEDF是平行四边形,
∴四边形AEDF的周长=2×(1.5+2.5)=8.
故选:A.
【点睛】
本题主要考查了直角三角形的性质、等腰三角形的判定以及平行四边形的判定.熟练运用三角形的中位线定理和直角三角形的勾股定理是解题的关键.
4.D
【解析】
【分析】
由题意得,设 之间的距离为h,则由题意可得 ,再由可得 ,从而得到问题的解答.
【详解】
解:由已知得:,
∴,
设之间的距离为h,则: ,
,
,
同理有,
∴图中三个阴影三角形面积之和为:
,
故选D.
【点睛】
本题考查三角形相似的综合应用,熟练掌握三角形相似的判定与性质是解题关键.
5.D
【解析】
【分析】
过点B作BD⊥x轴,垂足为D,根据A、C的坐标分别是(0,2)、(4,0)可知OA=2,OC=4,然后证明△AOC∽△CDB,利用相似三角形的性质求出CD=1,DB=2,得到点B的坐标,再求出k的值即可.
【详解】
解:过点B作BD⊥x轴,垂足为D,
∵A、C的坐标分别是(0,2)、(4、0),
∴OA=2,OC=4,
∵∠ACB=90°,
∴∠OAC+∠OCA=∠OCA+∠BCD=90°,
∴∠OAC=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△CDB,
∴,即,
∴CD=1,DB=2,
∴OD=4+1=5,即B(5,2),
把B(5,2)代入得:k=5×2=10,
故选:D.
【点睛】
本题考查了坐标与图形,相似三角形的判定和性质以及反比例函数图象上点的坐标特征,正确的作出辅助线,恰当的将线段的长与坐标互相转化是解题的关键.
6.D
【解析】
【分析】
连接OD、OE,先设OE=x,再证明四边形ODCE是矩形,证明△AOD∽△OBE,再由比例式得出OE的长即可.
【详解】
解:连接OD、OE,
设OE=x,
∵半圆分别与AC、BC相切,
∴∠CDO=∠CEO=90°,
∵∠C=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴OD=CE=OE=CD=x,
∵OE∥BC,
∴△AOE∽△ABC,
∴,
∴,
解得x=,
故选:D.
【点睛】
本题考查了切线的性质.相似三角形的性质与判定,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形,证明三角形相似解决有关问题.
7.C
【解析】
【分析】
根据相似三角形的周长比等于相似比,面积比等于相似比的平方,即可求出面积比.
【详解】
∵△ABC∽△A B C ,且△ABC与△A B C 的周长比为
∴△ABC与△A B C 的相似比为
∴△ABC与△A B C 的面积比为
故选C.
【点睛】
此题考查的是相似三角形的性质,掌握相似三角形的周长比等于相似比,面积比等于相似比的平方是解决此题的关键.
8.D
【解析】
【详解】
在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
解:设电视塔的高度应是x,根据题意得:=,
解得:x=125米.
故选D.
命题立意:考查利用所学知识解决实际问题的能力.
9.A
【解析】
【详解】
∵△ABC∽△DEF,且相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故选A.
10.C
【解析】
【分析】
由折叠的性质可得出,结合平角等于180°即可求出∠CDE和∠CED的度数,再在△CDE中,利用三角形内角和定理可求出∠C的度数.
【详解】
由折叠的性质可得出,,
,
,
在中,,
,
故选:C
【点睛】
本题考查了三角形内角和定理、折叠的性质以及补角,利用折叠的性质及平角等于180°,求出∠CDE和∠CED的度数是解题的关键.
11.D
【解析】
【分析】
利用相似三角形的对应角相等即可得到答案.
【详解】
∵△ABC是等腰三角形,AB=AC,∠A=30°,∴∠C=(180°﹣∠A)÷2=75°.
∵△ABC∽△A′B′C′,∴∠C′=∠C=75°.
故选D.
【点睛】
本题考查了等腰三角形的性质及相似三角形的性质,解题的关键是利用等腰三角形的性质求得等腰三角形底角的度数.
12.
【解析】
【分析】
连接BF,根据正方形的性质和勾股定理求出BF,再根据中位线定理求解即可.
【详解】
解:如图,连接BF,
∵正方形ABCD和正方形CEFG中,,,
∴,,
∴,
∴
∴,
∵、为AB,AF中点,
∴,
故答案为:.
【点睛】
本题考查了正方形的性质,勾股定理,中位线定理,解题的关键是求出BF的长.
13.16cm
【解析】
【分析】
由三角形相似可得对应边分别成比例.
【详解】
解:设△DEF的最长边长x,则由题意得:
,解得x=16,
故答案为:16.
【点睛】
本题考察了相似比的定义.
14.
【解析】
【分析】
利用△BFE∽△DFA,可求出△DFA的面积,再利用来求出△BAF的面积,即可得△ABD的面积,它的2倍即为的面积.
【详解】
解:中,BE∥AD,
∴△BFE∽△DFA,
∴.
而△BEF的面积是1,
∴S△DFA=.
又∵△BFE∽△DFA
∴.
∵,即可知S△BAF=.
而S△ABD=S△BAF+S△DFA
∴S△AFD=.
∴ ABCD的面积=×2=.
故答案为.
【点睛】
本题考查的是利用相似形的性质求面积,把握相似三角形的面积比等于相似比的平方是解决本题的重点.
15.10
【解析】
【分析】
如图(见解析),先根据等腰直角三角形的判定与性质可得,再根据平行线的性质可得,从而可得,然后根据相似三角形的判定与性质可得,设,利用线段的和差可求出x的值,最后利用勾股定理可求出AG的长,由此在中,利用勾股定理即可得.
【详解】
如图,连接AC,过点G作于点D
,
是等腰直角三角形
在和中,
,即
设,则,
解得
又
则在中,由勾股定理得:
故答案为:10.
【点睛】
本题考查了平行线的性质、等腰直角三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识点,通过作辅助线,构造相似三角形是解题关键.
16.
【解析】
【分析】
根据可得,把a,c,e代入所求代数式中,约分后即可求得结果.
【详解】
∵
∴
∴
故答案为:
【点睛】
本题考查了比例的性质,求代数式的值,根据比例的性质变形是关键.
17.见解析;①90;②直径所对的圆周角是直角;③
【解析】
【分析】
根据直径所对的圆周角是直角,和同弧所对的圆周角相等即可得出结论
【详解】
解:补全的图形如图1所示.
①∵OQ是直径
∴∠OPQ=90°
故答案为:90;
②故答案为:直径所对的圆周角是直角;
③∵CE⊥PQ
∴由垂径定理得:.
故答案为:
【点睛】
本题考查圆周角定理的推论,垂径定理,熟练掌握圆周角定理及推论是关键
18.1:3
【解析】
【分析】
由两个相似三角形的面积比是1:9,根据相似三角形的面积比等于相似比的平方,即可求得答案.
【详解】
解:∵两个相似三角形的面积比是1:9,
∴这两个三角形的相似比是:1:3.
故答案为1:3.
【点睛】
本题考查了相似三角形的性质.此题比较简单,注意掌握定理的应用是解此题的关键.
19.
【解析】
【分析】
根据比例的性质,可用b表示a,根据分式的性质,即可得到答案.
【详解】
解:∵
∴
∴
故答案为:.
【点睛】
本题考查了比例的性质,利用比例的性质得出是解题关键,又利用了分式的性质.
20.50
【解析】
【详解】
5×1000000=5000000(cm)
=50km
21.3:2;
【解析】
【分析】
由AG//BC可得△AFG与△BFD相似 ,△AEG与△CED相似,根据相似比求解.
【详解】
假设:AF=3x,BF=5x ,
∵△AFG与△BFD相似
∴AG=3y,BD=5y
由题意BC:CD=3:2则CD=2y
∵△AEG与△CED相似
∴AE:EC= AG:DC=3:2.
【点睛】
本题考查的是相似三角形,熟练掌握相似三角形的性质是解题的关键.
22.7.5
【解析】
【分析】
利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小颖同学的身高即可求得树高AB.
【详解】
解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴,
∵DE=8cm=0.08m,DF=10cm=0.1m,AC=1.5m,CD=8m,
∴由勾股定理求得EF=0.06m,
∴,
∴BC=6米,
∴AB=AC+BC=1.5+6=7.5(米).
故答案为:7.5.
【点睛】
本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形的模型.
23.AH为1255步,HB为30750步
【解析】
【分析】
根据题意得出△FCB∽△FAH,△EDG∽△AHG,进而利用相似三角形的性质求出即可.
【详解】
解:由题意,得,AH⊥HG,CB⊥HG,
∴∠AHF=90°,∠CBF=90°,
∴∠AHF=∠CBF,
∵∠AFB=∠CFB,
∴△CBF∽△AHF,
∴
同理可得
∵BF=123,BD=1000,DG=127,
∴HF=HB+123,HG=HB+1000+127=HB+1127,BC=DE=3丈=3×=5步,
∴
解得HB=30750,HA=1255步,
答:AH为1255步,HB为30750步.
【点睛】
本题考查了相似三角形的应用,解题的关键是掌握相似三角形的判定和性质.
24.(1)AF=1或3;(2)见解析;(3)见解析.
【解析】
【详解】
试题分析:
(1)由题意可知,∠A=∠B=90°,由此可知要使△AEF与△BCF相似,存在两种情况:①当∠AEF=∠BFC时,若,则两三角形相似;②当∠AEF=∠BCF时, 若,则两三角形相似;由这两种情况分别根据已知条件进行计算即可得到相应的AF的值;
(2)如下图所示:①延长DA到E′,使AE′=AE,连接CE′交AB于点F1;②连接CE,以CE为直径作圆,分别交AB于点F2、F3;则F1、F2、F3为所求点;
(3)结合(1)(2)可知,当m=3时,符合条件的点F有2个,当m=4时,符合条件的点F也有2个,而当14时,以CE为直径的圆和AB相离,此时符合条件的点F只有1个.
试题解析:
(1)①当∠AEF=∠BFC时,
要使△AEF∽△BFC,需,即,
解得AF=1或3;
②当∠AEF=∠BCF时,
要使△AEF∽△BCF,需=,即,
解得AF=1;
综上所述AF=1或3
(2)如下图所示,图中F1、F2、F3为所求点;
(提示:延长DA,作点E关于AB的对称点E′,连结CE′,交AB于点F1;连结CE,以CE为直径作圆交AB于点F2、F3);
(3)如(2)中所作图形,
当m=4时,由已知条件可得DE=3,则CE=5,即图中圆的直径为5,由梯形中位线定理可得此时图中所作圆的圆心到AB的距离=2.5=所作圆的半径,F2和F3重合,即当m=4时,符合条件的F有2个;
当m>4时,图中所作圆和AB相离,此时F2和F3不存在了,即此时符合条件的F只有F11个;
而当1<m<4且m≠3时,由所作图形可知,符合条件的F有3个;
综上所述:可得:①当1<m<4且m≠3时,符合条件的F有3个; ②当m=3时,符合条件的F有2个;③当m=4时,符合条件的F有2个;④当m>4时,符合条件的F有1个.
25.(1)详见解析;(2)详见解析;(3)详见解析
【解析】
【分析】
(1)设正方形ABCD的边长为1,则AB=AD=1,由勾股定理得出,得出,求出,由正方形的性质得出,求出,即可得出结论;
(2)由正方形和矩形的性质得出∠EAB=∠BCD=90°,AC=CD=AE=DE=BF,BC=DF,由点C为线段AB的黄金分割点,得出,因此,即可得出结论;
(3)根据正五边形的性质得到∠DAE=∠DAE,∠ADE=∠AEM=36°,推出△AME∽△AED,根据相似三角形的性质得到∴AE:AD=AM:AE,得到AE2=AD AM,等量代换即可得到结论.
【详解】
(1)证明:设正方形ABCD的边长为1,则AB=AD=1,
∵E为AD中点,
∴AE=,
∴在Rt△BAE中,
∵EF=BE
∴
∴,
∵四边形AFGH是正方形,
∴,
∴,
∴点H是线段AB的黄金分割点;
(2)证明:∵四边形ACDE是正方形,四边形CBFD是矩形,
∴∠EAB=∠BCD=90°,AC=CD=AE=DE=BF,BC=DF,
∵点C为线段AB的黄金分割点,
∴,
∴,
∴△EAB∽△BCD;
(3)证明:∵五边形ABCDE是正五边形,
∴∠BAE=∠AED=(5-2)×180°=108°,AB=AE=DE,
∴∠ABE=∠AEM=∠DAE=∠ADE=(180°-108°)=36°,
∵∠DAE=∠DAE,∠ADE=∠AEM=36°,
∴△AME∽△AED,
∴AE:AD=AM:AE,
∴AE2=AD AM,
∵AE=DE=DM,
∴DM2=AD AM,
∴点M是AD的黄金分割点.
【点睛】
本题是相似形综合题目,考查了相似三角形的判定与性质、黄金分割、正方形的性质、矩形的性质、正五边形的性质、勾股定理、等腰三角形的性质等知识;本题综合性强,熟练掌握黄金分割和正方形的性质以及正五边形的性质,证明三角形相似是解题的关键.
26.(1);(2)图见解析.
【解析】
【分析】
(1)利用三角形的中位线定理以及三角形法则解答即可;
(2)利用平行四边形的法则作图即可.
【详解】
解:(1)∵AE=ED,BF=DF,
∴EF∥AB,EF=AB,
∴=,
∵BF=DF,BG=GC,
∴FG∥CD,FG=DC=AC,
∴=,
∵=+,
∴.
(2)如图所示,图中,即为所求.
【点睛】
本题考查了三角形的中位线定理、三角形法则、平行四边形法则以及常见作图等知识,熟练掌握以上基本知识是解题的关键.
27.(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.
【解析】
【详解】
试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;
(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.
试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
,
∴△AGE≌△AFE(SAS);
(2)设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.
则△ADF≌△ABG,DF=BG.
由(1)知△AEG≌△AEF,
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NF=DF,
∴a﹣BE=a﹣DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MG=BM=DF=NF,
∴EF2=ME2+NF2;
(3)EF2=2BE2+2DF2.
如图所示,延长EF交AB延长线于M点,交AD延长线于N点,
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.
由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM﹣GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,
即2(DF2+BE2)=EF2
考点:四边形综合题
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD = 30°,AC⊥BC,AB =" 8" cm,则△COD的面积为( ).A.cm2 B.cm2 C.cm2 D.cm2
2.如图,在平面直角坐标系中,点、的坐标分别为(-4,4)、(0,4),点、的坐标分别为(0,1)、(2,1).若线段和是位似图形,且位似中心在轴上,则位似中心的坐标为( )
A.. B.. C.. D..
3.如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=3,AB=4,则四边形AEDF的周长为( )
A.8 B.9 C.10 D.11
4.如图,点在射线上,点在射线上,且,.若,的面积分别为1,4,则图中三个阴影三角形面积之和为 ( )
A.8 B.9 C.10 D.10.5
5.如图,在平面直角坐标系中,的顶点、的坐标分别为、,,,函数的图象经过点,则的值为( )
A.2 B.4 C.8 D.10
6.如图,中,,以AB上一点О为圆心作,分别切AC、BC于E、D,,,则的半径长为( )
A.5 B. C. D.
7.已知△ABC∽△A B C ,且△ABC与△A B C 的周长比为,则△ABC与△A B C 的面积比为( )
A. B. C. D.
8.1米长的标杆直立在水平的地面上,它在阳光下的影长为0.8米;在同一时刻,若某电视塔的影长为100米,则此电视塔的高度应是( )
A.80米 B.85米 C.120米 D.125米
9.已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )
A.1:4 B.4:1 C.1:2 D.2:1
10.如图,把一张纸片沿着对折,使点落在的外部点处,若,,则的度数是( )
A. B. C. D.
11.△ABC是等腰三角形,AB=AC,∠A=30°,△ABC∽△A′B′C′,则∠C′=( )
A.30° B.60° C.50° D.75°
二、填空题
12.如图,点E在正方形的边上,以为边向正方形外部作正方形,连接,P、Q分别是、的中点,连接.若,则_________.
13.△ABC三边的长分别是2cm、3cm、4cm,与其相似的△DEF的最短边是8cm,那么它的最长边的边长是________.
14.如图,中,点是边上一点,交于点,若,,的面积是1,则的面积为_________.
15.如图,在四边形ABCG中,AG∥BC,BC>AG,∠B=90°,AB=BC=12,E是AB上一点,且∠GCE=45°,BE=4,则GE=____.
16.若,则=______.
17.如下是小华设计的“作的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).
步骤 作法 推断
第一步 在上任取一点C,以点C为圆心,为半径作半圆,分别交射线于点P,点Q,连接 ① ,理由是 ②
第二步 过点C作的垂线,交于点D,交于点E , ③
第三步 作射线 射线平分
射线为所求作.
18.如果两个相似三角形的面积比是1:9,那么这两个三角形的相似比是______.
19.已知,则的值为_________.
20. 若在比例尺为的地图上,测得两地的距离为5cm,则这两地的实际距离是_____km
21.如图,AG∥BC,如果AF:FB=3:5,BC:CD=3:2,那么AE:EC=_____.
22.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DE=8cm,DF=10cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=________m.
三、解答题
23.刘徽,公元3世纪人,是中国历史上最杰出的数学家之一.《九章算术注》和《海岛算经》是他留给后世最宝贵的数学遗产.《海岛算经》第一个问题的大意是:如图,要测量海岛上一座山峰A的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从DE退行127步到点G处,从G观察A点,A,E,G三点也成一线,试计算山峰的高度AH及BH的长(这里古制1步=6尺,1里=180丈=1800尺=300步,结果用步来表示).
24.如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)
(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
25.阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为.用下面的方法(如图①)就可以作出已知线段的黄金分割点:
①以线段为边作正方形,
②取的中点,连接,
③延长到,使,
④以线段为边作正方形,点就是线段的黄金分割点.
以下是证明点就是线段的黄金分割点的部分过程:
证明:设正方形的边长为1,则,
为中点,
,
在中,,
,
,
,
…
任务:
(1)补全题中的证明过程;
(2)如图②,点为线段的黄金分割点,分别以为边在线段同侧作正方形和矩形,连接.求证:;
(3)如图③,在正五边形中,对角线与分别交于点求证:点是的黄金分割点.
26.如图,是的边上一点,,点、、分别是、、的中点,设,.
(1)试用、的线形组合表示;
(2)在图中画出在、方向上的分向量.
27.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【详解】
解:∵梯形ABCD是等腰梯形,CD∥AB,
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2-BC2,
∴AC=4cm,
∵梯形ABCD是等腰梯形,
∴AC=BD=4cm,
∴S△ABC=×4×4=8cm,
设DO为x,则CO=x,则AO=BO=(4-x)cm,
在Rt△COB中,CO2+BC2=BO2,
即:x2+42=(4-x)2
∴D0=cm,
∴S△ADO=××4=,
∴S△AOB=S△ABC-S△ADO=
∵AB∥CD,
∴△AOB∽△DOC,
∴()2=
∴S△DOC=,故选A
2.B
【解析】
【分析】
直接利用位似图形的性质、结合相似三角形的性质得出位似中心即可.
【详解】
解:如图所示:连接AD,交y轴于点E,
∵点A、B的坐标分别为(-4,4)、(0,4),点C、D的坐标分别为(0,1)、(2,1);
∴AB=4,CD=2,BC=3,AB∥DC,
∴△ABE∽△DCE,
,
,
∴2=,
解得:EC=1,
则E点坐标为:(0,2),
故位似中心的坐标为:(0,2).
故选:B.
【点睛】
此题主要考查了位似变换以及相似三角形的性质,正确运用相似三角形的性质是解题关键.
3.A
【解析】
【分析】
根据勾股定理先求出BC的长,再根据三角形中位线定理和直角三角形的性质求出DE和AE的长,进而由已知可判定四边形AEDF是平行四边形,从而求得其周长.
【详解】
解:在Rt△ABC中,∵AC=3,AB=4,
∴BC=5,
∵E是BC的中点,
∴AE=BE=2.5,
∴∠BAE=∠B,
∵∠FDA=∠B,
∴∠FDA=∠BAE,
∴DF∥AE,
∵D、E分别是AB、BC的中点,
∴DE∥AC,DE=AC=1.5,
∴四边形AEDF是平行四边形,
∴四边形AEDF的周长=2×(1.5+2.5)=8.
故选:A.
【点睛】
本题主要考查了直角三角形的性质、等腰三角形的判定以及平行四边形的判定.熟练运用三角形的中位线定理和直角三角形的勾股定理是解题的关键.
4.D
【解析】
【分析】
由题意得,设 之间的距离为h,则由题意可得 ,再由可得 ,从而得到问题的解答.
【详解】
解:由已知得:,
∴,
设之间的距离为h,则: ,
,
,
同理有,
∴图中三个阴影三角形面积之和为:
,
故选D.
【点睛】
本题考查三角形相似的综合应用,熟练掌握三角形相似的判定与性质是解题关键.
5.D
【解析】
【分析】
过点B作BD⊥x轴,垂足为D,根据A、C的坐标分别是(0,2)、(4,0)可知OA=2,OC=4,然后证明△AOC∽△CDB,利用相似三角形的性质求出CD=1,DB=2,得到点B的坐标,再求出k的值即可.
【详解】
解:过点B作BD⊥x轴,垂足为D,
∵A、C的坐标分别是(0,2)、(4、0),
∴OA=2,OC=4,
∵∠ACB=90°,
∴∠OAC+∠OCA=∠OCA+∠BCD=90°,
∴∠OAC=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△CDB,
∴,即,
∴CD=1,DB=2,
∴OD=4+1=5,即B(5,2),
把B(5,2)代入得:k=5×2=10,
故选:D.
【点睛】
本题考查了坐标与图形,相似三角形的判定和性质以及反比例函数图象上点的坐标特征,正确的作出辅助线,恰当的将线段的长与坐标互相转化是解题的关键.
6.D
【解析】
【分析】
连接OD、OE,先设OE=x,再证明四边形ODCE是矩形,证明△AOD∽△OBE,再由比例式得出OE的长即可.
【详解】
解:连接OD、OE,
设OE=x,
∵半圆分别与AC、BC相切,
∴∠CDO=∠CEO=90°,
∵∠C=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴OD=CE=OE=CD=x,
∵OE∥BC,
∴△AOE∽△ABC,
∴,
∴,
解得x=,
故选:D.
【点睛】
本题考查了切线的性质.相似三角形的性质与判定,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形,证明三角形相似解决有关问题.
7.C
【解析】
【分析】
根据相似三角形的周长比等于相似比,面积比等于相似比的平方,即可求出面积比.
【详解】
∵△ABC∽△A B C ,且△ABC与△A B C 的周长比为
∴△ABC与△A B C 的相似比为
∴△ABC与△A B C 的面积比为
故选C.
【点睛】
此题考查的是相似三角形的性质,掌握相似三角形的周长比等于相似比,面积比等于相似比的平方是解决此题的关键.
8.D
【解析】
【详解】
在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
解:设电视塔的高度应是x,根据题意得:=,
解得:x=125米.
故选D.
命题立意:考查利用所学知识解决实际问题的能力.
9.A
【解析】
【详解】
∵△ABC∽△DEF,且相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故选A.
10.C
【解析】
【分析】
由折叠的性质可得出,结合平角等于180°即可求出∠CDE和∠CED的度数,再在△CDE中,利用三角形内角和定理可求出∠C的度数.
【详解】
由折叠的性质可得出,,
,
,
在中,,
,
故选:C
【点睛】
本题考查了三角形内角和定理、折叠的性质以及补角,利用折叠的性质及平角等于180°,求出∠CDE和∠CED的度数是解题的关键.
11.D
【解析】
【分析】
利用相似三角形的对应角相等即可得到答案.
【详解】
∵△ABC是等腰三角形,AB=AC,∠A=30°,∴∠C=(180°﹣∠A)÷2=75°.
∵△ABC∽△A′B′C′,∴∠C′=∠C=75°.
故选D.
【点睛】
本题考查了等腰三角形的性质及相似三角形的性质,解题的关键是利用等腰三角形的性质求得等腰三角形底角的度数.
12.
【解析】
【分析】
连接BF,根据正方形的性质和勾股定理求出BF,再根据中位线定理求解即可.
【详解】
解:如图,连接BF,
∵正方形ABCD和正方形CEFG中,,,
∴,,
∴,
∴
∴,
∵、为AB,AF中点,
∴,
故答案为:.
【点睛】
本题考查了正方形的性质,勾股定理,中位线定理,解题的关键是求出BF的长.
13.16cm
【解析】
【分析】
由三角形相似可得对应边分别成比例.
【详解】
解:设△DEF的最长边长x,则由题意得:
,解得x=16,
故答案为:16.
【点睛】
本题考察了相似比的定义.
14.
【解析】
【分析】
利用△BFE∽△DFA,可求出△DFA的面积,再利用来求出△BAF的面积,即可得△ABD的面积,它的2倍即为的面积.
【详解】
解:中,BE∥AD,
∴△BFE∽△DFA,
∴.
而△BEF的面积是1,
∴S△DFA=.
又∵△BFE∽△DFA
∴.
∵,即可知S△BAF=.
而S△ABD=S△BAF+S△DFA
∴S△AFD=.
∴ ABCD的面积=×2=.
故答案为.
【点睛】
本题考查的是利用相似形的性质求面积,把握相似三角形的面积比等于相似比的平方是解决本题的重点.
15.10
【解析】
【分析】
如图(见解析),先根据等腰直角三角形的判定与性质可得,再根据平行线的性质可得,从而可得,然后根据相似三角形的判定与性质可得,设,利用线段的和差可求出x的值,最后利用勾股定理可求出AG的长,由此在中,利用勾股定理即可得.
【详解】
如图,连接AC,过点G作于点D
,
是等腰直角三角形
在和中,
,即
设,则,
解得
又
则在中,由勾股定理得:
故答案为:10.
【点睛】
本题考查了平行线的性质、等腰直角三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识点,通过作辅助线,构造相似三角形是解题关键.
16.
【解析】
【分析】
根据可得,把a,c,e代入所求代数式中,约分后即可求得结果.
【详解】
∵
∴
∴
故答案为:
【点睛】
本题考查了比例的性质,求代数式的值,根据比例的性质变形是关键.
17.见解析;①90;②直径所对的圆周角是直角;③
【解析】
【分析】
根据直径所对的圆周角是直角,和同弧所对的圆周角相等即可得出结论
【详解】
解:补全的图形如图1所示.
①∵OQ是直径
∴∠OPQ=90°
故答案为:90;
②故答案为:直径所对的圆周角是直角;
③∵CE⊥PQ
∴由垂径定理得:.
故答案为:
【点睛】
本题考查圆周角定理的推论,垂径定理,熟练掌握圆周角定理及推论是关键
18.1:3
【解析】
【分析】
由两个相似三角形的面积比是1:9,根据相似三角形的面积比等于相似比的平方,即可求得答案.
【详解】
解:∵两个相似三角形的面积比是1:9,
∴这两个三角形的相似比是:1:3.
故答案为1:3.
【点睛】
本题考查了相似三角形的性质.此题比较简单,注意掌握定理的应用是解此题的关键.
19.
【解析】
【分析】
根据比例的性质,可用b表示a,根据分式的性质,即可得到答案.
【详解】
解:∵
∴
∴
故答案为:.
【点睛】
本题考查了比例的性质,利用比例的性质得出是解题关键,又利用了分式的性质.
20.50
【解析】
【详解】
5×1000000=5000000(cm)
=50km
21.3:2;
【解析】
【分析】
由AG//BC可得△AFG与△BFD相似 ,△AEG与△CED相似,根据相似比求解.
【详解】
假设:AF=3x,BF=5x ,
∵△AFG与△BFD相似
∴AG=3y,BD=5y
由题意BC:CD=3:2则CD=2y
∵△AEG与△CED相似
∴AE:EC= AG:DC=3:2.
【点睛】
本题考查的是相似三角形,熟练掌握相似三角形的性质是解题的关键.
22.7.5
【解析】
【分析】
利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小颖同学的身高即可求得树高AB.
【详解】
解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴,
∵DE=8cm=0.08m,DF=10cm=0.1m,AC=1.5m,CD=8m,
∴由勾股定理求得EF=0.06m,
∴,
∴BC=6米,
∴AB=AC+BC=1.5+6=7.5(米).
故答案为:7.5.
【点睛】
本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形的模型.
23.AH为1255步,HB为30750步
【解析】
【分析】
根据题意得出△FCB∽△FAH,△EDG∽△AHG,进而利用相似三角形的性质求出即可.
【详解】
解:由题意,得,AH⊥HG,CB⊥HG,
∴∠AHF=90°,∠CBF=90°,
∴∠AHF=∠CBF,
∵∠AFB=∠CFB,
∴△CBF∽△AHF,
∴
同理可得
∵BF=123,BD=1000,DG=127,
∴HF=HB+123,HG=HB+1000+127=HB+1127,BC=DE=3丈=3×=5步,
∴
解得HB=30750,HA=1255步,
答:AH为1255步,HB为30750步.
【点睛】
本题考查了相似三角形的应用,解题的关键是掌握相似三角形的判定和性质.
24.(1)AF=1或3;(2)见解析;(3)见解析.
【解析】
【详解】
试题分析:
(1)由题意可知,∠A=∠B=90°,由此可知要使△AEF与△BCF相似,存在两种情况:①当∠AEF=∠BFC时,若,则两三角形相似;②当∠AEF=∠BCF时, 若,则两三角形相似;由这两种情况分别根据已知条件进行计算即可得到相应的AF的值;
(2)如下图所示:①延长DA到E′,使AE′=AE,连接CE′交AB于点F1;②连接CE,以CE为直径作圆,分别交AB于点F2、F3;则F1、F2、F3为所求点;
(3)结合(1)(2)可知,当m=3时,符合条件的点F有2个,当m=4时,符合条件的点F也有2个,而当1
试题解析:
(1)①当∠AEF=∠BFC时,
要使△AEF∽△BFC,需,即,
解得AF=1或3;
②当∠AEF=∠BCF时,
要使△AEF∽△BCF,需=,即,
解得AF=1;
综上所述AF=1或3
(2)如下图所示,图中F1、F2、F3为所求点;
(提示:延长DA,作点E关于AB的对称点E′,连结CE′,交AB于点F1;连结CE,以CE为直径作圆交AB于点F2、F3);
(3)如(2)中所作图形,
当m=4时,由已知条件可得DE=3,则CE=5,即图中圆的直径为5,由梯形中位线定理可得此时图中所作圆的圆心到AB的距离=2.5=所作圆的半径,F2和F3重合,即当m=4时,符合条件的F有2个;
当m>4时,图中所作圆和AB相离,此时F2和F3不存在了,即此时符合条件的F只有F11个;
而当1<m<4且m≠3时,由所作图形可知,符合条件的F有3个;
综上所述:可得:①当1<m<4且m≠3时,符合条件的F有3个; ②当m=3时,符合条件的F有2个;③当m=4时,符合条件的F有2个;④当m>4时,符合条件的F有1个.
25.(1)详见解析;(2)详见解析;(3)详见解析
【解析】
【分析】
(1)设正方形ABCD的边长为1,则AB=AD=1,由勾股定理得出,得出,求出,由正方形的性质得出,求出,即可得出结论;
(2)由正方形和矩形的性质得出∠EAB=∠BCD=90°,AC=CD=AE=DE=BF,BC=DF,由点C为线段AB的黄金分割点,得出,因此,即可得出结论;
(3)根据正五边形的性质得到∠DAE=∠DAE,∠ADE=∠AEM=36°,推出△AME∽△AED,根据相似三角形的性质得到∴AE:AD=AM:AE,得到AE2=AD AM,等量代换即可得到结论.
【详解】
(1)证明:设正方形ABCD的边长为1,则AB=AD=1,
∵E为AD中点,
∴AE=,
∴在Rt△BAE中,
∵EF=BE
∴
∴,
∵四边形AFGH是正方形,
∴,
∴,
∴点H是线段AB的黄金分割点;
(2)证明:∵四边形ACDE是正方形,四边形CBFD是矩形,
∴∠EAB=∠BCD=90°,AC=CD=AE=DE=BF,BC=DF,
∵点C为线段AB的黄金分割点,
∴,
∴,
∴△EAB∽△BCD;
(3)证明:∵五边形ABCDE是正五边形,
∴∠BAE=∠AED=(5-2)×180°=108°,AB=AE=DE,
∴∠ABE=∠AEM=∠DAE=∠ADE=(180°-108°)=36°,
∵∠DAE=∠DAE,∠ADE=∠AEM=36°,
∴△AME∽△AED,
∴AE:AD=AM:AE,
∴AE2=AD AM,
∵AE=DE=DM,
∴DM2=AD AM,
∴点M是AD的黄金分割点.
【点睛】
本题是相似形综合题目,考查了相似三角形的判定与性质、黄金分割、正方形的性质、矩形的性质、正五边形的性质、勾股定理、等腰三角形的性质等知识;本题综合性强,熟练掌握黄金分割和正方形的性质以及正五边形的性质,证明三角形相似是解题的关键.
26.(1);(2)图见解析.
【解析】
【分析】
(1)利用三角形的中位线定理以及三角形法则解答即可;
(2)利用平行四边形的法则作图即可.
【详解】
解:(1)∵AE=ED,BF=DF,
∴EF∥AB,EF=AB,
∴=,
∵BF=DF,BG=GC,
∴FG∥CD,FG=DC=AC,
∴=,
∵=+,
∴.
(2)如图所示,图中,即为所求.
【点睛】
本题考查了三角形的中位线定理、三角形法则、平行四边形法则以及常见作图等知识,熟练掌握以上基本知识是解题的关键.
27.(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.
【解析】
【详解】
试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;
(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.
试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
,
∴△AGE≌△AFE(SAS);
(2)设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.
则△ADF≌△ABG,DF=BG.
由(1)知△AEG≌△AEF,
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NF=DF,
∴a﹣BE=a﹣DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MG=BM=DF=NF,
∴EF2=ME2+NF2;
(3)EF2=2BE2+2DF2.
如图所示,延长EF交AB延长线于M点,交AD延长线于N点,
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.
由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM﹣GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,
即2(DF2+BE2)=EF2
考点:四边形综合题
答案第1页,共2页
答案第1页,共2页
