圆与圆的位置关系
图片预览






文档简介
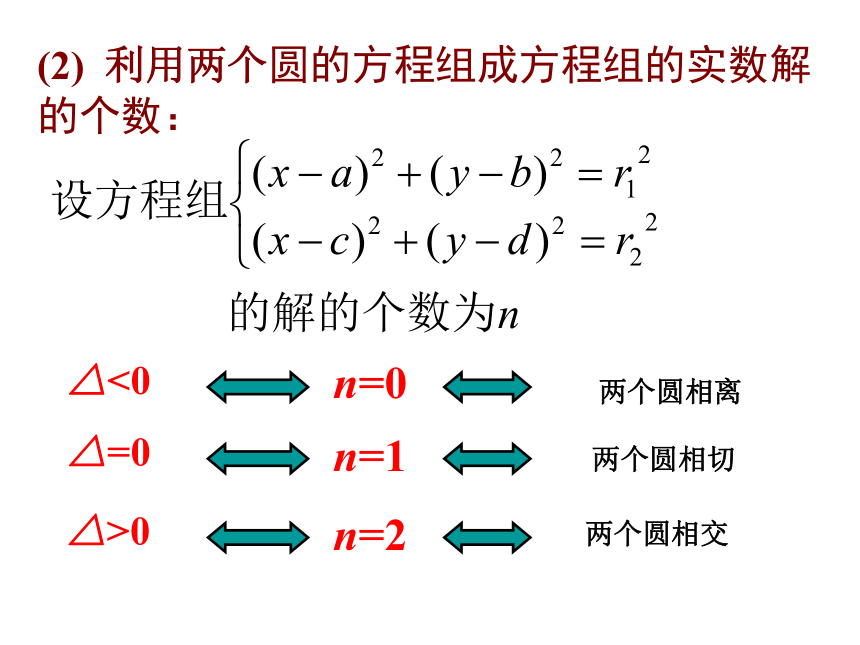
课件31张PPT。复习回顾:直线与圆的位置关系:相离、相交、相切判断直线与圆的位置关系有哪些方法?(1)根据圆心到直线的距离;(2)根据直线的方程和圆的方程组成方程组的实数解的个数;4.2.2 圆与圆的位置关系两圆的位置关系 平面上两圆的位置关系有五种:
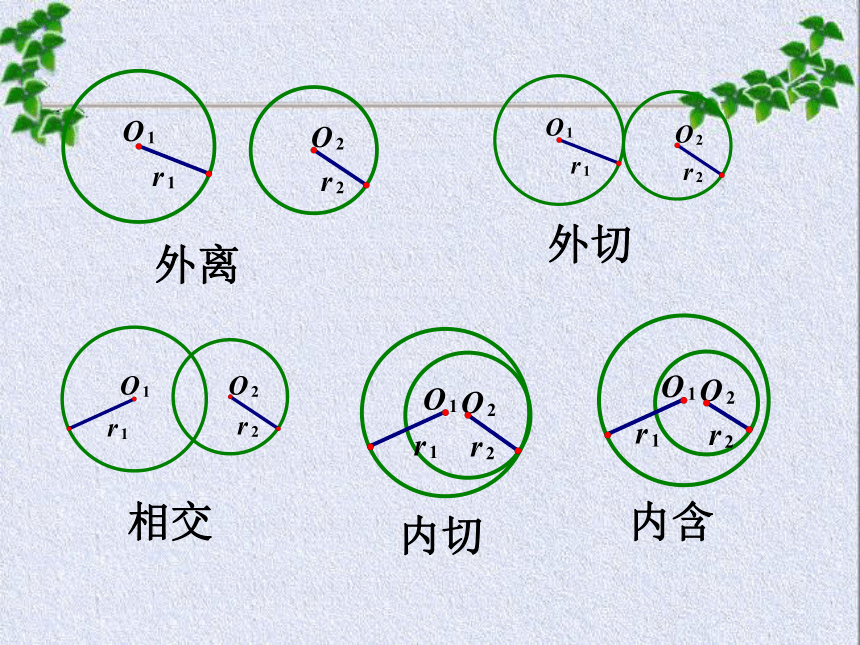
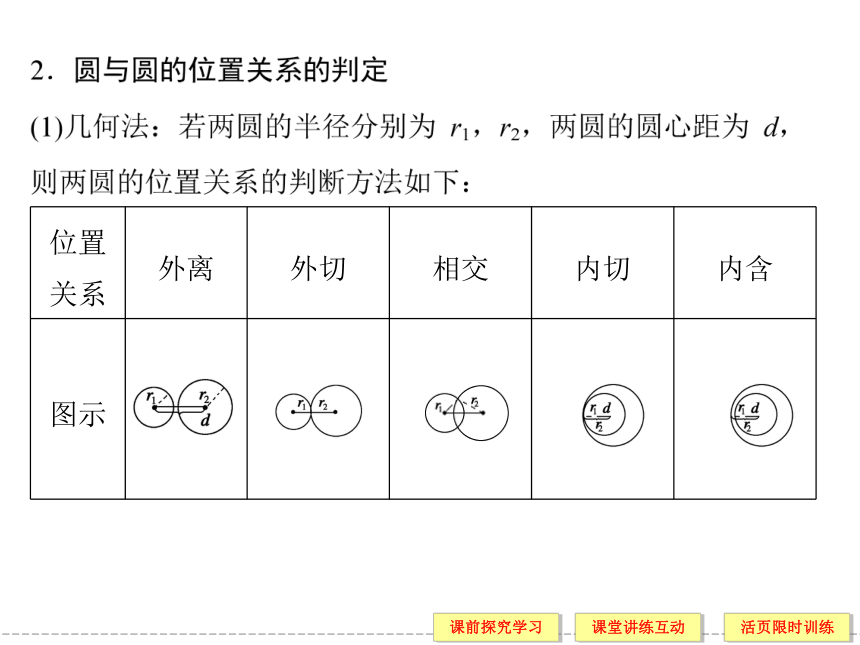
(1)两圆外离
(2)两圆外切
(3)两圆相交
(4)两圆内切
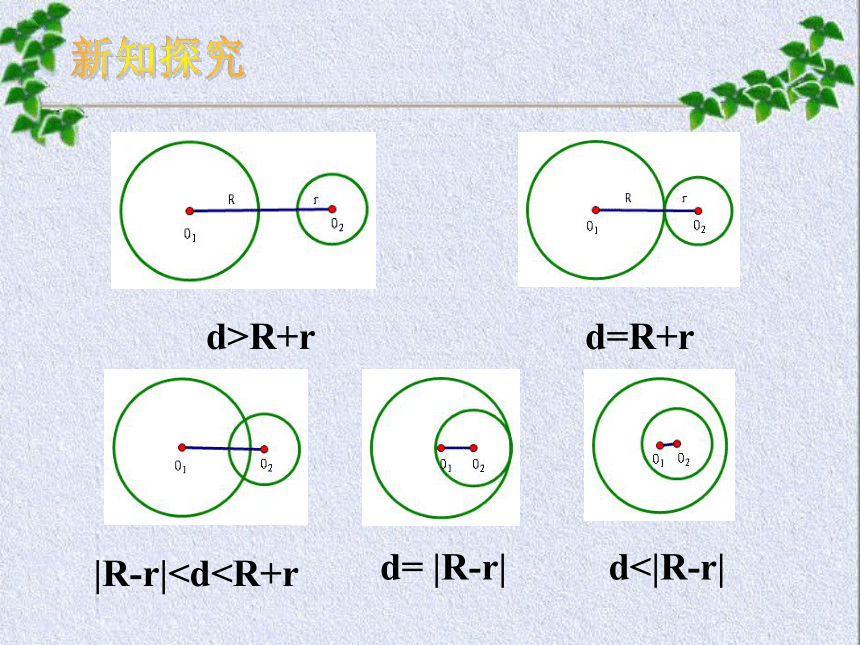
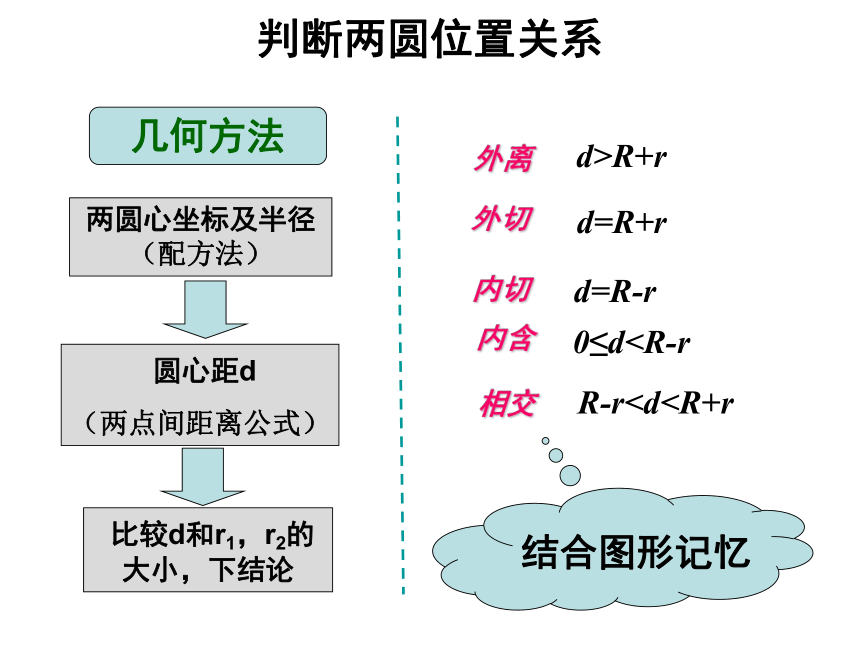
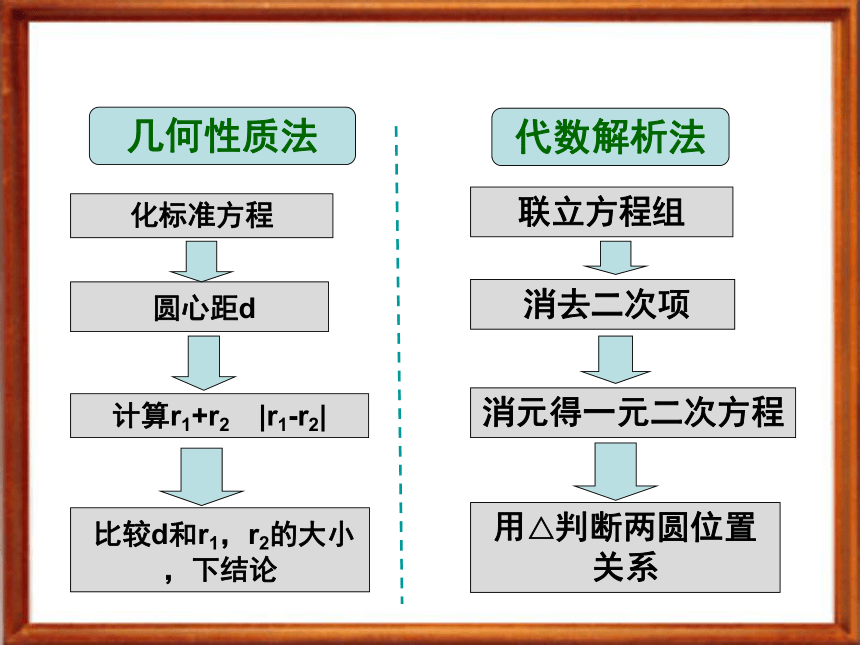
(5)两圆内含外离外切相交内切内含外离 外切 相交 内切 内含 两圆位置关系的判断 已知圆C1:(x-a)2+(y-b)2=r12与圆C2:(x-c)2+(y-d)2=r22,它们的位置关系有两种判断方法:(1)平面几何法判断圆与圆的位置关系公式: 第一步:计算两圆的半径r1,r2;
第二步:计算两圆的圆心距d;
第三步:根据d与r1,r2之间的关系,判断两圆的位置关系 d>R+rd=R+rd= |R-r||R-r|(两点间距离公式) 比较d和r1,r2的大小,下结论外离d>R+rd=R+rR-rr1+r2d=r1+r2r1+r2d=|r1-r2||r1-r2|解法一:把圆C1和圆C2的方程化为标准方程:例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.所以圆C1与圆C2相交,它们有两个公共点A,B.例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.解法二:圆C1与圆C2的方程联立,得(1)-(2),得 所以,方程(4)有两个不相等的实数根x1,x2,把x1,x2分别代入方程(3):
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2). 例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.两圆的公共弦方程得到y1,y2. 1.若两圆C1:x2+y2+D1x+E1y+F1=0和
C2:x2+y2+D2x+E2y+F2=0
相交,则其公共弦所在直线的方程是
(D1-D2)x+(E1-E2)y+F1-F2=0,
拓展练习:课本130页解 两圆的圆心距d= =5.
两圆的半径分别为r1=1和r2=r(r>1).
因为两圆相交,所以r2-r1<d<r1+r2,
即r-1<5<1+r,
即 解得
从而实数r的取值范围为(4,6).课堂小结:外离外切相交内切内含01210d>R+r
d=R+r
R-r圆的外部一圆在另一
圆的外部两圆相交一圆在另一
圆的内部一圆在另一
圆的内部名称活页规范训练2.圆C1:x2+y2+4x-4y+4=0与圆C2:x2+y2-4x-10y+13=0的公切线有( ).
A.1条 B.2条 C.3条 D.4条
解析 C1(-2,2),r1=2,C2(2,5),r2=4,
|C1C2|= =5,
r2-r1<|C1C2|<r1+r2,
圆C1与圆C2相交,故选B.
答案 B4.若a2+b2=4,则两圆(x-a)2+y2=1与x2+(y-b)2=1的位置关系是________.
解析 ∵两圆的圆心分别为O1(a,0),O2(0,b),半径r1=r2=1,
∴|O1O2|= =2=r1+r2,
两圆外切.
答案 外切5.点P在圆O:x2+y2=1上运动,点Q在圆C:(x-3)2+y2=1上运动,则|PQ|的最小值为________.设连心线OC与圆O交于点P′,与圆C交于点Q′,当点P在P′处,点Q在Q′处时|PQ|最小,最小值为|P′Q′|=|OC|-r1-r2=1.
答案 1解析 如下图.9.两圆相交于两点(1,3)和(m,-1),两圆圆心都在直线x-y+c=0上,则m+c的值为________.
解析 由平面几何性质知:两相交圆圆心的连线与两圆的公共弦垂直,且经过弦的中点,
则 =-1,得m=5,
∴弦中点坐标为(3,1),
∴3-1+c=0,得c=-2,
∴m+c=3.
答案 310.一束光线从点A(-1,1)出发经x轴反射到圆(x-2)2+(y-3)2=1上的最短距离为________.
解析 A关于x轴的对称点为A′(-1,-1),
A′与圆心的距离为 =5,
最短距离为5-1=4.
答案 4
(1)两圆外离
(2)两圆外切
(3)两圆相交
(4)两圆内切
(5)两圆内含外离外切相交内切内含外离 外切 相交 内切 内含 两圆位置关系的判断 已知圆C1:(x-a)2+(y-b)2=r12与圆C2:(x-c)2+(y-d)2=r22,它们的位置关系有两种判断方法:(1)平面几何法判断圆与圆的位置关系公式: 第一步:计算两圆的半径r1,r2;
第二步:计算两圆的圆心距d;
第三步:根据d与r1,r2之间的关系,判断两圆的位置关系 d>R+rd=R+rd= |R-r||R-r|
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2). 例3、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.两圆的公共弦方程得到y1,y2. 1.若两圆C1:x2+y2+D1x+E1y+F1=0和
C2:x2+y2+D2x+E2y+F2=0
相交,则其公共弦所在直线的方程是
(D1-D2)x+(E1-E2)y+F1-F2=0,
拓展练习:课本130页解 两圆的圆心距d= =5.
两圆的半径分别为r1=1和r2=r(r>1).
因为两圆相交,所以r2-r1<d<r1+r2,
即r-1<5<1+r,
即 解得
从而实数r的取值范围为(4,6).课堂小结:外离外切相交内切内含01210d>R+r
d=R+r
R-r
圆的外部两圆相交一圆在另一
圆的内部一圆在另一
圆的内部名称活页规范训练2.圆C1:x2+y2+4x-4y+4=0与圆C2:x2+y2-4x-10y+13=0的公切线有( ).
A.1条 B.2条 C.3条 D.4条
解析 C1(-2,2),r1=2,C2(2,5),r2=4,
|C1C2|= =5,
r2-r1<|C1C2|<r1+r2,
圆C1与圆C2相交,故选B.
答案 B4.若a2+b2=4,则两圆(x-a)2+y2=1与x2+(y-b)2=1的位置关系是________.
解析 ∵两圆的圆心分别为O1(a,0),O2(0,b),半径r1=r2=1,
∴|O1O2|= =2=r1+r2,
两圆外切.
答案 外切5.点P在圆O:x2+y2=1上运动,点Q在圆C:(x-3)2+y2=1上运动,则|PQ|的最小值为________.设连心线OC与圆O交于点P′,与圆C交于点Q′,当点P在P′处,点Q在Q′处时|PQ|最小,最小值为|P′Q′|=|OC|-r1-r2=1.
答案 1解析 如下图.9.两圆相交于两点(1,3)和(m,-1),两圆圆心都在直线x-y+c=0上,则m+c的值为________.
解析 由平面几何性质知:两相交圆圆心的连线与两圆的公共弦垂直,且经过弦的中点,
则 =-1,得m=5,
∴弦中点坐标为(3,1),
∴3-1+c=0,得c=-2,
∴m+c=3.
答案 310.一束光线从点A(-1,1)出发经x轴反射到圆(x-2)2+(y-3)2=1上的最短距离为________.
解析 A关于x轴的对称点为A′(-1,-1),
A′与圆心的距离为 =5,
最短距离为5-1=4.
答案 4
