14.1 勾股定理(第一课时)说课
文档属性
| 名称 | 14.1 勾股定理(第一课时)说课 |

|
|
| 格式 | zip | ||
| 文件大小 | 808.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-08 21:48:25 | ||
图片预览










文档简介
课件34张PPT。勾股定理华东师大版 义务教育课程标准实验教科书
《数学》八年级(上) 第14章 第1节
说课程序:四、教法学法三、过程分析五、评价分析一、教材分析二、目的分析一、教材分析(一)教材所处的地位和作用(二)教学重点、难点、关键(一)教材所处的地位和作用
勾股定理是在学生已经掌握了三角形的一些知识,经历过图形面积与代数恒等式之间的关系的探索过程的基础上进行学习的。它揭示了直角三角形中三边之间的数量关系,体现了数与形的完美结合。
勾股定理在现实世界中有着广泛的应用,利用它可以解决一些有关直角三角形的问题。
此外,勾股定理的发现过程和验证方法蕴含着丰富的人文和科学价值,为学生后续学习中合情推理的应用、动手实践打下坚实的基础。
本节课选自华师版《数学》八年级上册第十四章“勾股定理”中的第一节第一课时。 (二)教学重点、难点、关键:【教学重点】勾股定理的探索过程。
【教学难点】勾股定理的发现和验证。
【教学关键】
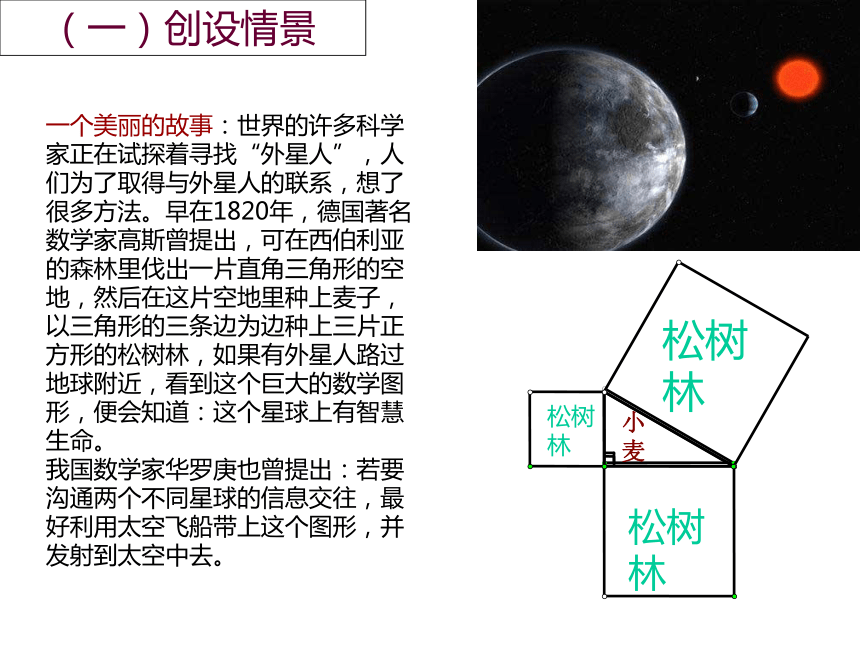
运用“脚手架”理论.借助网格图 进行辅助教学,并通过数形结合,引导学生自主探索。 二、目的分析【知识与技能目标】【过程与方法目标】【情感态度与价值观】【知识与技能目标】 在探索勾股定理的过程中掌握直角三角形三边之间的数量关系,能初步运用勾股定理进行简单的计算。【过程与方法目标】 在探索勾股定理的过程中,让学生经历“观察-猜想-归纳-验证”的过程,体会数形结合和从特殊到一般的思想方法。并通过勾股定理的发现与验证,发展学生的合情推理能力,增强学生的操作探究能力。【情感态度与价值观】 通过介绍我国古代研究勾股定理方面的成就,激发学生热爱祖国和热爱祖国悠久文化的思想感情,培养学生的民族自豪感和钻研精神。三、过程分析(一)创设情景(二)探索规律(三)验证定理(四)问题解决(五)课堂拓展(六)课堂小结(七)布置作业(一)创设情景一个美丽的故事:世界的许多科学家正在试探着寻找“外星人”,人们为了取得与外星人的联系,想了很多方法。早在1820年,德国著名数学家高斯曾提出,可在西伯利亚的森林里伐出一片直角三角形的空地,然后在这片空地里种上麦子,以三角形的三条边为边种上三片正方形的松树林,如果有外星人路过地球附近,看到这个巨大的数学图形,便会知道:这个星球上有智慧生命。
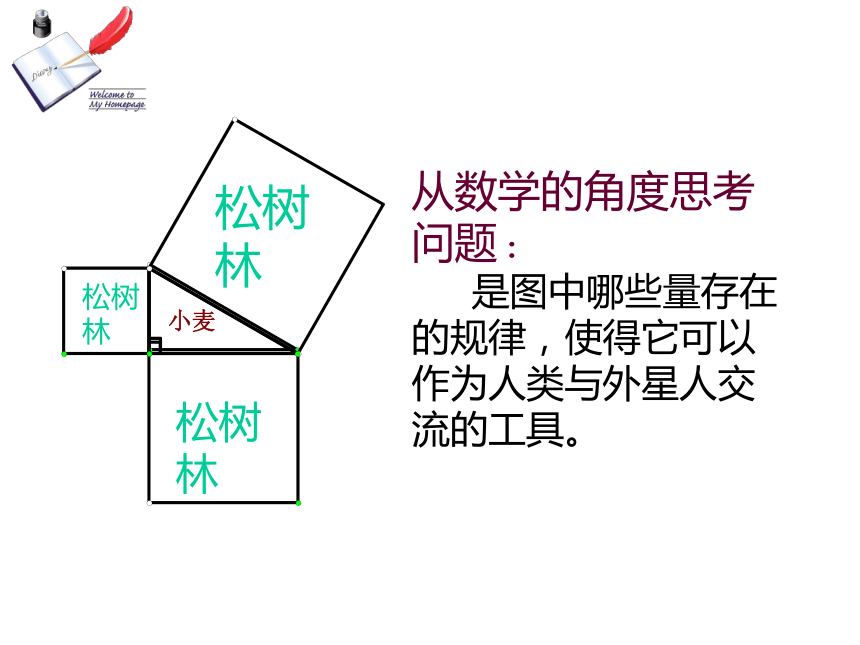
我国数学家华罗庚也曾提出:若要沟通两个不同星球的信息交往,最好利用太空飞船带上这个图形,并发射到太空中去。小麦松树林松树林松树林从数学的角度思考 问题:
是图中哪些量存在的规律,使得它可以作为人类与外星人交流的工具。相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映了这一规律。
同学们,
我们也来观察下面的图案,看看你能发现什么?(二)探索规律1、探索:(1)请同学们认真观察图1、图2,并填表图1 图2(2)在方格纸上,画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的两直角边a、b和斜边c为一边向三角形外作正方形P、Q、R, 并结合图形将相应数据填入表格中。(图中每个小方格代表一个单位面积)1、探索:(1)请同学们认真观察图1、图2,并填表1 1 1 1 2图1(二)探索规律1、探索:(1)请同学们认真观察图1、图2,并填表1 1 1 1 2图24 3 16 9(二)探索规律图形的“割”图形的“补”(二)探索规律图形的“割”图形的“补”(二)探索规律1、探索:(1)请同学们认真观察图1、图2,并填表1 1 1 1 2图24 3 16 925(二)探索规律1、探索:(2)在方格纸上,画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的两直角边a、b和斜边c为一边向三角形外作正方形P、Q、R, 并结合图形将相应数据填入表格中。
(二)探索规律1 1 1 1 24 3 16 925(二)探索规律 2 4 4 8
2 1 4 5
3 4 9 13
4 5 16 25 411 1 1 1 2 4 3 16 9 25SP+SQ=SR(二)探索规律2、验证猜想,得出定理探索(二)探索规律规律: SP+SQ=SR即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。思考:如果只有直角三角形,而没有向外作正方形,那么直角三角形三边之间又存在什么规律。你能用文字语言表达出来吗? (二)探索规律2、归纳猜想,得出定理勾股定理如果直角三角形两直角边分别为a、b,斜边为c.那么即直角三角形两直角边的平方和等于 斜边的平方。
(毕达哥拉斯定理)勾股弦(二)探索规律 本环节设计遵循“建构主义”的学习理念,以学生为中心,强调学生对知识的主动探索、主动发现和对所学知识意义的主动建构。
教师只是给学生提供一定的学习“情景”,在此“情景”中,学生通过“协作”、“会话”和“意义建构”进行有效学习。赵爽证法毕达哥拉斯法(三)验证定理问题:如图,将长为5.41米的梯子AC斜靠在墙上,BC为2.16米,求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)(四)问题解决解: 在Rt△ABC中,∠ABC=90゜, BC=2.16, AC=5.41, 根据勾股定理得 AB=≈4.96(米) 美丽的勾股树——让学生感受数学美的同时,勾股史话——让学生了解勾股定理的历史与现状。(五)课堂拓展了解勾股树的构造美丽勾股树 中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。
在国外,相传勾股定理是公元前550年时古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。 (五)课堂拓展勾股史话这节课你有哪些收获?你能谈谈你对这节课的感受吗?
1、巩固型作业:课本P54习题14.1 1,2,3
2、拓展型作业:通过上网,搜索有关勾股定理的知识:如(1)勾股定理的历史;(2)勾股定理的证明方法;(3)勾股定理在实际生活中的应用。并制作成研究性学习报告。(六)课堂小结(七)布置作业 数学教学是数学活动的教学,是师生之间交往互动和共同发展的过程,学生是活动的主体,教师起主导作用。
因此,根据本节教材内容和编排特点并针对八年级学生的知识结构和认知规律,为了更有效的突出重点,突破难点,本节课采用探究发现式教学,由浅入深,由特殊到一般地提出问题。并利用多媒体辅助教学,使教学直观形象。引导学生亲身观察,大胆猜想,自主探索,合作交流。让学生感受到自己是数学学习的主人,体会到生活中处处有数学。(一)教法分析四、教法学法(二)学法分析 新课标明确提出要培养“可持续发展的学生”,因此教师要有目的、有针对性的引导学生参入到学习活动中,鼓励学生采用自主探索,合作交流的研讨式学习方式,培养学生“动手”、“动脑”、“动口”的习惯与能力,使学生真正成为学习的主人五、评价分析 勾股定理的学习让学生经历了主动参与、积极探索数学知识的过程,并且了解了勾股定理的发展历史。 在教学过程中,我创设了有助于激发学生学习兴趣的问题情境,引导学生探索直角三角形三边的关系。借助“网格图”进行辅助教学,结合多媒体动画的演示,加深学生对勾股定理的理解,突破了难点,及时用例题加以巩固所学知识,课堂小结从知识内容和数学思想方法等方面展开,既有知识的总结,又有方法的提炼,有利于培养学生学知识、用知识的意识,增强学好数学的信心,体现了学生的主体地位,使学生在不断解决问题的过程中,掌握了知识,训练了能力,体验了情感。 谢谢指导!
《数学》八年级(上) 第14章 第1节
说课程序:四、教法学法三、过程分析五、评价分析一、教材分析二、目的分析一、教材分析(一)教材所处的地位和作用(二)教学重点、难点、关键(一)教材所处的地位和作用
勾股定理是在学生已经掌握了三角形的一些知识,经历过图形面积与代数恒等式之间的关系的探索过程的基础上进行学习的。它揭示了直角三角形中三边之间的数量关系,体现了数与形的完美结合。
勾股定理在现实世界中有着广泛的应用,利用它可以解决一些有关直角三角形的问题。
此外,勾股定理的发现过程和验证方法蕴含着丰富的人文和科学价值,为学生后续学习中合情推理的应用、动手实践打下坚实的基础。
本节课选自华师版《数学》八年级上册第十四章“勾股定理”中的第一节第一课时。 (二)教学重点、难点、关键:【教学重点】勾股定理的探索过程。
【教学难点】勾股定理的发现和验证。
【教学关键】
运用“脚手架”理论.借助网格图 进行辅助教学,并通过数形结合,引导学生自主探索。 二、目的分析【知识与技能目标】【过程与方法目标】【情感态度与价值观】【知识与技能目标】 在探索勾股定理的过程中掌握直角三角形三边之间的数量关系,能初步运用勾股定理进行简单的计算。【过程与方法目标】 在探索勾股定理的过程中,让学生经历“观察-猜想-归纳-验证”的过程,体会数形结合和从特殊到一般的思想方法。并通过勾股定理的发现与验证,发展学生的合情推理能力,增强学生的操作探究能力。【情感态度与价值观】 通过介绍我国古代研究勾股定理方面的成就,激发学生热爱祖国和热爱祖国悠久文化的思想感情,培养学生的民族自豪感和钻研精神。三、过程分析(一)创设情景(二)探索规律(三)验证定理(四)问题解决(五)课堂拓展(六)课堂小结(七)布置作业(一)创设情景一个美丽的故事:世界的许多科学家正在试探着寻找“外星人”,人们为了取得与外星人的联系,想了很多方法。早在1820年,德国著名数学家高斯曾提出,可在西伯利亚的森林里伐出一片直角三角形的空地,然后在这片空地里种上麦子,以三角形的三条边为边种上三片正方形的松树林,如果有外星人路过地球附近,看到这个巨大的数学图形,便会知道:这个星球上有智慧生命。
我国数学家华罗庚也曾提出:若要沟通两个不同星球的信息交往,最好利用太空飞船带上这个图形,并发射到太空中去。小麦松树林松树林松树林从数学的角度思考 问题:
是图中哪些量存在的规律,使得它可以作为人类与外星人交流的工具。相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映了这一规律。
同学们,
我们也来观察下面的图案,看看你能发现什么?(二)探索规律1、探索:(1)请同学们认真观察图1、图2,并填表图1 图2(2)在方格纸上,画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的两直角边a、b和斜边c为一边向三角形外作正方形P、Q、R, 并结合图形将相应数据填入表格中。(图中每个小方格代表一个单位面积)1、探索:(1)请同学们认真观察图1、图2,并填表1 1 1 1 2图1(二)探索规律1、探索:(1)请同学们认真观察图1、图2,并填表1 1 1 1 2图24 3 16 9(二)探索规律图形的“割”图形的“补”(二)探索规律图形的“割”图形的“补”(二)探索规律1、探索:(1)请同学们认真观察图1、图2,并填表1 1 1 1 2图24 3 16 925(二)探索规律1、探索:(2)在方格纸上,画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的两直角边a、b和斜边c为一边向三角形外作正方形P、Q、R, 并结合图形将相应数据填入表格中。
(二)探索规律1 1 1 1 24 3 16 925(二)探索规律 2 4 4 8
2 1 4 5
3 4 9 13
4 5 16 25 411 1 1 1 2 4 3 16 9 25SP+SQ=SR(二)探索规律2、验证猜想,得出定理探索(二)探索规律规律: SP+SQ=SR即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。思考:如果只有直角三角形,而没有向外作正方形,那么直角三角形三边之间又存在什么规律。你能用文字语言表达出来吗? (二)探索规律2、归纳猜想,得出定理勾股定理如果直角三角形两直角边分别为a、b,斜边为c.那么即直角三角形两直角边的平方和等于 斜边的平方。
(毕达哥拉斯定理)勾股弦(二)探索规律 本环节设计遵循“建构主义”的学习理念,以学生为中心,强调学生对知识的主动探索、主动发现和对所学知识意义的主动建构。
教师只是给学生提供一定的学习“情景”,在此“情景”中,学生通过“协作”、“会话”和“意义建构”进行有效学习。赵爽证法毕达哥拉斯法(三)验证定理问题:如图,将长为5.41米的梯子AC斜靠在墙上,BC为2.16米,求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)(四)问题解决解: 在Rt△ABC中,∠ABC=90゜, BC=2.16, AC=5.41, 根据勾股定理得 AB=≈4.96(米) 美丽的勾股树——让学生感受数学美的同时,勾股史话——让学生了解勾股定理的历史与现状。(五)课堂拓展了解勾股树的构造美丽勾股树 中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。
在国外,相传勾股定理是公元前550年时古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。 (五)课堂拓展勾股史话这节课你有哪些收获?你能谈谈你对这节课的感受吗?
1、巩固型作业:课本P54习题14.1 1,2,3
2、拓展型作业:通过上网,搜索有关勾股定理的知识:如(1)勾股定理的历史;(2)勾股定理的证明方法;(3)勾股定理在实际生活中的应用。并制作成研究性学习报告。(六)课堂小结(七)布置作业 数学教学是数学活动的教学,是师生之间交往互动和共同发展的过程,学生是活动的主体,教师起主导作用。
因此,根据本节教材内容和编排特点并针对八年级学生的知识结构和认知规律,为了更有效的突出重点,突破难点,本节课采用探究发现式教学,由浅入深,由特殊到一般地提出问题。并利用多媒体辅助教学,使教学直观形象。引导学生亲身观察,大胆猜想,自主探索,合作交流。让学生感受到自己是数学学习的主人,体会到生活中处处有数学。(一)教法分析四、教法学法(二)学法分析 新课标明确提出要培养“可持续发展的学生”,因此教师要有目的、有针对性的引导学生参入到学习活动中,鼓励学生采用自主探索,合作交流的研讨式学习方式,培养学生“动手”、“动脑”、“动口”的习惯与能力,使学生真正成为学习的主人五、评价分析 勾股定理的学习让学生经历了主动参与、积极探索数学知识的过程,并且了解了勾股定理的发展历史。 在教学过程中,我创设了有助于激发学生学习兴趣的问题情境,引导学生探索直角三角形三边的关系。借助“网格图”进行辅助教学,结合多媒体动画的演示,加深学生对勾股定理的理解,突破了难点,及时用例题加以巩固所学知识,课堂小结从知识内容和数学思想方法等方面展开,既有知识的总结,又有方法的提炼,有利于培养学生学知识、用知识的意识,增强学好数学的信心,体现了学生的主体地位,使学生在不断解决问题的过程中,掌握了知识,训练了能力,体验了情感。 谢谢指导!
