苏教版数学四年级下册第七单元《三角形、平行四边形和梯形》单元测试卷(含答案)
文档属性
| 名称 | 苏教版数学四年级下册第七单元《三角形、平行四边形和梯形》单元测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 154.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览




文档简介
苏教版数学四年级下册第七单元《三角形、平行四边形和梯形》单元测试卷
一、选择题
1.用三根小棒围成一个三角形,应选择( )
A.1cm、2cm、3cm B.2cm、3cm、4cm C.4cm、4cm、9cm D.5cm、10cm、20cm
2.如果三角形两条边的长度分别是4cm,7cm,那么第三边不可能是( )
A.10cm B.5cm C.3cm
3.一个三角形中,∠1=50°,∠2=40°.这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形
4.一个平行四边形与一个三角形等底等高,如果把它们的底都扩大2倍,高不变,那么( )
A.它们的面积都不变
B.平行四边形的面积是三角形面积的2倍
C.两个图形的面积相等
D.三角形的面积是平行四边形面积的2倍
5.下图平行线中三个图形的面积( )。
A.都相等 B.三角形面积大 C.梯形面积小 D.平行四边形面积大
二、竖式计算
6.用竖式计算。
三、口算和估算
7.口算.
66+28= 55-38= 80-32=
39+53= 56+24= 63÷3=
21×40= 70×10= 83-57=
四、填空题
8.一个等腰三角形的周长是24 cm,其中一条边长6 cm,那么另外两条边的长分别是( )cm和( )cm.
9.只有一组对边平行的四边形叫做________.
10.一根24厘米长的铁丝,可以围成边长( )厘米的等边三角形,也可以围成边长( )厘米的正方形。
11.猜猜我是什么三角形。
(1)我最大的角是钝角。( )
(2)我有一个角是直角。( )
(3)我有两条边是相等的。( )
(4)我的三条边是相等的。( )
12.一个梯形的上底长2.2厘米,下底长4.8厘米,面积是28平方厘米,它的高是( )厘米.
13.一个等腰三角形的一个底角是55°,这个三角形的顶角是( ),如果它的顶角是20°,那么它的一个底角是( )。
14.在一个三角形中,一条高只有一条对应的底边. .(判断对错)
15.数一数.
(1)
________个
(2)
________个
(3)
________个
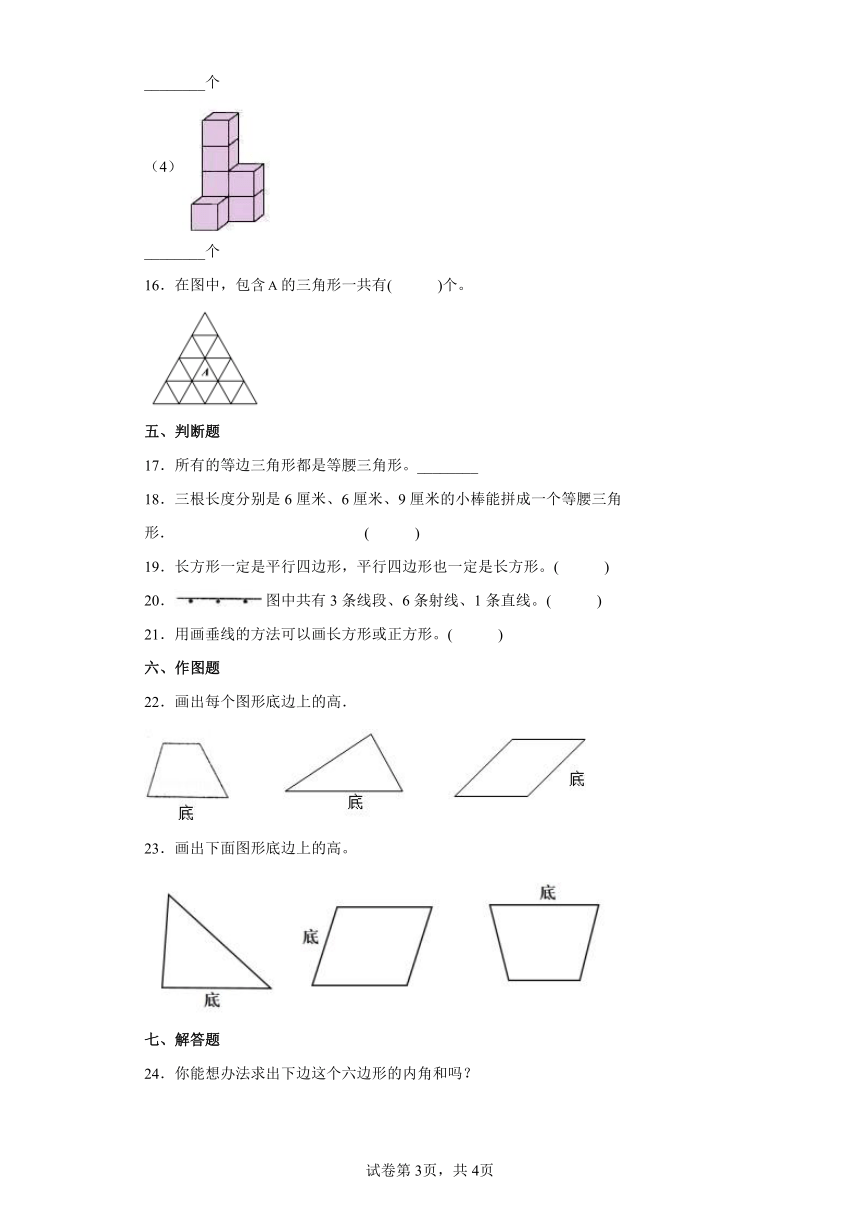
(4)
________个
16.在图中,包含的三角形一共有( )个。
五、判断题
17.所有的等边三角形都是等腰三角形。________
18.三根长度分别是6厘米、6厘米、9厘米的小棒能拼成一个等腰三角形. ( )
19.长方形一定是平行四边形,平行四边形也一定是长方形。( )
20.图中共有3条线段、6条射线、1条直线。( )
21.用画垂线的方法可以画长方形或正方形。( )
六、作图题
22.画出每个图形底边上的高.
23.画出下面图形底边上的高。
七、解答题
24.你能想办法求出下边这个六边形的内角和吗?
25.一个平行四边形的一条边延长27厘米后变成了一个梯形,这个梯形的下底是上底的4倍。这个梯形的上底是多少厘米?
26.解决问题。
27.在一个三角形中,∠1,∠2,∠3为三角形的三个角,已知∠1=45°,∠2比∠1大15°,求∠2和∠3的度数分别是多少。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
试题分析:根据“三角形的两边的和一定大于第三边,两边的差一定小于第三边”进行依次分析,选择即可.
解:A、因为1+2=3,所以不能围成三角形;
B、2+3>5,4﹣2<3,所以能围成三角形;
C、4+4=8,所以不能围成三角形;
D、5+10<20,所以不能围成三角形;
故选B.
点评:解答此题应根据三角形的特性,进行分析、解答即可.
2.C
【解析】
【详解】
试题分析:根据三角形的三边关系求得第三边的取值范围,再看哪个选项内的数不在这个范围内即可.
解:设第三边长x.
根据三角形的三边关系,得7﹣4<x<4+7即:3<x<11(但不能取3厘米和11厘米);
因为3厘米不在第三边长的取值范围内,所以不能取.
故选C.
点评:考查三角形的边时,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.
3.A
【解析】
【分析】
三角形内角和是180度.用和减去其中的两个角的度数,就等于第三个角的度数.
【详解】
180-(50+40)
=180-90
=90(度)
是直角三角形
故答案为直角三角形
4.B
【解析】
【分析】
根据平行四边形的面积是与它等底等高的三角形面积的2倍,如果高不变,底都扩大2倍,那么面积也都会扩大2倍,那么平行四边形依然是等底等高的三角形面积的2倍。
【详解】
平行四边形的面积是与它等底等高的三角形面积的2倍,如果高不变,底都扩大2倍,即平行四边形的底还是等于三角形的底,则面积也都会扩大2倍,那么平行四边形依然是等底等高的三角形面积的2倍。
故选B。
【点睛】
此题主要考查的是平行四边形的面积是与它等底等高的三角形面积的2倍。
5.C
【解析】
【分析】
根据平行四边形的面积公式:S=ah,三角形的面积公式:S=ah,梯形的面积公式:S=(a+b)h,把数据分别代入公式求出它们的面积,然后进行比较即可。
【详解】
4×6=24
8×6÷2
=48÷2
=24
(4+2)×6÷2
=6×6÷2
=18
18<24
故答案为:C
【点睛】
此题主要考查平行四边形、三角形、梯形面积公式的灵活运用,关键是熟记公式。
6.9424;21630;7930;12000。
【解析】
【分析】
根据整数乘法的计算方法进行计算即可。
【详解】
124×76=9424 35×618=21630 305×26=7930 50×240=12000
故答案为:9424;21630;7930;12000。
【点睛】
本题考查的是整数乘法计算方法的运用。
7.94;17;48
92;80;21
840;700;26
【解析】
【详解】
略
8. 9 9
【解析】
【详解】
略
9.梯形
【解析】
【详解】
此题可根据梯形的意义来解答,即只有一组对边平行的四边形叫做梯形.
10. 8 6
【解析】
【分析】
等边三角形的三条边相等,等边三角形的边长=周长÷3。正方形的边长=周长÷4,代入数据计算即可。
【详解】
24÷3=8(厘米)
24÷4=6(厘米)
则围成等边三角形,边长为8厘米,围成正方形,边长为6厘米。
【点睛】
解决本题的关键是熟练掌握等边三角形和正方形的周长公式。等边三角形的周长=边长×3,正方形的周长=边长×4。
11. 钝角三角形 直角三角形 等腰三角形 等边三角形
【解析】
【分析】
(1)有一个角是直角的三角形,叫直角三角形;
(2)有一个角是钝角的三角形,叫钝角三角形;
(3)有两条边相等的三角形是等腰三角形;
(4)三条边都相等的三角形是等边三角形(正三角形)。
【详解】
(1)我最大的角是钝角。(钝角三角形)
(2)我有一个角是直角。(直角三角形)
(3)我有两条边是相等的。(等腰三角形)
(4)我的三条边是相等的。(等边三角形)
【点睛】
熟悉三角形的分类标准是解答此题的关键。
12.8
【解析】
略
13. 70° 80°
【解析】
【分析】
等腰三角形中两个底角相等。根据三角形的内角和为180°可知,等腰三角形的顶角=180°-2×底角,底角=(180°-顶角)÷2。据此解答即可。
【详解】
180°-2×55°
=180°-110°
=70°
则这个三角形的顶角是70°。
(180°-20°)÷2
=160°÷2
=80°
则它的一个底角是80°。
【点睛】
本题考查等腰三角形的性质以及三角形的内角和。等腰三角形中,2×底角+顶角=180°。
14.√.
【解析】
【详解】
试题分析:根据三角形高的概念:在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高;则三角形有3个顶点,所以有3条高,据此解答即可.
解:在一个三角形中,一条高只有一条对应的底边.
点评:此题主要考查了三角形高的含义,要灵活运用.
15. 4 4 9 7
【解析】
【详解】
略
16.9
【解析】
【分析】
设最小的正三角形的边长是1,包含A的正三角形的边长可能是1、2、3、4,分类枚举,最后相加得到总数。
【详解】
设最小的正三角形的边长是1;
包含五角星的边长是1的三角形,1个;
包含五角星的边长是2的三角形, 4个;
包含五角星的边长是3的三角形,3个;
包含五角星的边长是4的三角形,1个;
包含五角星的三角形一共有(个)
【点睛】
分类枚举计数是求解几何计数问题最常用的方法,注意在这里三角形有正放和倒放两种情况。
17.√
【解析】
【分析】
三条边都相等的三角形是等边三角形,两条边相等的三角形是等边三角形。三条边相等中包括了两条边相等,所以等腰三角形中包含了等边三角形,等边三角形是特殊的等腰三角形。
【详解】
根据分析可知,等边三角形是特殊的等腰三角形,即所有的等边三角形都是等腰三角形。
故答案为:√。
【点睛】
本题要求熟练掌握等边三角形和等腰三角形的概念,要明白等边三角形一定是等腰三角形,等腰三角形不一定是等边三角形。
18.√
【解析】
【详解】
略
19.×
【解析】
【分析】
长方形是特殊的平行四边形。
【详解】
长方形具有平行四边形的特点,但平行四边形不具有长方形的特点,所以,平行四边形也一定是长方形是错误的。
【点睛】
掌握长方形是特殊的平行四边形是解题的关键,反过来说法不成立。
20.√
【解析】
【详解】
直线没有端点;长度无限;过一点可以画无数条,过两点只能画一条直线。
射线只有一个端点;长度无限。
线段有两个端点,它是直线的一部分;长度有限。
21.√
【解析】
【分析】
根据长方形和正方形的定义进行判断即可。
【详解】
两组对边分别平行、四个角都是直角的四边形叫做长方形。四条边相等、四个角都是直角的四边形叫做正方形。则用画垂线的方法可以画长方形或正方形。
故答案为:√。
【点睛】
正方形和长方形的四个角都是直角。
22.
【解析】
【详解】
试题分析:经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高;在平行四边形中,从一条边上的任意一点向对边作垂线,这点与垂足间的距离叫做以这条边为底的平行四边形的高,平行四边形有无数条高,习惯上作平行四边形的高时都从一个顶点出发作一边的垂线,用三角板的直角可以画出平行四形的高;梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线用三角板的直角可以画出梯形的一条高.
解:
【点评】此题是考查作三角形、平行四边形、梯形的高.注意作高用虚线,并标出垂足.
23.见详解
【解析】
【分析】
(1)从底边相对的顶点作底边的垂线段即为三角形的高。
(2)从底边对边上一点作底边的垂线段即为平行四边形的高。
(3)从下底上一点作上底的垂线段即为梯形的高。
【详解】
【点睛】
本题主要考查学生对作三角形、平行四边形和梯形高的方法的掌握。
24.方法见详解;720°
【解析】
【分析】
如下图,把六边形的一个顶点与其他不相邻的顶点连接起来,这样就把六边形分成4个三角形,4个三角形的内角和等于六边形的内角和,据此即可解答。
【详解】
如上图,把六边形分成4个三角形,三角形的内角和等于180°。
180°×4=720°
答:六边形的内角和等于720°。
【点睛】
本题主要考查学生观察和分析问题的能力。
25.9厘米
【解析】
【分析】
梯形的下底是上底的4倍,所以下底比上底多3倍,据此求解。
【详解】
27÷(4-1) =9(厘米)
答:这个梯形的上底是9厘米。
【点睛】
简单的差倍问题,较小数=差÷(倍数-1)。
26.20厘米
【解析】
【分析】
把这个三角形底边长看作1份,那么等腰三角形的腰为2份,三角形的周长总共为2+2+1(份),它对应的数量为100,用除法求出这个三角形的底边长。
【详解】
100÷(2+2+1)
=100÷5
=20(厘米)
答:这个三角形的底边长20厘米。
【点睛】
此题考查了等腰三角形的性质,注意灵活运用。
27.60°;75°
【解析】
【分析】
根据题意,先利用“∠2比∠1大15°”求∠2的度数:45°+15°=60°;再利用三角形内角和定理:三角形内角和是180°,计算∠3的度数即可。
【详解】
∠2=45°+15°=60°
∠3=180°-45°-60°=75°
答:∠2和∠3的度数分别是60°和75°。
【点睛】
本题考查了三角形内角和定理,关键是掌握三角形内角和为180度。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.用三根小棒围成一个三角形,应选择( )
A.1cm、2cm、3cm B.2cm、3cm、4cm C.4cm、4cm、9cm D.5cm、10cm、20cm
2.如果三角形两条边的长度分别是4cm,7cm,那么第三边不可能是( )
A.10cm B.5cm C.3cm
3.一个三角形中,∠1=50°,∠2=40°.这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形
4.一个平行四边形与一个三角形等底等高,如果把它们的底都扩大2倍,高不变,那么( )
A.它们的面积都不变
B.平行四边形的面积是三角形面积的2倍
C.两个图形的面积相等
D.三角形的面积是平行四边形面积的2倍
5.下图平行线中三个图形的面积( )。
A.都相等 B.三角形面积大 C.梯形面积小 D.平行四边形面积大
二、竖式计算
6.用竖式计算。
三、口算和估算
7.口算.
66+28= 55-38= 80-32=
39+53= 56+24= 63÷3=
21×40= 70×10= 83-57=
四、填空题
8.一个等腰三角形的周长是24 cm,其中一条边长6 cm,那么另外两条边的长分别是( )cm和( )cm.
9.只有一组对边平行的四边形叫做________.
10.一根24厘米长的铁丝,可以围成边长( )厘米的等边三角形,也可以围成边长( )厘米的正方形。
11.猜猜我是什么三角形。
(1)我最大的角是钝角。( )
(2)我有一个角是直角。( )
(3)我有两条边是相等的。( )
(4)我的三条边是相等的。( )
12.一个梯形的上底长2.2厘米,下底长4.8厘米,面积是28平方厘米,它的高是( )厘米.
13.一个等腰三角形的一个底角是55°,这个三角形的顶角是( ),如果它的顶角是20°,那么它的一个底角是( )。
14.在一个三角形中,一条高只有一条对应的底边. .(判断对错)
15.数一数.
(1)
________个
(2)
________个
(3)
________个
(4)
________个
16.在图中,包含的三角形一共有( )个。
五、判断题
17.所有的等边三角形都是等腰三角形。________
18.三根长度分别是6厘米、6厘米、9厘米的小棒能拼成一个等腰三角形. ( )
19.长方形一定是平行四边形,平行四边形也一定是长方形。( )
20.图中共有3条线段、6条射线、1条直线。( )
21.用画垂线的方法可以画长方形或正方形。( )
六、作图题
22.画出每个图形底边上的高.
23.画出下面图形底边上的高。
七、解答题
24.你能想办法求出下边这个六边形的内角和吗?
25.一个平行四边形的一条边延长27厘米后变成了一个梯形,这个梯形的下底是上底的4倍。这个梯形的上底是多少厘米?
26.解决问题。
27.在一个三角形中,∠1,∠2,∠3为三角形的三个角,已知∠1=45°,∠2比∠1大15°,求∠2和∠3的度数分别是多少。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
试题分析:根据“三角形的两边的和一定大于第三边,两边的差一定小于第三边”进行依次分析,选择即可.
解:A、因为1+2=3,所以不能围成三角形;
B、2+3>5,4﹣2<3,所以能围成三角形;
C、4+4=8,所以不能围成三角形;
D、5+10<20,所以不能围成三角形;
故选B.
点评:解答此题应根据三角形的特性,进行分析、解答即可.
2.C
【解析】
【详解】
试题分析:根据三角形的三边关系求得第三边的取值范围,再看哪个选项内的数不在这个范围内即可.
解:设第三边长x.
根据三角形的三边关系,得7﹣4<x<4+7即:3<x<11(但不能取3厘米和11厘米);
因为3厘米不在第三边长的取值范围内,所以不能取.
故选C.
点评:考查三角形的边时,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.
3.A
【解析】
【分析】
三角形内角和是180度.用和减去其中的两个角的度数,就等于第三个角的度数.
【详解】
180-(50+40)
=180-90
=90(度)
是直角三角形
故答案为直角三角形
4.B
【解析】
【分析】
根据平行四边形的面积是与它等底等高的三角形面积的2倍,如果高不变,底都扩大2倍,那么面积也都会扩大2倍,那么平行四边形依然是等底等高的三角形面积的2倍。
【详解】
平行四边形的面积是与它等底等高的三角形面积的2倍,如果高不变,底都扩大2倍,即平行四边形的底还是等于三角形的底,则面积也都会扩大2倍,那么平行四边形依然是等底等高的三角形面积的2倍。
故选B。
【点睛】
此题主要考查的是平行四边形的面积是与它等底等高的三角形面积的2倍。
5.C
【解析】
【分析】
根据平行四边形的面积公式:S=ah,三角形的面积公式:S=ah,梯形的面积公式:S=(a+b)h,把数据分别代入公式求出它们的面积,然后进行比较即可。
【详解】
4×6=24
8×6÷2
=48÷2
=24
(4+2)×6÷2
=6×6÷2
=18
18<24
故答案为:C
【点睛】
此题主要考查平行四边形、三角形、梯形面积公式的灵活运用,关键是熟记公式。
6.9424;21630;7930;12000。
【解析】
【分析】
根据整数乘法的计算方法进行计算即可。
【详解】
124×76=9424 35×618=21630 305×26=7930 50×240=12000
故答案为:9424;21630;7930;12000。
【点睛】
本题考查的是整数乘法计算方法的运用。
7.94;17;48
92;80;21
840;700;26
【解析】
【详解】
略
8. 9 9
【解析】
【详解】
略
9.梯形
【解析】
【详解】
此题可根据梯形的意义来解答,即只有一组对边平行的四边形叫做梯形.
10. 8 6
【解析】
【分析】
等边三角形的三条边相等,等边三角形的边长=周长÷3。正方形的边长=周长÷4,代入数据计算即可。
【详解】
24÷3=8(厘米)
24÷4=6(厘米)
则围成等边三角形,边长为8厘米,围成正方形,边长为6厘米。
【点睛】
解决本题的关键是熟练掌握等边三角形和正方形的周长公式。等边三角形的周长=边长×3,正方形的周长=边长×4。
11. 钝角三角形 直角三角形 等腰三角形 等边三角形
【解析】
【分析】
(1)有一个角是直角的三角形,叫直角三角形;
(2)有一个角是钝角的三角形,叫钝角三角形;
(3)有两条边相等的三角形是等腰三角形;
(4)三条边都相等的三角形是等边三角形(正三角形)。
【详解】
(1)我最大的角是钝角。(钝角三角形)
(2)我有一个角是直角。(直角三角形)
(3)我有两条边是相等的。(等腰三角形)
(4)我的三条边是相等的。(等边三角形)
【点睛】
熟悉三角形的分类标准是解答此题的关键。
12.8
【解析】
略
13. 70° 80°
【解析】
【分析】
等腰三角形中两个底角相等。根据三角形的内角和为180°可知,等腰三角形的顶角=180°-2×底角,底角=(180°-顶角)÷2。据此解答即可。
【详解】
180°-2×55°
=180°-110°
=70°
则这个三角形的顶角是70°。
(180°-20°)÷2
=160°÷2
=80°
则它的一个底角是80°。
【点睛】
本题考查等腰三角形的性质以及三角形的内角和。等腰三角形中,2×底角+顶角=180°。
14.√.
【解析】
【详解】
试题分析:根据三角形高的概念:在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高;则三角形有3个顶点,所以有3条高,据此解答即可.
解:在一个三角形中,一条高只有一条对应的底边.
点评:此题主要考查了三角形高的含义,要灵活运用.
15. 4 4 9 7
【解析】
【详解】
略
16.9
【解析】
【分析】
设最小的正三角形的边长是1,包含A的正三角形的边长可能是1、2、3、4,分类枚举,最后相加得到总数。
【详解】
设最小的正三角形的边长是1;
包含五角星的边长是1的三角形,1个;
包含五角星的边长是2的三角形, 4个;
包含五角星的边长是3的三角形,3个;
包含五角星的边长是4的三角形,1个;
包含五角星的三角形一共有(个)
【点睛】
分类枚举计数是求解几何计数问题最常用的方法,注意在这里三角形有正放和倒放两种情况。
17.√
【解析】
【分析】
三条边都相等的三角形是等边三角形,两条边相等的三角形是等边三角形。三条边相等中包括了两条边相等,所以等腰三角形中包含了等边三角形,等边三角形是特殊的等腰三角形。
【详解】
根据分析可知,等边三角形是特殊的等腰三角形,即所有的等边三角形都是等腰三角形。
故答案为:√。
【点睛】
本题要求熟练掌握等边三角形和等腰三角形的概念,要明白等边三角形一定是等腰三角形,等腰三角形不一定是等边三角形。
18.√
【解析】
【详解】
略
19.×
【解析】
【分析】
长方形是特殊的平行四边形。
【详解】
长方形具有平行四边形的特点,但平行四边形不具有长方形的特点,所以,平行四边形也一定是长方形是错误的。
【点睛】
掌握长方形是特殊的平行四边形是解题的关键,反过来说法不成立。
20.√
【解析】
【详解】
直线没有端点;长度无限;过一点可以画无数条,过两点只能画一条直线。
射线只有一个端点;长度无限。
线段有两个端点,它是直线的一部分;长度有限。
21.√
【解析】
【分析】
根据长方形和正方形的定义进行判断即可。
【详解】
两组对边分别平行、四个角都是直角的四边形叫做长方形。四条边相等、四个角都是直角的四边形叫做正方形。则用画垂线的方法可以画长方形或正方形。
故答案为:√。
【点睛】
正方形和长方形的四个角都是直角。
22.
【解析】
【详解】
试题分析:经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高;在平行四边形中,从一条边上的任意一点向对边作垂线,这点与垂足间的距离叫做以这条边为底的平行四边形的高,平行四边形有无数条高,习惯上作平行四边形的高时都从一个顶点出发作一边的垂线,用三角板的直角可以画出平行四形的高;梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线用三角板的直角可以画出梯形的一条高.
解:
【点评】此题是考查作三角形、平行四边形、梯形的高.注意作高用虚线,并标出垂足.
23.见详解
【解析】
【分析】
(1)从底边相对的顶点作底边的垂线段即为三角形的高。
(2)从底边对边上一点作底边的垂线段即为平行四边形的高。
(3)从下底上一点作上底的垂线段即为梯形的高。
【详解】
【点睛】
本题主要考查学生对作三角形、平行四边形和梯形高的方法的掌握。
24.方法见详解;720°
【解析】
【分析】
如下图,把六边形的一个顶点与其他不相邻的顶点连接起来,这样就把六边形分成4个三角形,4个三角形的内角和等于六边形的内角和,据此即可解答。
【详解】
如上图,把六边形分成4个三角形,三角形的内角和等于180°。
180°×4=720°
答:六边形的内角和等于720°。
【点睛】
本题主要考查学生观察和分析问题的能力。
25.9厘米
【解析】
【分析】
梯形的下底是上底的4倍,所以下底比上底多3倍,据此求解。
【详解】
27÷(4-1) =9(厘米)
答:这个梯形的上底是9厘米。
【点睛】
简单的差倍问题,较小数=差÷(倍数-1)。
26.20厘米
【解析】
【分析】
把这个三角形底边长看作1份,那么等腰三角形的腰为2份,三角形的周长总共为2+2+1(份),它对应的数量为100,用除法求出这个三角形的底边长。
【详解】
100÷(2+2+1)
=100÷5
=20(厘米)
答:这个三角形的底边长20厘米。
【点睛】
此题考查了等腰三角形的性质,注意灵活运用。
27.60°;75°
【解析】
【分析】
根据题意,先利用“∠2比∠1大15°”求∠2的度数:45°+15°=60°;再利用三角形内角和定理:三角形内角和是180°,计算∠3的度数即可。
【详解】
∠2=45°+15°=60°
∠3=180°-45°-60°=75°
答:∠2和∠3的度数分别是60°和75°。
【点睛】
本题考查了三角形内角和定理,关键是掌握三角形内角和为180度。
答案第1页,共2页
答案第1页,共2页
