华东师大版七年级下册数学 9.2 多边形的内角和与外角和 课件(共28张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 9.2 多边形的内角和与外角和 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 09:45:25 | ||
图片预览





文档简介
(共28张PPT)
§9.2多边形的内角和与外角和
(第一课时)
南靖县靖城中学
陈小英
培训对象:七年(1)班
培训老师:陈小英
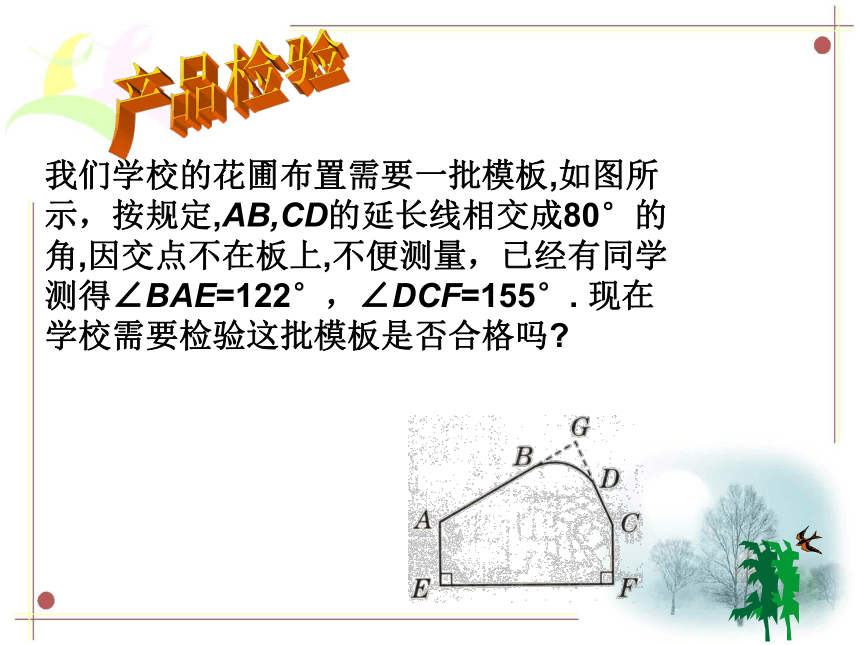
我们学校的花圃布置需要一批模板,如图所示,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,已经有同学测得∠BAE=122°,∠DCF=155°. 现在学校需要检验这批模板是否合格吗
1.什么叫三角形
三角形是由三条不在同一条直线上的
线段首尾顺次连结组成的平面图形
2.三角形的内角和是多少?
你能说出什么叫四边形、五边形、多边形(也就是n边形)吗?
由n条不在同一直线上的线段首尾顺次连结组成的平面图形,称为n边形。
又称为多边形。
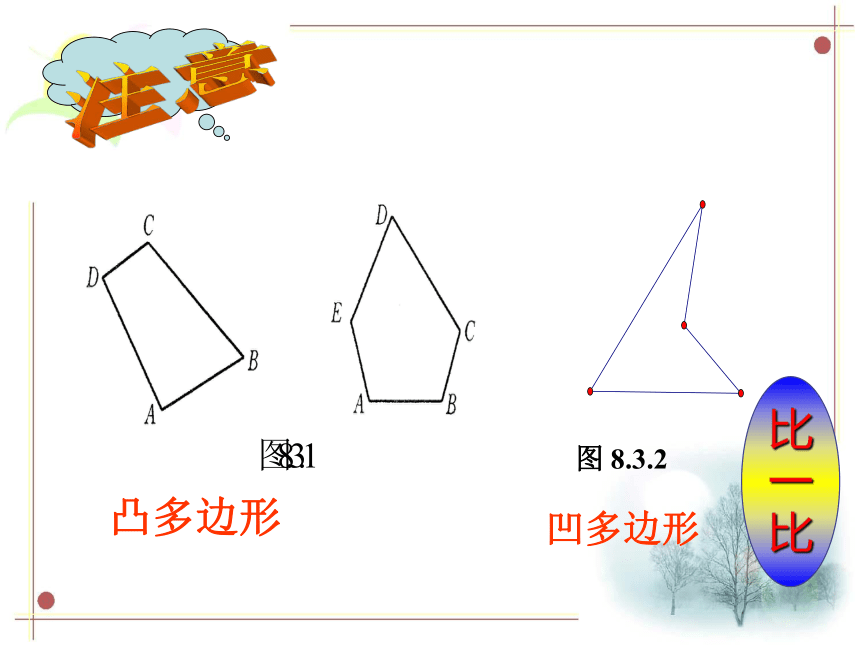
图 8.3.2
比
一
比
凸多边形
凹多边形
1、什么叫正三角形?什么叫正方形?
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
2、什么叫正多边形?
归纳:
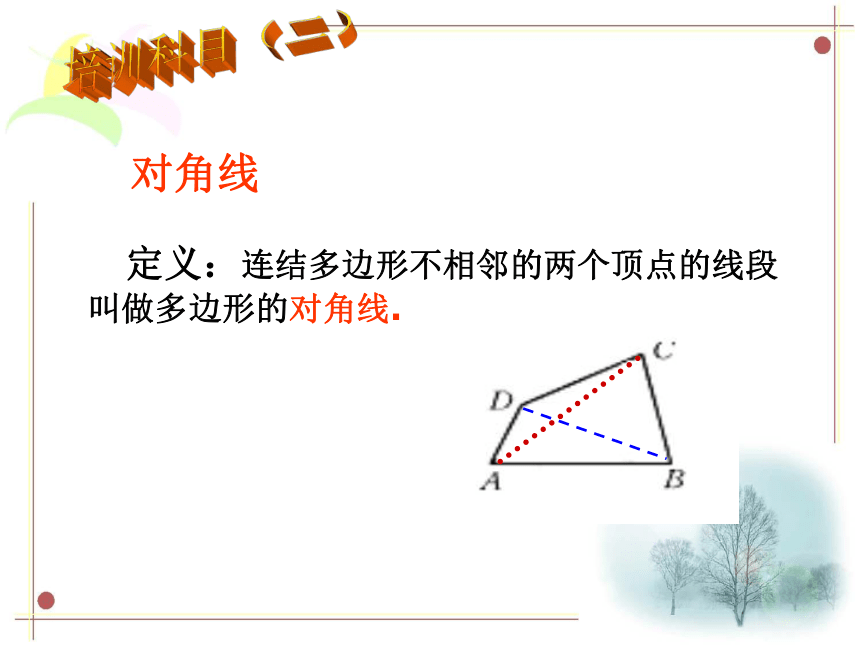
定义:连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
对角线
请大家思考:五边形ABCDE共有几条对角线呢?
五边形ABCDE共有5条对角线。
C
请大家思考:六边形ABCDEF共有几条对角线呢?
六边形ABCDEF共有9条对角线。
有没有什么
规律呢?
四边形从一个顶点出发,能引出 条对角线?
五边形从一个顶点出发,能引出 条对角线?
六边形从一个顶点出发,能引出 条对角线?
n边形从一个顶点出发,能引出 条对角线?
1
2
3
(n-3)
想一想
C
n边形一共有 条对角线
1、八边形有 条对角线。
2、一个多边形从一个顶点出发可以画8条对角线,那么这个多边形是 边形。
试试你的身手
数学的
基本思想
化未知为已知
探究: n边形(多边形)的内角和是多少?
由特殊到一般
多边形的边数 3 4 5 6 7 ..... n
分成的三角形的个数 1
多边形的内角和 180°
探究:多边形(n边形)的内角和是多少?
3
4
5
n-2
540 °
720 °
900 °
180 ° (n-2)
探究:多边形(n边形)的内角和是多少?
请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?
3
4
5
n-2
540 °
720 °
900 °
180 ° (n-2)
试试你的身手
例1.求七边形的内角和的度数.
例2.已知多边形的内角和的度数为720°,则这个多边形的边数为________
原来这么简单
今天的培训你学到了什么知识?你能用自己的话说说吗?
化未知为已知
从特殊到一般
第一关
1、五边形的内角和等于_____。
2 、如果一个多边形的边数增加1,则这个多边形的内角和( )
A 、不变 B 、减少180 °C 、增加180 ° D 、无法确定
540 °
C
如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员已经测得∠BAE=122°,∠DCF=155°.你能判断模板是否合格吗 为什么
第二关
第三关
有一个多边形, 从它的一个顶点出发共可作9条对角线,请质检员算出这个多边形的内角和。
科学的探讨研究,其本身就含有至美,其本身给人的愉快就是报酬。
——(波兰科学家)居里夫人
A组:课本第86页练习1、2;
B组:思考题
“多边形的内角和公式”的得出还有其他的办法吗?
§9.2多边形的内角和与外角和
(第一课时)
南靖县靖城中学
陈小英
培训对象:七年(1)班
培训老师:陈小英
我们学校的花圃布置需要一批模板,如图所示,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,已经有同学测得∠BAE=122°,∠DCF=155°. 现在学校需要检验这批模板是否合格吗
1.什么叫三角形
三角形是由三条不在同一条直线上的
线段首尾顺次连结组成的平面图形
2.三角形的内角和是多少?
你能说出什么叫四边形、五边形、多边形(也就是n边形)吗?
由n条不在同一直线上的线段首尾顺次连结组成的平面图形,称为n边形。
又称为多边形。
图 8.3.2
比
一
比
凸多边形
凹多边形
1、什么叫正三角形?什么叫正方形?
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
2、什么叫正多边形?
归纳:
定义:连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
对角线
请大家思考:五边形ABCDE共有几条对角线呢?
五边形ABCDE共有5条对角线。
C
请大家思考:六边形ABCDEF共有几条对角线呢?
六边形ABCDEF共有9条对角线。
有没有什么
规律呢?
四边形从一个顶点出发,能引出 条对角线?
五边形从一个顶点出发,能引出 条对角线?
六边形从一个顶点出发,能引出 条对角线?
n边形从一个顶点出发,能引出 条对角线?
1
2
3
(n-3)
想一想
C
n边形一共有 条对角线
1、八边形有 条对角线。
2、一个多边形从一个顶点出发可以画8条对角线,那么这个多边形是 边形。
试试你的身手
数学的
基本思想
化未知为已知
探究: n边形(多边形)的内角和是多少?
由特殊到一般
多边形的边数 3 4 5 6 7 ..... n
分成的三角形的个数 1
多边形的内角和 180°
探究:多边形(n边形)的内角和是多少?
3
4
5
n-2
540 °
720 °
900 °
180 ° (n-2)
探究:多边形(n边形)的内角和是多少?
请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?
3
4
5
n-2
540 °
720 °
900 °
180 ° (n-2)
试试你的身手
例1.求七边形的内角和的度数.
例2.已知多边形的内角和的度数为720°,则这个多边形的边数为________
原来这么简单
今天的培训你学到了什么知识?你能用自己的话说说吗?
化未知为已知
从特殊到一般
第一关
1、五边形的内角和等于_____。
2 、如果一个多边形的边数增加1,则这个多边形的内角和( )
A 、不变 B 、减少180 °C 、增加180 ° D 、无法确定
540 °
C
如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员已经测得∠BAE=122°,∠DCF=155°.你能判断模板是否合格吗 为什么
第二关
第三关
有一个多边形, 从它的一个顶点出发共可作9条对角线,请质检员算出这个多边形的内角和。
科学的探讨研究,其本身就含有至美,其本身给人的愉快就是报酬。
——(波兰科学家)居里夫人
A组:课本第86页练习1、2;
B组:思考题
“多边形的内角和公式”的得出还有其他的办法吗?
