人教版初中数学七年级下册第十章数据的收集、整理与描述专项训练试题:精品试卷(word版 含解析)
文档属性
| 名称 | 人教版初中数学七年级下册第十章数据的收集、整理与描述专项训练试题:精品试卷(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 328.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 09:57:09 | ||
图片预览



文档简介
初中数学七年级下册第十章数据的收集、整理与描述专项训练
(2021-2022学年 考试时间:90分钟,总分100分)
班级:__________ 姓名:__________ 总分:__________
题号 一 二 三
得分
一、单选题(10小题,每小题3分,共计30分)
1、某运动品牌经销商对鞋码大小进行抽样调查,经销商最感兴趣的数据是( )
A.中位数 B.平均数 C.众数 D.方差
2、下列说法中正确的个数是( )个.
①a表示负数;
②若|x|=x,则x为正数;
③单项式的系数是;
④多项式﹣3a2b+7a2b2﹣2ab﹣1的次数是4;
⑤了解全市中小学生每天的零花钱适合抽样调查;
⑥调查七年级(1)班学生的某次数学考试成绩适合抽样调查.
A.1 B.2 C.3 D.4
3、下列调查中,最适合采用抽样调查的是( )
A.调查一批防疫口罩的质量
B.调查某校九年级学生的视力
C.对乘坐某班次飞机的乘客进行安检
D.国务院于2020年11月1日开展的第七次全国人口调查
4、在一个样本中,40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是6,5,15,7,则第4小组的频数是( )
A.7 B.8 C.9 D.10
5、下图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在小组,而不在小组),根据图形提供的信息,下列说法中错误的是( )
A.该学校教职工总人数是50人
B.年龄在小组的教职工人数占总人数的20%
C.某教师40岁,则全校恰有10名教职工比他年轻
D.教职工年龄分布最集中的在这一组
6、某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的期中数学成绩进行了统计,下面判断中不正确的有( )
A.这种调查的方式是抽样调查 B.800名学生是总体
C.每名学生的期中数学成绩是个体 D.100名学生的期中数学成绩是总体的一个样本
7、为了了解某校七年级名学生的跳绳情况(秒跳绳的次数),随机对该年级名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数为:,则以下说法正确的是( )
A.跳绳次数不少于次的占
B.大多数学生跳绳次数在范围内
C.跳绳次数最多的是次
D.由样本可以估计全年级人中跳绳次数在次的大约有人
8、下列调查中,适合用普查方式的是( )
A.调查佛山市市民的吸烟情况
B.调查佛山市电视台某节目的收视率
C.调查佛山市市民家庭日常生活支出情况
D.调查佛山市某校某班学生对“文明佛山”的知晓率
9、下列调查中,最适合采用全面调查方式的是( )
A.了解外地游客对岳飞庙的印象 B.了解一批圆珠笔的寿命
C.了解某班学生的身高情况 D.了解人们保护海洋的意识
10、下列调查中,适合采用全面调查的是( )
A.了解一批电灯泡的使用寿命 B.调查榆林市中学生的视力情况
C.了解榆林市居民节约用水的情况 D.调查“天问一号”火星探测器零部件的的质量
二、填空题(5小题,每小题4分,共计20分)
1、开学之初,七(1)班的张老师为了安排座位,需要了解全班同学的视力情况,你认为张老师应采取_________(填“全面调查”或“抽样调查”)的统计方法较为合适.
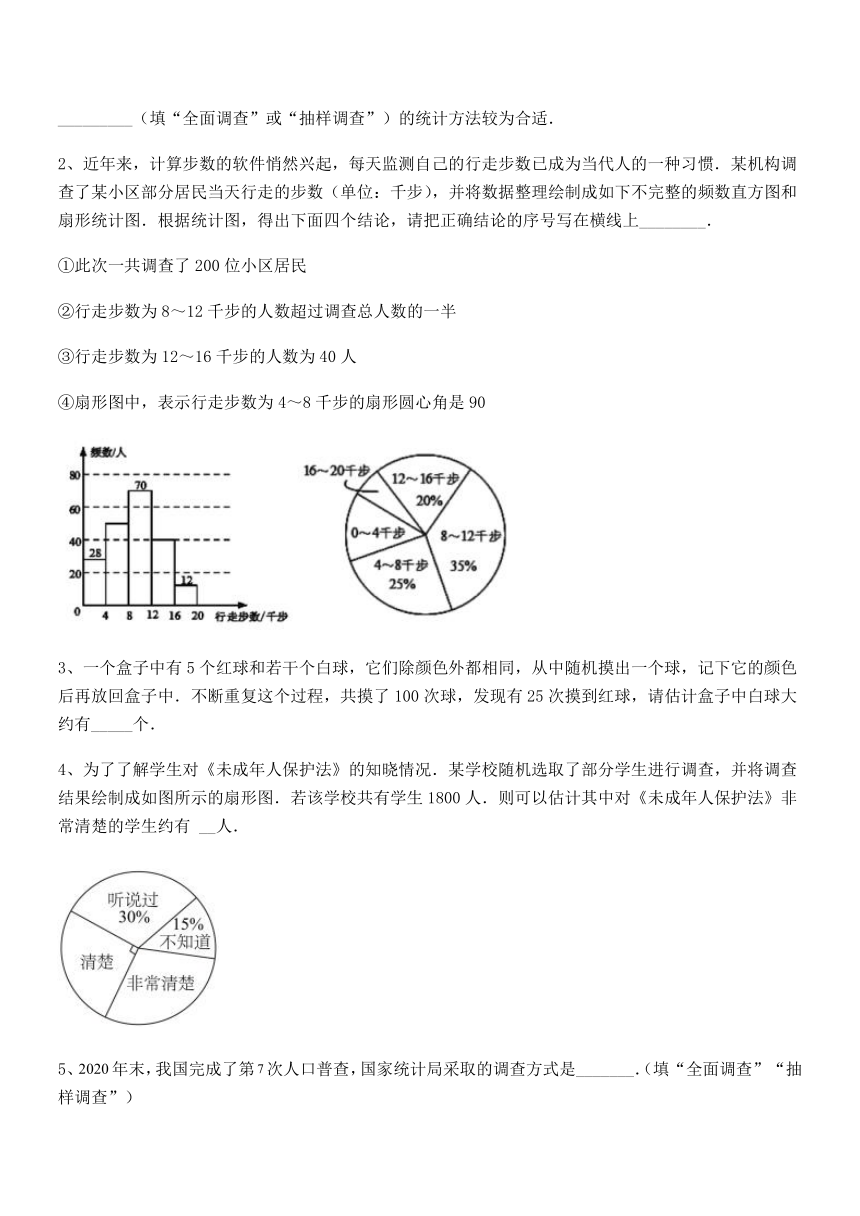
2、近年来,计算步数的软件悄然兴起,每天监测自己的行走步数已成为当代人的一种习惯.某机构调查了某小区部分居民当天行走的步数(单位:千步),并将数据整理绘制成如下不完整的频数直方图和扇形统计图.根据统计图,得出下面四个结论,请把正确结论的序号写在横线上________.
①此次一共调查了200位小区居民
②行走步数为8~12千步的人数超过调查总人数的一半
③行走步数为12~16千步的人数为40人
④扇形图中,表示行走步数为4~8千步的扇形圆心角是90
3、一个盒子中有5个红球和若干个白球,它们除颜色外都相同,从中随机摸出一个球,记下它的颜色后再放回盒子中.不断重复这个过程,共摸了100次球,发现有25次摸到红球,请估计盒子中白球大约有_____个.
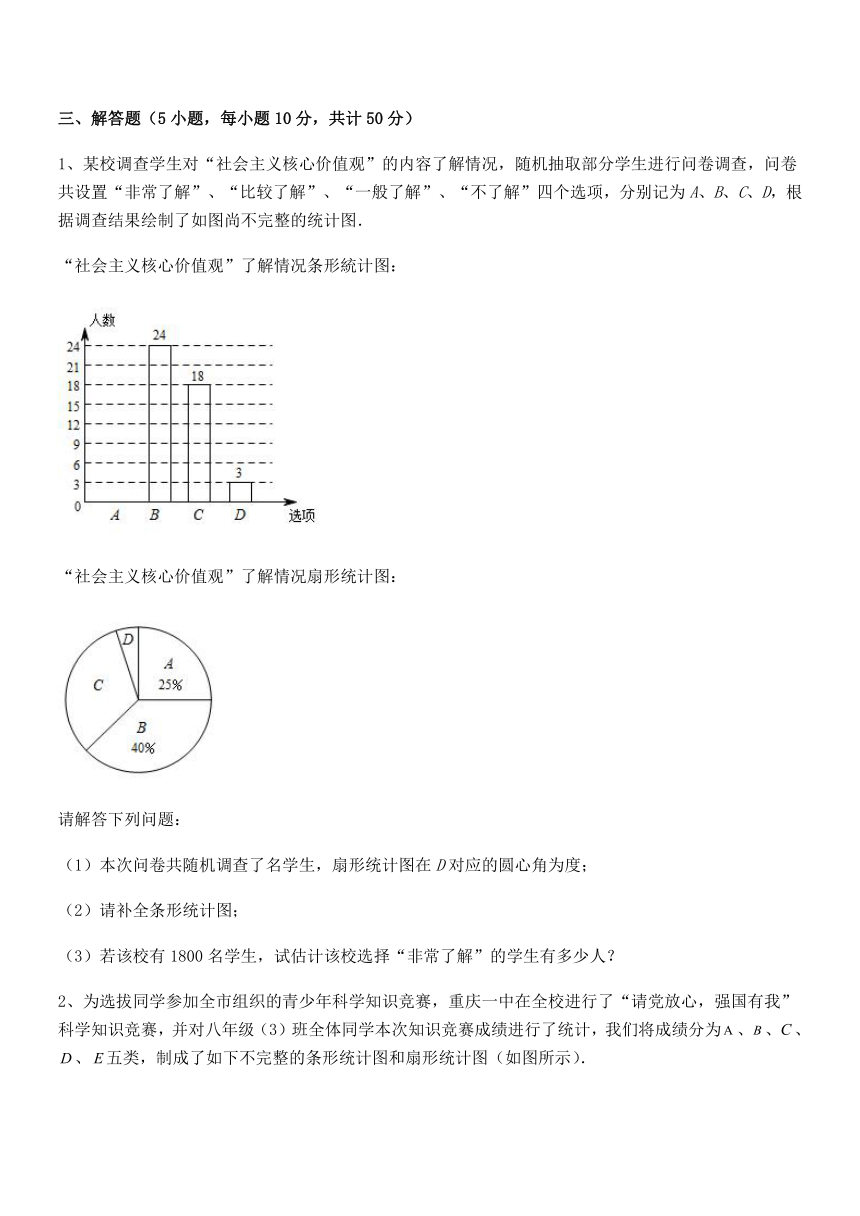
4、为了了解学生对《未成年人保护法》的知晓情况.某学校随机选取了部分学生进行调查,并将调查结果绘制成如图所示的扇形图.若该学校共有学生1800人.则可以估计其中对《未成年人保护法》非常清楚的学生约有 __人.
5、年末,我国完成了第次人口普查,国家统计局采取的调查方式是_______.(填“全面调查”“抽样调查”)
三、解答题(5小题,每小题10分,共计50分)
1、某校调查学生对“社会主义核心价值观”的内容了解情况,随机抽取部分学生进行问卷调查,问卷共设置“非常了解”、“比较了解”、“一般了解”、“不了解”四个选项,分别记为A、B、C、D,根据调查结果绘制了如图尚不完整的统计图.
“社会主义核心价值观”了解情况条形統计图:
“社会主义核心价值观”了解情况扇形统计图:
请解答下列问题:
(1)本次问卷共随机调查了名学生,扇形统计图在D对应的圆心角为度;
(2)请补全条形统计图;
(3)若该校有1800名学生,试估计该校选择“非常了解”的学生有多少人?
2、为选拔同学参加全市组织的青少年科学知识竞赛,重庆一中在全校进行了“请党放心,强国有我”科学知识竞赛,并对八年级(3)班全体同学本次知识竞赛成绩进行了统计,我们将成绩分为、、、、五类,制成了如下不完整的条形统计图和扇形统计图(如图所示).
请你根据统计图中的信息,解答下列问题:
(1)八年级(3)班学生总人数是__________人;在扇形统计图中,的值是__________;
(2)若八年级(3)班得等级的同学人数是得等级的同学人数的4倍,请将条形统计图补充完整;
(3)若等级为表示优秀,等级为表示良好,等级为表示合格,等级为表示不合格,等级为表示差,根据本次统计结果,估计全校2000名学生中知识竞赛成绩在合格及以上的学生大约有多少人?
3、为了解地铁开通对节约“出行时间”影响情况,对地铁1号线上某趟列车上的部分乘客进行随机抽样调查.将调查结果分为、、、四类,其中表示“出行节约0﹣10分钟”,表示“出行节约10﹣30分钟”,表示“出行节约30分钟以上”,表示“其他情况”,并根据调查结果绘制了图①、图②这两个不完整的统计图表.
(1)求这次调查的总人数.
(2)补全条形统计图.
(3)在图②的扇形统计图中,求类所对应的扇形圆心角的度数.
4、为了了解某地区60~75岁的老年人的锻炼情况,利用公安机关户籍网,随机电话调查了该区60~75岁的300名老人平均每天的锻炼时间,整理得到下面的表格:
平均每天锻炼时间 人数 占被调查数的百分比
男 女 合计
1h以内(含1h) 43 83 126 42%
1-2h(含2h) 20 28 48 16%
2h以上 7 5 12 4%
不参加锻炼 77 37 114 38%
合计 147 153 300 100%
(1)男性老年人参加锻炼的人数有________人,女性老年人参加锻炼的人数有________人,老年人中,参加锻炼的占被调查者的________%;
(2)不参加锻炼的老年人中,男性大约是女性的几倍?
(3)根据此表数据分析,你对该区老年人的锻炼情况有什么建议吗?
(4)对本题的课题进行调查时,如果清晨到公园或市人民广场询问300名老年人,或在某居民小区调查10名老年人,你认为这样得到的数据,可以作为调查分析、得出结论的依据吗?请说明理由.
5、为提升学生的艺术素养,学校计划开设四门艺术选修课:A:书法;B,绘画;C,乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),将数据进行整理,并绘制成如图两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)木次调查的学生共有 人,扇形统计图中∠α的度数是 ;
(2)请把条形统计图补充完整.
---------参考答案-----------
一、单选题
1、C
【解析】
【分析】
经销商最感兴趣的是这组鞋号中销售量最大的尺码,即这组鞋号的众数.
【详解】
解:由于众数是数据中出现次数最多的数.经销商最感兴趣的是这组鞋号中销售量最大的尺码,故应关注众数的大小.
故选:C.
【点睛】
本题主要考查学生对统计量的意义的理解与运用,要求学生对统计量进行合理的选择和恰当的运用.
2、B
【解析】
【分析】
直接根据单项式以及多项式的相关概念,正数和负数,抽样调查和全面调查的概念进行判断即可.
【详解】
解:①a表示一个正数、0或者负数,故原说法不正确;
②若|x|=x,则x为正数或0,故原说法不正确;
③单项式﹣的系数是﹣,故原说法不正确;
④多项式﹣3a2b+7a2b2﹣2ab﹣1的次数是4,故原说法正确;
⑤了解全市中小学生每天的零花钱适合抽样调查,故原说法正确;
⑥调查七年级(1)班学生的某次数学考试成绩适合全面调查,故原说法不正确.
正确的个数为2个,
故选:B.
【点睛】
本题考查了多项式、正数和负数、抽样调查和全面调查及绝对值的性质,掌握它们的性质概念是解本题的关键.
3、A
【解析】
【分析】
根据抽样调查和普查的定义进行求解即可.
【详解】
解:A.调查一批防疫口罩的质量,适合抽样调查,故选项符合题意;
B.调查某校九年级学生的视力,适合全面调查,故选项不符合题意;
C.对乘坐某班次飞机的乘客进行安检,适合全面调查,故选项不符合题意;
D.国务院于2020年11月1日开展的第七次全国人口调查,适合全面调查,故选项不符合题意;
故选A.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4、A
【解析】
【分析】
每组的数据个数就是每组的频数,40减去第1,2,3,5小组数据的个数就是第4组的频数.
【详解】
解:第4小组的频数是40 (6+5+15+7)=7,
故选:A.
【点睛】
本题考查频数和频率的知识,注意掌握每个小组的频数等于数据总数减去其余小组的频数,即各小组频数之和等于数据总和.
5、C
【解析】
【分析】
各组的频数的和就是总人数,再根据百分比、众数、中位数的定义逐一解题.
【详解】
解:A. 该学校教职工总人数是4+6+11+10+9+6+4=50人,正确,故A不符合题意;
B. 年龄在小组的教职工人数占总人数的20%,正确,故B不符合题意;
C. 教职工年龄的中位数在这一组,某教师40岁,则全校恰有10名教职工比他年轻说法是错误的,故C符合题意;
D. 教职工年龄分布最集中的在这一组,正确,故D不符合题意,
故选:C.
【点睛】
本题考查频数分布直方图,是重要考点,从图中获取正确信息是解题关键.
6、B
【解析】
【分析】
总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体.本题考查的对象是七年级800名学生期中数学考试情,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本.
【详解】
解:A、题中的调查方式为抽样调查,选项正确,不符合题意;
B、总体为800名学生的期中数学成绩,而不是学生,选项错误,符合题意;
C、每名学生的期中数学成绩是个体,选项正确,不符合题意;
D、100名学生的期中数学成绩是总体的一个样本,选项正确,不符合题意;
故选B
【点睛】
本题主要考查了总体、个体与样本,解题要分清具体问题中的总体、个体与样本.关键是明确考查的对象,总体、个体与样本的考察对象是相同的,所不同的是范围的大小.
7、A
【解析】
【分析】
根据频数发布直方图,跳绳次数不少于100次的人数相加除总人数后再乘即可得;由频数分布直方图可知,大多数学生跳绳次数在范围内;因为每组数据包括左端值不包括右端值,所以跳绳次数最多的不是次;由样本可以估计全年级人中跳绳次数在次的大约有(人),进行判断即可得.
【详解】
A、跳绳次数不少于次的占,选项说法正确,符合题意;
B、由频数分布直方图可知,大多数学生跳绳次数在范围内,选项说法错误,不符合题意;
C、每组数据包括左端值不包括右端值,故跳绳次数最多的不是次,选项说法错误,不符合题意;
D、由样本可以估计全年级人中跳绳次数在次的大约有(人),选项说法错误,不符合题意;
故选A.
【点睛】
本题考查了频数(率)分布直方图,解题的关键是能够根据频数(率)分布直方图所给的信息进行求解.
8、D
【解析】
【分析】
根据普查和抽样调查的定义进行逐一判断即可.
【详解】
解:A、调查佛山市市民的吸烟情况,应采用抽样调查,故此选项不符合题意;
B、调查佛山市电视台某节目的收视率,应采用抽样调查,故此选项不符合题意;
C、调查佛山市市民家庭日常生活支出情况,应采用抽样调查,故此选项不符合题意;
D、调查佛山市某校某班学生对“文明佛山”的知晓率,应采用普查,故此选项符合题意;
故选D.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
9、C
【解析】
【分析】
根据全面调查与抽样调查的意义,结合具体的问题情境进行判断即可.
【详解】
解:A.了解外地游客对岳飞庙的印象,可采取抽样调查,因此选项A不符合题意;
B.了解一批圆珠笔的寿命,可采取抽样调查,因此选项B不符合题意;
C.了解某班学生的身高情况,可采用全面调查,因此选项C符合题意;
D.了解人们保护海洋的意识,可采取抽样调查,因此选项D不符合题意;
故选:C.
【点睛】
本题考查全面调查与抽样调查,理解全面调查与抽样调查的意义和适用的具体问题情境是正确判断的关键.
10、D
【解析】
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,再逐一分析即可.
【详解】
解:A.了解一批电灯泡的使用寿命,具有破坏性,适合抽样调查,不符合题意;
B.调查榆林市中学生的视力情况,适合抽样调查,不符合题意;
C.了解榆林市居民节约用水的情况,适合抽样调查,不符合题意;
D.调查“天问一号”火星探测器零部件的的质量,必需采用全面调查,符合题意;
故选:D.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
二、填空题
1、全面调查
【解析】
【分析】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
【详解】
解:因为要了解全班同学的视力情况范围较小、难度不大,所以应采取全面调查的方法比较合适.
故答案为:全面调查.
【点睛】
本题考查的是调查方法的选择;正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析.
2、①③④
【解析】
【分析】
对每个选项的问题逐一计算,加以甄别即可.
【详解】
解:本次调查的总人数为(人).
∴①正确;
∵行走步数为8~12千步的人数为70人,而调查的总人数为200人,没有超过一半
∴②错误;
∵行走步数为12~16千步的人数为(人).
∴③选项正确;
行走步数为4~8千步的扇形的圆心角为.
∴④正确.
故答案为:①③④.
【点睛】
本题考查了统计调查等知识点,熟知各种算法是解题的基础,从统计图中提取相关的对应数据是解题的关键.
3、15
【解析】
【分析】
由共摸了100次球,发现有25次摸到红球知摸到红球的概率为0.25,设盒子中白球有个,可得,解之即可.
【详解】
解:设盒子中白球大约有个,
根据题意,得:,
解得,
经检验是分式方程的解,
所以估计盒子中白球大约有15个,
故答案为:15.
【点睛】
本题考查用样本估计总体,从一个总体得到一个包含大量数据的样本,我们很难从一个个数字中直接看出样本所包含的信息,解题的关键是用频率分布直方图来表示相应样本的频率分布,从而去估计总体的分布情况.
4、540
【解析】
【分析】
先求出非常清楚所占的百分比,再乘以该校的总人数,即可得出答案.
【详解】
解:根据题意得:
(人.
答:可以估计其中对《未成年人保护法》非常清楚的学生约有540人.
故答案为:540.
【点睛】
此题考查了用样本估计总体,在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
5、全面调查
【解析】
【分析】
根据全面调查和抽样调查的概念判断即可.
【详解】
解:为了全面的、可靠的得到我国人口信息,
所以国家统计局采取的调查方式是全面调查,
故答案为:全面调查.
【点睛】
本题考查的是全面调查和抽样调查,解题的关键是掌握通过普查可以直接得到较为全面、可靠的信息,但花费的时间较长,耗费大,且一些调查项目并不适合普查.其一,调查者能力有限,不能进行普查,其二,调查过程带有破坏性,其三,有些被调查的对象无法进行普查.
三、解答题
1、(1)60,18;(2)15,补图见解答;(3)450.
【分析】
(1)“B比较了解”的有24人,占调查人数的40%,可求出调查人数,进而求出“D一般了解”所占的百分比,进而计算其相应的圆心角的度数,
(2)求出“A非常了解”的人数,即可补全条形统计图;
(3)用该校的总人数乘以“非常了解”的人数所占的百分比即可.
【详解】
解:(1)本次问卷共随机调查的学生数是:24÷40%=60(名),
扇形统计图中D对应的圆心角为360°×=18°,
故答案为:60,18;
(2)60×25%=15(人),
补全条形统计图如图所示:
(3)1800×=450(人),
答:估计该校选择“非常了解”的学生有450人.
【点睛】
本题考查扇形统计图、条形统计图的意义和制作方法,从两个统计图中获取数量和数量关系是正确解答的关键.
2、(1)50;20;(2)补全条形见祥解;(3)全校2000名学生中知识竞赛成绩在合格及以上的学生大约有1440人.
【分析】
(1)先从条形图统计类人数为12人,从扇形统计图中B类人数所占百分比为24%,再求八年级(3)班学生总人数是12÷24%=50人,再求出D类的百分比即可;
(2)根据C等级的同学人数是得等级的同学人数的4倍,设等级的同学人数为x人,则等级的同学人数为4x人,列出方程x+4x=50-8-12-10,求解即可;
(3)先求出八年级(3)班知识竞赛成绩在合格及以上的学生大有8+12+16=36人,再求出占班级人数的百分比为36÷50×100%=72%,然后利用样本的百分比含量估计全校2000名学生中知识竞赛成绩在合格及以上的学生大约有2000×72%=1440人即可.
【详解】
解:(1)八年级(3)班全体同学本次知识竞赛成绩从条形图统计类人数为12人,从扇形统计图中B类人数所占百分比为24%,
∴八年级(3)班学生总人数是12÷24%=50人
∴10÷50×100%=20%,
∴a=20,
故答案为50;20;
(2)∵等级的同学人数是得等级的同学人数的4倍
设等级的同学人数为x人,则等级的同学人数为4x人,
∴x+4x=50-8-12-10,
∴x=4;
补全条形图如下
(3)八年级(3)班知识竞赛成绩在合格及以上的学生大有8+12+16=36人,占班级人数的百分比为36÷50×100%=72%,
∴全校2000名学生中知识竞赛成绩在合格及以上的学生大约有2000×72%=1440人.
【点睛】
本题考查样本的容量,从条形图与扇形图获取信息,补画条形统计图,用样本的百分比含量估计总体中的数量,掌握样本的容量的求法,从条形图与扇形图获取信息,补画条形统计图,用样本的百分比含量估计总体中的数量是解题关键.
3、(1)50人;(2)见解析;(3)108°
【分析】
(1)利用类的人数除以类所占百分比,即可求解;
(2)求出“出行节约30分钟以上”的人数,即可求解;
(3)用360°乘以类所占的百分比,即可求解.
【详解】
解:(1)调查的总人数是:(人).
(2)“出行节约30分钟以上”的人数有 (人),
补全图形,如图所示:
(3)A类所对应的扇形圆心角的度数是.
【点睛】
本题主要考查了条形统计图和扇形统计图,明确题意,准确获取信息是解题的关键.
4、(1)70,116,62;(2)2倍;(3)要增强该地区老年人“生命在于运动”的观念;(4)不可以,理由见解析
【分析】
(1)观察表格可得出男性老年人和女性老年人参加锻炼的人数,由此进行解答;
(2)由表格可知不参加锻炼的老年人中,其中男性有77人,女性有37人,进而可得到男性人数和女性人数的倍数关系;
(3)此题答案不唯一,根据图表分析参加锻炼的人数不太多,可以就注重锻炼来分析;
(4)可以根据抽样调查中样本的代表性进行解答.
【详解】
解: (1)男性老年人参加锻炼的人数有43+20+7=70(人),女性参加锻炼的人数有83+28+5=116(人);老年人中,参加锻炼的占被调查者的.
(2)不参加锻炼的老年人中,其中男性有77人,女性有37人,故男性大约是女性的2倍.
(3)根据此表数据分析:不参加锻炼的老年人约占38%,可见该地区的老年人锻炼意识不强,尤其是男性老年人,只有半数的男性老年人参加锻炼,所以要增强该地区老年人“生命在于运动”的观念.
(4)不可以,因为,清晨到公园或市民广场的老年人都是注意锻炼的老年人,不能代表该区所有的老年入的锻炼情况,不具有广泛的代表性,即样本不具有代表性、广泛性,故这种调查方法得出的结论不符合实际.
【点睛】
本题考查抽样调查的知识,解题的关键是对表格进行正确分析进而得到答案.
5、(1);(2)画图见解析
【分析】
(1)由B组8人,占比20%,列式可得总人数,由C组的占比乘以可得圆心角的度数;
(2)先计算出C组的人数,再补全图形即可.
【详解】
解:(1)由B组8人,占比20%,可得总人数为:人,
所以C组所在扇形的圆心角为:
故答案为:
(2)C组的人数为:人,
补全图形如下:
【点睛】
本题考查的是从扇形图与条形图中获取信息,频数与频率,画条形统计图,计算扇形某部分的圆心角,掌握以上基础知识是解题的关键.
(2021-2022学年 考试时间:90分钟,总分100分)
班级:__________ 姓名:__________ 总分:__________
题号 一 二 三
得分
一、单选题(10小题,每小题3分,共计30分)
1、某运动品牌经销商对鞋码大小进行抽样调查,经销商最感兴趣的数据是( )
A.中位数 B.平均数 C.众数 D.方差
2、下列说法中正确的个数是( )个.
①a表示负数;
②若|x|=x,则x为正数;
③单项式的系数是;
④多项式﹣3a2b+7a2b2﹣2ab﹣1的次数是4;
⑤了解全市中小学生每天的零花钱适合抽样调查;
⑥调查七年级(1)班学生的某次数学考试成绩适合抽样调查.
A.1 B.2 C.3 D.4
3、下列调查中,最适合采用抽样调查的是( )
A.调查一批防疫口罩的质量
B.调查某校九年级学生的视力
C.对乘坐某班次飞机的乘客进行安检
D.国务院于2020年11月1日开展的第七次全国人口调查
4、在一个样本中,40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是6,5,15,7,则第4小组的频数是( )
A.7 B.8 C.9 D.10
5、下图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在小组,而不在小组),根据图形提供的信息,下列说法中错误的是( )
A.该学校教职工总人数是50人
B.年龄在小组的教职工人数占总人数的20%
C.某教师40岁,则全校恰有10名教职工比他年轻
D.教职工年龄分布最集中的在这一组
6、某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的期中数学成绩进行了统计,下面判断中不正确的有( )
A.这种调查的方式是抽样调查 B.800名学生是总体
C.每名学生的期中数学成绩是个体 D.100名学生的期中数学成绩是总体的一个样本
7、为了了解某校七年级名学生的跳绳情况(秒跳绳的次数),随机对该年级名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数为:,则以下说法正确的是( )
A.跳绳次数不少于次的占
B.大多数学生跳绳次数在范围内
C.跳绳次数最多的是次
D.由样本可以估计全年级人中跳绳次数在次的大约有人
8、下列调查中,适合用普查方式的是( )
A.调查佛山市市民的吸烟情况
B.调查佛山市电视台某节目的收视率
C.调查佛山市市民家庭日常生活支出情况
D.调查佛山市某校某班学生对“文明佛山”的知晓率
9、下列调查中,最适合采用全面调查方式的是( )
A.了解外地游客对岳飞庙的印象 B.了解一批圆珠笔的寿命
C.了解某班学生的身高情况 D.了解人们保护海洋的意识
10、下列调查中,适合采用全面调查的是( )
A.了解一批电灯泡的使用寿命 B.调查榆林市中学生的视力情况
C.了解榆林市居民节约用水的情况 D.调查“天问一号”火星探测器零部件的的质量
二、填空题(5小题,每小题4分,共计20分)
1、开学之初,七(1)班的张老师为了安排座位,需要了解全班同学的视力情况,你认为张老师应采取_________(填“全面调查”或“抽样调查”)的统计方法较为合适.
2、近年来,计算步数的软件悄然兴起,每天监测自己的行走步数已成为当代人的一种习惯.某机构调查了某小区部分居民当天行走的步数(单位:千步),并将数据整理绘制成如下不完整的频数直方图和扇形统计图.根据统计图,得出下面四个结论,请把正确结论的序号写在横线上________.
①此次一共调查了200位小区居民
②行走步数为8~12千步的人数超过调查总人数的一半
③行走步数为12~16千步的人数为40人
④扇形图中,表示行走步数为4~8千步的扇形圆心角是90
3、一个盒子中有5个红球和若干个白球,它们除颜色外都相同,从中随机摸出一个球,记下它的颜色后再放回盒子中.不断重复这个过程,共摸了100次球,发现有25次摸到红球,请估计盒子中白球大约有_____个.
4、为了了解学生对《未成年人保护法》的知晓情况.某学校随机选取了部分学生进行调查,并将调查结果绘制成如图所示的扇形图.若该学校共有学生1800人.则可以估计其中对《未成年人保护法》非常清楚的学生约有 __人.
5、年末,我国完成了第次人口普查,国家统计局采取的调查方式是_______.(填“全面调查”“抽样调查”)
三、解答题(5小题,每小题10分,共计50分)
1、某校调查学生对“社会主义核心价值观”的内容了解情况,随机抽取部分学生进行问卷调查,问卷共设置“非常了解”、“比较了解”、“一般了解”、“不了解”四个选项,分别记为A、B、C、D,根据调查结果绘制了如图尚不完整的统计图.
“社会主义核心价值观”了解情况条形統计图:
“社会主义核心价值观”了解情况扇形统计图:
请解答下列问题:
(1)本次问卷共随机调查了名学生,扇形统计图在D对应的圆心角为度;
(2)请补全条形统计图;
(3)若该校有1800名学生,试估计该校选择“非常了解”的学生有多少人?
2、为选拔同学参加全市组织的青少年科学知识竞赛,重庆一中在全校进行了“请党放心,强国有我”科学知识竞赛,并对八年级(3)班全体同学本次知识竞赛成绩进行了统计,我们将成绩分为、、、、五类,制成了如下不完整的条形统计图和扇形统计图(如图所示).
请你根据统计图中的信息,解答下列问题:
(1)八年级(3)班学生总人数是__________人;在扇形统计图中,的值是__________;
(2)若八年级(3)班得等级的同学人数是得等级的同学人数的4倍,请将条形统计图补充完整;
(3)若等级为表示优秀,等级为表示良好,等级为表示合格,等级为表示不合格,等级为表示差,根据本次统计结果,估计全校2000名学生中知识竞赛成绩在合格及以上的学生大约有多少人?
3、为了解地铁开通对节约“出行时间”影响情况,对地铁1号线上某趟列车上的部分乘客进行随机抽样调查.将调查结果分为、、、四类,其中表示“出行节约0﹣10分钟”,表示“出行节约10﹣30分钟”,表示“出行节约30分钟以上”,表示“其他情况”,并根据调查结果绘制了图①、图②这两个不完整的统计图表.
(1)求这次调查的总人数.
(2)补全条形统计图.
(3)在图②的扇形统计图中,求类所对应的扇形圆心角的度数.
4、为了了解某地区60~75岁的老年人的锻炼情况,利用公安机关户籍网,随机电话调查了该区60~75岁的300名老人平均每天的锻炼时间,整理得到下面的表格:
平均每天锻炼时间 人数 占被调查数的百分比
男 女 合计
1h以内(含1h) 43 83 126 42%
1-2h(含2h) 20 28 48 16%
2h以上 7 5 12 4%
不参加锻炼 77 37 114 38%
合计 147 153 300 100%
(1)男性老年人参加锻炼的人数有________人,女性老年人参加锻炼的人数有________人,老年人中,参加锻炼的占被调查者的________%;
(2)不参加锻炼的老年人中,男性大约是女性的几倍?
(3)根据此表数据分析,你对该区老年人的锻炼情况有什么建议吗?
(4)对本题的课题进行调查时,如果清晨到公园或市人民广场询问300名老年人,或在某居民小区调查10名老年人,你认为这样得到的数据,可以作为调查分析、得出结论的依据吗?请说明理由.
5、为提升学生的艺术素养,学校计划开设四门艺术选修课:A:书法;B,绘画;C,乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),将数据进行整理,并绘制成如图两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)木次调查的学生共有 人,扇形统计图中∠α的度数是 ;
(2)请把条形统计图补充完整.
---------参考答案-----------
一、单选题
1、C
【解析】
【分析】
经销商最感兴趣的是这组鞋号中销售量最大的尺码,即这组鞋号的众数.
【详解】
解:由于众数是数据中出现次数最多的数.经销商最感兴趣的是这组鞋号中销售量最大的尺码,故应关注众数的大小.
故选:C.
【点睛】
本题主要考查学生对统计量的意义的理解与运用,要求学生对统计量进行合理的选择和恰当的运用.
2、B
【解析】
【分析】
直接根据单项式以及多项式的相关概念,正数和负数,抽样调查和全面调查的概念进行判断即可.
【详解】
解:①a表示一个正数、0或者负数,故原说法不正确;
②若|x|=x,则x为正数或0,故原说法不正确;
③单项式﹣的系数是﹣,故原说法不正确;
④多项式﹣3a2b+7a2b2﹣2ab﹣1的次数是4,故原说法正确;
⑤了解全市中小学生每天的零花钱适合抽样调查,故原说法正确;
⑥调查七年级(1)班学生的某次数学考试成绩适合全面调查,故原说法不正确.
正确的个数为2个,
故选:B.
【点睛】
本题考查了多项式、正数和负数、抽样调查和全面调查及绝对值的性质,掌握它们的性质概念是解本题的关键.
3、A
【解析】
【分析】
根据抽样调查和普查的定义进行求解即可.
【详解】
解:A.调查一批防疫口罩的质量,适合抽样调查,故选项符合题意;
B.调查某校九年级学生的视力,适合全面调查,故选项不符合题意;
C.对乘坐某班次飞机的乘客进行安检,适合全面调查,故选项不符合题意;
D.国务院于2020年11月1日开展的第七次全国人口调查,适合全面调查,故选项不符合题意;
故选A.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4、A
【解析】
【分析】
每组的数据个数就是每组的频数,40减去第1,2,3,5小组数据的个数就是第4组的频数.
【详解】
解:第4小组的频数是40 (6+5+15+7)=7,
故选:A.
【点睛】
本题考查频数和频率的知识,注意掌握每个小组的频数等于数据总数减去其余小组的频数,即各小组频数之和等于数据总和.
5、C
【解析】
【分析】
各组的频数的和就是总人数,再根据百分比、众数、中位数的定义逐一解题.
【详解】
解:A. 该学校教职工总人数是4+6+11+10+9+6+4=50人,正确,故A不符合题意;
B. 年龄在小组的教职工人数占总人数的20%,正确,故B不符合题意;
C. 教职工年龄的中位数在这一组,某教师40岁,则全校恰有10名教职工比他年轻说法是错误的,故C符合题意;
D. 教职工年龄分布最集中的在这一组,正确,故D不符合题意,
故选:C.
【点睛】
本题考查频数分布直方图,是重要考点,从图中获取正确信息是解题关键.
6、B
【解析】
【分析】
总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体.本题考查的对象是七年级800名学生期中数学考试情,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本.
【详解】
解:A、题中的调查方式为抽样调查,选项正确,不符合题意;
B、总体为800名学生的期中数学成绩,而不是学生,选项错误,符合题意;
C、每名学生的期中数学成绩是个体,选项正确,不符合题意;
D、100名学生的期中数学成绩是总体的一个样本,选项正确,不符合题意;
故选B
【点睛】
本题主要考查了总体、个体与样本,解题要分清具体问题中的总体、个体与样本.关键是明确考查的对象,总体、个体与样本的考察对象是相同的,所不同的是范围的大小.
7、A
【解析】
【分析】
根据频数发布直方图,跳绳次数不少于100次的人数相加除总人数后再乘即可得;由频数分布直方图可知,大多数学生跳绳次数在范围内;因为每组数据包括左端值不包括右端值,所以跳绳次数最多的不是次;由样本可以估计全年级人中跳绳次数在次的大约有(人),进行判断即可得.
【详解】
A、跳绳次数不少于次的占,选项说法正确,符合题意;
B、由频数分布直方图可知,大多数学生跳绳次数在范围内,选项说法错误,不符合题意;
C、每组数据包括左端值不包括右端值,故跳绳次数最多的不是次,选项说法错误,不符合题意;
D、由样本可以估计全年级人中跳绳次数在次的大约有(人),选项说法错误,不符合题意;
故选A.
【点睛】
本题考查了频数(率)分布直方图,解题的关键是能够根据频数(率)分布直方图所给的信息进行求解.
8、D
【解析】
【分析】
根据普查和抽样调查的定义进行逐一判断即可.
【详解】
解:A、调查佛山市市民的吸烟情况,应采用抽样调查,故此选项不符合题意;
B、调查佛山市电视台某节目的收视率,应采用抽样调查,故此选项不符合题意;
C、调查佛山市市民家庭日常生活支出情况,应采用抽样调查,故此选项不符合题意;
D、调查佛山市某校某班学生对“文明佛山”的知晓率,应采用普查,故此选项符合题意;
故选D.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
9、C
【解析】
【分析】
根据全面调查与抽样调查的意义,结合具体的问题情境进行判断即可.
【详解】
解:A.了解外地游客对岳飞庙的印象,可采取抽样调查,因此选项A不符合题意;
B.了解一批圆珠笔的寿命,可采取抽样调查,因此选项B不符合题意;
C.了解某班学生的身高情况,可采用全面调查,因此选项C符合题意;
D.了解人们保护海洋的意识,可采取抽样调查,因此选项D不符合题意;
故选:C.
【点睛】
本题考查全面调查与抽样调查,理解全面调查与抽样调查的意义和适用的具体问题情境是正确判断的关键.
10、D
【解析】
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,再逐一分析即可.
【详解】
解:A.了解一批电灯泡的使用寿命,具有破坏性,适合抽样调查,不符合题意;
B.调查榆林市中学生的视力情况,适合抽样调查,不符合题意;
C.了解榆林市居民节约用水的情况,适合抽样调查,不符合题意;
D.调查“天问一号”火星探测器零部件的的质量,必需采用全面调查,符合题意;
故选:D.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
二、填空题
1、全面调查
【解析】
【分析】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
【详解】
解:因为要了解全班同学的视力情况范围较小、难度不大,所以应采取全面调查的方法比较合适.
故答案为:全面调查.
【点睛】
本题考查的是调查方法的选择;正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析.
2、①③④
【解析】
【分析】
对每个选项的问题逐一计算,加以甄别即可.
【详解】
解:本次调查的总人数为(人).
∴①正确;
∵行走步数为8~12千步的人数为70人,而调查的总人数为200人,没有超过一半
∴②错误;
∵行走步数为12~16千步的人数为(人).
∴③选项正确;
行走步数为4~8千步的扇形的圆心角为.
∴④正确.
故答案为:①③④.
【点睛】
本题考查了统计调查等知识点,熟知各种算法是解题的基础,从统计图中提取相关的对应数据是解题的关键.
3、15
【解析】
【分析】
由共摸了100次球,发现有25次摸到红球知摸到红球的概率为0.25,设盒子中白球有个,可得,解之即可.
【详解】
解:设盒子中白球大约有个,
根据题意,得:,
解得,
经检验是分式方程的解,
所以估计盒子中白球大约有15个,
故答案为:15.
【点睛】
本题考查用样本估计总体,从一个总体得到一个包含大量数据的样本,我们很难从一个个数字中直接看出样本所包含的信息,解题的关键是用频率分布直方图来表示相应样本的频率分布,从而去估计总体的分布情况.
4、540
【解析】
【分析】
先求出非常清楚所占的百分比,再乘以该校的总人数,即可得出答案.
【详解】
解:根据题意得:
(人.
答:可以估计其中对《未成年人保护法》非常清楚的学生约有540人.
故答案为:540.
【点睛】
此题考查了用样本估计总体,在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
5、全面调查
【解析】
【分析】
根据全面调查和抽样调查的概念判断即可.
【详解】
解:为了全面的、可靠的得到我国人口信息,
所以国家统计局采取的调查方式是全面调查,
故答案为:全面调查.
【点睛】
本题考查的是全面调查和抽样调查,解题的关键是掌握通过普查可以直接得到较为全面、可靠的信息,但花费的时间较长,耗费大,且一些调查项目并不适合普查.其一,调查者能力有限,不能进行普查,其二,调查过程带有破坏性,其三,有些被调查的对象无法进行普查.
三、解答题
1、(1)60,18;(2)15,补图见解答;(3)450.
【分析】
(1)“B比较了解”的有24人,占调查人数的40%,可求出调查人数,进而求出“D一般了解”所占的百分比,进而计算其相应的圆心角的度数,
(2)求出“A非常了解”的人数,即可补全条形统计图;
(3)用该校的总人数乘以“非常了解”的人数所占的百分比即可.
【详解】
解:(1)本次问卷共随机调查的学生数是:24÷40%=60(名),
扇形统计图中D对应的圆心角为360°×=18°,
故答案为:60,18;
(2)60×25%=15(人),
补全条形统计图如图所示:
(3)1800×=450(人),
答:估计该校选择“非常了解”的学生有450人.
【点睛】
本题考查扇形统计图、条形统计图的意义和制作方法,从两个统计图中获取数量和数量关系是正确解答的关键.
2、(1)50;20;(2)补全条形见祥解;(3)全校2000名学生中知识竞赛成绩在合格及以上的学生大约有1440人.
【分析】
(1)先从条形图统计类人数为12人,从扇形统计图中B类人数所占百分比为24%,再求八年级(3)班学生总人数是12÷24%=50人,再求出D类的百分比即可;
(2)根据C等级的同学人数是得等级的同学人数的4倍,设等级的同学人数为x人,则等级的同学人数为4x人,列出方程x+4x=50-8-12-10,求解即可;
(3)先求出八年级(3)班知识竞赛成绩在合格及以上的学生大有8+12+16=36人,再求出占班级人数的百分比为36÷50×100%=72%,然后利用样本的百分比含量估计全校2000名学生中知识竞赛成绩在合格及以上的学生大约有2000×72%=1440人即可.
【详解】
解:(1)八年级(3)班全体同学本次知识竞赛成绩从条形图统计类人数为12人,从扇形统计图中B类人数所占百分比为24%,
∴八年级(3)班学生总人数是12÷24%=50人
∴10÷50×100%=20%,
∴a=20,
故答案为50;20;
(2)∵等级的同学人数是得等级的同学人数的4倍
设等级的同学人数为x人,则等级的同学人数为4x人,
∴x+4x=50-8-12-10,
∴x=4;
补全条形图如下
(3)八年级(3)班知识竞赛成绩在合格及以上的学生大有8+12+16=36人,占班级人数的百分比为36÷50×100%=72%,
∴全校2000名学生中知识竞赛成绩在合格及以上的学生大约有2000×72%=1440人.
【点睛】
本题考查样本的容量,从条形图与扇形图获取信息,补画条形统计图,用样本的百分比含量估计总体中的数量,掌握样本的容量的求法,从条形图与扇形图获取信息,补画条形统计图,用样本的百分比含量估计总体中的数量是解题关键.
3、(1)50人;(2)见解析;(3)108°
【分析】
(1)利用类的人数除以类所占百分比,即可求解;
(2)求出“出行节约30分钟以上”的人数,即可求解;
(3)用360°乘以类所占的百分比,即可求解.
【详解】
解:(1)调查的总人数是:(人).
(2)“出行节约30分钟以上”的人数有 (人),
补全图形,如图所示:
(3)A类所对应的扇形圆心角的度数是.
【点睛】
本题主要考查了条形统计图和扇形统计图,明确题意,准确获取信息是解题的关键.
4、(1)70,116,62;(2)2倍;(3)要增强该地区老年人“生命在于运动”的观念;(4)不可以,理由见解析
【分析】
(1)观察表格可得出男性老年人和女性老年人参加锻炼的人数,由此进行解答;
(2)由表格可知不参加锻炼的老年人中,其中男性有77人,女性有37人,进而可得到男性人数和女性人数的倍数关系;
(3)此题答案不唯一,根据图表分析参加锻炼的人数不太多,可以就注重锻炼来分析;
(4)可以根据抽样调查中样本的代表性进行解答.
【详解】
解: (1)男性老年人参加锻炼的人数有43+20+7=70(人),女性参加锻炼的人数有83+28+5=116(人);老年人中,参加锻炼的占被调查者的.
(2)不参加锻炼的老年人中,其中男性有77人,女性有37人,故男性大约是女性的2倍.
(3)根据此表数据分析:不参加锻炼的老年人约占38%,可见该地区的老年人锻炼意识不强,尤其是男性老年人,只有半数的男性老年人参加锻炼,所以要增强该地区老年人“生命在于运动”的观念.
(4)不可以,因为,清晨到公园或市民广场的老年人都是注意锻炼的老年人,不能代表该区所有的老年入的锻炼情况,不具有广泛的代表性,即样本不具有代表性、广泛性,故这种调查方法得出的结论不符合实际.
【点睛】
本题考查抽样调查的知识,解题的关键是对表格进行正确分析进而得到答案.
5、(1);(2)画图见解析
【分析】
(1)由B组8人,占比20%,列式可得总人数,由C组的占比乘以可得圆心角的度数;
(2)先计算出C组的人数,再补全图形即可.
【详解】
解:(1)由B组8人,占比20%,可得总人数为:人,
所以C组所在扇形的圆心角为:
故答案为:
(2)C组的人数为:人,
补全图形如下:
【点睛】
本题考查的是从扇形图与条形图中获取信息,频数与频率,画条形统计图,计算扇形某部分的圆心角,掌握以上基础知识是解题的关键.
