6.3.1 平面向量基本定理 同步训练 -2021-2022学年高一下学期数学人教A版(2019)必修第二册(word版含答案)
文档属性
| 名称 | 6.3.1 平面向量基本定理 同步训练 -2021-2022学年高一下学期数学人教A版(2019)必修第二册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 260.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 15:46:58 | ||
图片预览


文档简介
6.3.1 平面向量基本定理(课时训练)
【巩固基础】
1.设e1,e2是平面内两个向量,则有( )
A.e1,e2一定平行
B.e1,e2的模一定相等
C.对于平面内的任一向量a,都有a=λe1+μe2(λ,μ∈R)
D.若e1,e2不共线,则对平面内的任一向量a都有a=λe1+μe2(λ,μ∈R)
2.设向量e1与e2不共线,若3xe1+(10-y)e2=(4y-7)e1+2xe2,则实数x,y的值分别为( )
A.0,0 B.1,1
C.3,0 D.3,4
3.(多选题)已知e1、e2是表示平面内所有向量的一组基底,则下列四个向量中,能作为一组基底的是( )
A.{e1+e2,e1-e2} B.{3e1-2e2,4e2-6e1}
C.{e1+2e2,e2+2e1} D.{e2,e1+e2}
4.在△ABC中,点D在BC边上,且=2,设=a,=b,则可用基底a,b表示为( )
A.(a+b) B.a+b
C.a+b D.(a+b)
5.若D点在△ABC的边BC上,且=4=r+s,则3r+s的值为( )
A. B. C. D.
6.如图,在正方形ABCD中,点E满足=,点F满足=2,那么=( )
A.- B.+
C.- D.+
7.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则( )
A.=-+ B.=-
C.=- D.=-+
8.设e1,e2是平面内一组基向量,且a=e1+2e2,b=-e1+e2,则向量e1+e2可以表示为以a,b为基向量的线性组合,即e1+e2=________
9.若向量a=4e1+2e2与b=ke1+e2共线,其中e1,e2是同一平面内两个不共线的向量,则k的值为________
10.设D,E分别是△ABC的边AB,BC上的点,AD=AB,BE=BC,若=λ1+λ2(λ1,λ2为实数),则λ1+λ2的值为________
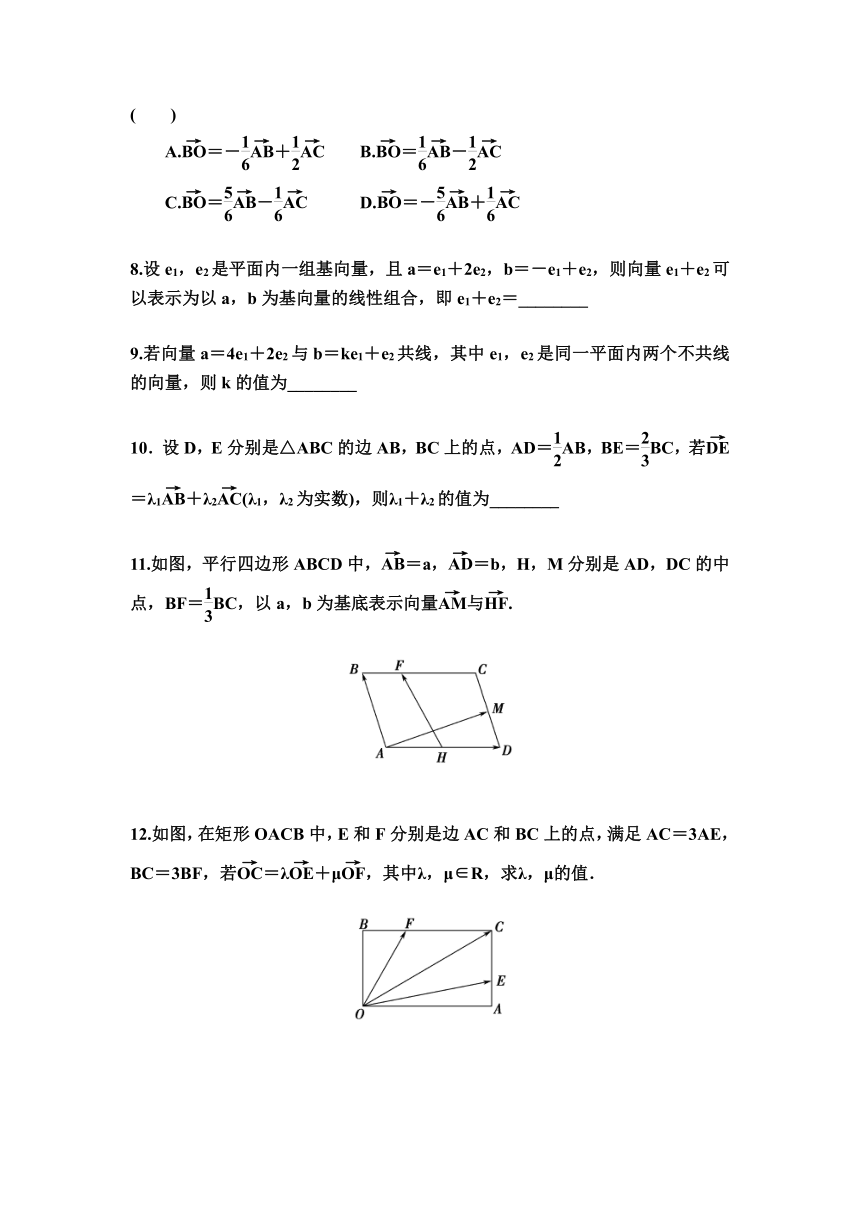
11.如图,平行四边形ABCD中,=a,=b,H,M分别是AD,DC的中点,BF=BC,以a,b为基底表示向量与.
12.如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足AC=3AE,BC=3BF,若=λ+μ,其中λ,μ∈R,求λ,μ的值.
【提升素养】
13.(多选题)若e1,e2是平面α内两个不共线的向量,则下列说法正确的是( )
A.λe1+μe2(λ,μ∈R)可以表示平面α内的所有向量
B.对于平面α中的任一向量a,使a=λe1+μe2的实数λ,μ有无数多对
C.若λ1,μ1,λ2,μ2均为实数,且向量λ1e1+μ1e2与λ2e1+μ2e2共线,则有且只有一个实数λ,使λ1e1+μ1e2=λ(λ2e1+μ2e2)
D.若存在实数λ,μ使λe1+μe2=0,则λ=μ=0
14.已知O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足=+λ(λ∈[0,+∞)),则点P的轨迹一定通过△ABC的( )
A.外心 B.内心
C.重心 D.垂心
15.若点M是△ABC所在平面内一点,且满足:=+.则△ABM与△ABC的面积之比为________
16.如图,平行四边形ABCD的对角线AC,BD交于O点,线段OD上有点M满足=3,线段CO上有点N满足=λ(λ>0),设=a,=b,已知=μa-b,则λ=________,μ=________.
【拓展思维】
17.如图所示,在 ABCD中,=a,=b,BM=BC,AN=AB.
(1)试用向量a,b来表示,;(2)AM交DN于O点,求AO∶OM的值.
参考答案及详细解析:
1.答案:D
解析:由平面向量基本定理知D正确.
2.答案:D
解析:因为e1与e2不共线,所以解方程组得x=3,y=4.
3.答案:ACD
解析:∵4e2-6e1=-2(3e1-2e2),∴3e1-2e2与4e2-6e1共线,∴它们不能作为一组基底,作为基底的两向量一定不共线.A、C、D选项均可.
4.答案:C
解析:因为=2,所以=.所以=+=+=+(-)=+=a+b.
5.答案:C
解析:因为=4=r+s,所以==(-)=r+s.
所以r=,s=-.所以3r+s=-=.
6.答案:C
解析:=++=-++=-+.故选C.
7.答案:D
解析:如图,D为中点,O为靠近A的三等分点,=+=-+=-+×(+)=-++=-+.
8.答案:a-b
解析:由a=e1+2e2①,b=-e1+e2②,由①+②得e2=a+b,代入①可求得e1=a-b,
所以e1+e2=a-b.
9.答案:2
解析:∵向量a与b共线,∴存在实数λ,使得b=λa,即ke1+e2=λ(4e1+2e2)=4λe1+2λe2.
∵e1,e2是同一平面内两个不共线的向量,
∴∴k=2.
10.答案:
解析:如图,由题意知,D为AB的中点,=,
所以=+=+=+(-)=-+,
所以λ1=-,λ2=,所以λ1+λ2=-+=.
11.解:在平行四边形ABCD中,=a,=b,H,M分别是AD,DC的中点,BF=BC,
∴=+=+=+=b+a,=-=+-=a+b-b=a-b.
12.解:在矩形OACB中,=+,
又=λ+μ=λ(+)+μ(+)=λ+μ=+,
所以=1,=1,所以λ=μ=.
13.答案:AD
解析:由平面向量基本定理,可知AD说法正确,B说法不正确.对于C,当λ1=λ2=μ1=μ2=0时,这样的λ有无数个,故C不正确.
14.答案:B
解析:[为上的单位向量,
为上的单位向量,则+的方向为∠BAC的角平分线的方向.又λ∈[0,+∞),
∴λ的方向与+的方向相同.
而=+λ,∴点P在上移动,
∴点P的轨迹一定通过△ABC的内心.
15.答案:1∶4
解析:如图,由=+可知M,B,C三点共线,
令=λ,则=+=+λ=+λ(-)=(1-λ)+λ λ=,
所以=,即△ABM与△ABC面积之比为1∶4.
16.答案:3,
解析:依题意得=b-a,=a+b,且==(a-b)=a-b,
=+==(a+b),
所以=+=b+=a+b,
=+=a+b+=a+b,即=(a+b)=a+b,
由平面向量基本定理,得解得]
17.解:(1)因为AN=AB,所以==a,所以=-=a-b.因为BM=BC,所以===b,所以=+=a+b.
(2)因为A,O,M三点共线,所以∥,
设=λ,则=-=λ-=λ-b=λa+b.
因为D,O,N三点共线,所以∥,存在实数μ使=μ,则λa+b=μ.
由于向量a,b不共线,则解得所以=,=,
所以AO∶OM=3∶11.
【巩固基础】
1.设e1,e2是平面内两个向量,则有( )
A.e1,e2一定平行
B.e1,e2的模一定相等
C.对于平面内的任一向量a,都有a=λe1+μe2(λ,μ∈R)
D.若e1,e2不共线,则对平面内的任一向量a都有a=λe1+μe2(λ,μ∈R)
2.设向量e1与e2不共线,若3xe1+(10-y)e2=(4y-7)e1+2xe2,则实数x,y的值分别为( )
A.0,0 B.1,1
C.3,0 D.3,4
3.(多选题)已知e1、e2是表示平面内所有向量的一组基底,则下列四个向量中,能作为一组基底的是( )
A.{e1+e2,e1-e2} B.{3e1-2e2,4e2-6e1}
C.{e1+2e2,e2+2e1} D.{e2,e1+e2}
4.在△ABC中,点D在BC边上,且=2,设=a,=b,则可用基底a,b表示为( )
A.(a+b) B.a+b
C.a+b D.(a+b)
5.若D点在△ABC的边BC上,且=4=r+s,则3r+s的值为( )
A. B. C. D.
6.如图,在正方形ABCD中,点E满足=,点F满足=2,那么=( )
A.- B.+
C.- D.+
7.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则( )
A.=-+ B.=-
C.=- D.=-+
8.设e1,e2是平面内一组基向量,且a=e1+2e2,b=-e1+e2,则向量e1+e2可以表示为以a,b为基向量的线性组合,即e1+e2=________
9.若向量a=4e1+2e2与b=ke1+e2共线,其中e1,e2是同一平面内两个不共线的向量,则k的值为________
10.设D,E分别是△ABC的边AB,BC上的点,AD=AB,BE=BC,若=λ1+λ2(λ1,λ2为实数),则λ1+λ2的值为________
11.如图,平行四边形ABCD中,=a,=b,H,M分别是AD,DC的中点,BF=BC,以a,b为基底表示向量与.
12.如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足AC=3AE,BC=3BF,若=λ+μ,其中λ,μ∈R,求λ,μ的值.
【提升素养】
13.(多选题)若e1,e2是平面α内两个不共线的向量,则下列说法正确的是( )
A.λe1+μe2(λ,μ∈R)可以表示平面α内的所有向量
B.对于平面α中的任一向量a,使a=λe1+μe2的实数λ,μ有无数多对
C.若λ1,μ1,λ2,μ2均为实数,且向量λ1e1+μ1e2与λ2e1+μ2e2共线,则有且只有一个实数λ,使λ1e1+μ1e2=λ(λ2e1+μ2e2)
D.若存在实数λ,μ使λe1+μe2=0,则λ=μ=0
14.已知O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足=+λ(λ∈[0,+∞)),则点P的轨迹一定通过△ABC的( )
A.外心 B.内心
C.重心 D.垂心
15.若点M是△ABC所在平面内一点,且满足:=+.则△ABM与△ABC的面积之比为________
16.如图,平行四边形ABCD的对角线AC,BD交于O点,线段OD上有点M满足=3,线段CO上有点N满足=λ(λ>0),设=a,=b,已知=μa-b,则λ=________,μ=________.
【拓展思维】
17.如图所示,在 ABCD中,=a,=b,BM=BC,AN=AB.
(1)试用向量a,b来表示,;(2)AM交DN于O点,求AO∶OM的值.
参考答案及详细解析:
1.答案:D
解析:由平面向量基本定理知D正确.
2.答案:D
解析:因为e1与e2不共线,所以解方程组得x=3,y=4.
3.答案:ACD
解析:∵4e2-6e1=-2(3e1-2e2),∴3e1-2e2与4e2-6e1共线,∴它们不能作为一组基底,作为基底的两向量一定不共线.A、C、D选项均可.
4.答案:C
解析:因为=2,所以=.所以=+=+=+(-)=+=a+b.
5.答案:C
解析:因为=4=r+s,所以==(-)=r+s.
所以r=,s=-.所以3r+s=-=.
6.答案:C
解析:=++=-++=-+.故选C.
7.答案:D
解析:如图,D为中点,O为靠近A的三等分点,=+=-+=-+×(+)=-++=-+.
8.答案:a-b
解析:由a=e1+2e2①,b=-e1+e2②,由①+②得e2=a+b,代入①可求得e1=a-b,
所以e1+e2=a-b.
9.答案:2
解析:∵向量a与b共线,∴存在实数λ,使得b=λa,即ke1+e2=λ(4e1+2e2)=4λe1+2λe2.
∵e1,e2是同一平面内两个不共线的向量,
∴∴k=2.
10.答案:
解析:如图,由题意知,D为AB的中点,=,
所以=+=+=+(-)=-+,
所以λ1=-,λ2=,所以λ1+λ2=-+=.
11.解:在平行四边形ABCD中,=a,=b,H,M分别是AD,DC的中点,BF=BC,
∴=+=+=+=b+a,=-=+-=a+b-b=a-b.
12.解:在矩形OACB中,=+,
又=λ+μ=λ(+)+μ(+)=λ+μ=+,
所以=1,=1,所以λ=μ=.
13.答案:AD
解析:由平面向量基本定理,可知AD说法正确,B说法不正确.对于C,当λ1=λ2=μ1=μ2=0时,这样的λ有无数个,故C不正确.
14.答案:B
解析:[为上的单位向量,
为上的单位向量,则+的方向为∠BAC的角平分线的方向.又λ∈[0,+∞),
∴λ的方向与+的方向相同.
而=+λ,∴点P在上移动,
∴点P的轨迹一定通过△ABC的内心.
15.答案:1∶4
解析:如图,由=+可知M,B,C三点共线,
令=λ,则=+=+λ=+λ(-)=(1-λ)+λ λ=,
所以=,即△ABM与△ABC面积之比为1∶4.
16.答案:3,
解析:依题意得=b-a,=a+b,且==(a-b)=a-b,
=+==(a+b),
所以=+=b+=a+b,
=+=a+b+=a+b,即=(a+b)=a+b,
由平面向量基本定理,得解得]
17.解:(1)因为AN=AB,所以==a,所以=-=a-b.因为BM=BC,所以===b,所以=+=a+b.
(2)因为A,O,M三点共线,所以∥,
设=λ,则=-=λ-=λ-b=λa+b.
因为D,O,N三点共线,所以∥,存在实数μ使=μ,则λa+b=μ.
由于向量a,b不共线,则解得所以=,=,
所以AO∶OM=3∶11.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
