苏教版(2019)必修第一册第8章单元检测word版含答案
文档属性
| 名称 | 苏教版(2019)必修第一册第8章单元检测word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 696.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 13:19:01 | ||
图片预览




文档简介
苏教版(2019) 必修第一册 第8章 单元检测
一、单选题
1.对于函数定义域为R,若,则( )
A.方程一定有一个实数解 B.方程一定有两个实数解
C.方程一定无实数解 D.方程可能无实数解
2.5G技术的数学原理之一是著名的香农公式:它表示:在受高斯白噪声干拢的信道中,最大信息传递速率C取决于信道带宽W﹒信道内所传信号的平均功率S,信道内部的高斯噪声功率N的大小.其中叫做信噪比,按照香农公式,在不改变W的情况下,将信噪比卡从1999提升至,使得C大约增加了20%,则入的值约为( )(参考数据lg2≈0.3,103.96≈9120)
A.9121 B.9119 C.9919 D.10999
3.已知函数为定义在上的奇函数,且,则
A. B. C. D.
4.定义在R上的偶函数,满足,,则函数在区间内零点的个数为( )
A.2个 B.4个 C.6个 D.至少4个
5.已知函数的图像是连续不断的,有如下,的对应值表:
1 2 3 4 5 6
15 10 -7 6 -4 -5
则函数在区间上的零点至少有A.2 B.3个 C.4个 D.5个
6.若函数f(x)在[a,b]上连续,且同时满足f(a)·f(b)<0,f(a)·f()>0.则 ( )
A.f(x)在[a,]上有零点
B.f(x)在[,b]上有零点
C.f(x)在[a,]上无零点
D.f(x)在[,b]上无零点
7.华罗庚是上世纪我国伟大的数学家,以华氏命名的数学科研成果有“华氏定理”、“华氏不等式”、“华王方法”等.他除了数学理论研究,还在生产一线大力推广了“优选法”和“统筹法”.“优选法”,是指研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率:每16人为组,把每个人抽取的鼻咽拭子分泌物混合检查,如果为阴性则全部放行;若为阳性,则对该16人再次抽检确认感染者.某组16人中恰有一人感染(鼻咽拭子样本检验将会是阳性),若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组.继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查……以此类推,最终从这16人中认定那名感染者需要经过( )次检测.
A.3 B.4 C.6 D.7
8.如图是某学校高三年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论:
①一班成绩始终高于年级平均水平,整体成绩比较好;
②二班成绩不够稳定,波动程度较大;
③三班成绩虽然多次低于年级平均水平,但在稳步提升.
其中错误的结论的个数为
A.0 B.1 C.2 D.3
二、多选题
9.(多选)在同一平面直角坐标系中,函数与(,且)的图象可能是( )
A. B.
C. D.
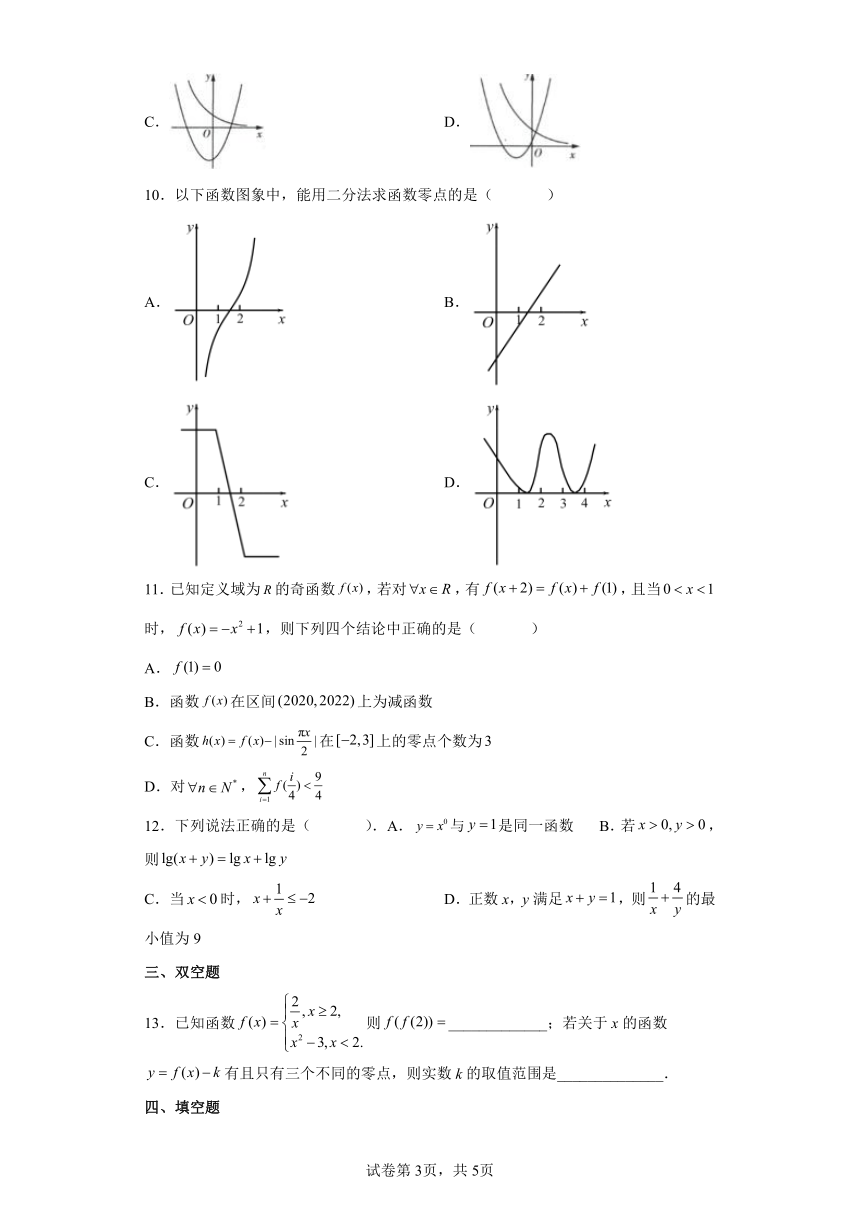
10.以下函数图象中,能用二分法求函数零点的是( )
A. B.
C. D.
11.已知定义域为的奇函数,若对,有,且当时,,则下列四个结论中正确的是( )
A.
B.函数在区间上为减函数
C.函数在上的零点个数为
D.对,
12.下列说法正确的是( ).A.与是同一函数 B.若,则
C.当时, D.正数x,y满足,则的最小值为9
三、双空题
13.已知函数则_____________;若关于x的函数有且只有三个不同的零点,则实数k的取值范围是______________.
四、填空题
14.已知函数f (x)为定义在R上的奇函数,当x>0时,,若关于x的方程在[1,3]上有解,则t的最大值为______.
15.定义在R上的奇函数f(x),当x≥0时,f(x)=,则关于x的函数F(x)=f(x)-的所有零点之和为______.
16.以下是利用二分法求函数f (x) = x3 – 3的一个正实数零点的过程,当精确度为时,该函数的零点为______________________________
端点或中点的横坐标 计算端点或中点的函数值 定区间
a0 = 1,b0 = 2 f(1)= –2,f(2)=5 [1,2]
f (x0) = 0.375>0 [1,1.5]
f (x1) = –1.0469<0 [1.25,1.5]
f (x2) = –0.4004<0 [1.375,1.5]
f (x3) = –0.0295<0 [1.4375,1.5]
f (x4) = 0.1684>0 [1.4375,1.46875]
f (x5)>0 [1.4375,1.453125]
x6 = 1.4453125 f (x6)>0 [1.4375,1.4453125]
五、解答题
17.已知函数,求
(1)函数的定义域;
(2)判断函数的奇偶性.
18.为了做好新冠疫情防控工作,某学校要求全校各班级每天利用课间操时间对各班教室进行药熏消毒.现有一种备选药物,根据测定,教室内每立方米空气中的药含量(单位:mg)随时间(单位:)的变化情况如图所示,在药物释放的过程中与成正比,药物释放完毕后,与的函数关系为(为常数),其图象经过,根据图中提供的信息,解决下面的问题.
(1)求从药物释放开始,与的函数关系式;
(2)据测定,当空气中每立方米的药物含量降低到mg以下时,才能保证对人身无害,若该校课间操时间为分钟,据此判断,学校能否选用这种药物用于教室消毒?请说明理由.
19.已知函数且.
(1)判断函数的奇偶性,并证明;
(2)当时,函数的值城是[-1,1].求实数a的值.
20.已知函数,,将函数图象先向右平移1个单位长度,再向上平移1个单位长度,得到函数的图象.
(1)求函数的解析式;
(2)设函数,若有零点,求实数m的取值范围.
21.已知函数;
(1)为何值时,方程:在上有两解?
(2)若,试求:的最大值.
22.我们知道当时,对一切恒成立,学生小贤在进一步研究指数幂运算时,发现有这么一个等式,带着好奇,他进一步对进行深入研究.
(1)当时,求的值
(2)当时,求证:是不存在的;
(3)求证:只有一对正整数对使得等式成立.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
利用零点存在性定理,即可容易判断.
【详解】
因为,且的定义域为,
若是连续函数,则根据函数的零点存在性定理,
故可得在区间上一定有一个实数解;
若不是连续函数,则在区间上不一定有实数解.
故选:D.
【点睛】
本题考查零点存在性定理,属基础题.
2.B
【解析】
【分析】
根据题意先建立数学模型,然后利用对数求值进行计算.
【详解】
解:由题意得:
,
又
故
故选:B
3.D
【解析】
【分析】
根据函数的周期性可得,再根据奇偶性可得.
【详解】
因为,故为周期函数,
而,所以,故选D.
【点睛】
本题考查函数的周期性和奇函数的性质,属于基础题.
4.D
【解析】
【分析】
由,得到函数为周期为3的函数,利用偶函数得到,然后利用周期性得到均为0.
【详解】
因为,所以函数为周期为3的函数;
又因为为偶函数,,
所以,即,,,
所以函数在区间内零点的个数至少4个.
故选:D
5.B
【解析】
【分析】
根据表格中各点对应的函数值的正负,以及连续函数的零点存在定理,得到答案.
【详解】
由题表可知.
又的图像为连续不断的曲线,
所以在区间,,上各至少有一个零点.
因此上至少有3个零点,
故选项.
【点睛】
本题考查连续函数的零点存在定理,属于简单题.
6.B
【解析】
【详解】
由题函数在 上连续,且同时满足 由“二分法”可知,一定有 ,即函数 在上有零点
故选B
7.B
【解析】
类比二分法,将16人均分为两组,选择其中一组进行检测,再把认定的这组的8人均分两组,选择其中一组进行检测,以此类推,即可得解.
【详解】
先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组,此时进行了1次检测.继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查,为阴性则认定在另一组;若为阳性,则认定在本组,此时进行了2次检测.继续把认定的这组的4人均分两组,选其中一组2人的样本混合检查,为阴性则认定在另一组;若为阳性,则认定在本组,此时进行了3次检测.选认定的这组的2人中一人进行样本混合检查,为阴性则认定是另一个人;若为阳性,则认定为此人,此时进行了4次检测.所以,最终从这16人中认定那名感染者需要经过4次检测.
故选:B.
【点睛】
本题考查的是二分法的实际应用,考查学生的逻辑推理能力,属于基础题.
8.A
【解析】
【分析】
看图分析,①比较一班与年级平均成绩的大小;②看二班的成绩波动;③看三班的平均成绩,以及增减性,即可得到答案.
【详解】
由图可知,一班成绩始终高于年级平均水平,整体成绩比较好,故①正确;
二班的成绩有时高于年级整体成绩,有时低于年级整体成绩,特别是第六次成绩远低于
年级整体成绩,可知二班成绩不稳定,波动程度较大,故②正确;
三班成绩虽然多数时间低于年级平均水平,只有第六次高于年级整体成绩,
但在稳步提升,故③正确.
∴错误结论的个数为0.
故选:A.
【点睛】
本题考查对图象的分析、理解与应用,可从函数值的大小关系,波动情况,增减性等方面分析,属于容易题.
9.AC
【解析】
【分析】
为指数函数,分与两种情况讨论,从而判断出图象的可能结果.
【详解】
若,则函数是R上的增函数,函数的图象的对称轴方程为且,故A符合,B不符合;若,则函数是R上减函数,且当时,,所以函数的图象与y轴的负半轴相交,故C符合,D不符合.
故选:AC.
10.ABC
【解析】
【分析】
根据利用二分法无法求不变号的零点问题确定选项.
【详解】
D选项虽然有零点,但是在零点左右两侧函数值符号都相同,
因此不能用二分法求零点,
而A,B,C选项符合利用二分法求函数零点的条件.
故选:ABC.
【点睛】
本题考查了零点判定定理的应用和二分法求解函数的零点.属于容易题.
11.ABD
【解析】
【分析】
令,计算得,即,代入可得函数的周期为,作出图像,即可判断选项A,B,作出函数的图像,可判断在上的零点个数,判断C 选择,对D选项需要利用函数的周期性代入化简求和即可判断.
【详解】
函数的定义域为,又,令,可得,解得,所以,所以,故函数是周期为的周期函数,画出的图象(如图)可知,函数在区间上为减函数,所以函数在区间上为减函数,A,B正确;由图象可知函数在上的零点个数为,所以C不正确;对,
,即每八项的和为,所以,故D正确.
故选:ABD.
【点睛】
函数零点的求解与判断方法:
(1)直接求零点:令,如果能求出解,则有几个解就有几个零点.
(2)零点存在性定理:利用定理不仅要函数在区间上是连续不断的曲线,且,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点.
(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
12.CD
【解析】
【分析】
对于A,由相同函数的定义判断,对于B,利用对数的运算性质判断,对于CD,利用基本不等式判断即可,
【详解】
A选项,定义域不同,故A错误;
B选项,,故B错误;
C选项,时,,时取等,故C正确;
D选项,,时取等,故D正确,
故选:CD.
13.
【解析】
【分析】
由分段函数解析式,先求,再求,根据分段函数的性质确定函数图象,将问题转化为与有三个不同交点,应用数形结合法求k的取值范围.
【详解】
由题设,,则,
∵在上递减且值域为,在上递增且值域为,在上递减且值域为,
∴的图象如下图示:
由图知:有且只有三个不同的零点,即与有三个不同交点,
∴.
故答案为:,
14.-7
【解析】
根据函数f (x)是奇函数,可求得时,函数的解析式,再,分时,时,求解方程得的值,将问题转化为在[1,3]上有解,根据二次函数的性质可求得t的最大值.
【详解】
解:因为函数f (x)为定义在R上的奇函数,当x>0时,,
所以设时,,所以,
设,当时,需,
又在上单调递减,所以,所以方程无解;
当时,需,又在上单调递减,而当时,成立,
所以当时,方程的解为,
所以要使关于x的方程f (x2+4x+t)=在[1,3]上有解,则需在[1,3]上有解,即在[1,3]上有解,
而在[1,3]上单调递减,所以,所以,
所以t的最大值为,
故答案为:.
【点睛】
本题考查根据函数的奇偶性求函数的解析式,以及二次函数的值域问题,属于中档题.
15.
【解析】
【分析】
根据分段函数的解析式和奇函数的对称性作出函数在上的图象和的图象,利用数形结合的方法求解即可
【详解】
∵当x≥0时,f(x)=;
即x∈时,f(x)=
x∈[1,3]时,f(x)=x-2∈[-1,1];
x∈(3,+∞)时,f(x)=4-x∈(-∞,-1)
画出x≥0时f(x)的图象,
再利用奇函数的对称性,画出x<0时f(x)的图象,如图所示;
则直线,与y=f(x)的图象有5个交点,则方程f(x)-=0共五个实根,
最左边两根之和为-6,最右边两根之和为6,
∵x∈(-1,0)时,-x∈(0,1),∴f(-x)=
又f(-x)=-f(x),
∴f(x)=-=
∴中间的一个根满足
即1-x=,解得x=1-,
∴所有根的和为
故答案为
【点睛】
本题综合考察了函数的性质,图象的运用,函数的零点与函数交点问题,考查了数形结合的能力,属于中档题
16.或
【解析】
利用零点存在定理,即精确度为,判断的零点在,从而得到答案.
【详解】
∵2-1=1>0.01,
f(1) f (x0)<0且1.5-1=0.5>0.01
f (x1) f (x0)<0且1.5-1.25=0.25>0.01,
f (x2) f (x0)<0且1.5-1.375=0.125>0.01,
f (x3) f (x0)<0且1.5-1.4375=0.0625>0.01,
f (x3) f (x4)<0且1.46875-1.4375=0.0525>0.01,
f (x3) f (x5)<0且1.453125-1.4375=0.015625>0.01,
f (x3) f (x6)<0且1.4453125-1.4375=0.0078125<0.01,
∴函数f (x) = x3 – 3=0的一个有根区间为,
又,
∴零点近似解为或
故答案为:或
【点睛】
二分法求零点:
(1)异号零点:(零点存在定理);
(2)精确度:决定循环终止条件及结果的形式.
17.(1) 且;(2)奇函数
【解析】
【分析】
(1)解不等式即得函数的定义域;(2)利用函数的奇偶性的定义判断函数的奇偶性.
【详解】
(1)由题得得 且x,
所以函数的定义域为且.
(2)由(1)得函数的定义域关于原点对称.
,
所以函数是奇函数.
【点睛】
本题主要考查函数的定义域的求法,考查函数的奇偶性的判断,意在考查学生对这些知识的理解掌握水平.
18.(1);
(2)可以,理由见解析.
【解析】
【分析】
(1)将图象上给定点的坐标代入对应的函数解析式计算作答.
(2)利用(1)的结论结合题意,列出不等式求解作答.
(1)
依题意,当时,设,因函数的图象经过点A,即,解得,
又当时,,解得,而图象过点,则,因此,
所以与的函数关系式是.
(2)
由(1)知,因药物释放完毕后有,,
则当空气中每立方米的药物含量降低到mg以下,有,解得:,
因此至少需要36分钟后才能保证对人身无害,而课间操时间为分钟,
所以学校可以选用这种药物用于教室消毒.
【点睛】
思路点睛:涉及实际应用问题,在理解题意的基础上,找出分散的数量关系,联想与题意有
关的数学知识和方法,将实际问题转化、抽象为数学问题作答.
19.(1)函数为奇函数,证明见解析
(2)3或
【解析】
【分析】
(1)以奇函数定义证明函数为奇函数即可解决;
(2)按底数a分类讨论,依据对数函数的单调性分别去求实数a的值即可解决.
(1)
函数为奇函数,证明如下:
由,解得,则函数定义域为
故函数为奇函数
(2)
令
由得,,,,即
当时,在上单调递减,值城是[-1,1]
则,解之得
当时,在上单调递增,值城是[-1,1]
则,解之得
综上,实数a的值为3或
20.(1),;(2).
【解析】
【分析】
(1)利用平移变换逐步得到函数的解析式即可;
(2)先求解函数解析式和定义域,使方程在定义域内有解,再换元使有解,利用单调性求得对勾函数的值域,即得的取值范围,即解得实数m的取值范围.
【详解】
解:(1)函数,,
将函数图象先向右平移1个单位长度,得到函数,,再向上平移1个单位长度,得到函数,.
所以函数的解析式为,;
(2),由得定义域为,
由有零点,则在上有解,
令,则,即在上有解,
即在上有解,而对勾函数在上单调递增,故,故,即,
所以实数m的取值范围为.
【点睛】
思路点睛:
对于对数函数的复合型函数的性质研究问题,通常采用换元法转化成其他常用函数来研究.
21.(1)或;(2)当时,;当时,.
【解析】
(1)先把原式转化为在上有两解,再用换元法令,可得到在的解的情况可结合两函数图像的交点情况讨论;(2)先化简,再令,,转化为关于的二次函数,从而可求最大值.
【详解】
解:(1),
可化为:在上有两解,
令,
则:在的解如下:
①当时只有一个解或相等解时,有俩解,
即:或,
所以:或;
②当时,有唯一解,;
③当时,有唯一解,;
故或;
(2)由,
得,
令,,
则,
原式转化为:,,
即:,
当时,;
当时,.
综上:当时,;
当时,.
【点睛】
关键点睛:本题主要考查了函数的性质与应用问题.解题时利用换元法,把三角函数化为研究普通函数在某一区间上的性质问题是解决本题的关键.
22.(1);(2)证明见解析;(3)证明见解析.
【解析】
【分析】
(1)当时,,整理后将指数式化为对数式即可求解;
(2)由题意求得的表达式,令,然后分类和讨论即可求证;
(3)将,分离到等式的两侧,然后讨论左右两侧的值即可证得题中的结论.
【详解】
(1)当时,,即,所以,
(2)设,因为,所以,且,
当时,,不成立;
当时,,由可得,
因为,,,所以不成立,
综上所述:当时,是不存在的;
(3)由可得,
当,均为正整数时,等号左侧为的指数幂,故右侧也是的指数幂,
所以,即时符合题意,此时,
所以只有一对正整数对使得等式成立.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.对于函数定义域为R,若,则( )
A.方程一定有一个实数解 B.方程一定有两个实数解
C.方程一定无实数解 D.方程可能无实数解
2.5G技术的数学原理之一是著名的香农公式:它表示:在受高斯白噪声干拢的信道中,最大信息传递速率C取决于信道带宽W﹒信道内所传信号的平均功率S,信道内部的高斯噪声功率N的大小.其中叫做信噪比,按照香农公式,在不改变W的情况下,将信噪比卡从1999提升至,使得C大约增加了20%,则入的值约为( )(参考数据lg2≈0.3,103.96≈9120)
A.9121 B.9119 C.9919 D.10999
3.已知函数为定义在上的奇函数,且,则
A. B. C. D.
4.定义在R上的偶函数,满足,,则函数在区间内零点的个数为( )
A.2个 B.4个 C.6个 D.至少4个
5.已知函数的图像是连续不断的,有如下,的对应值表:
1 2 3 4 5 6
15 10 -7 6 -4 -5
则函数在区间上的零点至少有A.2 B.3个 C.4个 D.5个
6.若函数f(x)在[a,b]上连续,且同时满足f(a)·f(b)<0,f(a)·f()>0.则 ( )
A.f(x)在[a,]上有零点
B.f(x)在[,b]上有零点
C.f(x)在[a,]上无零点
D.f(x)在[,b]上无零点
7.华罗庚是上世纪我国伟大的数学家,以华氏命名的数学科研成果有“华氏定理”、“华氏不等式”、“华王方法”等.他除了数学理论研究,还在生产一线大力推广了“优选法”和“统筹法”.“优选法”,是指研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率:每16人为组,把每个人抽取的鼻咽拭子分泌物混合检查,如果为阴性则全部放行;若为阳性,则对该16人再次抽检确认感染者.某组16人中恰有一人感染(鼻咽拭子样本检验将会是阳性),若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组.继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查……以此类推,最终从这16人中认定那名感染者需要经过( )次检测.
A.3 B.4 C.6 D.7
8.如图是某学校高三年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论:
①一班成绩始终高于年级平均水平,整体成绩比较好;
②二班成绩不够稳定,波动程度较大;
③三班成绩虽然多次低于年级平均水平,但在稳步提升.
其中错误的结论的个数为
A.0 B.1 C.2 D.3
二、多选题
9.(多选)在同一平面直角坐标系中,函数与(,且)的图象可能是( )
A. B.
C. D.
10.以下函数图象中,能用二分法求函数零点的是( )
A. B.
C. D.
11.已知定义域为的奇函数,若对,有,且当时,,则下列四个结论中正确的是( )
A.
B.函数在区间上为减函数
C.函数在上的零点个数为
D.对,
12.下列说法正确的是( ).A.与是同一函数 B.若,则
C.当时, D.正数x,y满足,则的最小值为9
三、双空题
13.已知函数则_____________;若关于x的函数有且只有三个不同的零点,则实数k的取值范围是______________.
四、填空题
14.已知函数f (x)为定义在R上的奇函数,当x>0时,,若关于x的方程在[1,3]上有解,则t的最大值为______.
15.定义在R上的奇函数f(x),当x≥0时,f(x)=,则关于x的函数F(x)=f(x)-的所有零点之和为______.
16.以下是利用二分法求函数f (x) = x3 – 3的一个正实数零点的过程,当精确度为时,该函数的零点为______________________________
端点或中点的横坐标 计算端点或中点的函数值 定区间
a0 = 1,b0 = 2 f(1)= –2,f(2)=5 [1,2]
f (x0) = 0.375>0 [1,1.5]
f (x1) = –1.0469<0 [1.25,1.5]
f (x2) = –0.4004<0 [1.375,1.5]
f (x3) = –0.0295<0 [1.4375,1.5]
f (x4) = 0.1684>0 [1.4375,1.46875]
f (x5)>0 [1.4375,1.453125]
x6 = 1.4453125 f (x6)>0 [1.4375,1.4453125]
五、解答题
17.已知函数,求
(1)函数的定义域;
(2)判断函数的奇偶性.
18.为了做好新冠疫情防控工作,某学校要求全校各班级每天利用课间操时间对各班教室进行药熏消毒.现有一种备选药物,根据测定,教室内每立方米空气中的药含量(单位:mg)随时间(单位:)的变化情况如图所示,在药物释放的过程中与成正比,药物释放完毕后,与的函数关系为(为常数),其图象经过,根据图中提供的信息,解决下面的问题.
(1)求从药物释放开始,与的函数关系式;
(2)据测定,当空气中每立方米的药物含量降低到mg以下时,才能保证对人身无害,若该校课间操时间为分钟,据此判断,学校能否选用这种药物用于教室消毒?请说明理由.
19.已知函数且.
(1)判断函数的奇偶性,并证明;
(2)当时,函数的值城是[-1,1].求实数a的值.
20.已知函数,,将函数图象先向右平移1个单位长度,再向上平移1个单位长度,得到函数的图象.
(1)求函数的解析式;
(2)设函数,若有零点,求实数m的取值范围.
21.已知函数;
(1)为何值时,方程:在上有两解?
(2)若,试求:的最大值.
22.我们知道当时,对一切恒成立,学生小贤在进一步研究指数幂运算时,发现有这么一个等式,带着好奇,他进一步对进行深入研究.
(1)当时,求的值
(2)当时,求证:是不存在的;
(3)求证:只有一对正整数对使得等式成立.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
利用零点存在性定理,即可容易判断.
【详解】
因为,且的定义域为,
若是连续函数,则根据函数的零点存在性定理,
故可得在区间上一定有一个实数解;
若不是连续函数,则在区间上不一定有实数解.
故选:D.
【点睛】
本题考查零点存在性定理,属基础题.
2.B
【解析】
【分析】
根据题意先建立数学模型,然后利用对数求值进行计算.
【详解】
解:由题意得:
,
又
故
故选:B
3.D
【解析】
【分析】
根据函数的周期性可得,再根据奇偶性可得.
【详解】
因为,故为周期函数,
而,所以,故选D.
【点睛】
本题考查函数的周期性和奇函数的性质,属于基础题.
4.D
【解析】
【分析】
由,得到函数为周期为3的函数,利用偶函数得到,然后利用周期性得到均为0.
【详解】
因为,所以函数为周期为3的函数;
又因为为偶函数,,
所以,即,,,
所以函数在区间内零点的个数至少4个.
故选:D
5.B
【解析】
【分析】
根据表格中各点对应的函数值的正负,以及连续函数的零点存在定理,得到答案.
【详解】
由题表可知.
又的图像为连续不断的曲线,
所以在区间,,上各至少有一个零点.
因此上至少有3个零点,
故选项.
【点睛】
本题考查连续函数的零点存在定理,属于简单题.
6.B
【解析】
【详解】
由题函数在 上连续,且同时满足 由“二分法”可知,一定有 ,即函数 在上有零点
故选B
7.B
【解析】
类比二分法,将16人均分为两组,选择其中一组进行检测,再把认定的这组的8人均分两组,选择其中一组进行检测,以此类推,即可得解.
【详解】
先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组,此时进行了1次检测.继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查,为阴性则认定在另一组;若为阳性,则认定在本组,此时进行了2次检测.继续把认定的这组的4人均分两组,选其中一组2人的样本混合检查,为阴性则认定在另一组;若为阳性,则认定在本组,此时进行了3次检测.选认定的这组的2人中一人进行样本混合检查,为阴性则认定是另一个人;若为阳性,则认定为此人,此时进行了4次检测.所以,最终从这16人中认定那名感染者需要经过4次检测.
故选:B.
【点睛】
本题考查的是二分法的实际应用,考查学生的逻辑推理能力,属于基础题.
8.A
【解析】
【分析】
看图分析,①比较一班与年级平均成绩的大小;②看二班的成绩波动;③看三班的平均成绩,以及增减性,即可得到答案.
【详解】
由图可知,一班成绩始终高于年级平均水平,整体成绩比较好,故①正确;
二班的成绩有时高于年级整体成绩,有时低于年级整体成绩,特别是第六次成绩远低于
年级整体成绩,可知二班成绩不稳定,波动程度较大,故②正确;
三班成绩虽然多数时间低于年级平均水平,只有第六次高于年级整体成绩,
但在稳步提升,故③正确.
∴错误结论的个数为0.
故选:A.
【点睛】
本题考查对图象的分析、理解与应用,可从函数值的大小关系,波动情况,增减性等方面分析,属于容易题.
9.AC
【解析】
【分析】
为指数函数,分与两种情况讨论,从而判断出图象的可能结果.
【详解】
若,则函数是R上的增函数,函数的图象的对称轴方程为且,故A符合,B不符合;若,则函数是R上减函数,且当时,,所以函数的图象与y轴的负半轴相交,故C符合,D不符合.
故选:AC.
10.ABC
【解析】
【分析】
根据利用二分法无法求不变号的零点问题确定选项.
【详解】
D选项虽然有零点,但是在零点左右两侧函数值符号都相同,
因此不能用二分法求零点,
而A,B,C选项符合利用二分法求函数零点的条件.
故选:ABC.
【点睛】
本题考查了零点判定定理的应用和二分法求解函数的零点.属于容易题.
11.ABD
【解析】
【分析】
令,计算得,即,代入可得函数的周期为,作出图像,即可判断选项A,B,作出函数的图像,可判断在上的零点个数,判断C 选择,对D选项需要利用函数的周期性代入化简求和即可判断.
【详解】
函数的定义域为,又,令,可得,解得,所以,所以,故函数是周期为的周期函数,画出的图象(如图)可知,函数在区间上为减函数,所以函数在区间上为减函数,A,B正确;由图象可知函数在上的零点个数为,所以C不正确;对,
,即每八项的和为,所以,故D正确.
故选:ABD.
【点睛】
函数零点的求解与判断方法:
(1)直接求零点:令,如果能求出解,则有几个解就有几个零点.
(2)零点存在性定理:利用定理不仅要函数在区间上是连续不断的曲线,且,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点.
(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
12.CD
【解析】
【分析】
对于A,由相同函数的定义判断,对于B,利用对数的运算性质判断,对于CD,利用基本不等式判断即可,
【详解】
A选项,定义域不同,故A错误;
B选项,,故B错误;
C选项,时,,时取等,故C正确;
D选项,,时取等,故D正确,
故选:CD.
13.
【解析】
【分析】
由分段函数解析式,先求,再求,根据分段函数的性质确定函数图象,将问题转化为与有三个不同交点,应用数形结合法求k的取值范围.
【详解】
由题设,,则,
∵在上递减且值域为,在上递增且值域为,在上递减且值域为,
∴的图象如下图示:
由图知:有且只有三个不同的零点,即与有三个不同交点,
∴.
故答案为:,
14.-7
【解析】
根据函数f (x)是奇函数,可求得时,函数的解析式,再,分时,时,求解方程得的值,将问题转化为在[1,3]上有解,根据二次函数的性质可求得t的最大值.
【详解】
解:因为函数f (x)为定义在R上的奇函数,当x>0时,,
所以设时,,所以,
设,当时,需,
又在上单调递减,所以,所以方程无解;
当时,需,又在上单调递减,而当时,成立,
所以当时,方程的解为,
所以要使关于x的方程f (x2+4x+t)=在[1,3]上有解,则需在[1,3]上有解,即在[1,3]上有解,
而在[1,3]上单调递减,所以,所以,
所以t的最大值为,
故答案为:.
【点睛】
本题考查根据函数的奇偶性求函数的解析式,以及二次函数的值域问题,属于中档题.
15.
【解析】
【分析】
根据分段函数的解析式和奇函数的对称性作出函数在上的图象和的图象,利用数形结合的方法求解即可
【详解】
∵当x≥0时,f(x)=;
即x∈时,f(x)=
x∈[1,3]时,f(x)=x-2∈[-1,1];
x∈(3,+∞)时,f(x)=4-x∈(-∞,-1)
画出x≥0时f(x)的图象,
再利用奇函数的对称性,画出x<0时f(x)的图象,如图所示;
则直线,与y=f(x)的图象有5个交点,则方程f(x)-=0共五个实根,
最左边两根之和为-6,最右边两根之和为6,
∵x∈(-1,0)时,-x∈(0,1),∴f(-x)=
又f(-x)=-f(x),
∴f(x)=-=
∴中间的一个根满足
即1-x=,解得x=1-,
∴所有根的和为
故答案为
【点睛】
本题综合考察了函数的性质,图象的运用,函数的零点与函数交点问题,考查了数形结合的能力,属于中档题
16.或
【解析】
利用零点存在定理,即精确度为,判断的零点在,从而得到答案.
【详解】
∵2-1=1>0.01,
f(1) f (x0)<0且1.5-1=0.5>0.01
f (x1) f (x0)<0且1.5-1.25=0.25>0.01,
f (x2) f (x0)<0且1.5-1.375=0.125>0.01,
f (x3) f (x0)<0且1.5-1.4375=0.0625>0.01,
f (x3) f (x4)<0且1.46875-1.4375=0.0525>0.01,
f (x3) f (x5)<0且1.453125-1.4375=0.015625>0.01,
f (x3) f (x6)<0且1.4453125-1.4375=0.0078125<0.01,
∴函数f (x) = x3 – 3=0的一个有根区间为,
又,
∴零点近似解为或
故答案为:或
【点睛】
二分法求零点:
(1)异号零点:(零点存在定理);
(2)精确度:决定循环终止条件及结果的形式.
17.(1) 且;(2)奇函数
【解析】
【分析】
(1)解不等式即得函数的定义域;(2)利用函数的奇偶性的定义判断函数的奇偶性.
【详解】
(1)由题得得 且x,
所以函数的定义域为且.
(2)由(1)得函数的定义域关于原点对称.
,
所以函数是奇函数.
【点睛】
本题主要考查函数的定义域的求法,考查函数的奇偶性的判断,意在考查学生对这些知识的理解掌握水平.
18.(1);
(2)可以,理由见解析.
【解析】
【分析】
(1)将图象上给定点的坐标代入对应的函数解析式计算作答.
(2)利用(1)的结论结合题意,列出不等式求解作答.
(1)
依题意,当时,设,因函数的图象经过点A,即,解得,
又当时,,解得,而图象过点,则,因此,
所以与的函数关系式是.
(2)
由(1)知,因药物释放完毕后有,,
则当空气中每立方米的药物含量降低到mg以下,有,解得:,
因此至少需要36分钟后才能保证对人身无害,而课间操时间为分钟,
所以学校可以选用这种药物用于教室消毒.
【点睛】
思路点睛:涉及实际应用问题,在理解题意的基础上,找出分散的数量关系,联想与题意有
关的数学知识和方法,将实际问题转化、抽象为数学问题作答.
19.(1)函数为奇函数,证明见解析
(2)3或
【解析】
【分析】
(1)以奇函数定义证明函数为奇函数即可解决;
(2)按底数a分类讨论,依据对数函数的单调性分别去求实数a的值即可解决.
(1)
函数为奇函数,证明如下:
由,解得,则函数定义域为
故函数为奇函数
(2)
令
由得,,,,即
当时,在上单调递减,值城是[-1,1]
则,解之得
当时,在上单调递增,值城是[-1,1]
则,解之得
综上,实数a的值为3或
20.(1),;(2).
【解析】
【分析】
(1)利用平移变换逐步得到函数的解析式即可;
(2)先求解函数解析式和定义域,使方程在定义域内有解,再换元使有解,利用单调性求得对勾函数的值域,即得的取值范围,即解得实数m的取值范围.
【详解】
解:(1)函数,,
将函数图象先向右平移1个单位长度,得到函数,,再向上平移1个单位长度,得到函数,.
所以函数的解析式为,;
(2),由得定义域为,
由有零点,则在上有解,
令,则,即在上有解,
即在上有解,而对勾函数在上单调递增,故,故,即,
所以实数m的取值范围为.
【点睛】
思路点睛:
对于对数函数的复合型函数的性质研究问题,通常采用换元法转化成其他常用函数来研究.
21.(1)或;(2)当时,;当时,.
【解析】
(1)先把原式转化为在上有两解,再用换元法令,可得到在的解的情况可结合两函数图像的交点情况讨论;(2)先化简,再令,,转化为关于的二次函数,从而可求最大值.
【详解】
解:(1),
可化为:在上有两解,
令,
则:在的解如下:
①当时只有一个解或相等解时,有俩解,
即:或,
所以:或;
②当时,有唯一解,;
③当时,有唯一解,;
故或;
(2)由,
得,
令,,
则,
原式转化为:,,
即:,
当时,;
当时,.
综上:当时,;
当时,.
【点睛】
关键点睛:本题主要考查了函数的性质与应用问题.解题时利用换元法,把三角函数化为研究普通函数在某一区间上的性质问题是解决本题的关键.
22.(1);(2)证明见解析;(3)证明见解析.
【解析】
【分析】
(1)当时,,整理后将指数式化为对数式即可求解;
(2)由题意求得的表达式,令,然后分类和讨论即可求证;
(3)将,分离到等式的两侧,然后讨论左右两侧的值即可证得题中的结论.
【详解】
(1)当时,,即,所以,
(2)设,因为,所以,且,
当时,,不成立;
当时,,由可得,
因为,,,所以不成立,
综上所述:当时,是不存在的;
(3)由可得,
当,均为正整数时,等号左侧为的指数幂,故右侧也是的指数幂,
所以,即时符合题意,此时,
所以只有一对正整数对使得等式成立.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
