2021—2022学年北师大版数学七年级下册5.3简单的轴对称图形 课件(共21张PPT)
文档属性
| 名称 | 2021—2022学年北师大版数学七年级下册5.3简单的轴对称图形 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
5.3 简单的轴对称图形
学习目标
1.经历探索简单图形的轴对称的过程,进一步理解轴对称的性质,积累数学活动经验,发展空间观念.
2.探索并了解等腰三角形的对称性及其相关性质.
新课导入
轴对称有哪些性质?
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
还记得等腰三角形吗?
有两边相等的三角形叫做等腰三角形.
合作探究
动手做一做:将长方形纸片对折然后沿对角线折叠,在沿折痕剪开,沿直角边展开,得到的三角形有什么特点?
两边相等,两个底角相等
=
=
等腰三角形
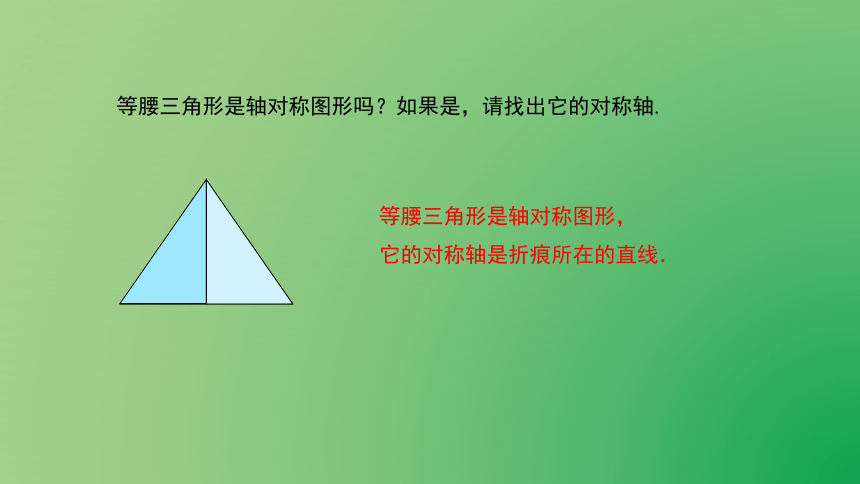
等腰三角形是轴对称图形吗?如果是,请找出它的对称轴.
等腰三角形是轴对称图形,
它的对称轴是折痕所在的直线.
等腰三角形顶角平分线所在的直线是它的对称轴吗?
因为AD是△ABC的角平分线,
所以∠BAD=∠CAD.
等腰三角形顶角平分线所在的直线是它的对称轴.
A
B
C
D
A
B
C
D
等腰三角形底边的中线所在的直线是它的对称轴吗?
因为AD是△ABC的中线,
所以BD=CD.
底边的中线所在的直线是它的对称轴.
=
=
A
B
C
D
等腰三角形底边的高所在的直线是它的对称轴吗?
因为AD是△ABC的高,
所以∠BDA=∠CDA=90°.
底边的高所在的直线是它的对称轴.
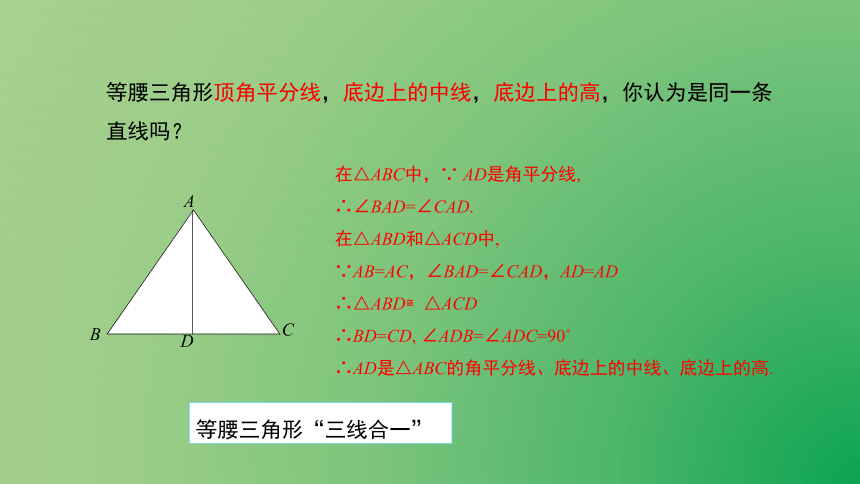
等腰三角形顶角平分线,底边上的中线,底边上的高,你认为是同一条直线吗?
在△ABC中,∵ AD是角平分线,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∵AB=AC,∠BAD=∠CAD,AD=AD
∴△ABD≌△ACD
∴BD=CD, ∠ADB=∠ADC=90
∴AD是△ABC的角平分线、底边上的中线、底边上的高.
A
B
C
D
等腰三角形“三线合一”
等腰三角形的性质
1.等腰三角形是轴对称图形.
3.等腰三角形的两个底角相等.
2.等腰三角形的顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
三边都相等的三角形是等边三角形也叫正三角形
(1)等边三角形是轴对称图形吗?找出对称轴
(2)你能发现它的哪些特征?
等边三角形每条边上的中线、高线和对角的平分线互相重合.
等边三角形的三个内角都相等,且每个内角都是60°.
等边三角形的性质
等边三角形的三个内角都相等,且每个内角都是60°.
等边三角形每条边上的中线、高线和对角的平分线互相重合.
等边三角形有三条对称轴.
例1、等腰三角形的一个角是70°,则它的顶角的度数是( )
A.70° B.20°
C.70°或20° D.70°或40°
D
例2、如图,在△ABC中,AB=AC,M是边BC的中点,BD平分∠ABC,交AM于点E,交AC于点D,若∠AED=64°,求∠BAC的度数.
解: ∵AB=AC,M是边BC的中点,
∴∠AMB=90°,
∠BAM=∠CAM.
∵∠BEM=∠AED=64°,
∴∠EBM=26°.
∵BD平分∠ABC,
∴∠ABC=2∠EBM=52°,
∴∠BAM=90°-∠ABM=38°,
∴∠BAC=∠BAM+∠CAM=2∠BAM=76°.
例3、如图,在等腰三角形ABC中,AB=AC,O是BC的中点,OD⊥AB于点D,OE⊥AC于点E.试说明:AD=AE.
证明:连接AO,
∵AB=AC,O是BC的中点,
∴AO平分∠BAC,
∴∠DAO=∠EAO.
∵OD⊥AB,OE⊥AC,
∴∠ADO=∠AEO=90°.
在△AOD和△AOE中,
∴△AOD≌△AOE(AAS),∴AD=AE.
随堂练习
1.下列不是轴对称图形的是 ( )
A.有两个角相等的三角形
B.有一个角为45°的直角三角形
C.有一个角为30°,另一个角为120°的三角形
D.有一个内角为30°的直角三角形
D
2.等腰三角形的一个内角为70°,则另外两个内角的度数分别是 ( )
A.55°,55°
B.70°,40°或70°, 55°
C.70°,40°
D.55°, 55°或70°, 40°
D
3.如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是 ( )
A.40° B.35° C.25° D.20°
C
4.如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM+CN=9,则线段MN的长为( )
A.6 B.7 C.8 D.9
D
5.如图,BO,CO分别是∠ABC,∠ACB的平分线,它们相交于点O,若∠ABC=50°,∠ACB=60°,试求∠BOC的度数.
解:∵BO平分∠ABC,CO平分∠ACB,
∠ABC=50°,∠ACB=60°,
∴∠ABO=∠OBC=∠ABC=25°,
∠ACO=∠OCB=∠ACB=30°,
在△BOC中,∠BOC=180°-∠OBC-∠OCB=125°.
6.如图所示,已知△ABC和△BDE都是等边三角形,试说明AE=CD.
解:∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
在△ABE和△CBD中,
∴△ABE≌△CBD(SAS),
∴AE=CD.
课堂小结
等腰三角形
等边对等角
三线合一
等边三角形
每个内角都为60°
三条对称轴
三线合一
5.3 简单的轴对称图形
学习目标
1.经历探索简单图形的轴对称的过程,进一步理解轴对称的性质,积累数学活动经验,发展空间观念.
2.探索并了解等腰三角形的对称性及其相关性质.
新课导入
轴对称有哪些性质?
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
还记得等腰三角形吗?
有两边相等的三角形叫做等腰三角形.
合作探究
动手做一做:将长方形纸片对折然后沿对角线折叠,在沿折痕剪开,沿直角边展开,得到的三角形有什么特点?
两边相等,两个底角相等
=
=
等腰三角形
等腰三角形是轴对称图形吗?如果是,请找出它的对称轴.
等腰三角形是轴对称图形,
它的对称轴是折痕所在的直线.
等腰三角形顶角平分线所在的直线是它的对称轴吗?
因为AD是△ABC的角平分线,
所以∠BAD=∠CAD.
等腰三角形顶角平分线所在的直线是它的对称轴.
A
B
C
D
A
B
C
D
等腰三角形底边的中线所在的直线是它的对称轴吗?
因为AD是△ABC的中线,
所以BD=CD.
底边的中线所在的直线是它的对称轴.
=
=
A
B
C
D
等腰三角形底边的高所在的直线是它的对称轴吗?
因为AD是△ABC的高,
所以∠BDA=∠CDA=90°.
底边的高所在的直线是它的对称轴.
等腰三角形顶角平分线,底边上的中线,底边上的高,你认为是同一条直线吗?
在△ABC中,∵ AD是角平分线,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∵AB=AC,∠BAD=∠CAD,AD=AD
∴△ABD≌△ACD
∴BD=CD, ∠ADB=∠ADC=90
∴AD是△ABC的角平分线、底边上的中线、底边上的高.
A
B
C
D
等腰三角形“三线合一”
等腰三角形的性质
1.等腰三角形是轴对称图形.
3.等腰三角形的两个底角相等.
2.等腰三角形的顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
三边都相等的三角形是等边三角形也叫正三角形
(1)等边三角形是轴对称图形吗?找出对称轴
(2)你能发现它的哪些特征?
等边三角形每条边上的中线、高线和对角的平分线互相重合.
等边三角形的三个内角都相等,且每个内角都是60°.
等边三角形的性质
等边三角形的三个内角都相等,且每个内角都是60°.
等边三角形每条边上的中线、高线和对角的平分线互相重合.
等边三角形有三条对称轴.
例1、等腰三角形的一个角是70°,则它的顶角的度数是( )
A.70° B.20°
C.70°或20° D.70°或40°
D
例2、如图,在△ABC中,AB=AC,M是边BC的中点,BD平分∠ABC,交AM于点E,交AC于点D,若∠AED=64°,求∠BAC的度数.
解: ∵AB=AC,M是边BC的中点,
∴∠AMB=90°,
∠BAM=∠CAM.
∵∠BEM=∠AED=64°,
∴∠EBM=26°.
∵BD平分∠ABC,
∴∠ABC=2∠EBM=52°,
∴∠BAM=90°-∠ABM=38°,
∴∠BAC=∠BAM+∠CAM=2∠BAM=76°.
例3、如图,在等腰三角形ABC中,AB=AC,O是BC的中点,OD⊥AB于点D,OE⊥AC于点E.试说明:AD=AE.
证明:连接AO,
∵AB=AC,O是BC的中点,
∴AO平分∠BAC,
∴∠DAO=∠EAO.
∵OD⊥AB,OE⊥AC,
∴∠ADO=∠AEO=90°.
在△AOD和△AOE中,
∴△AOD≌△AOE(AAS),∴AD=AE.
随堂练习
1.下列不是轴对称图形的是 ( )
A.有两个角相等的三角形
B.有一个角为45°的直角三角形
C.有一个角为30°,另一个角为120°的三角形
D.有一个内角为30°的直角三角形
D
2.等腰三角形的一个内角为70°,则另外两个内角的度数分别是 ( )
A.55°,55°
B.70°,40°或70°, 55°
C.70°,40°
D.55°, 55°或70°, 40°
D
3.如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是 ( )
A.40° B.35° C.25° D.20°
C
4.如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM+CN=9,则线段MN的长为( )
A.6 B.7 C.8 D.9
D
5.如图,BO,CO分别是∠ABC,∠ACB的平分线,它们相交于点O,若∠ABC=50°,∠ACB=60°,试求∠BOC的度数.
解:∵BO平分∠ABC,CO平分∠ACB,
∠ABC=50°,∠ACB=60°,
∴∠ABO=∠OBC=∠ABC=25°,
∠ACO=∠OCB=∠ACB=30°,
在△BOC中,∠BOC=180°-∠OBC-∠OCB=125°.
6.如图所示,已知△ABC和△BDE都是等边三角形,试说明AE=CD.
解:∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
在△ABE和△CBD中,
∴△ABE≌△CBD(SAS),
∴AE=CD.
课堂小结
等腰三角形
等边对等角
三线合一
等边三角形
每个内角都为60°
三条对称轴
三线合一
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
